分数阶全息的转子起停车故障特征提取方法

2016-12-07杜小伟温广瑞廖与禾

振动、测试与诊断 2016年4期

关键词：倍频傅里叶全息

杜小伟，温广瑞,2，江铖，廖与禾

(1.西安交通大学机械结构强度与振动国家重点实验室西安，710049)(2.新疆大学机械工程学院乌鲁木齐，830047)

分数阶全息的转子起停车故障特征提取方法

杜小伟1，温广瑞1,2，江铖1，廖与禾1

(1.西安交通大学机械结构强度与振动国家重点实验室西安，710049)(2.新疆大学机械工程学院乌鲁木齐，830047)

针对传统起停车过程分析采用短时傅里叶变换提取瞬时幅值和相位会损失瞬变信息的不足，提出了基于分数阶全息原理的转子起停车故障特征提取方法。该方法利用分数阶傅里叶变换从转子起停车振动数据中提取随转速变化的各倍频分量，并通过Hilbert变换求取幅值和相位，克服了傅里叶变换的平均效应，保留了转子振动的瞬变信息。通过结合全息谱理论绘制分数阶全息瀑布图，提取出转子起停车状态下的故障特征。实验结果表明，该方法能够有效提取出起停车过程中振动信号的典型故障特征，对于常见的典型故障有很好的区分能力。

转子；起停车；分数阶傅里叶变换；分数阶全息瀑布图；故障特征提取

引言

对旋转机械故障特征的正确提取进而实现快速诊断，是工业生产平稳运行的重要保障[1]。目前，转子故障的识别诊断主要是基于稳态振动特征[2],还没有充分利用升降速过程中的振动信息。起停车过程中信号是非平稳的，直接使用傅里叶变换会出现频率模糊的现象。因此，针对起停车信号的分析必须采用能够处理非平稳信号的方法。

分数阶傅里叶变换(fractional Fourier transform, 简称FrFT)方法能够将与转速相关的各倍频分量提取出来。将分数阶傅里叶变换技术应用在起停车过程中能够提取出调幅调频的转频、倍频和分倍频分量。目前，较为常用的非平稳信号处理方法有短时傅里叶变换、魏格纳分布(Wigner-Vile distribution, 简称WVD)、小波分析和经验模态分解(empirical mode decomposition, 简称EMD)等。短时傅里叶将非平稳过程看成是短时窗内的平稳信号[3]，利用短时傅里叶变换和内插技术求出各时窗内信号的幅值频率和相位，必然存在幅值和相位误差。WVD具有处理非平稳信号的能力[4]，但由于双线性产生的干扰项非零，产生的一些现象不易解释。运用小波时需要从复杂的小波基中选择合适的小波基。EMD在启停车等非平稳信号特征参数提取方面得到成功运用[5]，然而EMD方法在提取分量时容易产生没有实际物理意义的分量。国内外研究人员提出了各种阶比跟踪算法并将其应用于非平稳信号处理，然而阶比分析方法在提取倍频分量时过程较为复杂，对于转速计算的精度要求高，且确定其滤波级数和带宽等参数的难度大。

传统的傅里叶变换是以三角函数为正交基在频域内展开，分数阶傅里叶变换[6-7]是以chirp基展开[8]。文献[9]将分数阶傅里叶变换的物理意义解释为信号的表示轴在时频平面内绕原点的旋转[9]。分数阶傅里叶变换首先应用在光学领域中[10]，并进一步应用在雷达和通信等信息系统中的线性调频信号[11-13]。通过在时频面内的旋转可以把在时域或频域内耦合的信号分离开来，因此分数阶傅里叶变换对于线性调频信号有很强的能量聚集特性，可以有效处理包括起停车信号和转速波动信号在内的线性调频信号。

全息谱是一种将多个传感器的振动信息在频域融合的方法，能够综合反映机组振动的幅值、频率和相位信息，在实际生产中能够比一般方法更为准确地识别转子故障[14-15]。笔者将分数阶傅里叶变换与全息谱原理相结合，将非稳态信号进行分数阶傅里叶变换提取主要倍频分量，根据Hilbert变换求取分量各转速下的振动幅值和相位，再结合全息谱分析的方法对转子启停机信号进行特征参数提取。

1 分数阶全息原理

1.1 分数阶傅里叶变换理论

在信号处理领域，传统傅里叶变换是一个最为成熟、应用最为广泛的数学工具。傅里叶变换是一种线性算子，若将其看作从时间轴逆时针旋转π/2到频率轴，则分数阶傅里叶变换算子就是可以旋转任意角度α的算子，并因此得到新的信号表示。

1.1.1 基本原理

设信号函数f(t)的分数阶傅里叶变换为Fpf(t)，分数阶Fourier变换的基本定义为

(1)

其中：p为阶数，为任意实数；Kp(t,u)为变换核。

Kp(t,u)=

(2)

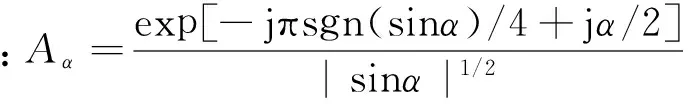
1.1.2 时频平面旋转和倍频分量提取

任意p阶的分数阶傅里叶变换可认为是将函数f(u)所在(t,ω)平面旋转角度α=pπ/2后映射到(v,u)平面的表达，如图1所示。当分数阶p=1时，有α=π/2，Aα=1，这时定义式就是普通的傅里叶变换。传统的傅里叶变换将函数f(u)旋转π/2，由t轴变到了ω轴。当分数阶p=0时，Fpf(t)=f(t)；当分数阶p=±2时，Fpf(t)=f(-t)。因此，分数阶傅里叶变换可认为是一种广义的傅里叶变换，且变换以参数p值为周期。

图1 (t,ω)时频平面和(v,u)分数阶域Fig.1 (t,ω)time frequency plane and (v,u)fractional Fourier domain

根据式(1)和时频平面旋转特性可知，分数阶傅里叶变换是将信号在一组正交的线性调频信号上展开，线性调频信号的某一阶次分数阶傅里叶变换是一个δ函数，因此在该阶次的分数阶傅里叶变换域中线性调频信号具有很好的能量聚焦特性。如果能找到相应的分数阶次，通过在该分数阶域的滤波，能够很好地提取和分离线性调频信号。

回转机械启停车过程中转速逐渐增加或减小，如果考虑转频振动和各倍频振动，启停车过程振动信号可近似认为是多个线性调频信号之和。如果能找到合适的分数阶次，通过在该分数阶域的滤波，可很好提取和分离线性调频信号。

1.2 全息谱基本理论

全息谱方法是一种在数据层进行信息融合的方法，将一个截面两个相互垂直测点的振动信息在频域进行融合。二维全息谱原理及构成如下。

转子测量面互相垂直的两个方向，振动信号的第i个主要频率分量的参数方程为

(3)

其中：αi，βi为x，y两方向第i个主要频率的相位；Ai，Bi为x，y两方向第i个主要频率的幅值；fi为主要频率分量的旋转频率。

将转子某个测量面上水平和垂直两方向的振动信号分别进行FFT，得到主要频率分量的频率幅值和相位。经过频谱校正后得到精确值，利用各个主要频率的幅值和初相位，绘制出对应频率分量的全息椭圆并排列在一张谱图上，即形成二维全息谱。

2 关键参数分数阶p的选取方法

如果能找到合适的分数阶次在该分数阶域的滤波，则可以提取线性调频信号。由时间-频率平面的旋转定义可知，旋转角度α=pπ/2，而α与升速比fmi存在以下关系

(4)

进而求得

(5)

由于在时频平面上的量纲不同，所以必须要先对时频平面内的频率和时间进行归一化处理，将坐标系转化为无量纲的域。实际归一化后的升速比fmi为

(6)

进而有

(7)

其中:T为信号时间；fs为信号的采样频率。

直接使用由升速比求得的分数阶次p进行实际信号的分数阶傅里叶变换时，由于实际求升速比的过程中存在误差，所以需要对分数阶次p进行优化。以实验台实际启停车信号为例，图2为未对分数阶次p进行优化时的分数阶傅里叶变换v域图。可以看到，此时的分数阶傅里叶对于线性调频信号的能量聚集性并不是很强。

图2 参数未优化的分数阶傅里叶变换v域Fig.2 Fractional Fourier domain with unoptimized parameter

对p值进行单目标优化，使得分数阶域幅值最大。由多次实验确定优化区间为(p-0.01, p+0.01),步长为0.000 5，最后得到优化后的分数阶p，做出此时的分数阶傅里叶变换v域图。从图3可以看出，此时的分数阶傅里叶对于线性调频信号的能量聚集性很强，能有效处理线性调频信号。

图3 参数优化后的分数阶傅里叶变换v域图Fig.3 Fractional Fourier domain with optimized parameter

3 转子典型故障特征提取

由于转子的故障特征频率主要表现在转频、倍频和分倍频，所以对于起停车过程振动信号，提取出相应的倍频分量也必然能够表现出故障特征。基于分数阶傅里叶变换的4种典型转子起停车故障特征提取流程如图4所示。

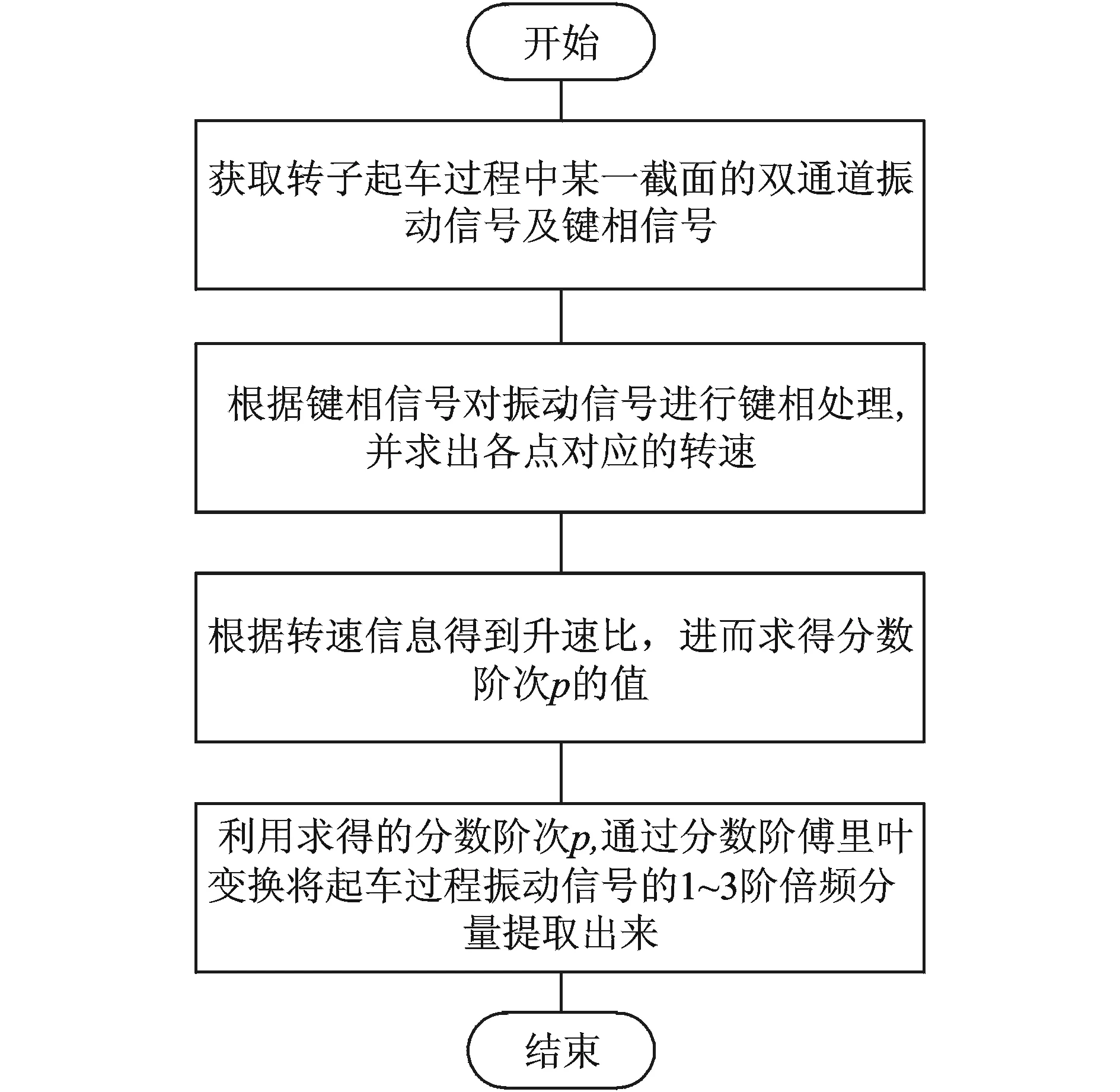
图4 基于FrFT的转子起停车故障特征提取流程图Fig.4 Flow chart of fault feature extraction for rotor star-up or slowdown process based on FrFT

在Bently RK4转子实验台上对笔者提出的方法进行验证，模拟不对中和转子裂纹故障并采集起停车信号，进行分数阶傅里叶变换提取出0.5～3倍频分量，提取出各倍频分量绘制全息瀑布图。为了充分考虑转子支撑各向异性的影响，分别在A,B两测量面上安装相互垂直的电涡流传感器，实验台结构和传感器的安装方式如图5所示。设置采样频率为2 048 Hz，采样时长为15 s，选择合适的升速比，用DT9837B数采卡对转子起停车过程进行连续数据采集，测量得到转子系统在300 r/min～4 kr/min范围内的起停车数据。

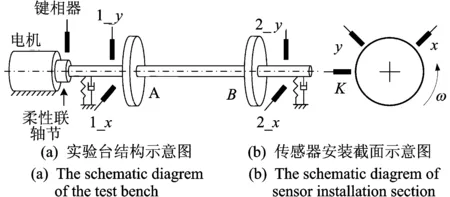
图5 传感器安装示意图Fig.5 The schematic diagram of sensor installment

3.1 不平衡故障

进行不平衡故障模拟时，在配重盘加上不平衡质量，采集转速从300r/min～5 kr/min的起停车数据，绘制分数阶全息瀑布图如图6所示。可以看出转子不平衡的主要特征：a.仅有大的1倍频分量；b.1倍频临界转速下的振动大；c.椭圆偏心率小；d.过临界相位翻转180°；e.接近临界转速两侧椭圆的倾斜方向相反。

图6 不平衡故障分数阶全息瀑布图Fig.6 Fractional holo-waterfall diagram for unbalance fault

3.2 不对中故障

模拟不对中故障时，将电机用垫片垫高，采集转速从300r/min～5 kr/min的起停车数据，绘制分数阶全息瀑布图如图7所示。可以看出转子不对中故障的主要特征：a.1倍频椭圆偏心率较大；b.2倍频分量较大且椭圆偏心率较大；c.2倍频存在亚临界共振且随转速变化较大；d.0.5倍频存在2阶临界共振。

图7 不对中故障分数阶全息瀑布图Fig.7 Fractional holo-waterfall diagram for misalignment fault

3.3 裂纹故障

模拟裂纹故障时，加工裂纹转子，裂纹在轴的中部，大小约为1/4的转子直径，采集转速从300r/min～4 kr/min的起停车数据，绘制分数阶全息瀑布图如图8所示。可以看出转子裂纹故障的主要特征：a.1倍频分量较大且椭圆偏心率小，过临界相位翻转180°；b.1倍频与不平衡相近；c.2倍频分量较大且椭圆偏心率小；d.出现2，3倍频亚临界共振，振幅变化不大。

图8 裂纹故障分数阶全息瀑布图Fig.8 Fractional Holo-waterfall diagram for crack fault

3.4 碰磨故障

模拟碰磨故障时，在本特利转子动平衡实验台的转轴中部固定一个橡胶摩擦棒，进行碰磨故障模拟，采集转速从300r/min～4 kr/min的起停车数据，绘制分数阶全息瀑布图如图9所示。可以看出转子碰磨故障的主要特征：a.1倍频椭圆偏心率很大；b.1倍频椭圆倾斜方向几乎一致；c.1倍频出现反进动；d.2倍频存在亚临界共振。

图9 碰磨故障分数阶全息瀑布图Fig.9 Fractional holo-waterfall diagram for friiction fault

通过4种模拟故障的分数阶全息瀑布图，总结出了转子典型故障的特征：碰磨故障的1倍频椭圆偏心率最大，加上其反进动的特点，是最容易进行区分的故障特征；不对中故障1倍频椭圆偏心率较大，和碰磨接近,可以通过其2倍频分量较大且椭圆偏心率较大这一明显特征进行区分；不平衡和裂纹故障的1倍频分量都较大且偏心率小，这一特征两者较为接近；裂纹故障的2，3倍频亚临界共振比较大，可以和不平衡故障进行区分。综上所述，通过分数阶傅里叶变换与全息谱结合的方法可以很好地突出故障特征，对于涉及的4种典型故障有较好的区分能力。

4 结束语

利用分数阶全息原理对转子起停车过程的故障特征提取方法进行研究，提出了基于分数阶全息原理的全息瀑布图方法进行转子故障特征提取，并进行了一系列的实验验证。该方法对转子启停车过程非平稳振动信号进行滤波并得到转子振动的各倍频分量。各故障的识别特征有较明显区别，其中不平衡、裂纹故障与其他各类故障的区分很明显，能够有效地对振动信号进行故障特征提取。相比于传统的短时傅里叶变换等非平稳信号处理方法，分数阶全息原理能够提取出起停车过程中振动信号的各倍频分量，很好地保留了瞬变信息，对于常见的典型故障有很好的区分能力。

[1] 韩捷,张瑞林. 旋转机械故障机理及诊断技术[M]. 北京:机械工业出版社,1996:91-92.

[2] 孙惠国,张瑞林. 设备状态监测与故障诊断[M]. 郑州:河南科学技术出版社,1992:23-29.

[3] 边海龙,陈光禹. 基于短时傅里叶变换检测非平稳信号的频域内插优化抗混叠算法[J].仪器仪表学报,2008,29(2):284-288.

Bian Hailong, Chen Guangyu. Anti-aliasing algorithm of nonstationary harmonic signal measurement based on interpolation in frequency domain using short time Fourier transform [J]. Chinese Journal of Scientific Instrument, 2008,29(2):284-288.(in Chinese)

[4] 陈涛. 小波分析理论及其在机械监测与诊断中的应用研究 [D]. 西安:西安交通大学,1997.

[5] 祁克玉. 经验模式分解方法及其在旋转设备故障诊断中的应用 [D]. 西安:西安交通大学,2004.

[6] 陶然,齐林,王越. 分数阶Fourier变换的原理与应用[M]. 北京：清华大学出版社,2004:23-26.

[7] 陶然,邓兵,王越. 分数阶Fourier变换在信号处理领域的研究进展[J]. 中国科学E辑：信息科学,2006,36(2):131-136.

Tao Ran, Deng Bin, Wang Yue. The progress of the fractional Fourier transform in signal processing[J]. Science in China Ser. E： Information Sciences, 2006,36(2):131-136.(in Chinese)

[8] Namias V.The fractinal order Fourier transform and its application to quantum mechanics[J].Journal of the Institute of Mathematics Antits Applications,1980,25: 241-265.

[9] Almeida L B. The fractional Fourier transform and time-frequency represe ntations[J]. IEEE Transcation Signal Processing, 1994,42(11):3084-3091.

[10]Ozaktas H M, Arikan O, Kutay A, et al.Digital computation of the fractional Fourier transform[J]. IEEE Transcation Signal Processing,1996,44(9):2141-2150.

[11]梅检民,肖云魁,陈祥龙,等. 基于FRFT的单分量阶比双谱提取微弱故障特征[J]. 振动、测试与诊断,2012,32(4):655-660.

Mei Jianmin, Xiao Yunkui, Chen Xianglong, et al. Weak fault characteristic extraction by single component order bispectrum based on fractional Fourier transform[J]. Journal of Vibration， Measurement & Diagnosis,2012,32(4):655-660.(in Chinese)

[12]徐会法,刘锋,张鑫. 分数阶Fourier域强弱LFM信号检测与参数估计[J]. 信号处理,2011, 27(7):1063-1068.

Xu Huifa, Liu Feng, Zhang Xin. Detection and parameter estimation of strong and weak LFM signals in the fractional Fourier domain[J]. Signal Processing, 2011, 27(7):1063-1068.(in Chinese)

[13]周绍磊,廖剑,史贤俊. 基于FrFT-FD和KPCA模拟电路故障特征提取方法[J]. 振动、测试与诊断,2014,34(2):337-344.

Zhou Shaolei, Liao Jian, Shi Xianjun. New method to extract analog circuit fault Features based on FrFT-FD and KPCA[J]. Journal of Vibration, Measurement & Diagnosis,2014,34(2):337-344.(in Chinese)

[14]屈梁生. 机械故障的全息诊断原理[M]. 北京：科学出版社,2007:6-12.

[15]屈梁生，张西宁，沈玉娣. 机械故障诊断理论与方法[M]. 西安：西安交通大学出版社,2009:145-153.