浓度对光脉动法气固两相流颗粒粒径测量的影响

杨斌，何渊，周骛，姜勇俊，蔡小舒

(上海理工大学 颗粒与两相流测量研究所，上海市动力工程多相流动与传热重点实验室，上海，200093)

浓度对光脉动法气固两相流颗粒粒径测量的影响

杨斌，何渊，周骛，姜勇俊，蔡小舒

(上海理工大学 颗粒与两相流测量研究所，上海市动力工程多相流动与传热重点实验室，上海，200093)

针对工业应用中气固两相流浓度对光脉动(LTF)颗粒粒径测量方法的影响问题，通过对比浓度基本不变及浓度时刻变化的光脉动频谱特征，分析确定因浓度变化造成影响的阈值频率，由此提出高通滤波光脉动法颗粒粒径优化算法，并将该算法用于浓度时刻变化的光脉动法数据处理中。研究结果表明：优化算法结果与激光粒度仪离线测量结果相对偏差改进到12%内，且标准差降低为11.3 μm，由此验证了该算法可有效减小浓度对光脉动法测量结果的影响，提高测量结果的准确性和稳定性。

气固两相流；在线测量方法；光脉动法；颗粒粒径；浓度影响

气固两相流气力输运广泛存在于能源、环境和化工领域中，其过程的优化控制与运行需实现气固两相流参数的实时在线测量[1−2]。颗粒的粒径为其中最重要的参数之一，直接影响气固两相流流动情况、气力输运能力等[3−4]。目前，气固两相流颗粒的粒径在线测量方法主要有超声法、图像法和光散射法等[5−7]。其中，光脉动法(light transmission fluctuation, LTF)是利用透射光强随机变化规律结合光散射理论的气固两相流颗粒粒径测量方法[8−10]，因具有结构简单、对测量环境要求低、长时间运行可靠等优点，更适合工业现场的在线监测。目前，光脉动法已在电站锅炉煤粉气力输运、水泥生料制备输运、石油化工催化剂添加等领域进行了应用探索[11−13]。在实际应用过程中，由于工业过程中气固两相流中颗粒浓度通常时刻发生变化，随浓度变化造成的光强脉动会与因颗粒大小造成的光强脉动叠加，造成光脉动法颗粒粒径测量结果偏大，给测量的准确度和稳定性都带来不利影响[14]。针对这一问题，本文作者通过对比浓度基本不变及浓度时刻变化的光脉动信号来研究浓度变化对光脉动法颗粒粒径测量的影响，并提出消除浓度变化影响方法，以提高光脉动法测量结果的准确性和稳定性。

1　光脉动法测量原理

光脉动法气固两相流颗粒粒径测量基本原理是：当光束照射气固两相流时，照亮测量区域内的颗粒数随时间变化，造成透射光强出现脉动信号。将不同时刻光束照亮测量区域内的颗粒数作为随机事件，建立颗粒粒径及颗粒数与透射光强的关系，便可实现对气固两相流颗粒粒径的在线测量。

光脉动法测量原理示意图如图1所示。由图1可见：当一束平行单色光照射气固两相流被测颗粒时，由于颗粒的散射和吸收，透射光强将会衰减，衰减量符合Beer−Lambert定律，即

其中：Γ为对数透射率，为透射光强It与入射光强I0的对数比；L为测量光束在测量区内的光程，m；N为单位体积颗粒数浓度，m3，当光束面积为A时，该时刻激光照射颗粒数n=NAL；D为颗粒的平均粒径，m；kext为消光系数，它是入射光波长λ、颗粒平均粒径D和颗粒相对折射率m的函数，可由米氏散射理论求得[15−16]。

定义Sext为颗粒的消光面积为

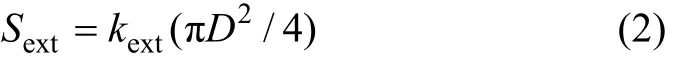
代入式(1)得

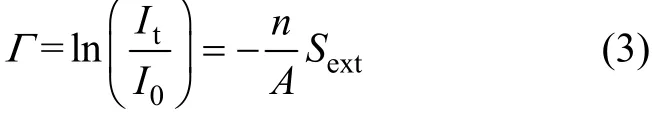
若减小光束的截面积A，某一时刻被照射颗粒数n也会相应减小，当n减至一定程度时，呈现随机性，相应的透射光强It出现脉动信号。可以认为n符合泊松分布，可得E(n)=D(n)。因此，可以建立对数透射率Γ与颗粒数n之间的统计学关系：

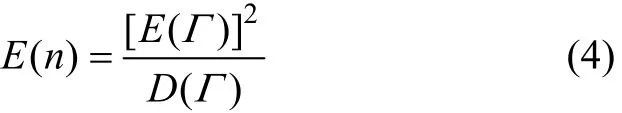
将式(3)代入式(4)可求得颗粒消光面积Sext，由此便可计算颗粒的平均粒径D为

因此，通过测量入射光强与透射光强信号，依据建立的颗粒粒径与光脉动信号的关系，便可实现对气固两相流颗粒粒径的在线测量。

2　测量系统与实验装置

图2　光脉动法颗粒粒径在线测量系统示意图Fig. 2 Schematic diagram of in-line particle size measurement system based on LTF

光脉动法气固两相流颗粒粒径在线测量系统如图2所示。由图2可见：测量探针采用凹槽结构设计，激光器由探针座发出，经小孔照射测量区域后，由探测器接收，利用计算机记录光脉动信号并处理得到气固两相流颗粒粒径。为模拟气固两相流浓度变化，设计气固两相流装置如图3所示，将煤粉装入料仓，通过调节阀门开口截面来改变煤粉下料质量，以模拟不同浓度的煤粉气固两相流。

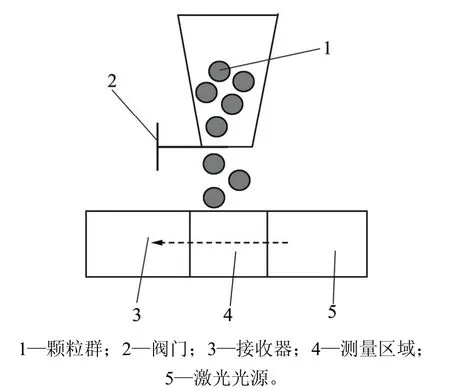
图3　实验装置示意图Fig. 3 Schematic diagram of experimental device

3　浓度变化影响研究

3.1光脉动信号现象分析

实验获得浓度基本不变及浓度时刻变化的光脉动信号如图4所示。由图4可以看出：对于浓度基本不变的信号，其频率较高，且在均值附近波动，其幅值较小；对于浓度时刻变化的信号，其存在高频信号的同时，还出现低频大幅波动。因此，2种条件下光脉动信号频谱存在明显差异。

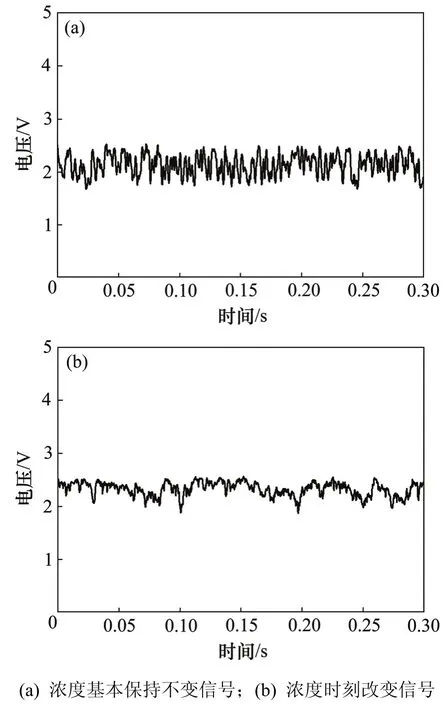
图4　不同浓度条件下透射光强信号Fig. 4 Comparison of signals on different concentration conditions

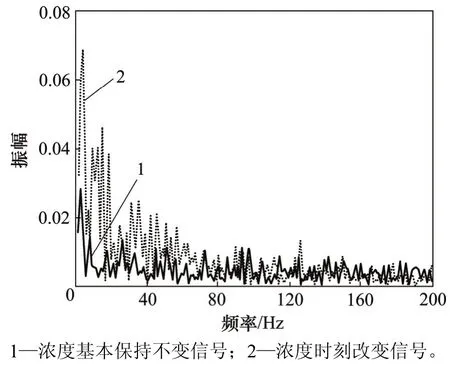
图5　信号振幅谱图Fig. 5 Schematic of signal amplitude spectrum

3.2频谱分析

对这2组典型信号进行快速傅里叶变换(fast Fourier transformation, FFT)振幅谱分析，结果如图5所示。从图5可以看出：当频率大于75 Hz时，2种浓度下光脉动信号振幅幅值基本相当；当频率小于75 Hz时，2种浓度下光脉动信号振幅幅值存在明显差异。由此可知，浓度的改变仅影响频率小于75 Hz的光脉动信号，对于大于75 Hz的光脉动信号可以认为是颗粒流经测量区域造成。进一步分析频率小于75 Hz光脉动信号频谱，对于浓度时刻变化条件下的光脉动信号，频谱幅值随着频率的减小而大幅增大，可以认为这是由于浓度变化造成信号低频大幅值变化。而对于浓度基本保持不变条件下的光脉动信号，大部分频谱幅值与高于75 Hz的频谱幅值相当，可以认为这是大颗粒或多个颗粒叠加所造成，而对于低于10 Hz频率频谱幅值仍较大的情况，是因为此时浓度仍存在小变化。因此，75 Hz可以作为因浓度变化造成光脉动信号频率变化的低频阈值频率。但是这一阈值频率并不具有普适性，它由颗粒的粒径和速度决定，其数学关系模型有待进一步研究。在目前的工业应用中，阈值的确定方法是将一段时间的原始信号进行分析，结合取样分析结果进行对比，最终确定这一阈值频率。

3.3算法优化

以75 Hz作为因浓度变化造成光脉动信号频率变化的低频阈值频率对浓度变化条件下的光脉动信号进行分解，如图6所示。由图6可以看出：高频部分信号可认为因颗粒流经测量区域造成，可以用作颗粒粒径计算以提高测量结果的准确性和稳定性；对于低频部分，主要是因为浓度变化造成衰减强度的低频变化，对于粒径计算应予以消除，但对于双光束光脉动法相关原理测量颗粒速度来说，用其作为分析信号可以有效提高互相关计算的效率。通过上述分析，可以提出消除浓度影响的颗粒粒径测量优化算法，即采用高通滤波方式预先对光脉动原始信号进行处理后再计算颗粒粒径。

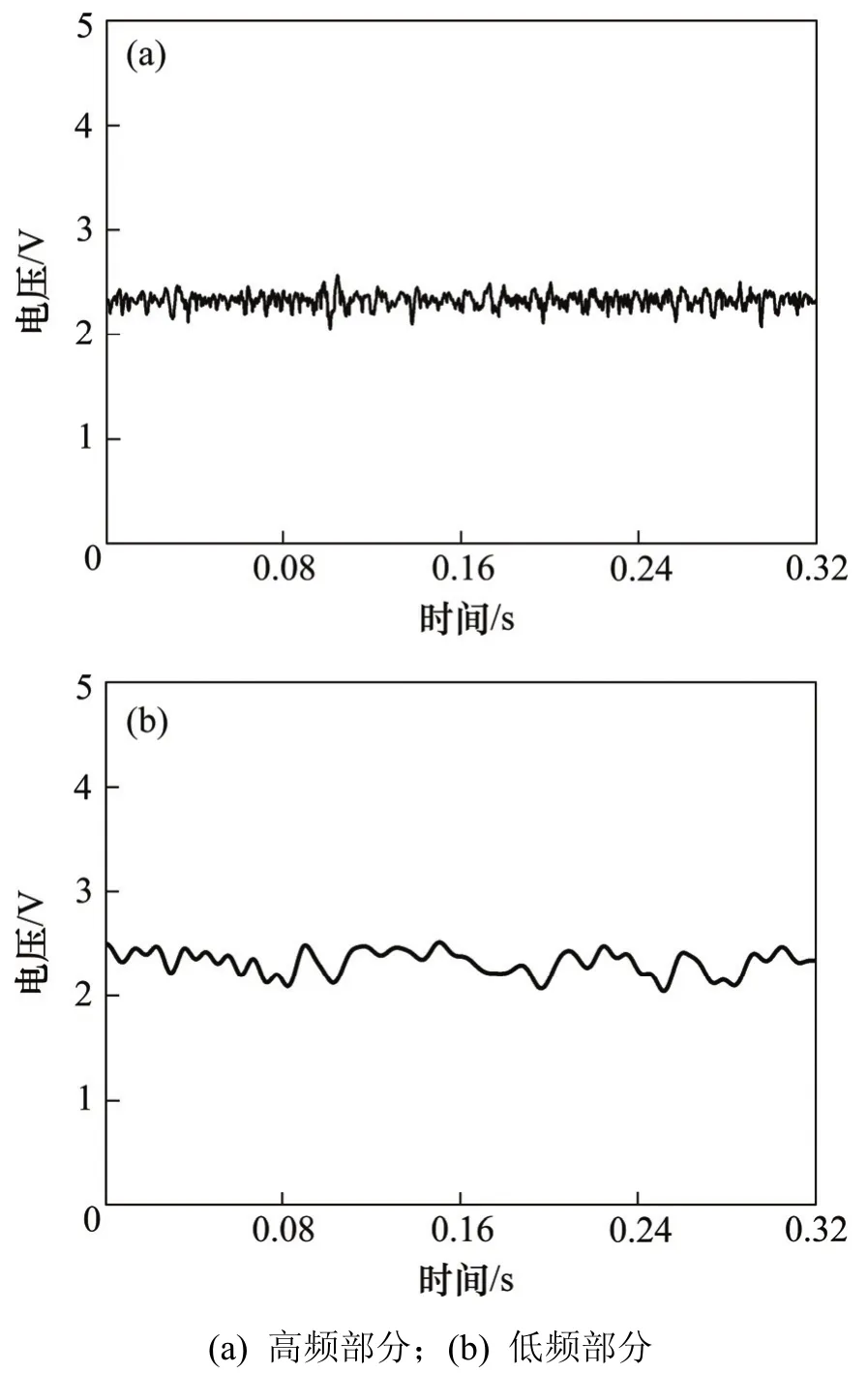
图6　信号高频与低频部分信号Fig. 6 Signals at high and low frequencies

3.4对比验证

将优化算法应用于42组浓度变化条件下光脉动信号的处理，对比通过原始算法与优化算法处理结果如图7所示。由图7可知：通过原始算法处理的42组测量结果平均值为87.78 μm，标准差为18.80 μm；通过优化算法处理的42组测量结果平均值为52.70 μm，标准差为11.30 μm。选取样品煤粉，利用激光粒度仪(Malvern APA2000)对煤粉颗粒粒度进行测量，典型测量结果如图8所示，因基于光脉动法测量所得结果为颗粒的平均粒径，取激光粒度仪5次平均粒径测量结果的平均值(47.49 μm)作为对比参考值进行分析。

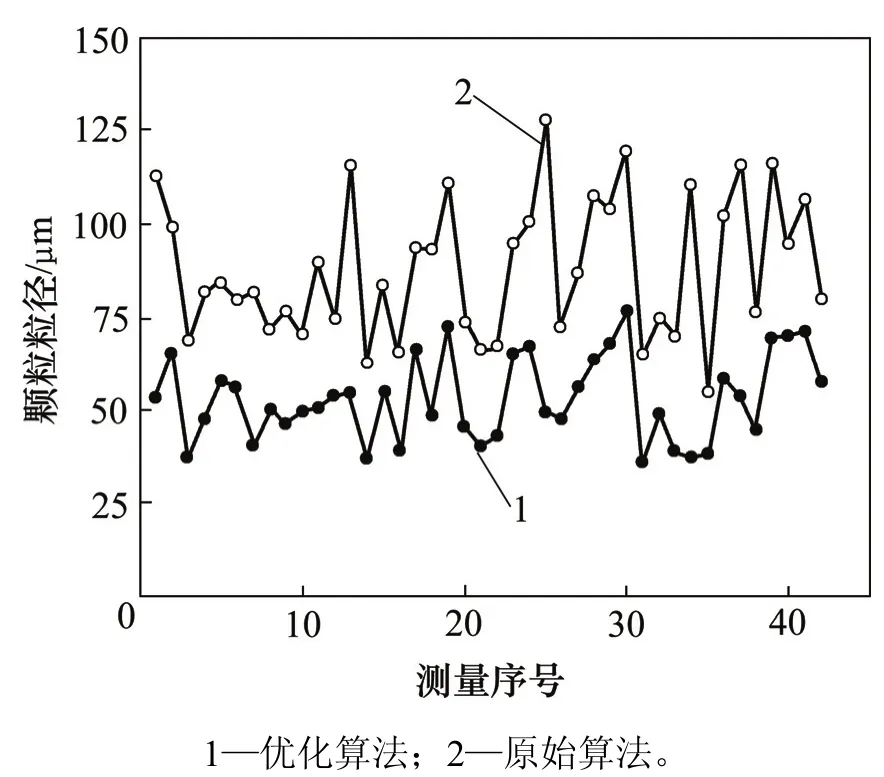
图7　2种算法所得颗粒粒径对比图Fig. 7 Comparison of particle sizes by using two algorithms

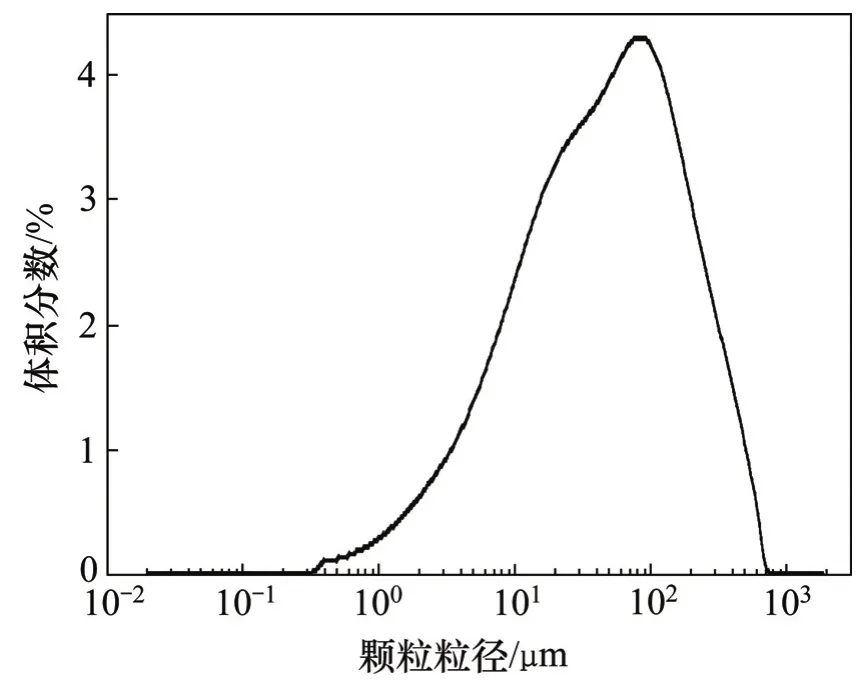
图8　激光粒度仪测量结果图Fig. 8 Measurement result of pulverized coal by particle size analyzer

将原算法与优化算法处理结果与参考值对比，如表1所示。由表1可以看出：对于浓度改变条件下的光脉动实验结果，优化算法可使处理结果与平均值的相对偏差降低到10.9%，有效提高了测量准确性；另外，优化算法使42组测量结果标准差降为11.30 μm，有效提高了测量的稳定性。

表1　2种算法所得颗粒粒径对比Table 1 Comparison of particle sizes by using two algorithms

4　结论

1) 通过对比浓度基本不变与时刻改变情况下光脉动法透射信号特征发现：因浓度变化造成的光脉动信号具有低频高幅值特征，因粒径变化造成的信号具有高频低幅值特征。

2) 通过对比两者振幅谱特征，确定了浓度变化影响光脉动信号特征的阈值频率，由此提出了光脉动法高通滤波优化算法。

3) 通过激光粒度仪测量对比，验证了优化算法可有效减小浓度对光脉动法测量结果的影响，提高了测量结果的准确性和稳定性。

[1] 车得福, 李会雄. 多相流及其应用[M]. 西安: 西安交通大学出版社, 2007: 3−50. CHE Defu, LI Huixiong. Multiphase flow and its applications[M]. Xi’an: Xi’an Jiaotong University Press, 2007: 3−50.

[2] 滕汜颖, 李永光, 周伟国, 等. 气固两相流动测量技术的现状与展望[J]. 上海电力学院学报, 2002, 18(4): 39−43. TENG Siying, LI Yongguang, ZHOU Weiguo, et al. Present & prospective techniques for gas-solid two-phase flow measurement[J]. Journal of Shanghai University of Electric Power, 2002, 18(4): 39−43.

[3] 王乃宁. 颗粒粒径的光学测量技术及应用[M]. 北京: 原子能出版社, 2000: 370−374. WANG Naining. Optical measurement techniques and applications for particle size[M]. Beijing: Atomic Press, 2000: 370−374.

[4] 林宗虎, 王栋, 王树众, 等. 多相流的近期工程应用趋向[J].西安交通大学学报, 2001, 35(9): 886−890. LIN Zonghu, WANG Dong, WANG Shuzhong, et al. Recent trend towards engineering application of multiphase flow[J]. Journal of Xi’an Jiaotong University, 2001, 35(9):886−890.

[5] 蔡小舒, 苏明旭, 沈建琪. 颗粒粒度测量技术及应用[M]. 北京: 化学工业出版社, 2010: 336−355. CAI Xiaoshu, SU Mingxu, SHEN Jianqi. Measurement techniques and applications for particle size[M]. Beijing: Chemical Industry Press, 2010: 336−355.

[6] 田昌, 苏明旭, 蔡小舒. 基于超声法测量气固两相流浓度实验研究[J]. 工程热物理学报, 2013, 34(8): 1487−1490. TIAN Chang, SU Mingxu, CAI Xiaoshu. Particle concentration characterization in gas-solid two-phase flow by ultrasonic methods[J]. Journal of Engineering Thermophysics, 2013, 34(8): 1487−1490.

[7] 张晶晶, 范学良, 蔡小舒. 单帧单曝光图像法测量气固两相流速度场[J]. 工程热物理学报, 2012, 33(1): 79−82. ZHANG Jingjing, FAN Xueliang, CAI Xiaoshu. Measurement for velocity field of gas-solid two phase flow using single frame and single exposure imaging[J]. Journal of Engineering Thermophysics, 2012, 33(1): 79−82.

[8] SHIFRIN K S, SAKHAROV A N. Determination of the average size and concentration of suspended particles from intensity fluctuations of transmitted light[J]. Optics and Spectroscopy, 1975, 39(2): 208−210.

[9] GREGORY J. Turbidity fluctuations in flowing suspensions[J]. Journal of Colloid and Interface Science, 1985, 105(2): 357−371.

[10] QIN Shouxuan, CAI Xiaoshu. Indirect measurement of the intensity of incident light by the light transmission fluctuation method[J]. Optics Letters, 2011, 36(20): 4068−4070.

[11] CAI Xiaoshu, LI Junfeng, OUYANG Xin, et al. In-line measurement of pneumatically conveyed particles by a light transmission fluctuation method[J]. Flow Measurement and Instrumentation. 2005, 16(5): 315−320.

[12] 蔡小舒, 李俊峰, 欧阳新, 等. 光脉动法煤粉实时在线监测技术进展[J]. 华北电力大学学报, 2003, 30(6): 38−42. CAI Xiaoshu, LI Junfeng, OUYANG Xin, et al. Progress on on-line monitoring of pulverized coal in power station based on LTF[J]. Journal of North China Electric Power University, 2003, 30(6): 38−42.

[13] 蔡小舒, 李俊峰, 欧阳新, 等. 在美国Bull Run电厂900 MW锅炉上风粉在线测量试验[J]. 热力发电, 2005, 34(5): 24−26, 64. CAI Xiaoshu, LI Junfeng, OUYANG Xin, et al. On-line measurement test of air/fuel for 900 MW boiler in bull run power plant of USA[J]. Thermal Power Generation, 2005, 34(5): 24−26, 64.

[14] 黄春燕, 蔡小舒, 赵志军, 等. 电站煤粉光脉动信号的小波分析及粒度计算[J]. 仪器仪表学报, 2004, 25(增2): 507−508, 524. HUANG Chunyan, CAI Xiaoshu, ZHAO Zhijun, et al. Wavelet analysis and granularity calculation of coal powder fluctuating light signals at power plant[J]. Chinese Journal of Scientific Instrument, 2004, 25(Suppl 2): 507−508, 524.

[15] 王亚伟. 光散射理论及其应用技术[M]. 北京: 科学出版社, 2007: 21−47. WANG Yawei. Light scattering theory and its application technology[M]. Beijing: Science Press, 2007: 21−47.

[16] 项建胜, 何俊华. Mie光散射理论的数值计算方法[J]. 应用光学, 2007, 28(3): 363−366. XIANG Jiansheng, HE Junhua. Numerical calculation of Mie theory[J]. Journal of Applied Optics, 2007, 28(3): 363−366.

(编辑 刘锦伟)

Concentration influence on light transmission fluctuation method for particle size measurement of gas-solid two-phase flow

YANG Bin, HE Yuan, ZHOU Wu, JIANG Yongjun, CAI Xiaoshu
(Institute of Particle and Two-phase Flow Measurement, Shanghai Key Laboratory of Multiphase Flow and Heat Transfer in Power Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China)

For the influence on the light transmission fluctuation (LTF) method of particle concentration for the particle size measurement in industrial applications, the frequency spectrum characteristics were analyzed by comparing the steady particle concentration condition with the unsteady condition, and the threshold frequency caused by unsteady concentration was obtained. Thus, the high-pass filtering optimum algorithm of LTF was presented for particle size calculation. The results show that the relative deviation between optimum algorithm and original algorithm is improved within 12%, and the standard deviation is reduced to 11.3 μm. The influence on LTF of particle concentration can be decreased by the optimum algorithm effectively, and the accuracy and reliability of measurements are improved respectively.

gas-solid two-phase flow; in-line measurement; light transmission fluctuation method; particle size; concentration influence

TH89

A

1672−7207(2016)03−1044−05

10.11817/j.issn.1672-7207.2016.03.043

2015−03−15；

2015−05−07

国家自然科学基金资助项目(50836003)；上海市科委科研计划项目(13DZ2260900)；上海高校青年教师培养资助计划项目(ZZslg15002) (Project(50836003) supported by the National Natural Science Foundation of China; Project(13DZ2260900) supported by the Shanghai Science and Technology Commission; Project(ZZslg15002) supported by the Shanghai Young University Teachers Training Program)

周骛，博士，讲师，从事多相流与燃烧在线测量方法研究；E-mail: zhouwu@usst.edu.cn