2种应力波信号增强方式在预应力锚杆(索)锚固质量检测中的适用性研究
2016-12-07邓东平李亮赵炼恒
邓东平,李亮,赵炼恒
(中南大学 土木工程学院,湖南 长沙,410075)
2种应力波信号增强方式在预应力锚杆(索)锚固质量检测中的适用性研究
邓东平,李亮,赵炼恒
(中南大学 土木工程学院,湖南 长沙,410075)
由于随着锚杆(索)长度的增长,采用应力波法在端头接收到判别锚固体质量(锚杆(索)长度和锚固体断面变化处位置)的脉冲信号越弱,为了使此法同样适用于较长锚杆(索)的锚固质量检测,需增强端头接收到的应力波信号,为此,选择2种应力波信号增强方式(第1种为端头发射脉冲信号底端放大,第2种为端头和底端同时发射脉冲信号),然后,以锚杆(索)和注浆体组成的复合体计算应力波传播速度,并考虑应力波随传播时间呈对数螺旋衰减规律,采用特征线法计算得到简便判别锚固体质量的应力波信号时间和在端头接收到底端和锚固体断面变化处的应力波信号的速度,研究均匀断面全长注浆型、存在自由段非全长注浆型和存在缺陷段全长注浆型这3种特殊锚固体算例。研究结果表明:除锚固体断面变化处的位置离端头较近外,第2种信号增强方式均有适合简便判断锚固体质量的脉冲信号时间,而第1种信号增强方式仅在锚固体断面变化处的位置离端头较远时才存在;采用第2种信号增强方式时,在端头接收到反映锚杆(索)长度和锚固体断面变化处位置的脉冲信号均为端头或底端脉冲信号经各断面变化处传播到端头所用时间最短的信号,故所采集的脉冲信号均强于第1种信号增强方式所获得的信号;由于第2种信号增强方式存在1对相向传播的应力波信号,且各信号均能反映锚固体质量信息,故在实际操作中,需利用端头和底端发射不同频率的应力波信号加以区分。
预应力锚杆(索);应力波;特征线法;锚固体;脉冲时间;激发方式
在工程中,为增强边坡的稳定性,大量采用预应力锚杆(索)对其进行加固。然而,锚杆(索)均埋设于岩土体内,且锚孔内注浆属于隐蔽工程,因此,预应力锚杆(索)能否有效地对边坡形成加固效应,需对其进行质量检测[1]。在锚杆(索)锚固质量检测中,传统的方法具有破坏性,且操作麻烦,实验费用昂贵[2−4]。随着无损检测技术的发展,应力波反射法[5−10]在锚杆(索)质量检测中得到了广泛应用,其原理是在锚杆(索)端头激发应力波信号源,并通过在端头采集由不同锚固体部位反射回的应力波信号,然后对其进行时域、频谱及能量衰减分析,进而由分析结果对锚杆(索)的锚固质量进行快速评价[11−14],故应力波反射法具有经济、快速、简便和准确性较高等优点。目前,采用应力波反射法对锚杆(索)及注浆体组成的锚固体进行质量检测的2个主要参数是锚杆(索)长度和灌浆质量。随着边坡加固技术的成熟及处理边坡的大型化和复杂化,加固预应力锚杆(索)的长度也越来越长。由于应力波在传播过程中会产生信号衰减,并随锚杆(索)长度的增长,应力波在其传播的时间也增长,从而引起应力波信号衰减得更多,导致在锚固体端头接受不到有效的应力波信号,故阻碍了应力波反射法的适用性。为了使应力波反射法同样可对较长锚杆(索)进行有效质量检测,需对应力波信号采取增强措施。通过上述分析,本文采取2种应力波信号增强方式:1) 端头发射应力波信号底端放大;2) 端头和底端同时发射应力波信号。考虑3种特殊锚固体(即均匀断面全长注浆型、存在自由段非全长注浆型和存在缺陷段全长注浆型锚固体),分析满足简便判断锚固体质量(即锚杆(索)长度和锚固体断面变化处位置)的应力波信号时间,并基于特征线法计算此2种应力波信号增强方式在锚固体端头接受到由底端和锚固体断面变化处反射(或透射)回的应力波振动速度。同时,在计算过程中,采用复合锚固体模型计算应力波的传播波速,并对应力波能量随传播时间的震减规律采用数螺旋衰减规律,最后通过算例,研究该2种信号增强方式的适用性。
1 锚固体质量应力波检测法理论分析
1.1应力波传播的特征线法
对于预应力锚杆(索)及其系统,可将预应力锚杆(索)及周围注浆体所组成的锚固体等效为一维弹性体杆件。
应力波沿特征线传播计算模型如图1所示。在一维平面波中,D′ Alembert通过理论分析得到应力波的波动解为以同一速度c传播的1个右行波和1个左行波这2行波叠加而成[15],即应力波的波动解为
u(x, t)=F(x−ct)+G(x+ct)(其中,u为应力波在x位置t时刻的位移;c为应力波在弹性体中的传播波速,;E和ρ分别为弹性体的弹性模量和质量密度)。设ξ=x−ct和η=x+ct,当ξ和η均为常数(用符号const表示)时,在x−t平面上形成ξ和η的2族特征线,而F波即为沿特征线ξ=x−ct传播的右行波;G波即为沿特征线η=x+ct传播的左行波。
通过分析应力波沿特征线传播的规律,得到如下相容关系:
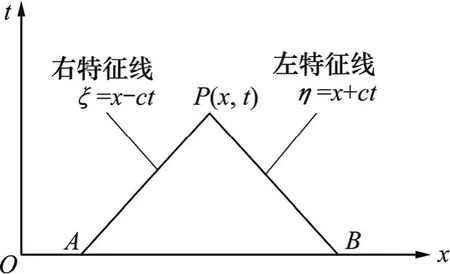
图1 应力波沿特征线传播计算模型Fig. 1 Calculation model of stress wave spreading along feature line
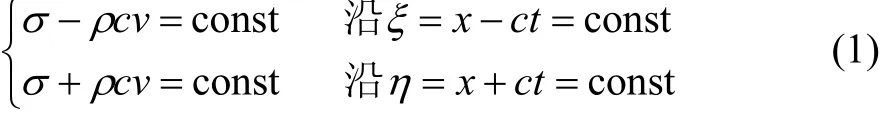
由式(1)可知:当应力波沿右(或左)特征线传播时,若在同一弹性体中其应力(或速度)不变,则其速度(或应力)也不变。同时,若已知右(或左)特征线上任一点的速度和应力,则可根据另一点的速度(或应力)求得该点的应力(或速度)。故利用此特征线相容关系可在已知初始和边界条件下,分析应力波x−t平面上其他各点的应力和速度。
1.2锚固体等效模型
锚固体等效计算模型如图2所示。当锚固体由预应力锚杆(索)和外围注浆体组成时,设预应力锚杆(索)的半径为r,弹性模量为Es,质量密度为ρs;外围注浆体的外半径为R,弹性模量为Ec,质量密度为ρc。
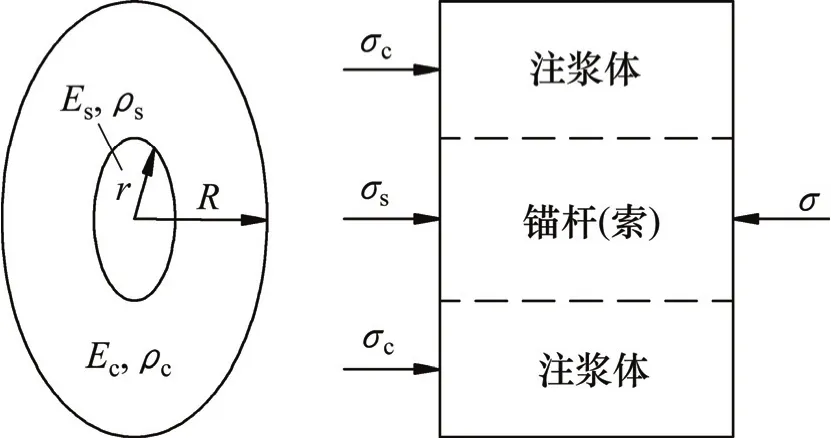
图2 锚固体等效计算模型Fig. 2 Equivalent computational model of anchorage body
假定预应力锚杆(索)和外围注浆体均为各向同性体,并在极小应力作用下处于弹性阶段,不计泊松比的影响[16]。考虑单位长度锚固体,由力的平衡条件、变形协调条件及材料的物理关系,可得
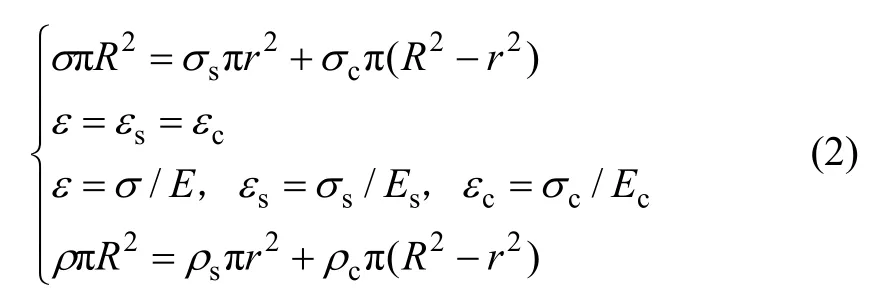
式中:E和ρ分别为锚固体的弹性模量和质量密度;σ,σs和σc分别锚固体、预应力锚杆(索)和外围注浆体所受的应力;ε,εs和εc分别为锚固体、预应力锚杆(索)和外围注浆体在其应力作用下的应变。由式(2)可得E和ρ为
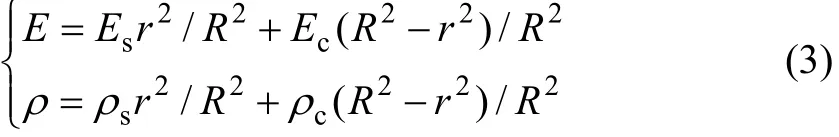
1.3锚固体断面变化处应力波的反射与透射
应力波在锚固体断面变化处发生反射和透射计算模型如图3所示。当应力波(图3中的波为右行波)从左向右传播时,若锚固体的断面发生变化(如由锚固体1变为锚固体2),则应力波将在其断面变化处MN发生应力波的反射和透射。设右行到界面MN处的入射波为I,反射波为R,透射波为T。对于锚固体1和2,其断面面积分别为A1和A2,弹性模量分别为E1和E2,质量密度分别为ρ1和ρ2。
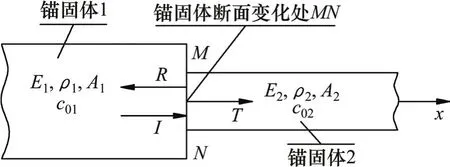
图3 应力波在锚固体断面变化处反射和透射计算模型Fig. 3 Calculation model of reflected and transmitted stress wave on changed cross-section of anchorage body
由锚固体在断面变化处的位移、速度和力的连续条件及一维应力波的波动方程[15]可得反射波、透射波与入射波的应力和速度关系式为

式中:σI,σR和σT分别为入射波、反射波和透射波的应力;vI,vR和vT分别为入射波、反射波和透射波的速度;α为阻抗,;c01和 c02分别为应力波在锚固体1和锚固体2中的传播速度。
1.4锚固体中应力波衰减规律
采用特征线法分析应力波在传播过程中的应力和速度时,并未考虑应力波能量随传播时间的增加而发生的衰减。为此,需要对特征线法所计算得应力波的应力和速度加以修正。
应力波对数衰减模型如图4所示。文献[17]通过研究一维弹性杆件应力波传播的波动方程,分析得出入射应力波的波速振幅衰减规律为对数衰减;文献[18]采用实验的方法研究了无黏结性钢绞线应力波波动振幅的衰减规律,并经最小二乘法对实验数据进行拟合,也得出入射应力波的波速振幅与其传播时间成对数衰减关系。本文假定应力波在锚固体中传播时其速度振幅与传播时间也呈对数衰减规律,即可假定v(t)=v0e−βt(其中,v0和v分别为修正前和修正后应力波的波速;t为应力波的传播时间;β为应力波衰减系数),文献[18]通过实验得到无黏结型钢绞线β在0.002~0.004之间,而一般钢材β值为1×10−4~ 6×10−4,本文将其取值为0~0.002,并研究应力波在锚固体中传播的衰减情况。
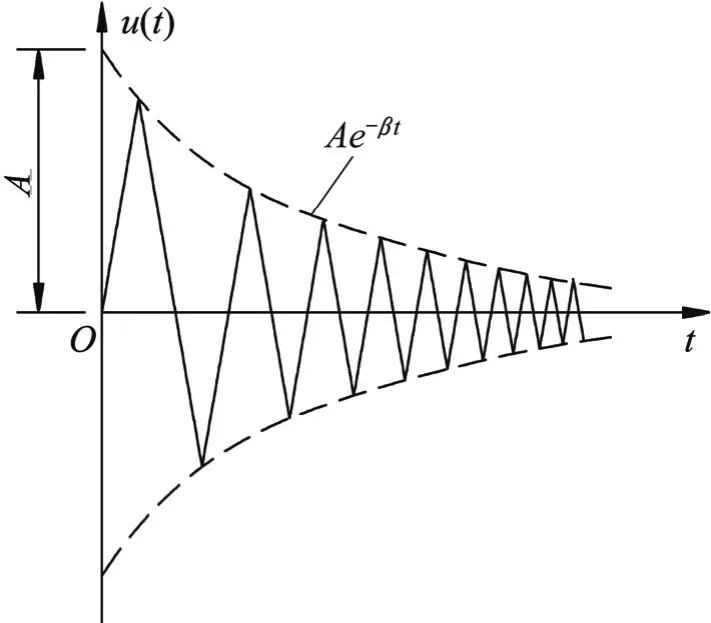
图4 应力波对数衰减模型Fig. 4 Logarithmic decay model of stress wave
2 几种特殊型式锚固体质量应力波检测方法
2.1均匀断面全长注浆型锚固体
均匀断面全长注浆型锚固体如图5所示。为便于考虑,以端头脉冲信号作用位置为原点,端头到底端方向为x轴正向,应力波沿特征线传播,锚杆(索)长度为L,锚固体的弹性模量为E1,质量密度为ρ1,断面面积为A1,应力波在其传播速度为c01;波段A1B1的应力波为脉冲信号作用在端头所得初始应力波,波段A2B2的应力波为脉冲信号作用在底端所得初始应力波。图5(a)中,波段CD的应力波为波段A1B1的应力波经锚固体底端反射后在端头接收到的应力波;图5(b)中,波段21的应力波为波段A2B2的应力波传播到端头所接收到的应力波。
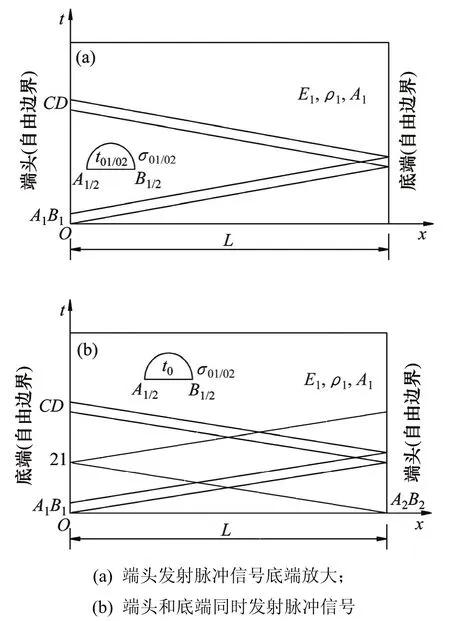
图5 均匀断面全长注浆型锚固体计算模型Fig. 5 Calculation model of full-length grouting anchorage body with uniform cross-section
在锚固体中传播的应力波满足如下初始条件:σ(x, 0)=0和v(x, 0)=0。其中,x的范围为0≤x≤L;当在端头(或底端)作用脉冲信号时,应力波满足σ(0, t)= σ01(0≤t≤t01时)和σ(L, t)=σ02(0≤t≤t02时)。设n为锚固体底端与端头脉冲信号的应力之比,即n=σ02/σ01。由以上条件并根据左特征线相容关系,可得波段A1B1的应力,速度,时间为(0,t01)。根据右特征线相容关系,可得波段A2B2的应力,速度,时间为(0, t02)。
对于端头发射脉冲信号底端放大方式的波段CD,可由波段A1B1的应力和速度,再根据右特征线相容关系与锚固体底端边界条件及左特征线相容关系与端头边界条件,并考虑应力波传播过程中呈对数螺旋衰减关系,可得其速度,时间为(2t1,t01+2t1)(其中,t1=L/c01,ω为底端信号放大比例系数)。
对于端头和底端同时发射脉冲信号方式的波段21,可由波段A2B2的应力和速度,再根据左特征线相容关系与锚固体端头边界条件,得其速度为,时间为(t1,t02+t1)。
2.2存在自由段非全长注浆型锚固体
存在自由段非全长注浆型锚固体如图6所示。为考虑方便,同样以端头脉冲信号作用位置为原点,端头到底端方向为x轴正向,应力波沿特征线传播,锚杆(索)长度为L,锚杆(索)自由段与锚固段交界面为MN(即锚固体断面变化处为MN)。锚杆(索)自由段长度为L1,弹性模量为E1,质量密度为ρ1,断面面积为A1,应力波在其传播速度为c01;锚固段长度为L2,弹性模量为E2,质量密度为ρ2,断面面积为A2,应力波在其传播速度为c02。同样,波段A1B1的应力波为脉冲信号作用在端头所得初始应力波,波段A2B2的应力波为脉冲信号作用在底端所得初始应力波。图6(a)中,波段11的应力波为波段A1B1的应力波经锚固体断面变化处MN反射后在端头接收到的应力波,波段CD的应力波为波段A1B1的应力波经底端发射后沿锚杆(索)自由段和锚固段传播到端头所接收到的应力波;图6(b)中,波段21的应力波为波段A2B2的应力波传播到端头所接收到的应力波;波段22的应力波为波段A2B2的应力波经锚固体断面变化处MN和底端各1次反射后沿锚固体和锚杆(索)自由段传播到端头所接收到的应力波。
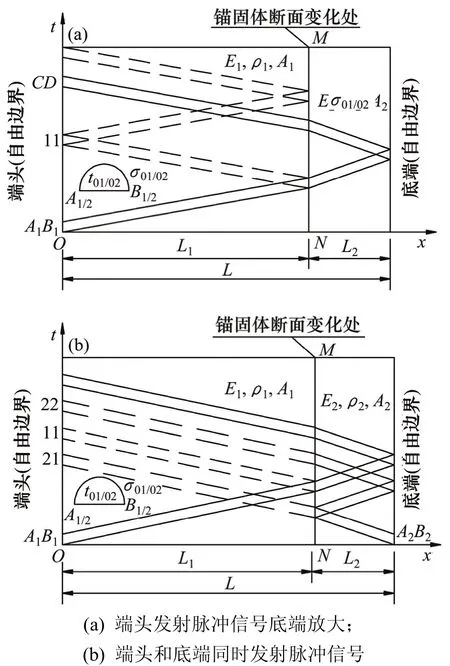
图6 存在自由段非全长注浆型锚固体计算模型Fig. 6 Calculation model of non-full-length grouting anchorage body with presence of free segment
本文考虑在锚固体端头接收的信号能够简便判断锚固体断面变化处的位置和锚杆(索)长度,对脉冲信号时间进行如下要求:
1) 当端头发射脉冲信号底端放大时(图6(a)),在波段A1B1和波段CD之间仅有1个由锚固体断面变化处MN反射回的波段11,且各波段之间不相互重叠,此时,脉冲信号时间t0需满足:t01<2(t1–t2)和t02<2t2(其中,t1=L1/c01,t2=L2/c02)。
2) 当端头和底端同时发射脉冲信号时(图6(b)),存在如下3种情况:情况一(t1>3t2),端头波段到达顺序为波段A1B1,21和22,则在波段12和波段56之间仅有1个波段34,脉冲信号时间t01和t02需满足:t01<t1+t2,t02<t1–3t2,t02<2(t1–t2),t02<2t2;情况二(t2<t1<3t2),端头波段到达顺序为波段A1B1,21和11,脉冲信号时间t01和t02需满足:t01<3t2–t1,t01<t1+t2,t02<t1–t2;情况三(t1<t2),端头波段到达顺序为波段A1B1,11和21,脉冲信号时间t01和t02需满足:t01<t2–t1,t01<2t1,t02<3t1–t2。
与前述计算一致,对于端头发射脉冲信号底端放大方式的波段11,可由波段A1B1的应力和速度,根据特征线相容关系、应力波在突变面传播规律和边界条件可得其速度,时间为(2t1,t01+2t1),其中,α=(A2E2/c02) / (A1E1/c01)。对于波段CD,可由波段A1B1的速度和应力,根据特征线相容关系、应力波在突变面传播规律和边界条件得其速度为,时间为(2t1+2t2, t01+2t1+2t2)(其中,ω为底端信号放大比例系数)。
与前述计算一致,对于端头和底端同时发射脉冲信号方式的波段21,可由波段A2B2的应力和速度,根据特征线相容关系、应力波在突变面传播规律和边界条件得其
2.3存在缺陷段全长注浆型锚固体
存在缺陷段全长注浆型锚固体如图7所示。为考虑方便,同样以端头脉冲信号作用位置为原点,端头到底端方向为x轴正向,应力波沿特征线传播,锚杆(索)长度为L,缺陷段与锚固段1交界面为M1N1(即锚固体断面变化处为M1N1),缺陷段与锚固段2交界面为M2N2(即锚固体断面变化处为M2N2)。锚固段1长度为L1,弹性模量为E1,质量密度为ρ1,断面面积为A1,应力波在其传播速度为c01;缺陷段长度为L2,弹性模量为E2,质量密度为ρ2,断面面积为A2,应力波在其传播速度为c02;锚固段2长度为L3,弹性模量为E3,质量密度为ρ3,断面面积为A3,应力波在其传播速度为c03。同样,波段A1B1的应力波为脉冲信号作用在端头所得初始应力波,波段A2B2的应力波为脉冲信号作用在底端所得初始应力波。图7(a)中,波段11的应力波为波段A1B1的应力波经锚固体断面变化处M1N1反射后在端头接收到的应力波,波段12的应力波为波段A1B1的应力波经锚固体断面变化处M2N2发射后沿缺陷段和锚固段1传播到端头所接收到的应力波,波段CD的应力波为波段A1B1的应力波经底端反射后沿锚固段2、缺陷段和锚固段1传播到端头所接收到的应力波;图7(b)中,波段21的应力波为波段A2B2的应力波传播到端头所接收到的应力波,波段22的应力波为波段A2B2的应力波经锚固体断面变化处M2N2和底端各反射1次后沿锚固段2、缺陷段和锚固段1传播到端头所接受到的应力波,波段23的应力波为波段A2B2的应力波经锚固体断面变化处M2N2和M1N1各反射1次后沿缺陷段和锚固段1传播到端头所接受到的应力波。

图7 存在缺陷段全长注浆型锚固体计算模型Fig. 7 Calculation model of full-length grouting anchorage body with present of defective segment
在此同样考虑在锚固体端头接收的信号能够简便判断缺陷段位置和锚杆(索)长度,对脉冲信号时间t0进行如下要求:
1) 当端头发射脉冲信号底端放大时(图7(a)),在波段A1B1和波段CD之间仅有1个由锚固体断面变化处M1N1和M2N2反射回的波段11和12,且各波段之间不相互重叠,此时,脉冲信号时间t0需满足:t0<2(t1–t2–t3),t0<2(t2–t3),t0<2t3(其中,t1=L1/c01,t2=L2/c02,t3=L3/c03)。
2) 当端头和底端同时发射脉冲信号时(图7(b)),由t2和t3的关系,脉冲信号时间t0需满足的条件见表1。
与前述计算一致,对于端头发射脉冲信号底端放大方式的波段11,可由波段A1B1的应力和速度,根据特征线相容关系、应力波在突变面传播规律和边界条件得其速度,时间为(2t1, t01+2t1)。其中,α1=(A2E2/c02)/(A1E1/c01)。对于波段12,可由波段A1B1的应力和速度,根据特征线相容关系、应力波在突变面传播规律和边界条件得其速度,时间为(2t1+2t2,t01+2t1+2t2),其中,α2=(A3E3/c03)/(A2E2/c02)。对于波段CD,由波段A1B1的应力和速度,及特征线相容关系、应力波在突变面传播规律和边界条件得其速度,时间为(2t1+2t2+2t3,t01+2t1+2t2+2t3)。
与前述计算一致,对于端头和底端同时发射脉冲信号方式的波段21,由波段A2B2的应力和速度,根据特征线相容关系、应力波在突变面传播规律和边界条件可得其速度,时间为(t1+t2+t3,t02+t1+t2+t3)。对于波段22,可由波段A2B2的应力和速度,根据特征线相容关系、应力波在突变面传播规律和边界条件得其速度v22=,时间为(t1+t2+3t3,t02+t1+t2+3t3)。对于波段23,可由波段A2B2的应力和速度,根据特征线相容关系、应力波在突变面传播规律和边界条件得其速度,时间为(t1+3t2+t3,t02+t1+3t2+t3)。
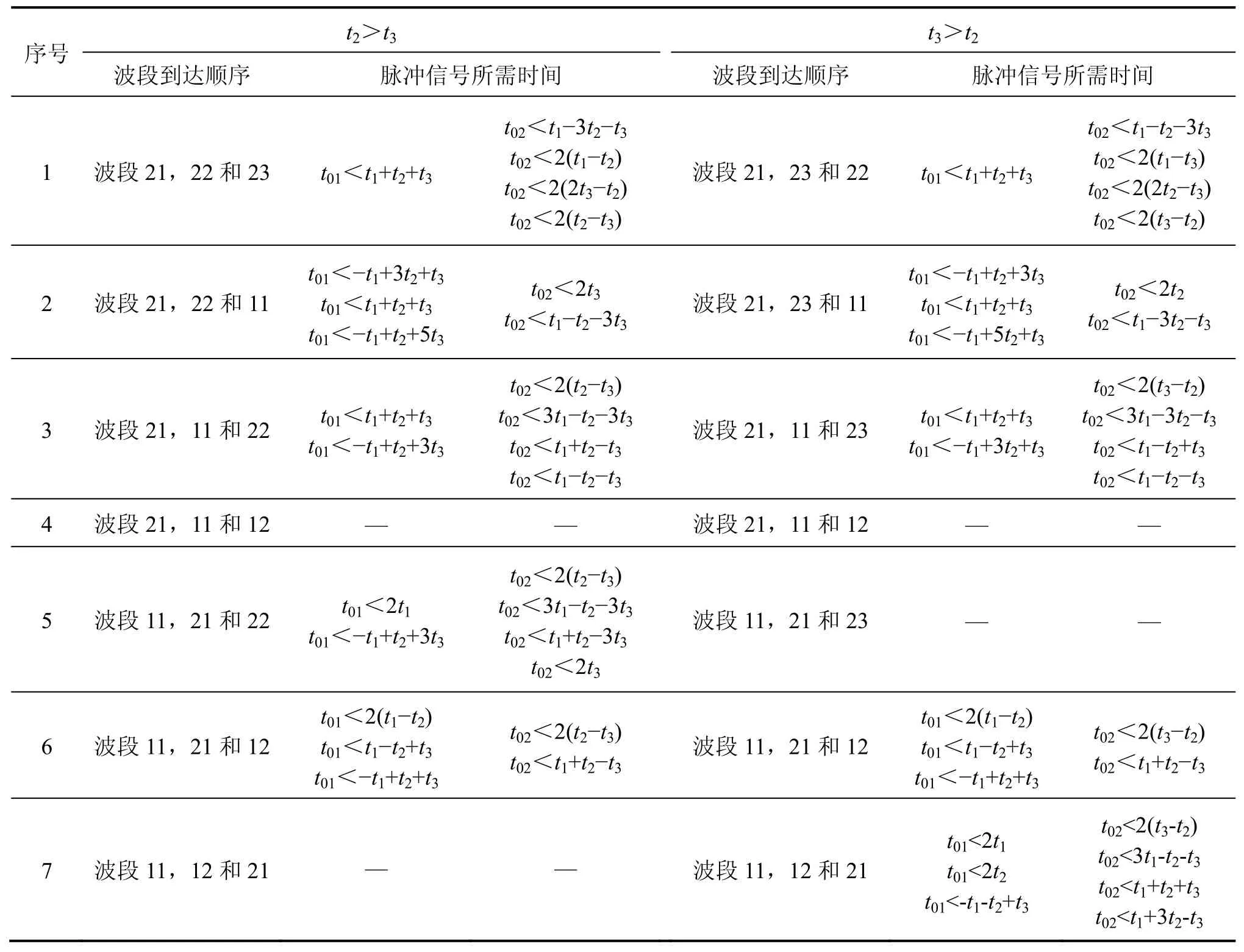
表1 端头和底端同时发射脉冲信号时简便判断锚固体质量所需脉冲信号时间Table 1 Pulse signal time required to easily detect quality of anchorage body when stress wave is launched simultaneously on its top and bottom
3 计算分析
在以下算例分析中,取预应力锚杆(索)长度L= 15 m,半径r=0.008 m,弹性模量Es=2.00×1011N/m2,质量密度ρs=7.8 t/m³;注浆体的弹性模量Ec按混凝土强度等级C15取值为2.20×1010N/m2,质量密度ρc= 2.4 t/m³。
3.1脉冲信号时间t0
算例1:当存在自由段非全长注浆型锚固体时(如图8(a)所示),取外围注浆体的外半径R = 0.058 m,研究不同自由段长度L1下2种信号增强方式(端头发射应力波信号底端放大与端头和底端同时发射应力波信号)在满足简便判别锚杆(索)长度及断面变化处位置所需的脉冲时间t0,其计算结果见表2。
算例2:当存在缺陷段全长注浆型锚固体时(如图8(b)所示),取锚固段1和锚固段2的外围注浆体的外半径R1=0.058 m,缺陷段外围注浆体的外半径R2按其饱满程度计算(,m为缺陷段注浆饱满度,单位为%),缺陷段长度L2=2 m。同样,研究锚固段1长度L1及不同缺陷段饱满度下2种信号增强方式(端头发射应力波信号底端放大与端头和底端同时发射应力波信号)在满足简便判别锚杆(索)长度及断面变化处位置所需的脉冲时间t0,其计算结果见表3。
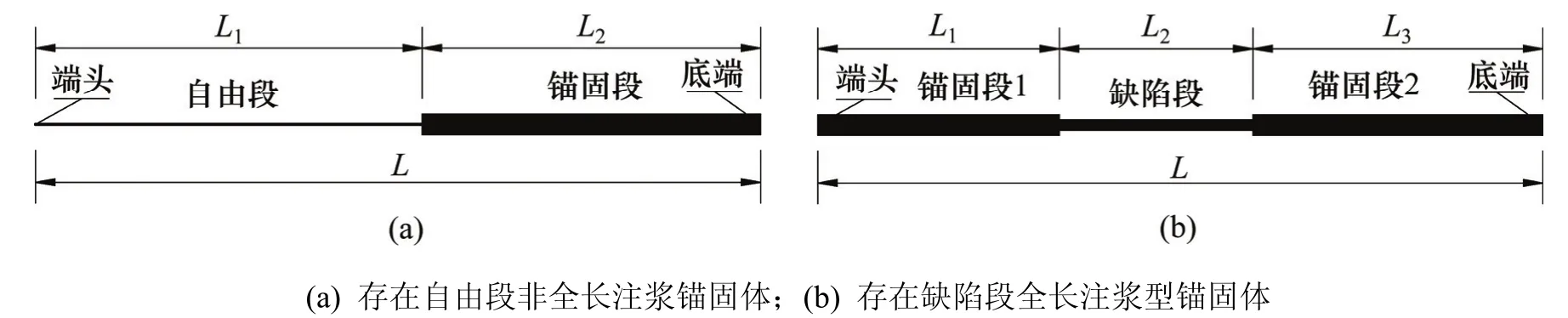
图8 非全长和全长注浆型锚固体计算模型Fig. 8 Calculation model of non-full-length and full-length grouting anchorage body

表2 算例1中简便判断锚固体质量脉冲信号所需时间Table 2 Pulse signal time required to detect easily quality of anchorage body in Example 1 s
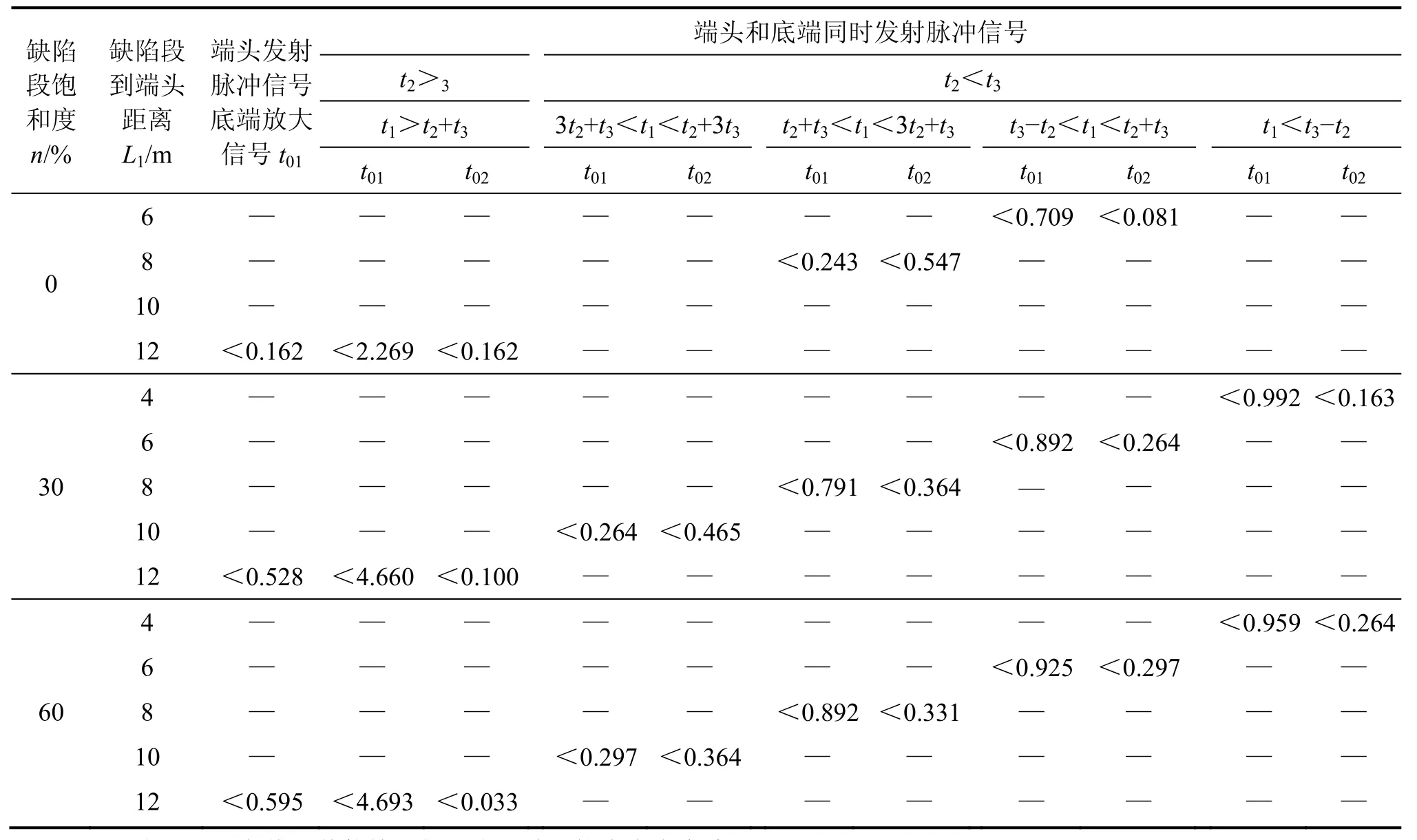
表3 算例2中简便判断锚固体质量脉冲信号所需时间Table 3 Pulse signal time required to detect easily quality of anchorage body in Example 2 s
由表2和表3可知:1) 对于端头和底端同时发射脉冲信号方式,仅在锚固体断面变化处位置离端头较近时(如存在自由段非全长注浆型锚固体的自由段长度L1为2 m和4 m,以及存在缺陷段全长注浆型锚固体的锚固段1长度L1为 2 m和4 m)不存在简便判断锚固体质量的脉冲信号时间,而对于端头发射脉冲信号底端放大方式,仅在锚固体断面变化处位置离端头较远时才存在有利于简便判断锚固体质量的脉冲信号时间,可说明端头和底端同时发射脉冲信号增强方式更利于工程应用;2) 由于判断锚固体质量只需从锚固体底端和断面位置变化处返回1次应力波信号,而对于端头和底端同时发射脉冲信号方式,当断面变化处的位置不同时在端头接受到的脉冲信号的顺序则并不一致,这在工程实际当中需进行分析,但在工程操作中可通过选择端头和底端发射脉冲信号频率的不同而区分在端头接受到的脉冲信号来自于端头反射还是底端透射(或反射)。
3.2算例分析
3.2.1均匀断面全长注浆型锚固体
算例3:取均匀断面全长注浆型锚固体其锚固体外围注浆体的外半径R=0.058 m,当锚固体中应力波衰减指数β从0变化到2.0×10−3(步长为0.2×10−3),研究锚固体底端信号放大比例系数ω和底端与端头应力波的应力之比n变化时,端头发射脉冲信号端头放大时波段CD相对波段A1B1振动速度绝对值的比例系数变化,及端头和底端同时发射脉冲信号时波段21相对波段A2B2振动速度绝对值的比例系数变化。计算结果表明:当底端信号放大系数ω与底端和端头脉冲信号的应力之比n相同时,对于在锚固体端头接受到经底端传播的应力波信号,端头和底端同时发射脉冲信号方式要强于底端发射脉冲信号底端放大方式。这主要是因为端头和底端同时发射脉冲信号方式在端头接受到经底端传播的应力波信号只需经过1倍锚杆(索)长度的时间,而端头发射脉冲信号底端放大方式在端头接受到经底端传播的应力波信号需经过2倍锚杆(索)长度的时间,故前者在端头接受到脉冲信号要较后者衰减得慢。
3.2.2存在自由段非全长注浆型锚固体
算例4:取存在自由段非全长注浆型锚固体其锚固段中锚固体外周注浆体的外半径R = 0.058 m,自由段长度为L1,锚固段长度为L2,研究锚固段长度L2变化和不同锚固体应力波衰减系数β下,端头发射脉冲信号底端放大时波段11,CD相对波段A1B1振动速度绝对值的比例系数变化(其中,底端放大比例系数ω=1),及端头和底端同时发射脉冲信号时波段21和11或22(当L2=2 m时波段22先于波段11到达端头时)相对波段A2B2振动速度绝对值的比例系数变化(其中,底端与端头应力波的应力之比n=1)。计算结果表明:对于存在自由段非全长注浆型锚固体,当ω=n=1时,在锚固体端头接受到经底端传播的脉冲信号,无论是未考虑应力波衰减还是在同一应力波衰减指数β下,端头和底端同时发射脉冲信号方式均强于端头发射脉冲信号底端放大方式,而在锚固体端头接受到经锚固体断面变化处(自由端和锚固段交界面)的脉冲信号,端头和底端同时发射脉冲信号方式与端头发射脉冲信号底端放大方式相同,这说明端头和底端同时发射脉冲信号方式是以锚固体端头接受到经底端或锚固体断面变化处的应力波信号传播时间为最短途径来有效对锚固体质量进行判断。
3.2.3存在缺陷段全长注浆型锚固体
算例5:存在缺陷段全长注浆型锚固体,其锚固段1和锚固段2(如图8(b)所示)中锚固体外围注浆体的外半径R=0.058 m,锚固段1(即缺陷段位置到端头的距离)L1=12 m,缺陷段长度L2=2 m,研究缺陷段注浆饱满度m为0~90%和在不同应力波衰减系数β下,2种应力波信号增加方式中各波段相对初始波段振动速度绝对值的比例系数变化(其中,底端放大比例系数ω=1,底端与端头应力波的应力之比n=1)。计算结果表明:1) 在锚固体端头接受到经端头和锚固体断面变化处的脉冲信号,仍为端头和底端同时发射脉冲信号方式强于端头发射脉冲信号底端放大方式,同样说明端头和底端同时发射脉冲信号方式更利于工程应用;2) 随着缺陷段饱和段的增加,在端头接受到经锚固体断面变化处的脉冲信号减弱,当缺陷段饱和度m为0~30%时,在端头接受到经锚固体断面变化处的脉冲信号基本变化不大,说明采用应力波法检测锚固体质量时仅能对缺陷段的饱和度进行定性分析。
4 结论
1) 对于端头和底端同时发射脉冲信号方式,除当锚固体断面变化处位置到端头的距离较小外,均存在适合简便判断锚固体质量(锚杆(索)长度和锚固体断面变化处位置)的脉冲信号时间;而对于端头发射脉冲信号底端放大方式,其适用范围则有较大的局限性,因而,端头和底端同时发射脉冲信号方式更适用于工程应用。
2) 采用端头和底端同时发射脉冲信号方式时,在锚固体端头接收到经底端或锚固体断面变化处的脉冲信号,均是反映锚杆(索)长度和锚固体断面变化处信息所需应力波的传播最短路径,故其所得的应力波信号要强于端头发射脉冲信号底端放大方式。
3) 当锚固体断面变化处位置不相同时,采用端头和底端同时发射脉冲信号方式在锚固体端头接收到的经底端和锚固体断面位置变化处的脉冲信号到达顺序并不一致,故在实际操作中,需对端头和底端的脉冲信号采用不同频率加以区分。
[1] 孙冰, 曾晟, 丁德馨, 等. 低应变动测桩及锚杆中波的传播规律差异研究[J]. 岩土力学, 2011, 32(4): 1143−1148. SUN Bing, ZENG Sheng, DING Dexin, et al. Research on transmit rules of stress wave with low strain in dynamic test pile and anchorage bolt[J]. Rock and Soil Mechanics, 2011, 32(4): 1143−1148.
[2] 寇林田, 吴剑, 薛泽峰, 等. 隧道锚杆锚固质量的应力波检测技术研究[J]. 地下空间与工程学报, 2010, 6(2): 391−395. KOU Lintian, WU Jian, XUE Zefeng, et al. Study on stress wave detection technology of tunnel anchor quality[J]. Chinese Journal of Underground Space and Engineering, 2010, 6(2): 391−395.
[3] 李志辉, 李亮, 李建生. 应力波法锚杆无损检测技术研究[J].测绘科学, 2009, 34(1): 205−206. LI Zhihui, LI Liang, LI Jiansheng. Research on stress wave method for bolt nondestructive testing technique[J]. Science of Surveying and Mapping, 2009, 34(1): 205−206.
[4] 曾辉辉, 王立伟, 朱本珍, 等. 应力波法在黏结型锚索质量检测中的应用研究[J]. 铁道建筑, 2011, 51(6): 96−98. ZENG Huihui, WANG Liwei, ZHU Benzhen, et al. The application of stress wave method on detecting quality of bond-type anchor cable[J]. Railway Engineering, 2011, 51(6): 96−98.
[5] WANG Mingwu, WANG Heling. Nondestructive testing of grouted bolts system[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(1): 109−113.
[6] 许明. 锚固系统质量的无损检测与智能诊断技术研究[D]. 重庆: 重庆大学土木工程学院, 2002: 21−64. XU Ming. A study on nondestructive detection and intelligent diagnosis technology of anchorage system quality[D]. Chongqing: Chongqing University. College of Civil Engineering, 2002: 21−64.
[7] 江杰. 应力波法锚杆加固无损检测与锚固效果评价的研究[D].武汉: 武汉理工大学土木工程与建筑学院, 2005: 12−15. JIANG Jie. A study on non-destructive detection of stress wave in anchorage bolts and evaluation of anchorage system quality[D]. Wuhan: Wuhan University of Technology. College of Civil Engineering and Architecture, 2005: 12−15.
[8] 张献民, 蔡靖, 王建华. 桩基缺陷量化低应变动测研究[J]. 岩土工程学报, 2003, 25(1): 47−50. ZHANG Xianmin, CAI Jing, WANG Jianhua. Quantitative analysis of defects of piles in foundation with low strain dynamic test[J]. Chinese Journal of Geotechnical Engineering, 2003, 25(1): 47−50.
[9] Likins G E, Rausche F. Recent advances and proper use of PDI low strain pile integrity testing[C]// Proceedings of Sixth International Conference on the Application of Stress-wave Theory to Piles.St. Paulo, Brazil, 2000: 211−218.
[10] 陈建功, 胡俊强, 张永兴. 基于完整锚杆动测技术的围岩质量识别研究[J]. 岩土力学, 2009, 30(6): 1799−1804. CHEN Jiangong, HU Junqiang, ZHANG Yongxing. Identification of surrounding rock quality based on dynamic testing technology of integrated anchor[J]. Rock and Soil Mechanics, 2009, 30(6): 1799−1804.
[11] 杨天春, 吴燕清, 夏代林. 基于相位推算法的锚杆施工质量无损检测分析方法[J]. 煤炭学报, 2009, 34(5): 629−633. YANG Tianchun, WU Yanqing, XIA Dailin. An analytic method for rock bolts non-destructive testing signals by phase deducted method[J]. Journal of China Coal Society, 2009, 34(5): 629−633.
[12] 万世文, 徐金海, 吴锐. 预应力锚杆弹性波检测的激振波及其传播规律研究[J]. 采矿与安全工程学报, 2011, 28(4): 581−584. WAN Shiwen, XU Jinhai, WU Ru. Study on the exciting wave and its propagation rules of elastic wave testing on pre-stressed anchor[J]. Journal of Mining and Safety Engineering, 2011, 28(4): 581−584.
[13] 李义, 王成. 应力反射波法检测锚杆锚固质量的实验研究[J].煤炭学报, 2000, 25(2): 160−164. LI Yi, WANG Cheng. Experiment study on bolt bonding integrity with stress reflected wave method[J]. Journal of China Coal Society, 2000, 25(2): 160−164.
[14] 刘海峰, 杨维武, 李义. 全长锚固锚杆早期锚固质量无损检测技术[J]. 煤炭学报, 2007, 32(10): 1066−1069. LIU Haifeng, YANG Weiwu, LI Yi. Non-destructive technology of all-lengthy anchorage rock bolt at early age[J]. Journal of China Coal Society, 2007, 32(10): 1066−1069.
[15] 马宏伟, 吴斌. 弹性动力学及其数值方法[M]. 北京: 中国建材工业出版社, 2000: 12−36. MA Hongwei, WU Bin. Elastic dynamics and its numerical method[M]. Beijing: China Building Materials Industry Press, 2000: 12−36.
[16] 李新平, 江杰, 鲁志鹏, 等. 应力波法锚杆加固无损检测的数值模拟分析研究[J]. 岩石力学与工程学报, 2005, 24(增1): 4647−4652. LI Xinping, JIANG Jie, LU Zhipeng, et al. Numerical simulation analysis of nondestructive detection of stress wave in anchorage bolts[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(S1): 4647−4652.
[17] 张方胜, 何沛祥. 低应变动测桩身应力波衰减规律及其应用[J]. 合肥工业大学学报(自然科学版), 2008, 31(6): 942−945. ZHANG Fangsheng, HE Peixiang. Attenuation principle of stress wave in low strain dynamic test and its application[J]. Journal of Hefei University of technology (Natural Science Edition), 2008, 31(6): 942−945.
[18] 梁龙龙. 应力波法在边坡预应力锚索(无黏结型)结构检测中的试验研究[D]. 北京: 铁道科学研究院, 2007: 25−61. LIANG Longlong. A study on stress wave method in pre-stressed (non-bonded) anchor cable structure detection of slope[D]. Beijing: Academy of Railway Sciences, 2007: 25−61.
(编辑 陈灿华)
Applicability of two stress wave signal enhancement modes in anchorage quality testing of pre-stressed anchor (cable)
DENG Dongping, LI Liang, ZHAO Lianheng
(School of Civil Engineering, Central South University, Changsha 410075, China)
With the growth of anchor (cable) length, the logarithmic spiral attenuation with time in dissemination process. Meanwhile, feature line method was used to calculate stress wave signal time during which the anchor body quality could be judged easily, and to calculate the velocity of
stress wave on the top of anchorage body from the bottom and changed cross-section of anchorage body. Some examples including three special types of anchorage body (full-length grouting with uniform cross-section, non-full-length grouting type with free segment, and full-length grouting with defective segment) were studied. The results show that except that the position of changed cross-section is closer to the top of anchor body, there is pulse signal time to easily judge the quality of anchor body for the second kind of signal enhancement mode. However, there is pulse signal time to easily judge the quality of anchor body only in case that the position of changed cross-section is farther to the top of anchor body for the first kind of signal enhancement mode. When the second kind of signal enhancement mode is used, the
pulse signals that can reflect information of anchor (cable) length and position of changed cross-section on top of anchorage body are signals that last the shortest time to reach the top from the bottom and changed cross-section, and so strength of the collected pulse signal by the second kind is better than that by the first kind. As there is a pair of opposing spread stress wave signal in the second kind of signal enhancement mode and each signal can reflect information of quality of anchorage body, so the emitted stress wave signal on the top and bottom of anchorage body needs different frequencies to distinguish the above-mentioned information.
pulse signal used to judge the quality of anchorage body (length of anchor (cable) and position of changed cross-section of anchorage body) on its top is weaker, and so the
pulse signal on the top of anchorage body should be strengthened so that stress wave method is also applied to detect the anchorage quality of longer anchor (cable).Two kinds of stress wave signal enhancement modes are selected as follows: pulse signal was transmitted on the top of anchorage body and amplified on its bottom; and pulse signals were transmitted simultaneously on the top and bottom of anchorage body. Then propagation velocity of stress wave was calculated by adopting complex body consisting of anchor (cable) and grouting body and stress wave displayed
pre-stressed anchor (cable); stress wave; feature line method; anchorage body; pulse time; excitation mode
TU45
A
1672−7207(2016)03−0936−10
10.11817/j.issn.1672-7207.2016.03.029
2015−04−10;
2015−08−08
教育部博士研究生学术新人奖项目(114801045);湖南省研究生科研创新项目(CX2012B056) ;贵州省交通运输厅科技项目(2010-122-020) (Project(114801045) supported by the Ph.D Scholarship Award of Ministry of Education; Project(CX2012B056) supported by the Graduate Student Research Innovation of Hunan Province; Project(2010-122-020) supported by Transportation Department of Guizhou Province)
邓东平,博士(后),从事道路与铁道工程等研究;E-mail: dengdp851112@126.com
