应用边界元法分析页岩地层井眼坍塌问题

马天寿，陈平

(西南石油大学 油气藏地质及开发工程国家重点实验室，四川 成都，610500)

应用边界元法分析页岩地层井眼坍塌问题

马天寿，陈平

(西南石油大学 油气藏地质及开发工程国家重点实验室，四川 成都，610500)

基于各向异性连续介质力学和边界元理论，建立横观各向同性页岩地层井眼坍塌定问题的基本微分方程，推导出基本方程的边界积分方程及其离散解，并得出井周应力和位移的边界元离散解，结合Mohr−Coulomb准则判别井眼稳定性，形成基于边界元法(BEM)求解井眼坍塌问题的基本方法。建立页岩地层井眼坍塌问题的物理模型，采用各向同性地层模型对BEM进行检验，并开展井周应力分布规律研究和应用实例分析。研究结果表明：BEM求解结果与解析解吻合较好，二者相对误差小于2.49%；弹性模量各向异性、水平地应力差异和钻井液密度等对井壁应力分布影响较大(其中水平地应力差异的影响最大)，而泊松比各向异性的影响较小；W201井1 530 m井段井眼稳定性分析结果与电测结果吻合良好，BEM计算的扩径率约为9.0%，而电测扩径率约为10.0%。

页岩；井眼稳定；横观各向同性；边界元(BEM)；数值方法

页岩气是以富有机质页岩为气源岩、储层或盖层，在页岩地层中不间断供气、连续聚集而形成的一种非常规天然气，存在于几乎所有的盆地中，由于埋藏深度、含气饱和度等差异较大，分别具有不同的工业价值[1−2]。通过多年的努力，美国取得页岩气勘探开发技术突破，近10 a产量快速增长，美国已超过俄罗斯成为全球最大的天然气生产国，由天然气净进口国转变为净出口国。受美国页岩气成功开发的启示，我国页岩气开发也已成为了业界的焦点问题，并开展了页岩气勘探评价和先导试验[1]。在中石油在四川南部的长宁—威远国家级页岩气示范区、壳牌和中石油合作的云南昭通国家级页岩气示范区以及中石化在重庆东部礁石坝构造的钻探试采结果表明，页岩地层钻井过程中井眼垮塌较严重，导致卡钻、埋钻等井下复杂和事故频频发生[1−2]。减少井下复杂和事故发生的关键在于提高页岩地层井眼的稳定性，这使页岩井眼稳定问题成为页岩气高效开发的关键问题之一[3]。针对页岩地层井眼稳定问题的研究，国内外已经开展了大量研究并取得了较丰富的成果[4]，已经形成多种井眼稳定的计算和分析方法，如解析解方法、有限元方法(FEM)、离散元方法(DEM)、其他数值计算方法等。解析解方法为最早出现的井眼稳定分析方法之一，WESTERGARD[5]把柱坐标引入井眼坐标系中，利用应力函数计算井眼弹塑性问题，初步研究了井壁稳定机理，并对现场实例和处理方法进行了讨论，直接推动井眼稳定问题进入定量化研究阶段；此后逐渐形成了一系列以线弹性力学、孔隙弹性力学、弹塑性力学为基础的井壁稳定力学计算方法，由于这些方法计算简便，且可得出沿井深的井眼坍塌、破裂压力剖面，因而被广泛采用。然而，解析解方法假设条件过多，计算结果往往存在较大的误差。随着有限元理论的快速发展，FEM开始被用于分析井眼稳定问题，FEM主要被用于井眼稳定弹塑性分析和多场耦合分析；考虑到井眼稳定问题的对称性，大量学者将其简化为广义平面应变问题进行求解[6−10]，也有一些学者直接采用三维有限元模型求解分析[11−12]；FEM计算灵活性较高、可处理应力集中和非线性问题；但FEM经常会出现网格划分困难、矩阵运算量过大、计算内存大、计算较慢等问题。DEM是一种非连续介质力学分析方法[13−15]，因此，DEM主要适用于分析节理、破碎性地层的井眼稳定问题。有限差分方法(FDM)[16−18]计算简单，但不适用于不规则物体，也不能处理应力集中问题。真实破裂过程分析方法(RFPA)[19]为一种基于统计损伤力学的方法，在工程应用中其基础参数获取困难。不难看出，这些方法仍存在一些难以解决的问题。WANG等[20−21]采用边界元方法(BEM)研究了井漏中的裂缝延伸问题，指出BEM对边界积分方程离散求解的现代数值分析方法，属于近似求解方法之一，BEM适合于求解无穷域或应力集中问题，具有降阶、降维的特点[22−23]，其优点在于依靠微分方程阶数的减少以降低对近似试函数所必需的可导阶数[23]。因此，BEM方法所得控制方程为积分方程，该方法降低了计算维度，主要考虑物体边界(边界单元处理容易)，其计算精度较高、内存小、速度快，目前采用BEM方法研究井眼坍塌问题的文献鲜见报道。因此，本文作者引入BEM方法来分析井眼坍塌问题，通过分析横观各向同性页岩地层的BEM求解方法和求解结果，阐述BEM在井眼稳定问题分析中的应用，借此将BEM引入到井眼稳定分析方法中，从而为井眼稳定问题的分析提供更多有力的手段和方法。

1　页岩井眼稳定问题分析方法

1.1数学模型

页岩的典型特点是层理、微裂隙发育，层理性地层是指有一组近于平行的层理面，层理的强度明显比岩石本体强度低很多，CHENEVERT等[24]通过实验证实当层理面法线与最大主应力夹角为20º～30º时，其强度比垂直于层理面方向取心降低40%左右。层理性页岩与横观各向同性材料具有极强的相似性，在层理面内各方向的性质基本相同，而在层理面法线方向性质不同，因此，可以将页岩地层视为横观各向同性材料，并给出相应的数学模型。

平衡方程为

几何方程为

横观各向同性页岩的本构方程[23]

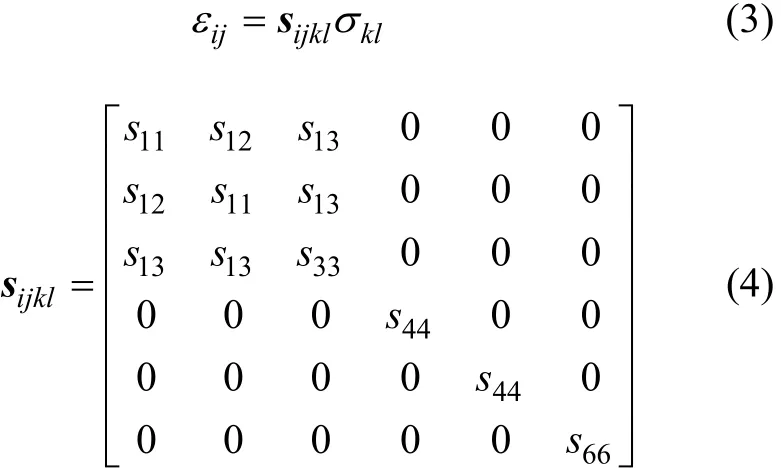
式中：σij为总应力；xj为坐标轴；fi为体力；εij为应变分量；ui为位移；sijkl为柔度矩阵；i，j，k和l为循环角标。

式中：E和E′为平行和垂直横观各向同性面的弹性模量；v和v′为平行和垂直横观各向同性面的泊松比。

若假设井眼轴线方向为z轴，则井眼平面横截面面积和形状沿z轴不发生改变，作用的外力与z轴垂直，则井周地层的位移将主要发生在横截面内，因此，往往将其简化为广义的平面应变问题。于是，在Oxyz直角坐标系中所有的应变分量均与z方向无关[25]，即

将式(3)代入式(6)可得

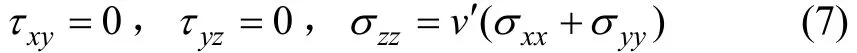
再将式(7)代入式(3)，可得平面应变问题本构方程

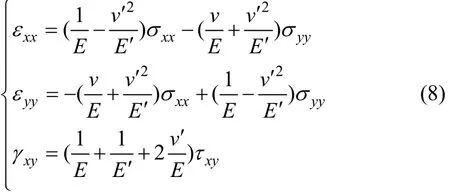
式中：σxx，σyy，σzz，τxy，τyz和τxz为应力分量；εxx，εyy，εzz，γxy，γyz和γxz为应变分量。

在Γ1上，静力边界条件为

在Γ2上，位移边界条件为

式中：pi为边界应力；为边界上给定的应力分量，上方记号“”表示该值已知，下同；ui为边界位移；为边界上给定的位移分量；Γ1和Γ2为边界。

将式(2)代入式(8)中，再将得到的结果代入式(1)中，即可得到由位移表示的应力平衡方程，即本文求解的基本方程。

1.2边界元求解方法

为了求解横观各向同性页岩地层井眼稳定问题的基本方程，首先要将基本方程转化为边界积分方程。但横观各向同性材料基本解的数学描述较复杂，为此，采用一种适用于任一各向异性材料的方法，即参照各向同性材料基本解并以迭代法逼近正确解[22]。若忽略体力，则基本微分方程的加权余量表达式为

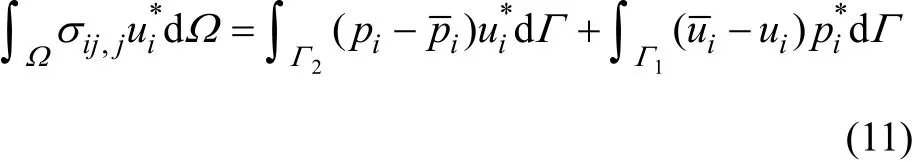
若考虑采用参照弹性模型的各向同性材料基本解，此参照弹性模型是以各向异性材料常数的平均值建立的。因此，原有弹性常数张量dijkl[22]表示为

式中：dijkl为实际弹性常数；为参照态弹性常数；为实际与参照态弹性常数的差值。因此，本构方程可表示为

将式(11)进行分部积分得

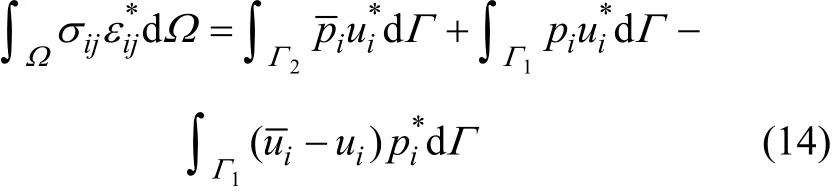
将式(13)代入式(14)，并将式(15)带入，进行分部积分后可得

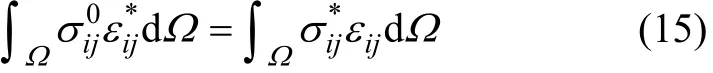
由于基本解同时满足域内和边界，将式(16)针对边界上的力作用点m，可改写为

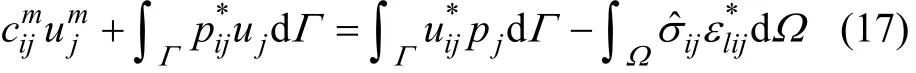
式(17)中不仅出现了边界积分项，还出现了域积分项，可将域积分项变换成体力项和边界积分项[22]再计算。对式(17)右端第2项采用分部积分可得

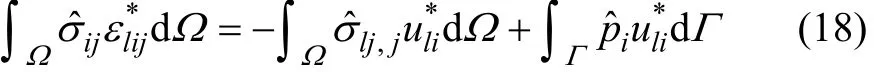
式(18)中右端第一项可等效处理为体力项，即

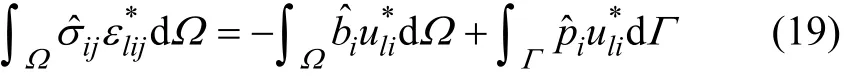
将式(19)代入式(17)可得

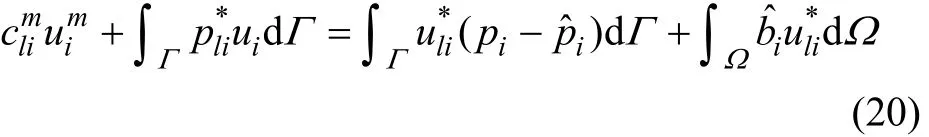
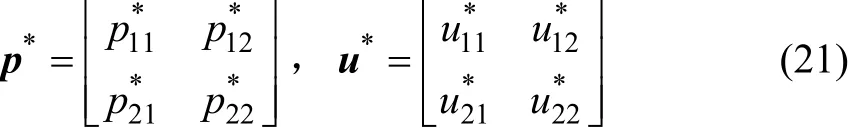
将平面问题位移、表面力、等效面力和等效体力矢量可表示为

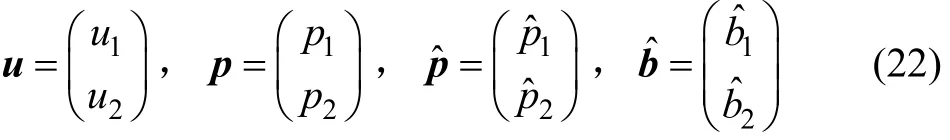
为了将边界积分方程离散化，采用常单元分割求解域及边界，则u和p在单元内是常量，等于单元中点(节点)的值。则式(20)可写成离散形式，即

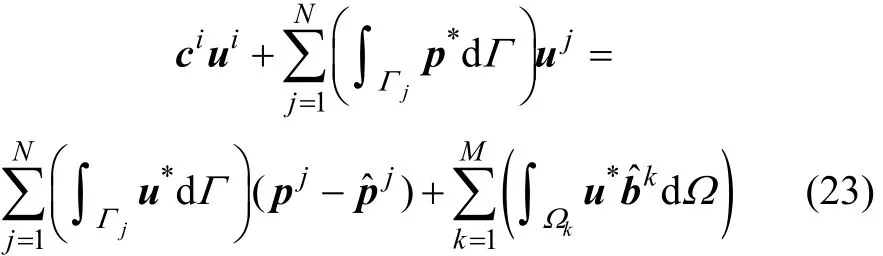
式中：ui为基本解多用点i(边界或域内)的位移；ci为2×2阶的常数矩阵，取决于该节点i所在的位置及几何形状；为与i节点和j节点有关的边界积分项，称为影响系数[22]，经过积分计算后成为2×2阶的矩阵和Gij。

而等效体力项的数值积分需按下式计算

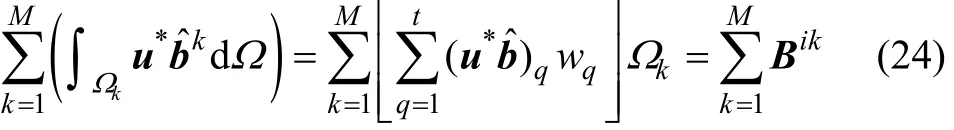
式中：wq为权函数；Ωk为域元面积。数值积分计算后得到Bik的2个分量。函数在积分节点q上计算，q的取值为1～t。

据此，将式(24)代入式(23)可得

若令

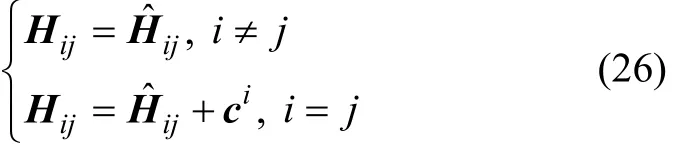
则式(25)可写成

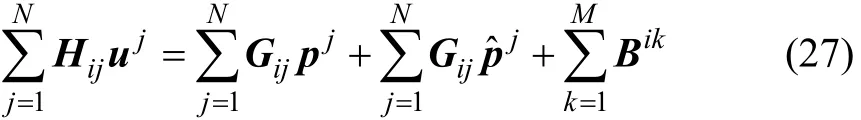
对边界上所有节点应用式(27)，可得矩阵方程

式中：H和G均为2N×2N阶的矩阵，N为边界上的节点总数；B为体力项列向量。

将已知边界条件代入式(28)，并将未知量及其系数移至方程的左边，其余项移至方程的右边可得

式中：A为与H和G相关的矩阵；x为未知数组，包括位移和面力；F为已知边界条件和对应H和G相乘所得的列向量。

求解式(29)可以获得全部边值。当获得全部边界值(位移和表面力)后，便可计算域内任一点的位移和应力。为了得到求解域内的位移分布，可采用Somigliana公式求解[22,25]，将Somigliana公式表示的边界积分方程写成离散形式：

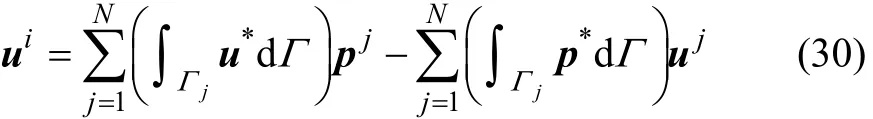
为了得到求解域内点的应力分布，可通过对该点位移的求导和本构方程加以确定，求得域内点应力分布的边界积分方程离散形式[22,25]为

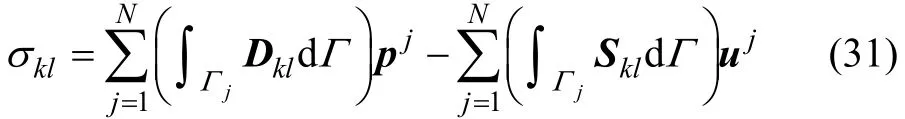
其中：Dkl和Skl为系数矩阵；Dkij和Skij为与边界条件有关的系数；δij为克罗内克函数；r为矢径长度。

式(31)即为采用BEM方法求解井眼周围应力分布的方法，通过BEM计算得出井周应力分布后，结合强度判别准则即可进行井眼稳定性分析，本文采用Mohr−Coulomb准则进行井眼稳定性分析。

1.3强度判别准则

在进行井眼稳定性判别前，需要将广义平面二向应力状态结果转换为空间主应力状态，即计算出空间应力状态下的主应力。采用BEM求解得到的应力张量σ为

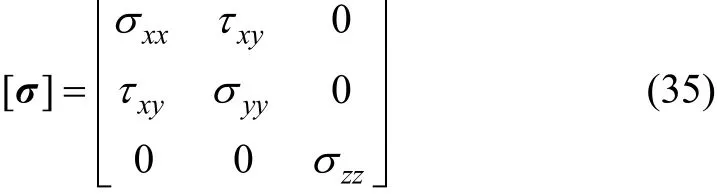
因此，井眼局部圆柱坐标系下空间主应力为：

式中：1σ和3σ分别井周地层的最大和最小主应力；γ为井壁最大主应力与井眼轴线之间的夹角。

获得层理性页岩井周最大、最小主应力后，代入强度准则(Mohr−Coulomb准则)，即可进行稳定性判别，Mohr−Coulomb准则可表示为

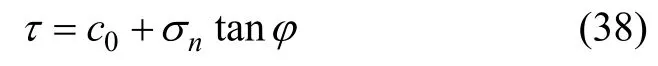
当采用Mohr−Coulomb准则判别井眼不稳定时，假设页岩地层强度系数(strength factor，FS)为

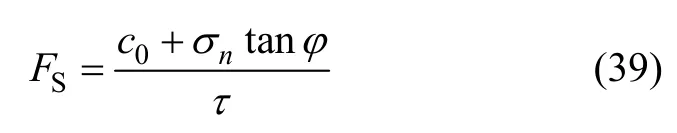
当FS＞1时，井周页岩地层稳定；当FS＜1时，井周页岩地层将发生失稳。因此，FS越小，则表示井眼失稳的风险越大。

若将最大主应力σ1和最小主应力σ3代入式(38)，可得Mohr−Coulomb准则的另一种表达形式为

式中：τ为剪切面上剪应力；σn为剪切面上正应力；c0为岩石内聚力；ϕ为岩石内摩擦角；pp为地层孔隙压力；α为Biot系数。

2　边界元求解模型的建立与验证

2.1求解模型的建立

对于页岩地层中所钻的井眼来说，沿轴向方向的应变可近似认为是一常量，即可将复杂的三维空间应力分析问题转化为广义平面应变问题来考虑。因此，当采用BEM求解时，所建立的井周地层计算网络模型如图1所示，分别为求解域计算网络模型与井壁周围离散后的计算网络模型局部视图，本文后续分析均采用这种计算网络模型，图1(b)中的a→b→c→d→a为应力分布取值路径。在后续计算和分析中，所采用的基础参数如表1所示。

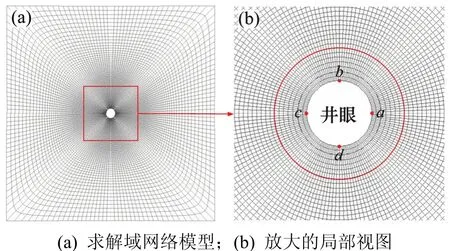
图1　井周地层计算网络模型Fig. 1 Mesh model of formation around borehole

表1　井周地层计算基础参数Table 1 Basic parameters of formation around borehole

2.2模型验证

为了检验本文模型的准确性，取各向同性均质地层直井井眼模型来检验BEM的准确性，分别采用常规井壁稳定力学分析方法(解析解)[4]和BEM计算井周应力分布情况。此时，取各向异性系数为1.0(即nE=E′/E=1.0，nυ=υ′/υ=1.0)，其他基础参数如表1所示。首先，采用BEM计算出各向同性均质地层井周应力分布情况，提取出一倍井眼范围内的井周应力分布，结果如图2所示。为了对比解析解方法和BEM计算结果，取井壁处a→b→c→d→a路径的应力(径向应力rσ、切向应力θσ、轴向应力zσ)计算结果进行对比，如图3所示。

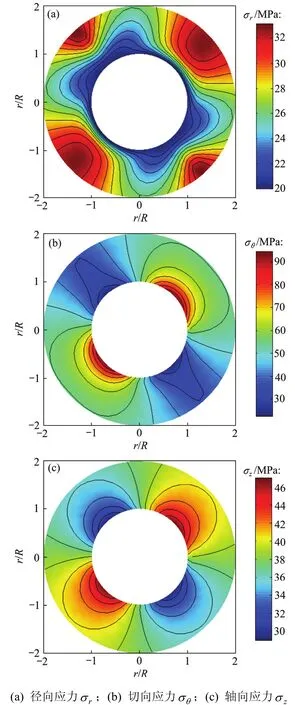
图2　边界元方法解出的井周应力分布图Fig. 2 Stress distribution of wellbore by BEM

图3　井壁(r=R)应力分布图Fig. 3 Stress distribution of borehole wall (r=R)

由图3可以看出，井周应力分布的求解结果在径向、切向和轴向(z轴)3个方向的计算结果均吻合较好，BEM计算结果与解析解计算结果之间的相对误差小于2.49%。另外，井周应力分布在最小水平地应力方向上的应力差异最大(井壁切向应力远高于径向应力)，在最大水平地应力方向上的差异较小(井壁切向、轴向和径向应力十分接近)，使各向同性地层中井眼坍塌通常发生在最小水平地应力方向上。对于二者计算误差，主要原因是由于BEM是一种近似求解的数值方法，加之划分网格单元的不规则性，使其计算结果与解析解计算结果有些差异，但总体上误差较小，能够满足工程所需精度，验证了BEM的正确性和准确性。

3　计算结果讨论

3.1弹性模量对井壁应力的影响

定义横观各向同性页岩地层弹性模量各向异性系数nE=E′/E，则nE表征了页岩地层岩石的各向异性程度，其值越小表示各向异性程度越高，nE=1表示各向同性，通过计算得到图4所示的结果。

由图4可见：页岩地层井壁切向应力分布规律近似“哑铃”状，nE对井壁切向应力的影响比较显著；各向异性程度越高(nE越小)，对井壁切向应力分布的影响越大，井壁切向应力分布由规则“哑铃”状逐渐变成不规则形状；在不同各向异性程度的地层中，井壁切向应力的极大值和极小值不同，各向异性程度越高则井壁切向应力极值越高(如nE=0.25时切向应力极值为97.68 MPa，而各向同性地层为94.32 MPa)，且切向应力极小值也越小；井壁切向应力分布规律还与井周角和地应力方位有关，井壁切向应力极大值点在最小水平地应力方向附近，随着各向异性程度增加，应力极大值点开始向最大水平地应力方向偏转。

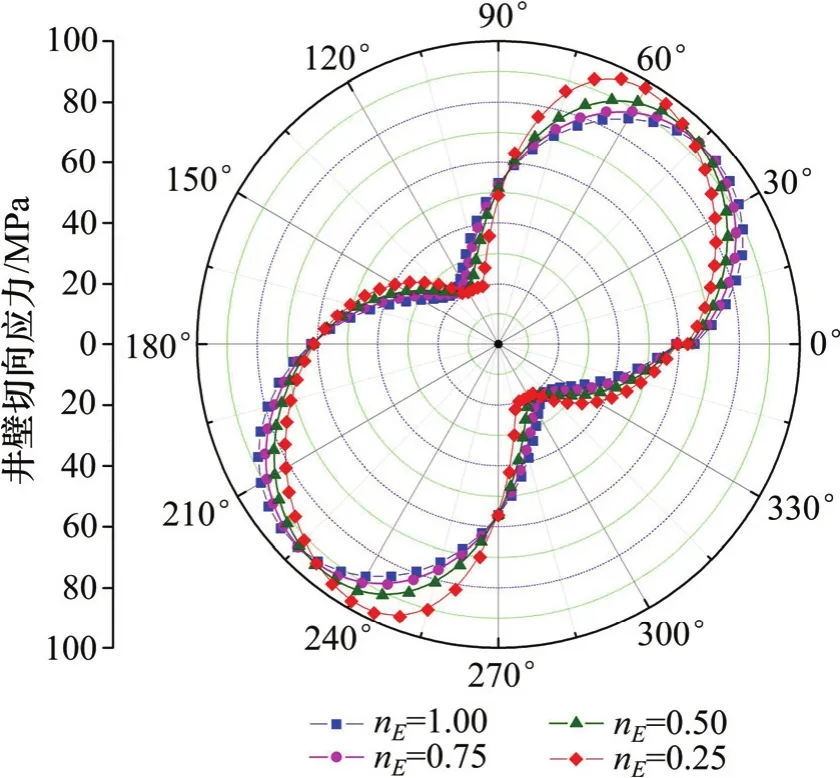
图4　nE对井壁切向应力分布的影响Fig. 4 Influence of nEon tangential stress distribution at borehole wall

3.2泊松比对井壁应力的影响

定义横观各向同性页岩地层泊松比各向异性系数nυ=υ′/υ，则nυ为页岩地层岩石的各向异性程度，其值越小表示各向异性程度越高，nυ=1为各向同性，通过计算得图5所示的结果。由图5可以看出：页岩地层井壁切向应力分布规律近似“哑铃”状，nυ对井壁切向应力几乎没有影响；井壁切向应力极大值约为94.32 MPa，其位于最小水平地应力方向；井壁切向应力极小值约为22.43 MPa，其位于最大水平地应力方向。

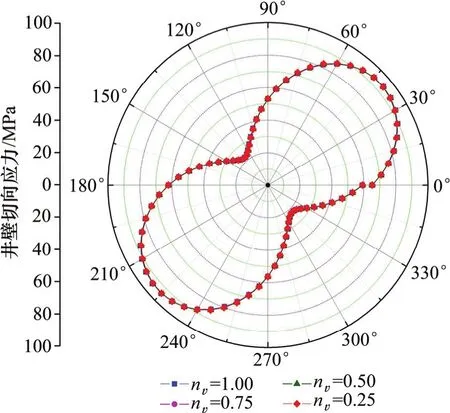
图5　nυ对井壁切向应力分布的影响Fig. 5 Influence of nυon tangential stress distribution at borehole wall

3.3地应力对井壁应力的影响

定义页岩地层水平地应力比mσ=σh/σH，为此，可固定最大水平地应力σH，取水平地应力比mσ=0.25，0.50，0.75，1.00共4种情况分别计算，以研究地应力对井壁应力分布的影响。考虑到泊松比各向异性对井壁应力分布的影响较小，弹性模量各向异性对井壁应力分布的影响较大，此处分别计算了在nE为0.25和1.00这2种情况下，不同地应力比下的井壁应力分布情况，其结果如图6所示。

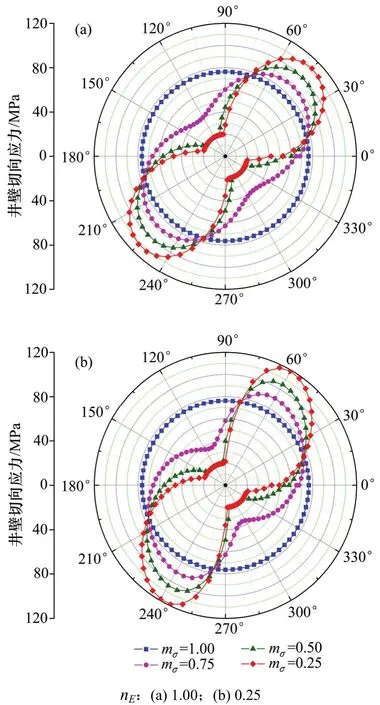
图6　水平地应力比mσ对井壁切向应力分布的影响Fig. 6 Influence of ratio of horizontal in-situ stress (mσ) on tangential stress distribution at borehole wall

由图6可以看出：在均匀地应力下(mσ=1.00)，井壁切向应力分布形状为圆形(即均匀分布)，在非均匀地应力下，井壁切向应力分布形状由圆形逐渐向“哑铃”状变化(即井壁切向应力差异增加)，若水平地应力比mσ进一步增大，井壁切向应力分布的“哑铃”状更加明显，这是导致井眼失稳的主要原因之一；地应力和弹性模量各向异性系数nE对井壁切向应力均有较大影响，但地应力的影响更为显著；水平地应力差异越大(mσ越小)，井壁切向应力越大，均质地层(nE=1.00)中mσ=0.25与均匀地应力下的井壁切向应力差异为36.13 MPa，横观各向同性地层(nE=0.25)中mσ=0.25与均匀地应力下的井壁切向应力差异为42.88 MPa，可见由于地应力差异造成的井壁切向应力差异达36.13 MPa，而由于地层弹性模量各向异性造成的井壁切向应力差异仅为6.75 MPa，地应力差异的影响比地层各向的影响更为显著。

3.4井筒内钻井液密度对井壁应力的影响

钻开地层形成井眼后，钻井液液柱压力取代了所钻岩层提供的支撑，破坏了地层原有的应力平衡，引起井眼周围岩石的应力重新分布。如果重新分布的应力超过岩石所能承受的最大载荷，将会导致井眼失稳。为此，分析了井筒内钻井液密度(即井筒内压力)对井壁应力的影响，分析结果如图7所示。

由图7可见：无论是均质各向同性地层，还是横观各向同性地层，井筒内钻井液密度对井壁切向应力的分布均有一定的影响，钻井液密度增加，将导致井壁切向应力降低；同时，随着井内钻井液密度的增加，径向应力也显著增加(井壁处径向应力等于井内钻井液液柱压力)；在切向应力降低、径向应力增加的综合作用下，井周分布的应力差异降低，这对维持井周地层稳定(防止剪切破坏)具有重要作用，因此，增加钻井液密度有利于维持井眼稳定性。

4　应用实例

以四川南部长宁—威远页岩气示范区的一口评价井(W201井)为例进行分析，该井1 530 m井段为龙马溪组页岩地层，该地层中层理、页理发育，产状约为60°∠5°，井斜角为3.3°、井斜方位为313.1°，说明井眼与层理相交关系近似垂直关系。因此，采用横观各向同性BEM方法进行计算和分析较合理，基础参数如表1所示，其中，弹性模量各向异性系数nE=0.82，泊松比各向异性系数nυ=0.85，计算得到的结果分别如图8和图9所示。

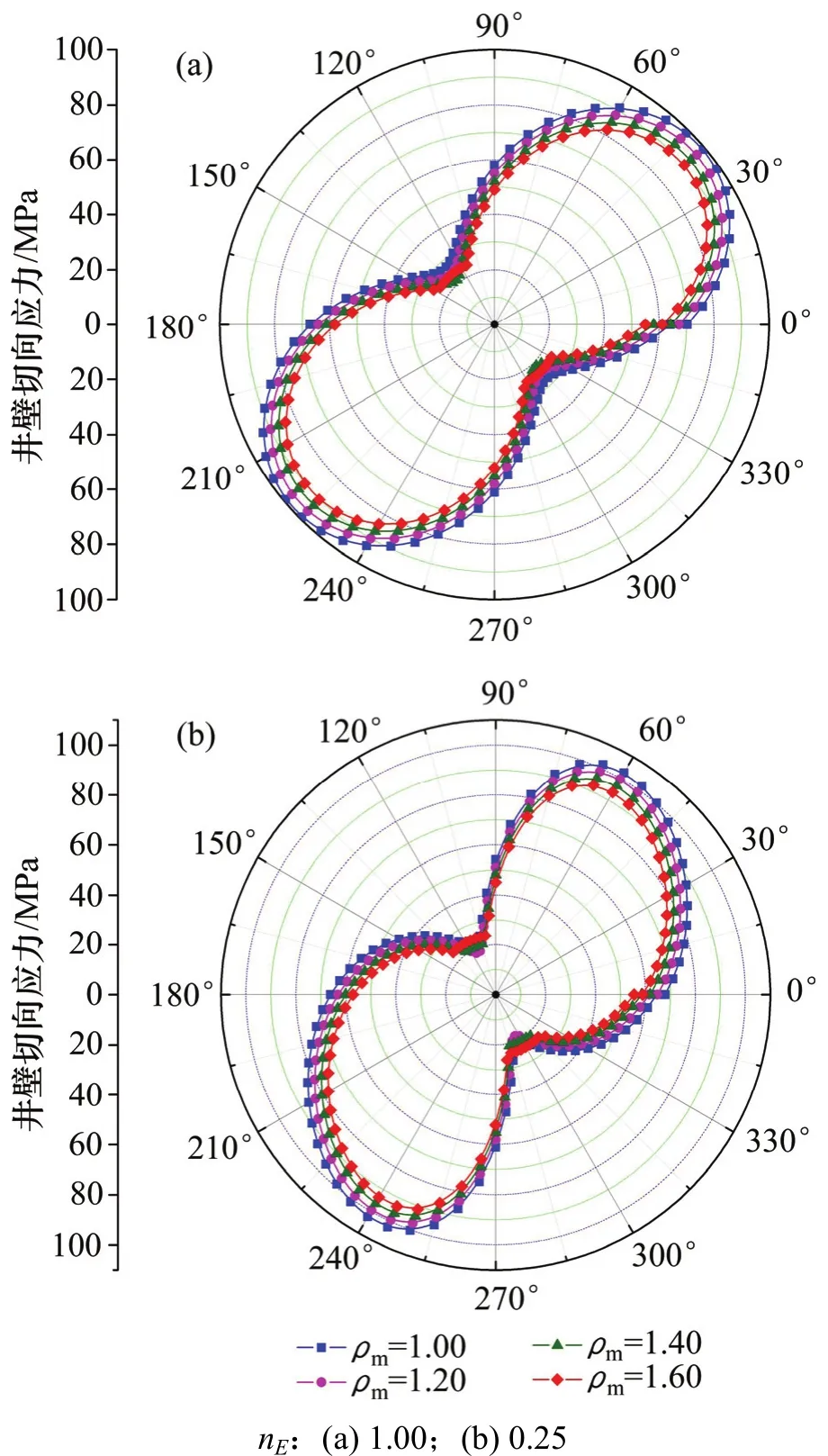
图7　钻井液密度对井壁切向应力分布的影响Fig. 7 Influence of drilling fluid density on tangential stress distribution at borehole wall

由图8和图9可以看出：

1) 若以各向同性介质分析W201井龙马溪组页岩地层井眼稳定问题，采用密度为1.33 g/cm3的钻井液，能够维持井眼稳定。井周地层强度系数大于1.03，强度系数最低的位置在最小水平地应力方向上，即沿图1所示路径a→b之间井周角48°位置，分析结果与前述解析解分析结果一致，进一步验证了方法的准确性和正确性。

2) 若以横观各向同性介质分析W201井龙马溪组页岩地层井眼稳定问题，采用密度为1.33 g/cm3的钻井液，不能够维持井眼稳定，如图8(b)和图8(c)所示的强度系数分布情况。井周地层强度系数最低为0.83，根据强度系数定义，强度系数越低，井眼越不稳定，强度系数最低的位置仍然在最小水平地应力方向上，即路径a→b之间井周角48°的位置。为此，通过提取计算结果，提取出强度系数小于1.0的区域，并绘制成井眼不稳定区域图(见图9)。由图9可以看出：井眼不稳定区域不止发生在井壁上，而是发生在进入地层一定深度处，不安全区域进入地层的深度约为1.09倍井眼半径处，即井眼扩径失稳后将形成9.0%的扩径率，而不稳定区域的井周夹角约为115°。

3) W201井1 530 m井段在实钻过程中，采用密度为1.28 g/cm3的聚磺体系钻井液，完钻电测井径表明该井段井眼扩径率为10%左右。采用各向同性介质计算结果表明，1.28 g/cm3的聚磺体系钻井液能够维持井眼稳定；而采用横观各向同性介质计算结果表明，1.28 g/cm3的聚磺体系钻井液钻进将发生约10%的井眼扩径率。说明本文采用的BEM能够满足井眼稳定问题分析的需求，进一步检验了BEM方法的精度。

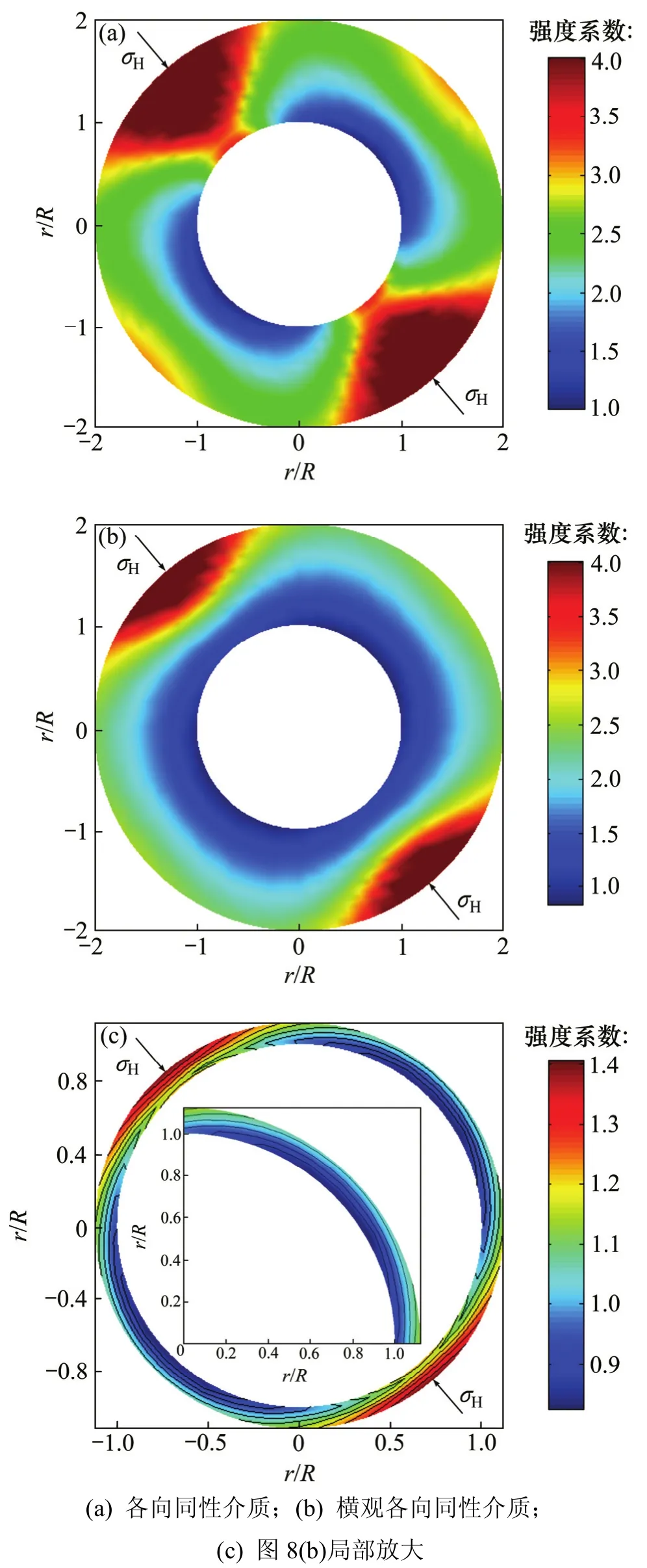
图8　井周地层强度系数分布图Fig. 8 Strength factor distribution around borehole

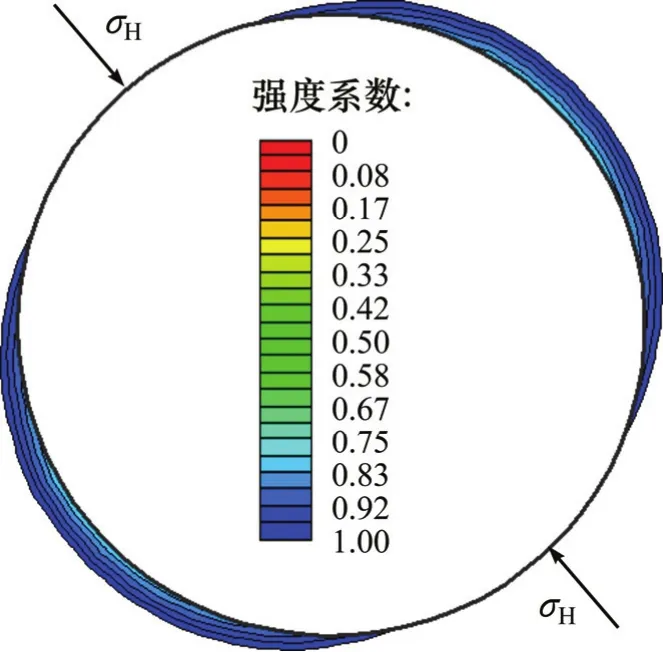
图9　横观各向同性页岩井眼不稳定区域Fig. 9 Instability area around borehole in transverse isotropic shale formation

5　结论

1) 基于各向异性连续介质力学和边界元理论，建立了横观各向同性页岩地层的井眼稳定问题基本微分方程，给出了基本方程的边界积分方程及其离散形式解以及井周应力和位移的边界元离散形式解，结合Mohr−Coulomb准则判别井眼稳定性，形成了基于BEM求解页岩井眼稳定问题的基本方法。

2) 建立了页岩地层井眼稳定问题的BEM求解模型，并以各向同性均质地层为例检验模型，BEM求解结果与解析解吻合较好，二者的相对误差小于2.49%，验证了BEM的正确性与准确性。

3) 在横观各向同性页岩地层中，弹性模量各向异性系数nE、水平地应力比m和井筒内钻井液密度等对井壁应力分布产生显著的影响，而泊松比各向异性系数nυ几乎没有影响。

4) W201井1530井段实例分析表明，采用横观各向同性页岩地层计算结果显示井眼失稳扩径率约9.0%，以各向同性均质地层计算结果显示该井段井眼稳定性较好，而实钻电测资料显示该段井眼扩径率为10.0%左右，说明采用BEM方法并考虑页岩地层的各向异性能够更加准确的判断井眼稳定情况，也进一步验证了本文方法的精度。

[1] 郭彤楼, 张汉荣. 四川盆地焦石坝页岩气田形成与富集高产模式[J]. 石油勘探与开发, 2014, 41(1): 28−36. GUO Tonglou, ZHANG Hanrong. Formation and enrichment mode of Jiaoshiba shale gas field, Sichuan Basin[J]. Petroleum Exploration and Development, 2014, 41(1): 28−36.

[2] 马天寿, 陈平. 基于CT扫描技术研究页岩水化细观损伤特性[J]. 石油勘探与开发, 2014, 41(2): 227−233. MA Tianshou, CHEN Ping. Studies of meso-damage characteristics of shale hydration based on CT scanning technology[J]. Petroleum Exploration and Development, 2014, 41(2): 227−233.

[3] 王红岩, 刘玉章, 董大忠, 等. 中国南方海相页岩气高效开发的科学问题[J]. 石油勘探与开发, 2013, 40(5): 574−579. WANG Hongyan, LIU Yuzhang, DONG Dazhong, et al. Scientific issues on effective development of marine shale gas in southern China[J]. Petroleum Exploration and Development, 2013, 40(5): 574−579.

[4] 陈勉, 金衍, 张广清. 石油工程岩石力学[M]. 北京：科学出版社, 2008: 102−166. CHEN Mian, JIN Yan, ZHANG Guangqing. Rock mechanics on petroleum engineering[M]. Beijing: Science Press, 2008: 102−166.

[5] WESTERGARD H M. Plastic state of stress around a deep well[J]. Journal of Boston Society Civil Engineers, 1940, 27: 387−391.

[6] ROSHAN H, RAHMAN S S. Effects of ion advection and thermal convection on pore pressure changes in high permeable chemically active shale formations[J]. Petroleum Science and Technology, 2013, 31(7): 727−737.

[7] 盛金昌, 刘继山, 许孝臣, 等. 页岩钻孔过程中的流固热化学耦合模型[J]. 工程力学, 2009, 26(12): 240−245. SHENG Jinchang, LIU Jishan, XU Xiaochen, et al. A coupled porochemothermoelastic model for a borehole in shales[J]. Engineering Mechanics, 2009, 26(12): 240−245.

[8] 王倩, 周英操, 王刚, 等. 泥页岩井壁稳定流固化耦合模型[J].石油勘探与开发, 2012, 39(4): 475−480. WANG Qian, ZHOU Yingcao, WANG Gang, et al. A fluid-solid-chemistry coupling model for shale wellbore stability[J]. Petroleum Exploration and Development, 2012, 39(4): 475−480.

[9] 王倩, 周英操, 唐玉林, 等.泥页岩井壁稳定影响因素分析[J].岩石力学与工程学报, 2012, 31(1): 171−179. WANG Qian, ZHOU Yingcao, TANG Yulin, et al. Analysis of effect factor in shale wellbore stability[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(1): 171−179.

[10] 贾善坡, 邹臣颂, 王越之, 等. 基于热−流−固耦合模型的石油钻井施工过程数值分析[J]. 岩土力学, 2012, 33(S2): 321−328. JIA Shanpo, ZOU Chensong, WANG Yuezhi, et al. Numerical analysis of construction process of petroleum drilling based on thermal−hydro−mechanical coupling[J]. Rock and Soil Mechanics, 2012, 33(S2): 321−328.

[11] 李军, 陈勉, 金衍, 等. 大位移井井壁稳定三维弹塑性有限元分析[J]. 岩石力学与工程学报, 2004, 23(14): 2385−2389. LI Jun, CHEN Mian, JIN Yan, et al. Three-dimensional elastoplastic FEM analysis on borehole stability[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(14): 2385−2389.

[12] ROSHAN H, RAHMAN S S. A fully coupled chemo-poroelastic analysis of pore pressure and stress distribution around a wellbore in water active rocks[J]. Rock Mechanics and Rock Engineering, 2011, 44(2): 199−210.

[13] 李嗣贵, 邓金根, 李明志. 节理破碎地层井壁稳定的离散元分析[J]. 岩石力学与工程学报, 2002, 21(S1): 2139−2143. LI Sigui, DENG Jingen, LI Mingzhi. Discrete element analysis on wellbore stability in jointed broken formation[J]. Chinese Journal of Rock Mechanics and Engineering, 2002, 21(S1): 2139−2143.

[14] 屈平, 申瑞臣, 付利, 等. 三维离散元在煤层水平井井壁稳定中的应用[J]. 石油学报, 2011, 32(1): 153−157. QU Ping, SHEN Ruichen, FU Li, et al. Application of the 3D discrete element method in the wellbore stability of coal-bed horizontal wells[J]. Acta Petrolei Sinica, 2011, 32(1): 153−157.

[15] 尹虎, 李黔, 郭亮, 等. 离散单元法评价煤层井壁稳定性[J].天然气工业, 2012, 32(11): 59−63. YIN Hu, LI Qian, GUO Liang, et al. Evaluation of wellbore stability in coal seams by use of the universal discrete element code (UDEC) method[J]. Natural Gas Industry, 2012, 32(11): 59−63.

[16] 邓金根, 郭东旭, 周建良, 等. 泥页岩井壁应力的力学−化学耦合计算模式及数值求解方法[J]. 岩石力学与工程学报, 2003, 22(S1): 2250−2253. DENG Jingen, GUO Dongxu, ZHOU Jianliang, et al. Mechanics−chemistry coupling calculation model of borehole stress in shale formation and its numerical solving method[J]. Chinese Journal of Rock Mechanics and Engineering, 2003, 22(S1): 2250−2253.

[17] 程远方, 张锋, 王京印, 等. 泥页岩井壁坍塌周期分析[J]. 中国石油大学学报(自然科学版), 2007, 31(1): 63−66. CHENG Yuanfang, ZHANG Feng, WANG Jingyin, et al. Analysis of borehole collapse cycling time for shale[J]. Journal of China University of Petroleum (Science & Technology Edition), 2007, 31(1): 63−66.

[18] 邓金根, 刘书杰, 石得勤, 等. 软泥岩井眼弹塑性变形的拉格朗日元法计算[J]. 地质力学学报, 1999, 5(1): 33−37. DENG Jingen, LIU Shujie, SHI Deqin, et al. Calculation of elastoplastic deformation of wellbore in soft mudstone using lagrangian method[J]. Journal of Geomechanics, 1999, 5(1): 33−37.

[19] 邹灵战, 邓金根, 徐显广, 等. 山前高陡构造节理围岩的井壁失稳机制研究[J]. 岩石力学与工程学报, 2008, 27(S1): 2733−2733. ZOU Lingzhan, DENG Jingen, XU Xianguang, et al. Study on wellbore collapse mechanism in jointed rock masses of high-dip-structures before mountains[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(S1): 2733−2733.

[20] WANG H, SOLIMAN M Y, SHAN Z, et al. Understanding the effects of leakoff tests on wellbore strength[J]. SPE Drilling & Completion, 2011, 26(4): 531−539.

[21] BASSEY A, DOSUNMU A, IORKAM A, et al. A new (3D MUDSYSTTM Model) approach to wellbore strengthening while drilling in depleted sands: a critical application of LCM and stress caging model[C]// Nigeria Annual International Conference and Exhibition. Lagos, Nigeria: SPE, 2012: 1−18.

[22] 申光宪. 边界元法[M]. 北京: 机械工业出版社, 1998: 138−224. SHEN Guangxian. Boundary element method[M]. Beijing: China Machine Press, 1998: 138−224.

[23] 张志增, 李仲奎. 横观各向同性岩体中圆形巷道反分析的惟一性[J]. 岩土力学, 2011, 32(7): 2066−2072. ZHANG Zhizeng, LI Zhongkui. Uniqueness of displacement back analysis of a circular tunnel in transversely isotropic rock mass[J]. Rock and Soil Mechanics, 2011, 32(7): 2066−2072.

[24] CHENEVERT M E, GATLIN C. Mechanical anisotropies of laminated sedimentary rocks[J]. SPE Journal, 1965, 5(1): 67−77.

[25] 马天寿, 陈平. 边界元法在深部地层井眼稳定中的应用[J].科技导报, 2015, 33(7): 49−54. MA Tianshou, CHEN Ping. Application of boundary element method to borehole stability problem in deep formation[J]. Science & Technology Review, 2015, 33(7): 49−54.

(编辑 刘锦伟)

Boundary element method and its application to borehole collapse problems in shale formations

MA Tianshou, CHEN Ping
(State Key Laboratory of Oil & Gas Reservoir Geology and Exploitation, Southwest Petroleum University, Chengdu 610500, China)

Based on the anisotropic continuum mechanics and the boundary element theory, the basic differential equations of the borehole collapse problem in transverse isotropic shale formation were established. The boundary integral equation of the basic equations and its discrete solution were deduced, and the discrete solutions of boundary element for stress and displacement were also deduced. The Mohr−Coulomb criterion was used for determining the stability of wellbore, and a basic method for solving borehole collapse by using the boundary element method (BEM) was formed the above processes. The physical model of borehole stability was established for shale formations, the isotropic model was used to verify the correctness of BEM, and the stress distribution around borehole and application example were analyzed by BEM. The results show that the BEM’s solutions are in good agreement with analytical solutions and their relative error is less than 2.49%. The anisotropy of elastic modulus, the differences of horizontal in-situ stress and the density of drilling fluid have significant influence on the stress distribution (the influence of the in-situ stress is the largest), and the influence of the anisotropy of poisson’s ratio is low. The analysis results of 1 530 m section in W201 well are in good agreement with the electric log data, the hole enlargement rate is about 9.0% by BEM, and the hole enlargement rate is about 10.0% by the electric logging data.

shale; borehole stability; transverse isotropy; boundary element method (BEM); numerical method

TE21

A

1672−7207(2016)03−0839−11

10.11817/j.issn.1672-7207.2016.03.017

2015−03−12；

2015−05−20

国家重点基础研究发展计划(973计划)项目(2013CB228003)；四川省国际科技合作与交流项目(2016HH0001) (Project (2013CB228003) supported by the National Basic Research Program (973 Program) of China; Project(2016HH0001) supported by the Scientific Research Foundation of International Cooperation and Exchanges of Sichuan Province)

马天寿，博士，讲师，从事油气井工程方面的教学与科研；E-mail: matianshou@126.com