Effects of liquid compressibility on bubble-bubble interactions between oscillating bubbles*

Yu-ning ZHANG （张宇宁）， Qi MIN （闵琪）， Yu-ning ZHANG （张宇宁）， Xiao-ze DU （杜小泽）

1. State Key Laboratory of Hydroscience and Engineering， Tsinghua University， Beijing 100084， China

2. Beijing Key Laboratory of Emission Surveillance and Control for Thermal Power Generation， School of Energy， Power and Mechanical Engineering， North China Electric Power University， Beijing 102206， China

3. Key Laboratory of Condition Monitoring and Control for Power Plant Equipment （Ministry of Education），North China Electric Power University， Beijing 102206， China， E-mail: y.zhang@ncepu.edu.cn

4. Institute of Nuclear and New Energy Technology， Tsinghua University， Beijing 100084， China

5. College of Mechanical and Transportation Engineering， China University of Petroleum， Beijing 102249， China

Effects of liquid compressibility on bubble-bubble interactions between oscillating bubbles*

Yu-ning ZHANG （张宇宁）1，2，3， Qi MIN （闵琪）4， Yu-ning ZHANG （张宇宁）5， Xiao-ze DU （杜小泽）3

1. State Key Laboratory of Hydroscience and Engineering， Tsinghua University， Beijing 100084， China

2. Beijing Key Laboratory of Emission Surveillance and Control for Thermal Power Generation， School of Energy， Power and Mechanical Engineering， North China Electric Power University， Beijing 102206， China

3. Key Laboratory of Condition Monitoring and Control for Power Plant Equipment （Ministry of Education），North China Electric Power University， Beijing 102206， China， E-mail: y.zhang@ncepu.edu.cn

4. Institute of Nuclear and New Energy Technology， Tsinghua University， Beijing 100084， China

5. College of Mechanical and Transportation Engineering， China University of Petroleum， Beijing 102249， China

The mutual interaction between cavitation bubbles plays an important role in the physical processes of cavitation. In this paper， a complete model is developed for modelling the mutual interaction between cavitation bubbles with the effects of liquid compressibility fully included. It is found that the liquid compressibility is an important parameter in the determination of the direction of the force （the attraction or repulsion force）， as well as the magnitude of the force. The influences of the liquid compressibility on the mutual interaction force can be categorized into three terms: the first is a new term added on the mutual interaction force in incompressible liquids and this term will vanish if the sizes of two bubbles are equal， the second is the radiation damping term， the third one can be considered as a correction of the mutual interaction force in incompressible liquids with a coefficient and this correction will be prominent for small bubbles and a high ambient pressure.

cavitation， Bjerknes force， liquid compressibility， interacting bubbles， bubble cloud

Introduction

The mutual interaction force between cavitation bubbles could affect many important physical processes of cavitation［1-7］， and is an important issue in the cavitation research. For example， the local void fraction in the bubble cloud could be significantly altered by the repulsive or attractive interaction forces between cavitation bubbles， leading to a non-uniform distribution of bubbles in the bubble cloud. Furthermore， the mutual interaction force between cavitation bubbles also plays an important role in the paramount mechanism related with bubbly flows e.g.， the wave propagation［5］， the mass transfer［6］and the jet flow（e.g.， in the hydraulic machinery［7］）. The existence of the mutual interaction force could lead to many interesting phenomena， e.g.， the “bubble grapes”［8］， the“acoustic streamers”［9］and the “cone-like structure”［10］. Hence， a good understanding of the mutual interaction force is essential for an accurate modelling of cavitation and associated physical effects.

In the literature， the mutual interaction force between cavitation bubbles was intensively investigated in last several decades［1-7，11-15］. The directions of the mutual interaction force between cavitation bubbles could be both attractive or repulsive， depending on several paramount parameters （e.g.， the bubble radii and the external excitation）［9］. When the pressure amplitude of the external wave is significant， the induced nonlinear effects （e.g.， harmonics） could also affect both the sign （attraction or repulsion） and the magnitude of the secondary Bjerknes force［14］. A brief review of this topic can be found in Section 11.1 of Lauterborn and Kurz［16］. In a real bubble cloud， a cluster of bubbles （consisting thousands of small bubbles）can be seen. In a rigorous modelling of the bubble cloud dynamics， the interaction forces between those bubbles should be incorporated into the model especially when the void fraction of the bubble cloud is high. Numerous models of bubble cloud dynamics（e.g.， N-bubble model［16，17］） were proposed based on the mutual interaction force. Some bubble cloud models［18，19］considered the mutual interaction forces between bubbles through adding an extra term（summing the radiation pressure generated by all other bubbles at the position of the present bubble） in the bubble equation.

Based on the literature survey， the sign of the mutual interaction force could possibly change with various physical mechanisms （e.g.， the second harmonic， the radiation coupling between bubbles， and the strong acoustic field）. In the present paper， the effects of liquid compressibility are incorporated into the modelling of the mutual interaction force and it is found that the liquid compressibility could also affect the sign of the mutual interaction force and influence the magnitude of the mutual interaction force in certain cases.

1. Basic equations and solutions

In this section， basic equations for the mutual interaction force （specifically termed as “the secondary Bjerknes force” in the following discussions） are shown together with the solutions. Here， a pair of bubbles （numbered as “bubble 1” and “bubble 2”，respectively， for convenience） under the irradiation of the acoustic wave is considered. The radiation pressure generated by the oscillations of bubble 2 at the center of bubble 1 （denoted as1radp） or vice versa can be expressed as

Here，1radp is the radiation pressure generated by the oscillations of bubble 2 at the center of bubble 1， prad2is the radiation pressure generated by the oscillations of bubble 1 at the center of bubble 2，lρ is the density of the liquid， L is the separation distance between the centers of two bubbles， t is the time， R1and R2are the instantaneous bubble radii of bubble 1 and bubble 2， respectively， overdot denotes the time derivative.

With the interaction forces between bubbles （e.g.，the radiation pressure generated by other bubbles）， the equation of bubble motion can be modified as （Eq.（7） of Mettin et al.［15］）

where

Here，lc is the undisturbed speed of sound in the liquid，0P is the ambient pressure， σ is the surface tension coefficient，10R and20R are the equilibrium bubble radio of bubble 1 and bubble 2， respectively，κ is the polytropic exponent，lμ is the viscosity of the liquid，thμ is the effective thermal viscosity， ε is the non-dimensional amplitude of the driving sound wave， ω is the angular frequency of the driving sound wave. The details about predictions of thermal effects （e.g.， values of κ andthμ in Eqs.（5） and （6））can be found in Ref.［20］ and our previous work［21，22］. In the present paper， κ andthμ are predicted using the following formulas［20，22］，

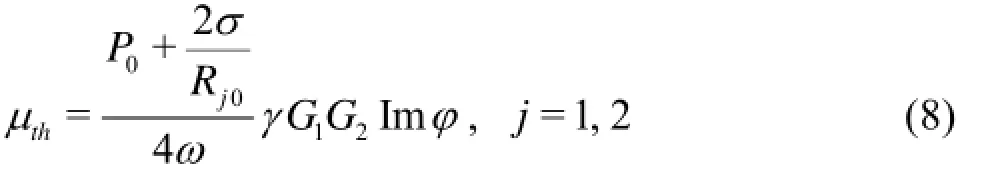
with

Here， γ is the specific heat ratio， gM is the molecular weight of the gas in the bubble， ，gvD is the thermal diffusivity of the gas defined under the constant volume condition，gR is the universal gas constant， T∞is the ambient temperature.

The solutions of Eqs.（3） and （4） are

Substituting Eqs.（18） and （19） into Eqs.（3） and（4）， one obtains

where

Here， =1，2j，0jω is the natural frequency of the bubble j，jβ，vjβ，thjβ andacjβ are the total， viscous， thermal and acoustic damping constants of the bubble j， respectively. In the present paper， only linear oscillations of bubbles are considered. Hence，up to the first order， ε，1x and2x are

Substituting Eqs.（28） and （29） into Eqs.（20） and（21）， we obtain

Solving Eqs.（30） and （31）， we obtain

with

Because the secondary Bjerknes force on bubble 1 is equal to that on bubble 2， we only need to determine one of them （e.g.， the force on bubble 1）. The secondary Bjerknes force is

Here，BF denotes the secondary Bjerknes force，1v is the instantaneous volume of the bubble 1，2p∇ is the pressure gradient generated by bubble 2 at the center of bubble 1，denotes the time average，12e is the unit vector pointing from bubble 1 to bubble 2. Here，the complex analysis will be employed and we define v1=Im（V1） and ∇p2=Im（∇P2） following the framework of Ref.［14］. In the linear regimes， Eqs.（36） and（37） can be expressed as

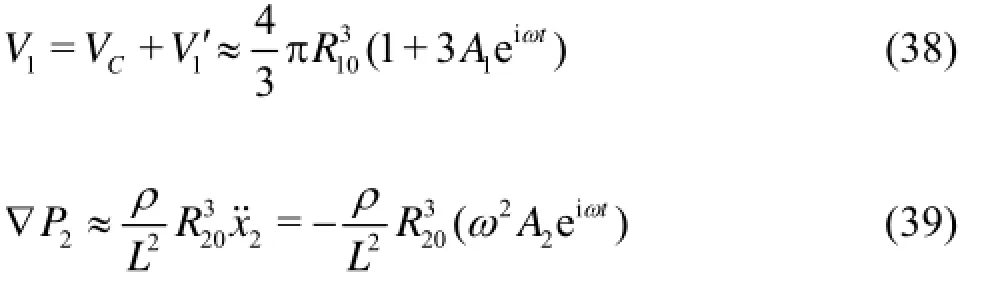
In Eq.（38）， the first term is a constant and. Hence this term will not contribute to the secondary Bjerknes force. If we choose the time period for the time averaging in Eq.（35） conveniently（e.g.， leading to e2iωt=0， one can obtain the secondary Bjerknes force such as

Here， the bar over the symbol denotes the complex conjugate. Substituting Eqs.（38） and （39） into Eq.（40），we obtain

2. Effects of liquid compressibility

In this section， the expression of the secondary Bjerknes force （Eq.（41） in Section 1） is simplified for convenient discussions of the effects of the liquid compressibility. For the conciseness of demonstration，we will split the terms contributed by the effects of the liquid compressibility in the expressions of the secondary Bjerknes force. There are totally three terms involving the effects of compressibilityjβ，jM， Nj（j=1，2）， in Eqs.（23）， （26） and （27）， respectively. Here， only terms up to the order ofwill be considered. Based on Eqs.（26） and （27）， we obtain，

20 than2ω， hence for convenience， we add term1（/Ninto the bracket of Eq.（32） and terminto the bracket of Eq.（33）. Then Eqs.（32） and （33） becomes

Substituting Eq.（46） into Eq.（41）， we obtain the final simplified equation of the secondary Bjerknes force

with

The liquid compressibility contributes to the secondary Bjerknes force through three ways. The first way is through the acoustic damping terms in1β and2β inBF～ （Eq.（49））. Its details can be made clear in Eq.（23） in Section 1. In these terms， in contrast with the previous work （e.g.， Ref.［14］）， the acoustic radiation dampingacjβ and the thermal dampingthjβ are further considered in the theory， leading to the dissipation of energy through the scattered wave and the heat transfer， respectively. As other damping terms （e.g.，viscous and thermal damping mechanisms）， the term related with the liquid compressibility （containing βacj） takes a positive value and will influence the position for the change of the sign of the secondary Bjerknes force. If we neglect the acoustic and thermal damping mechanisms （βac=βth=0） in β1and β2，F～Bin Eq.（34） will be reduced to the form in the previous work by Doinikov［14］，

with

If we further neglect the viscous damping terms（βv1=βv2=0）， Eq.（52） reduces to

with

MHD方程组是由Navier-Stokes方程和Maxwell方程耦合形成的，在工业和工程领域都有着重要的应用，比如核反应的冷却、金属的冶炼过程以及铝合金的制造。所以许多学者对MHD方程组提出自己的算法，Gunzburger[1]等人提出一种有限元方法求解不可压缩的MHD方程组。对于非线性问题，Layton[2]和他的合作者提出两水平方法提高计算效率。在这个算法的启发下，吴技莲和黄明展[3]提出两步算法求解MHD方程组。另一类高效方法是并行算法，尚月强[4-6]基于区域分解技术提出了并行有限元方法。本文研究的MHD模型如下：

If we further ignore the interaction term （the last term in Eqs.（3） and （4）） between two bubbles through radiation pressure， then the bubble will only be excited by the incident sound wave. In this case， one can easily obtain the following expression by setting ξ1=ξ2=0 in Eq.（54），

This is the well-known formula obtained by Bjerknes.

The second contribution of the liquid compressibility to the secondary Bjerknes force is through the term K in Eq.（47）. As K=1-τ＜1， this term will reduce the secondary Bjerknes force. Based on Eqs.（23）and （48）， τ is directly proportional to lμ and thμ and is inversely proportional to the speed of sound （cl） and the bubble radii （10R and20R）.

The third contribution of the liquid compressibility to the secondary Bjerknes force is through the term＇. If two bubbles are of an equal size10（=R R20）， this term will vanish （i.e.，＇=0）. For bubbles of unequal sizes，＇ generally takes a positive value.

3. Results and discussions

In this section， we demonstrate the influences of the liquid compressibility on the secondary Bjerknes force through demonstrating examples. For convenience， air bubbles in water are considered. If not specified， the following physical properties are adopted in the present paper P0=1.013×105Pa ， ρl= 1000kg/m3，=1486m/s ， μ=0.001Pa·s ， σ=l0.0728N/m. In the calculations of κ and μth， the following constants are employed: Dg，v=2.90× 10-5m2/s ， γ=1.40，=28.97g/mol， R= g 8.314J/mol·K-1，=293.15K . Firstly， we will consider the influence of the term＇ in Eq.（47） on the secondary Bjerknes force. For the convenience of comparison， we will set K=1 in Eq.（47） and define a non-dimensional coefficient ζ such as

Hence， ζ reflects the ratio between the secondary Bjerknes forces with and without the term＇. As shown in Eq.（47），only exists for bubbles of unequal sizes. Here， we assume R10＜R20， hence， according to Eq.（22）， ω02＜ω01. Based on Eq.（50）， in most cases，＇ should be positive and one also can find that the value ofis nearly directly proportional to ωR20/cl. For large values of ωR20/cl， ω≫ω02. In this region， with the increase of R10， the sign of the secondary Bjerknes force will change from negative（repulsion） to positive （attraction） values， because initially ω02＜ω＜ω01and then ω＞ω01＞ω02. Therefore， due to the existence of the positive term＇， the regions with the attractive secondary Bjerknes force will be enlarged.

Fig.1 Comparisons of ζ versus bubble radii R10for different values of ωR20/cl（R20=10-4m）. The dashdotted line refers to ζ=0

Figure 1 shows the comparisons of ζ for different values of ω/c. In Fig.1， we fix=10-4m ，lwith the values of R10varying from 10-7to 10-4. For a small value of ωR20/cl， ζ≈1， which means the correction of the term FB＇ can be ignored （referring to Eq.（57））. With the increase of ωR20/cl， ζ shows fluctuations and the correction of the term FB＇ is important in certain regions. When ωR20/cl=0.667，the corresponding resonance bubble radius （Rr） is 2.1×10-6m. For R10＜Rr， the secondary Bjerknes force takes a negative value， because ω02≪ω≪ω01，while for R10＞Rr， the secondary Bjerknes force takes a positive value， because ω02≪ω01＜ω. For an intermediate value of ωR20/cl（e.g.， 0.667 in Fig.1）， ζ oscillates near the resonance. With the increase of R10below the resonance （R10＜Rr）， ζ will initially decrease because FB＇ is positive and it will counteract some part of the negative value of F～B， then after passing the resonance （R10＞Rr）， ζ will increase because both＇ andare positive. With a further increase of R10， R10will be close to R20. Then ζ approaches to 1 because the correction term＇ is directly proportional to （R20-R10） according to Eq.（50）. In those cases， F～Bis a dominant term and the sign of the secondary Bjerknes force keeps unchanged. If we further increase ωR20/cl（e.g.， 3.333 in Fig.1）， the corresponding resonance bubble radius（Rr） is 5.7×10-7m. Then， both the amplitude and the regions of oscillations of ζ become quite large as shown in Fig.1. In this case， ζ also takes negative values， meaning thatis negative while+＇ is positive.

Fig.2 Comparisons of K for air bubbles. R10=R20（ω= 106s-1）

Now， we will consider the correction term K in Eq. （47）. For convenience， we assume that R10=R20to make the term FB＇ vanish in Eq.（47）. In the literature， most of theoretical and experimental investigations focused on the dynamics of cavitation bubbles inthe liquids under atmospheric conditions. Recently，the acoustic cavitation in high-pressure liquids （e.g.，the liquid carbon dioxide） has attracted much attention of many researchers， e.g.［23］. For ordinary solvents， the sonochemical investigations are often performed under atmospheric conditions due to the difficulties of generation of cavitation at high pressure. However， for the high-pressure liquid carbon dioxide， the threshold of the acoustic cavitation is relatively low as the vapor pressure of the liquid is quite high. Furthermore， as a green solvent and reactant， the liquid carbon dioxide is cheap， nontoxic and apyrous.

Fig.3 Variations of μthversus bubble radii for air bubbles R10=R20. The viscosities of the water， blood and highpressure liquid carbon dioxide are also marked in the figure （ω=106s-1）

Figure 2 shows the predictions of K in three cases: air bubbles in water and blood， cavitation in the high-pressure liquid carbon dioxide. For physical properties of blood， we only modify the liquid viscosity such as μl=0.005Pa·s . For the high-pressure liquid carbon dioxide， the following physical properties are employed in calculations［23，24］: P0=5.2×106Pa ， ρl= 825kg/m3， cl=394m/s ， μl=7×10-5Pa·s ， σ= 2×10-3N/m ， D=2.62×10-7m2/s ， γ=1.28，

4. Conclusion

In the present paper， the influences of the liquid compressibility on the secondary Bjerknes force are demonstrated in three corrections. The first one is a new positive term added on the secondary Bjerknes force in incompressible liquids. This term is directly proportional to the non-dimensional parameter20/Rω cland will disappear if R10=R20. The second one is the radiation damping term， which will influence the position of the sign reversal of the secondary Bjerknes force during the variations of the frequencies of acoustic waves. The third one is a linear correction of the secondary Bjerknes force in incompressible liquids through a coefficient. This correction is prominent for small bubbles and high ambient pressure. The importance of the mutual interactions force is of great interest for many practical applications （e.g.， hydroturbines［25，26］）.

Acknowledgement

This work was supported by the Open Research Fund Program of State Key Laboratory of Hydroscience and Engineering， Tsinghua University （Grant No. sklhse-2015-E-01）.

References

［1］ZHANG Y.， ZHANG Y. and LI S. The secondary Bjerknes force between two gas bubbles under dualfrequency acoustic excitation［J］. Ultrasonics Sonochemistry， 2016， 29（3）: 129-145.

［2］JIAO J.， HE Y. and YASUI K. et al. Influence of acoustic pressure and bubble sizes on the coalescence of two contacting bubbles in an acoustic field［J］. Ultrasonics sonochemistry， 2015， 22（1）: 70-77.

［3］JIAO J.， HE Y. and KENTISH S. E. et al. Experimental and theoretical analysis of secondary Bjerknes forces between two bubbles in a standing wave［J］. Ultrasonics，2015， 58（4）: 35-42.

［4］VANHILLE C.， CAMPOS-POZUELO C. Numerical simulations of the primary Bjerknes force experienced by bubbles in a standing ultrasonic field: Nonlinear vs. linear［J］. Wave Motion， 2014， 51（7）: 1127-1137.

［5］FUSTER D.， CONOIR J. M. and COLONIUS T. Effect of direct bubble-bubble interactions on linear-wave propagation in bubbly liquids［J］. Physical Review E， 2014， 90（6）: 063010.

［6］ABOULHASANZADEH B.， TRYGGVASON G. Effect of bubble interactions on mass transfer in bubbly flow［J］. International Journal of Heat and Mass Transfer， 2014，79: 390-396.

［7］LUO Xian-wu， JI Bin and TSUJIMOTO Yoshinobu. A review of cavitation in hydraulic machinery［J］. Journal of Hydrodynamics， 2016， 28（6）: 335-358.

［8］DOINIKOV A. A.， ZAVTRAK S. T. On the mutual interaction of two gas bubbles in a sound field［J］. Physics of Fluids， 1995， 7（8）: 1923-1930.

［9］PELEKASIS N. A.， GAKI A. and DOINIKOV A. et al. Secondary Bjerknes forces between two bubbles and the phenomenon of acoustic streamers［J］. Journal of Fluid Mechanics， 2004， 500: 313-347.

［10］ MOUSSATOV A.， GRANGER C. and DUBUS B. Conelike bubble formation in ultrasonic cavitation field［J］. Ultrasonics sonochemistry， 2003， 10（4）: 191-195.

［11］ HARKIN A.， KAPER T. J. and NADIM A. Coupled pulsation and translation of two gas bubbles in a liquid［J］. Journal of Fluid Mechanics， 2001， 445: 377-411.

［12］IDA M. A characteristic frequency of two mutually interacting gas bubbles in an acoustic field［J］. Physics Letters A， 2002， 297（3）: 210-217.

［13］ IDA M. Alternative interpretation of the sign reversal of secondary Bjerknes force acting between two pulsating gas bubbles［J］. Physical Review E， 2003， 67（5）: 056617.

［14］ DOINIKOV A. A. Effects of the second harmonic on the secondary Bjerknes force［J］. Physical Review E， 1999，59（3）: 3016.

［15］ METTIN R.， AKHATOV I. and PARLITZ U. et al. Bjerknes forces between small cavitation bubbles in a strong acoustic field［J］. Physical review E， 1997， 56（3）: 2924.

［16］ LAUTERBORN W.， KURZ T. Physics of bubble oscillations［J］. Reports on Progress in Physics， 2010， 73（10）: 106501.

［17］ METTIN R.， LUTHER S. and OHL C. D. et al. Acoustic cavitation structures and simulations by a particle model［J］. Ultrasonics Sonochemistry， 1999， 6（1）: 25-29.

［18］AN Y. Nonlinear bubble dynamics of cavitation［J］. Physical Review E， 2012， 85（1）: 016305.

［19］ IDA M. Bubble-bubble interaction: A potential source of cavitation noise［J］. Physical Review E， 2009， 79（1）: 016307.

［20］ PROSPERETTI A. Thermal effects and damping mechanisms in the forced radial oscillations of gas bubbles in liquids［J］. The Journal of the Acoustical Society of America， 1977， 61（1）: 17-27.

［21］ ZHANG Y.， LI S. C. Notes on radial oscillations of gas bubbles in liquids: Thermal effects［J］. The Journal of the Acoustical Society of America， 2010， 128（5）: EL306-EL309.

［22］ ZHANG Y. Heat transfer across interfaces of oscillating gas bubbles in liquids under acoustic excitation［J］. International Communications in Heat and Mass Transfer，2013， 43（4）: 1-7.

［23］ Van IERSEL M. M.， CORNEL J. and BENES N. E. et al. Inhibition of nonlinear acoustic cavitation dynamics in liquid CO2［J］. The Journal of Chemical Physics， 2007， 126（6）: 064508.

［24］LIDE D. R. Chemistry and physics［M］. Boca Raton， FL，USA: CRC Press， 2012.

［25］ ZHANG Y.， QIAN Z. and JI B. et al. A review of microscopic interactions between cavitation bubbles and particles in silt-laden flow［J］. Renewable and Sustainable Energy Reviews， 2016， 56（4）: 303-318.

［26］ ZHANG Y.， ZHANG Y. and WU Y. A review of rotating stall in reversible pump turbine［J］. Proceedings of the Institution of Mechanical Engineers， Part C： Journal of Mechanical Engineering Science， 2016， 9（4）: 1403-1430.

（March 10， 2015， Revised May 12， 2016）

* Project supported by the National Natural Science Foundation of China （Grant Nos. 51506051， 51606221）.

Biography： Yu-ning ZHANG （1983-）， Male， Ph. D.，

Associate Professor