具有阻感负载的三相双向混合电压型整流器的研究
2016-12-06厍冬瑾王久和翟丹丹
厍冬瑾,王久和,翟丹丹
(北京信息科技大学自动化学院,北京 100192)
具有阻感负载的三相双向混合电压型整流器的研究
厍冬瑾,王久和,翟丹丹
(北京信息科技大学自动化学院,北京 100192)
对一种三相混合电压型PWM整流器进行了研究。根据拓扑结构分别建立了Boost变换器的欧拉-拉格朗日EL(Euler-Lagrange)数学模型和PWM整流器的端口受控耗散哈密顿PCHD(port control hamiltonation with dissipation)模型。PCHD模型进行无源控制器设计不仅能进行阻尼注入,还能进行能量成型,无源控制器设计更为灵活。基于三相混合电压型整流器的无源性,采用一种外环采用PI控制,内环采用无源控制的无源混合控制方案。仿真验证了该无源混合控制器在整流器带阻感负载情况下运行的可行性。
混合整流器;无源控制;功率分配;功率密度
本世纪初国外学者提出了单向混合三相电压型整流器(unidirectional hybrid three phase voltage source rectifier,UHTPVSR)[1]的概念。UHTPVSR由1个三相单管整流器(Z1)和1个二或三电平PWM整流器(Z2)并联组成,二者共同为同一负载供电,其拓扑结构如图1所示。
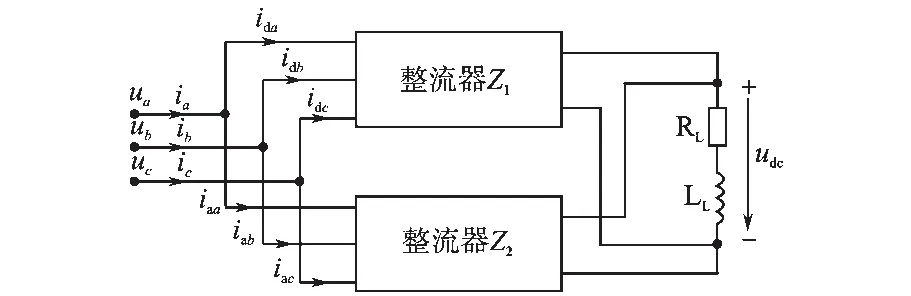
图1 UHTPVSR拓扑结构简图(阻感负载)Fig.1 Sketch topology of UHTPVSR(resistance-inductance load)
整流器Z1借助二极管整流器的可靠性高、效率高的特点,通常设定在低频、大功率运行;整流器Z2即PWM型整流器可设定在高频、小功率运行,减少了系统的体积、重量,从而提高了功率密度,降低了总谐波畸变率(THD)。由于整流单元Z1只处理系统1/3左右的功率,降低了主开关器件的导通电流,所以基于混合整流器拓扑结构的方案,相比基于单个可控整流器的方案,可以获得更高的效率[2],而且有效降低了成本。
为满足工业对整流器的综合性能的要求,三相混合整流器存在一些关键问题亟待解决[3-4]:
1)交流侧输入电流畸变问题。UHTPVSR网侧输入电流ia,ib,ic由整流器Z1的输入电流idi和整流器Z2的输入电流iai合成,在两部分电流叠加时,整流器Z1和Z2的期望电流将会在π/6,5π/6或7π/6,11π/6切换点处形成突变,而整流器Z2无法跟踪突变电流,因而在切换点处形成电流畸变(如图2所示),使UHTPVSR网侧无法形成正弦输入电流,使THD(总谐波失真)偏高。
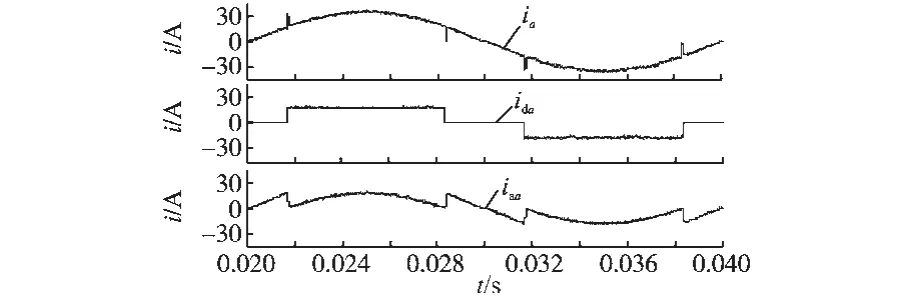
图2 UHTPVSR输入电流Fig.2 Input current of UHTPVSR
2)二极管整流器Z1和PWM型整流器Z2的功率分配问题。在国外文献中,由二极管整流器和两电平单向Y开关整流器组成的UHTPVSR[2]要求二极管整流器功率所占比例Pd∶Po>0.552;二极管整流器与两电平单向△开关电压型PWM整流器组成的UHTPVSR[5-6]要求功率分配比为Pd∶Po>0.43,功率分配比例范围较小,限制了UHTPVSR的性能优势。
3)UHTPVSR的控制问题。文献[1,4-7]采用PI控制器的多环控制结构,文献[8]采用基于PR控制器的多环控制结构。但是以上基于线性系统的控制方法,不能对非线性系统进行有效控制,跟踪突变电流能力差,影响了UHTPVSR的性能。
本文在国内外研究的基础上,针对以上问题,对UHTPVSR的拓扑结构进行改进,并提出了更优化的功率分配方法,并提出一种内环采用无源控制[9-10],外环采用PI控制的无源混合控制方案,使三相混合整流器具有更好动静性能和抗干扰性。
1 混合整流器的拓扑结构和工作原理
1.1 混合整流器的拓扑结构
本文的研究对象为带阻感性负载的能量可双向流动的混合三相电压型整流器(hybrid three phase voltage source rectifier,HTPVSR),拓扑结构如图3所示。
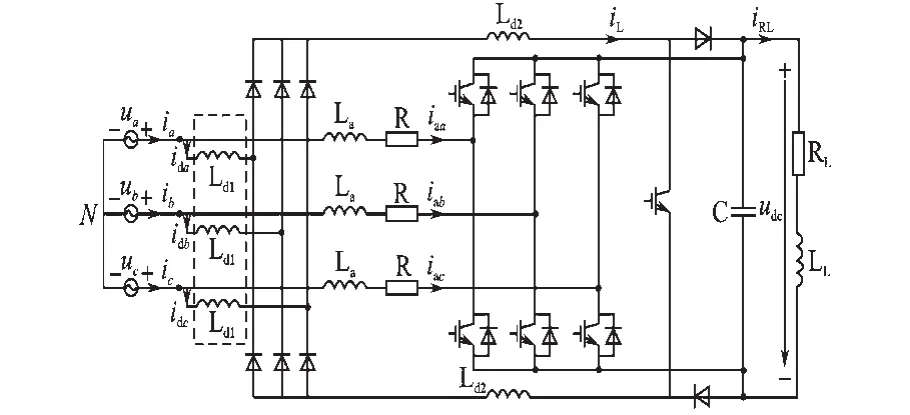
图3 三相混合整流器拓扑结构Fig.3 The topology of HTPVSR
在图3所示的HTPVSR中,整流器Z1是带有Boost升压单元的二极管桥式整流器,工作在连续导通模式(CCM),整流器Z2选择能量双向流通的两电平PWM整流器。
在现行控制方法中,ida波形为矩形波,在换相点处不易跟踪控制,于是在HTPVSR输入电流的切换点处形成电流畸变(如图2所示)。本文在HTPVSR三相交流侧添加小电感Ld1(见图3虚线框),同时对期望电流进行模拟小电感的滤波处理(图4中①~④处),从而使ida和iaa在切换点平滑,改善了控制器的跟踪效果,有效抑制了HTPVSR交流侧各相输入电流畸变。加小电感滤波后的a相输入电流波形如图5所示。
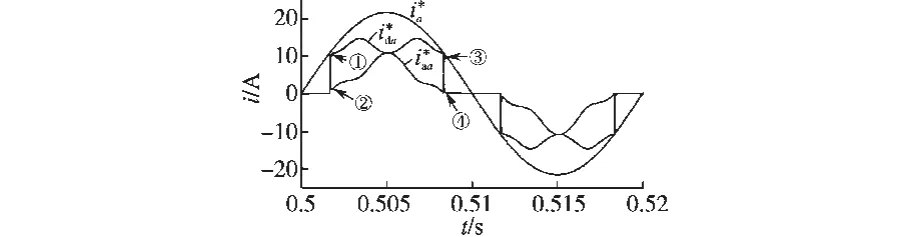
图4 HTPVSR的a相期望电流波形Fig.4 Expected phase a current waveforms of HTPVSR

图5 添加小滤波电感后HTPVSR的a相输入电流Fig.5 The phase a current of HTPVSR after adding small filtering inductance
1.2 混合整流器功率分配原理
UHTPVSR网侧输入电流ia,ib,ic由整流器Z1,Z2的输入电流idi,iai合成,即ii=idi+iai(i=a,b,c)。且为保证UHTPVSR在高功率因数下运行,ia,ib,ic应为与输入三相交流电压同步的正弦波。
由于工频6脉波信号幅值的可控性,可以利用iu的波形系数k来调节电流iu幅值的大小,也就调节了ida有效值的大小,由Pa1=Ua·Ida,Pa2=Ua·Iaa可知,调节k值可以调节两部分有功功率比例。
以a相为例,Boost变换器的期望电流i∗da为
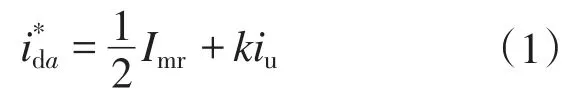
式中:Imr为三相电源的单相输入线电流峰值;k为i*da交流部分iu的波形系数,即功率调节因子。设iuP为iu的幅值,两部分负载承担的有功功率比例分别为
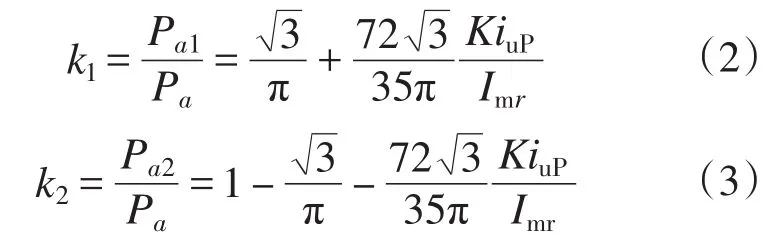
对于Z2为单向整流器的情况,与传统为方波的控制方法相比,功率分配比例的最大值由原来k1∶k2=0.57∶0.43提高到k1∶k2=0.76∶0.24。
2 混合整流器数学模型及控制策略
为建立其数学模型,假设图2的拓扑结构中:1)电源为三相对称正弦电压;2)滤波电感是线性的,且不考虑饱和;3)开关为理想开关,无导通关断延时,无损耗。
2.1 电压外环的设计
考虑到直流侧电压udc的动态性,整流器电压外环采用PI控制器,使udc快速收敛并稳定于期望值。电压外环传递函数为
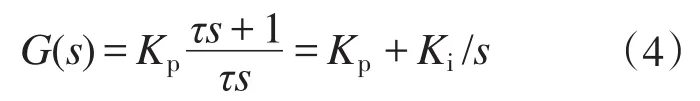
可按照典型Ⅱ型系统分别计算整流器Z1,Z2的Kp,Ki值,然后根据实际仿真情况在计算范围内选取系统的Kp,Ki值。
2.2 Boost型DC-DC变换器的数学模型和无源控制器设计
2.2.1 Boost型DC-DC变换器的数学模型
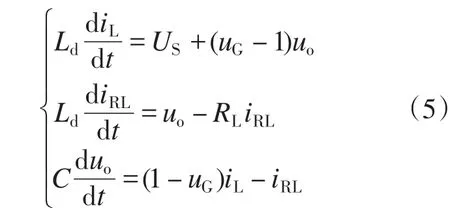
由图2得变换器的动态方程为取电感电流iL、负载电流iRL和电容电压uo作为状态变量,即 x1=[x1x2x3]T=[iLiRLuo]T,由式(5)可得变换器的EL模型:
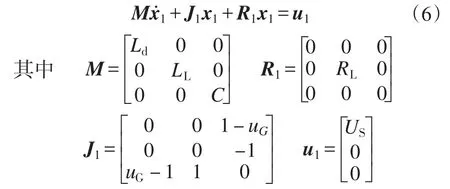
由于J1=-JT1为反对称矩阵且R1为正定矩阵,式(6)具有EL方程的特性。
2.2.2 Boost型DC-DC变换器无源控制器设计
根据EL模型式(6),设xe1=x1-x*1,瞬态期望平衡点 x*1=[x*1x*2x*3]T=[i*Li*RLu*o]T,令变换器误差存储函数为
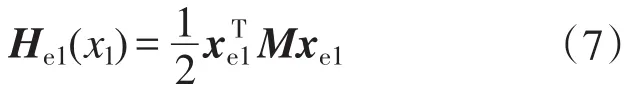
为使误差能量快速变为零,需注入阻尼Ra1,注入阻尼耗散项为Rd1xe1=(R1+Ra1)xe1,正定对角阻尼矩阵Ra1=diag{ra1,ra2,1/ra3}(rai>0)。则式(6)可变为
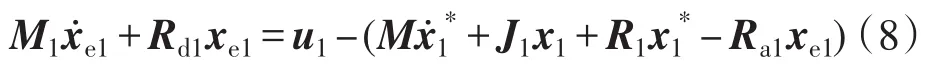

由此可得变换器的开关函数为
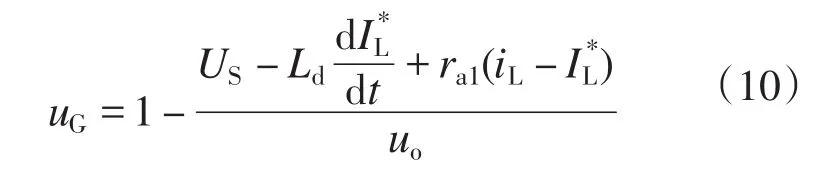
2.3 PWM整流器的数学模型和无源控制器设计
2.3.1 PWM整流器的数学模型
定义Sj(j=a,b,c)为控制开关管的单极性二值逻辑开关函数,Sj=1对应上桥臂导通,下桥臂关断,Sj=0对应下桥臂导通,上桥臂关断。根据图3,三相PWM整流器在dq坐标系下数学模型为

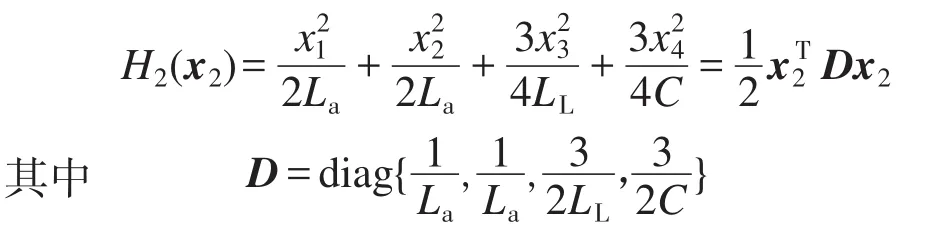
由式(11)得到变换器的PCHD模型
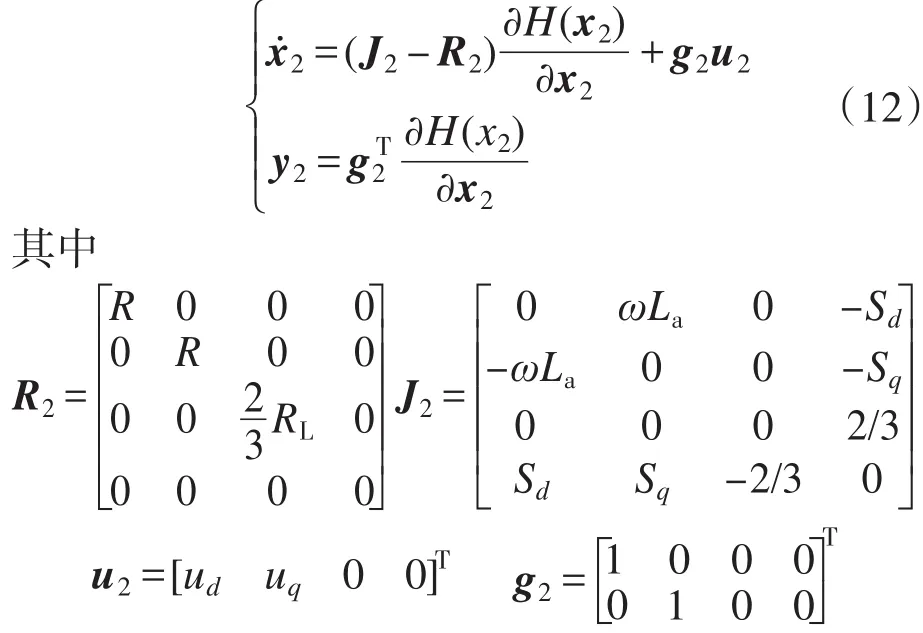
式中:J2=-J2T为反对称矩阵;R2为正定矩阵。
2.3.2 IDA-PBC设计
为使系统收敛于期望的稳定平衡点x*1,另外构造1个闭环哈密顿函数Hd2(x2),且Hd2(x*2)=0。对于任意1个x2≠x*2,有Hd2(x2)>0。
配置互联矩阵 Ja2(x2)和期望阻尼矩阵Ra2(x2),使
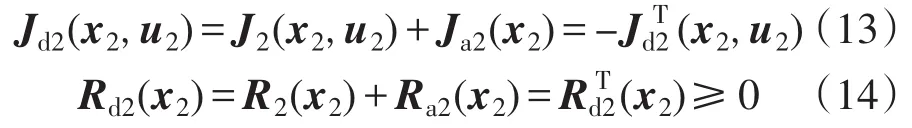
通过反馈控制律u2=a(x2)使系统式(12)成为闭环耗散PCHD系统:

根据式(12)和式(15)求得:
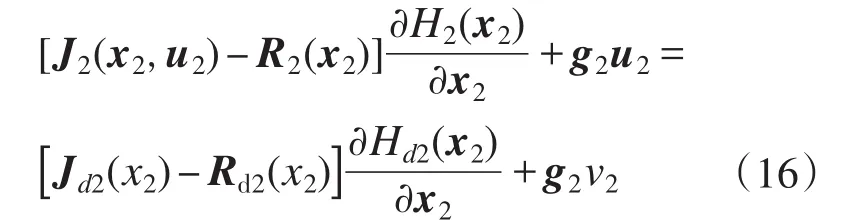
取期望误差能量存储函数:
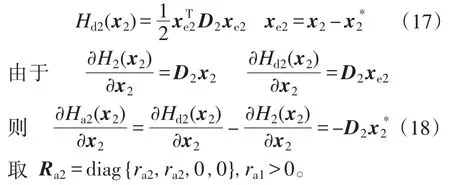
联立式(12)~式(18),取g2u2+Jd2D2xe2=0,可得闭环哈密顿函数对时间的导数为

此时PWM整流器PCHD模型系统的误差能量函数是收敛的,可得PWM整流器的无源控制器:
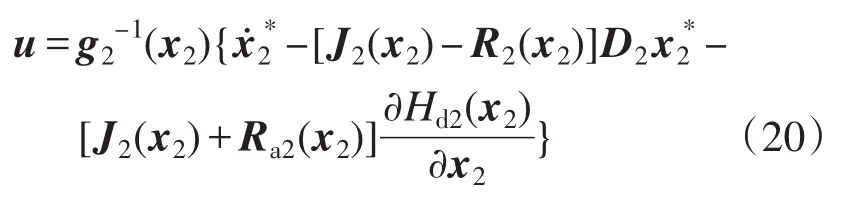
经计算,得到PWM整流器的控制律为
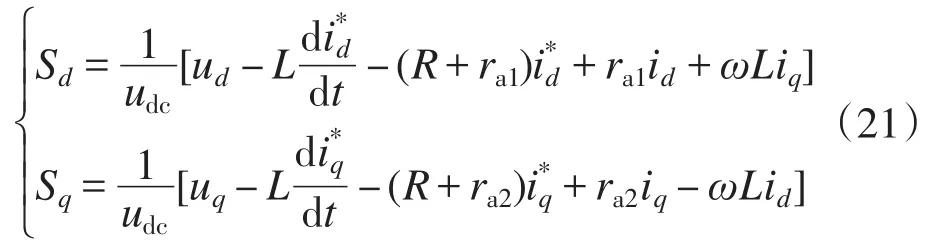
由以上控制策略得出三相混合电压型整流器的控制框图如图6所示。

图6 三相混合电压型整流器的控制结构图Fig.6 Control block diagram of HTPVSR
3 仿真实验研究及结论
用Matlab/Simulink软件对系统进行仿真,电源相电压220 V,f=50 Hz;整流器Z1升压电感Ld2= 7 mH,PWM整流器电感La1=La2=La3=1.95 mH,电容C=1 800 μF;工作频率fZ1=10 kHz,fZ2=20 kHz,输出电压期望值udc*=800 V。无源控制器阻尼注入ra1=250,ra2=2 000。电压外环PI参数选取Kp= 0.001,Ki=4.6。波形系数k=15,由式(2)、式(3)计算得两部分功率因数分配比例k1∶k2≈0.6∶0.4。
额定负载(R=64 Ω,L=50 mH)时的仿真结果如图7~图11所示。

图7 三相混合整流器直流输出电压波形Fig.7 The output DC voltage waveforms of three-phase hybrid rectifier
由图7~图11可以看出,稳态时整流器直流侧输出电压udc在无源混合控制器作用下于0.01 s时达到期望值800 V,而在传统PI控制器作用下在0.04 s达到期望值,传统6开关PWM整流器在0.4 s达到期望值;网侧交流电压、电流稳态平衡;功率因数λ=0.999 6;总谐波失真THD=2.71%,与PI控制3.9%相比进一步降低。仿真实现了系统输入电流的正弦化,稳定的直流电压输出和单位功率因数,并实现了谐波失真THD<5%的目标。
图12为混合整流器带阻感负载时,负载在0.2s由额定值RL=64Ω,LL=50mH突变为RL=32Ω,LL=30 mH,在0.7 s又变回额定值时整流器输出电压波形。由波形可知,系统在阻感负载2次突变时均能快速恢复到额定输出电压,体现了混合整流器在无源混合控制器作用下具有很强的抗干扰性能。
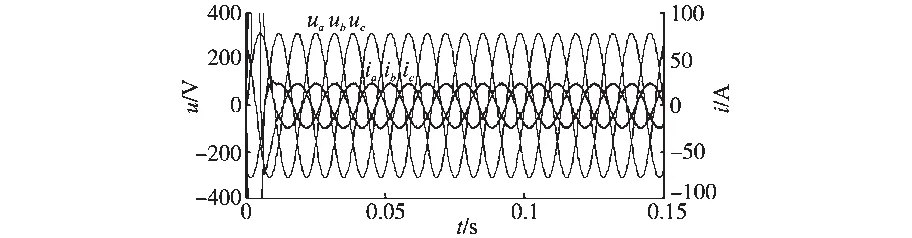
图8 三相混合整流器的三相交流电压、交流电流波形Fig.8 The three-phase AC voltage and current waveforms of three-phase hybrid rectifier
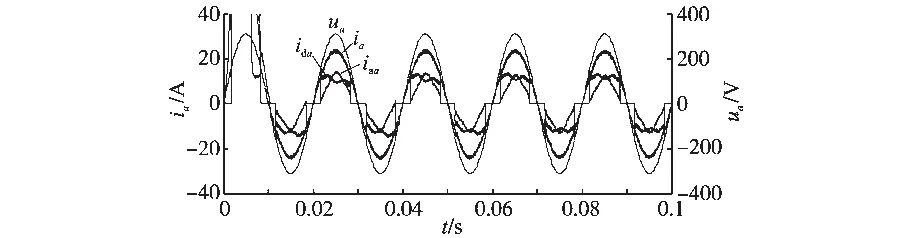
图9 混合三相电压型整流器的a相线电流波形Fig.9 The a phase current waveforms of HTPVSR
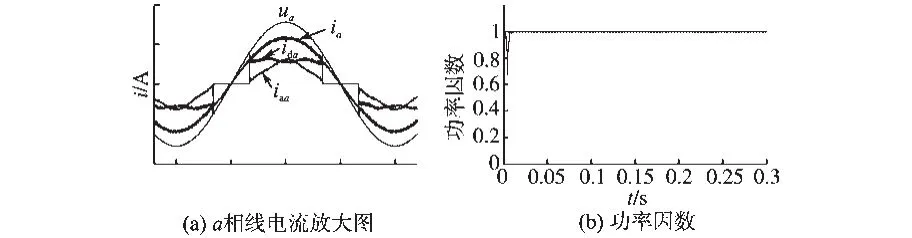
图10 三相混合整流器的a相线电流放大图及功率因数Fig.10 Zoomed-in graph of a phase current and the power factor of HTPVSR

图11 三相混合整流器的交流侧a相电流FFT分析Fig.11 FFT analyses of three-phase hybrid rectifier′s a phase current

图12 HTPVSR在负载扰动情况下的电压波形Fig.12 Voltage waveforms of HTPVSR in situation of load disturbance
4 结论
本文对三相混合电压型整流器提出了改进的拓扑结构和功率分配方法,并基于无源控制理论,提出了基于EL模型和PCHD模型的无源混合控制器。仿真结果表明改进的三相混合整流器在该控制器作用下能够实现网侧电流正弦化、单位功率因数、直流电压恒定控制,并按预设比例进行功率分配,验证了所提控制策略的可行性。
[1]Alves R L,Barbi I.A New Hybrid High Power Factor Three-phase Unidirectional Rectifier[C]//IEEE International Symposium on Industrial Electronics,Montreal,Quebec,Can⁃ada,2006:1046-1051.
[2]Alves R L,Barbi I.Analysis and Implementation of a Hybrid High-power-factor Three-phase Unidirectional Rectifier[J].IEEETransactionsonPowerElectronics,2009,24(3):632-640.
[3]王久和,张巧杰,宋志宏.单向混合三相电压型整流器技术[J].电工技术学报,2015,30(12):68-75.
[4]厍冬瑾,王久和,翟丹丹.一种单向混合三相电压型整流器及其控制[J].电气应用,2015,34(11):138-145.
[5]Soeiro T,Friedli T,Hartmann M,et al.New Unidirectional Hy⁃brid Delta-switch Rectifier[C]//Proceedings of the 37th Annu⁃al Conference of the IEEE Industrial Electronics Society,Mel⁃bourne,Australia,2011:1474-1479.
[6]Thiago B Soeiro,Johann W Kolar.Analysis of High-efficiency Three-phase Two and Three-level Unidirectional Hybrid Recti⁃fiers[J].IEEE Transactions on Industrial Electronics,2013,60(9):3589-3601.
[7]Admarço Vieira Costa,Danillo Borges Rodrigues,Gustavo Bri⁃to De Lima,et al.New Hybrid High-power Rectifier with Re⁃duced THDI and Voltage-sag Ride-through Capability Using Boost Converter[J].IEEE Transactions on Industrial Applica⁃tions,2013,49(6):2421-2436.
[8]Long Bai,Deqiang Wang,Yuanjun Zhou.Study on the Current Control Strategy of Hybrid Rectifier Based on the PR Control⁃ler[C]//International Conference on Electrical Machines and Systems(ICEMS),Busan,Korea(South),2013:1693-1696.
[9]王久和.电能变换器及其无源控制[M].北京:科学出版社,2014.
[10]王久和.电压型PWM整流器的非线性控制[M].第2版.北京:机械工业出版社,2015.
修改稿日期:2016-05-07
Study of Three-phase Bidirectional Hybrid Voltage Source Rectifier with Resistance-inductance Load
SHE Dongjin,WANG Jiuhe,ZHAI Dandan
(College of Automation,Beijing Information Science&Technology University,Beijing,100192,China)
Studied a three-phase hybrid voltage source rectifer with resistance-inductance load.According to the topology,the euler-lagrange mathematical models of boost type DC-DC convertor and PCHD(port control hamiltonation with dissipation)of PWM rectifier were designed.Designed the passive-based controller with PCHD model,which it not only could achieve damping-inject,but also could be energy shaping and be more flexible.Based on the models′passivity,a hybrid control strategy based on PI control on the voltage loop and passive control on the current loop was proposed.The hybrid control strategy is proved feasible by the simulation result in the situation of with resistance-inductance load.
hybrid rectifier;passivity-based control;power distribution;power density
TM461
A
10.19457/j.1001-2095.20161109
国家自然科学基金项目(51477011);北京市自然科学基金重点项目(KZ201511232035);
北京市属高校科技创新能力提升计划项目(TJSHG201310772024);
北京市青年拔尖人才培育计划项目(CIT&TCT201304111)
厍冬瑾(1986-),女,硕士研究生,Email:jade_1228@163.com
2015-09-23
