基于分区变步长爬山法的双馈风机MPPT控制策略
2016-12-06张阁杨艺云肖静高立克肖园园
张阁,杨艺云,肖静,高立克,肖园园
(广西电网有限责任公司电力科学研究院,广西 南宁 530023)
基于分区变步长爬山法的双馈风机MPPT控制策略
张阁,杨艺云,肖静,高立克,肖园园
(广西电网有限责任公司电力科学研究院,广西 南宁 530023)
提出了一种基于分区变步长爬山法的双馈异步风机最大功率点跟踪控制策略,在吸取传统爬山法优点的基础上,给出了一种新的爬山法扰动步长分界方法和整定方案。该策略在风速稳定时能有效地抑制转速的波动,在风速发生变化时能较快地跟踪最大功率点,能有效改善双馈风力发电系统的稳态性能和动态性能。并通过仿真和实验验证了理论分析结果。
双馈风力发电系统;爬山法;变速恒频;最大功率点跟踪
双馈异步风力发电系统具有成本低,风能利用率高,能实现风能的最大功率追踪以及有功、无功功率的独立灵活控制等优点,在当前风力发电市场上占据主导地位[1]。目前双馈风力发电系统的最大风能追踪策略主要有:最佳叶尖速比法、功率信号反馈法、爬山搜索法等[2-3]。相比最佳叶尖速比法和功率信号反馈法,爬山搜索法不需测量风速和已知风机的最大功率曲线,而是通过对发电机转速施加扰动,根据风机输出功率的变化确定发电机转速的控制增量,使风电系统沿功率转速曲线爬行到最大功率点。爬山法能够编程实现且对系统参数依赖度不高,具有自适应性和较高的实用价值。然而传统的定步长爬山法采用固定的转速扰动会导致机组转速波动较大,当风速大幅度变化时也很难快速追踪最优转速,不能及时追踪最大风能[4-6]。
本文提出了一种分区变步长爬山法MPPT控制策略。该策略在吸取传统爬山法优点的基础上,利用函数对风力机的功率-转速曲线进行了分界,在不同的分界区域给出了具体的扰动步长整定方案,并通过仿真和实验进行验证。结果表明,分区变步长爬山法MPPT控制策略相比传统定步长爬山法,在风速稳定时能有效地抑制转速的波动,在风速发生阶跃变化时能较快地跟踪最大功率点,改善了双馈风力发电系统的稳态性能和动态性能。
1 最大功率跟踪原理
根据贝兹理论可知,当风速小于额定风速时,风力机产生的机械功率为

式中:v为风速;S为风力机桨叶扫掠面积;ρ为空气密度;Cp为风能转换系数;β为桨叶节距角;λ为叶尖速比。
其中
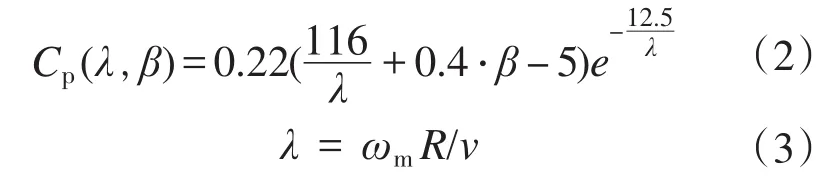
式中:R为叶片半径;ωm为风力机转速。
从式(1)知,风力机从风中吸收的功率P与功率系数 Cp和风速 v的立方成正比。从式(2)和式(3)可知,当 β和v一定时,Cp与ωm呈抛物线关系。因此,当风速v和桨叶节距角 β一定时,风力机输出的功率P只与风机的转速ωm有关。
双馈风力发电机转速与风力机转速的关系如下式:

式中:ω为双馈发电机转速;N为齿轮箱传送比。
由式(4)可知,通过控制双馈发电机转速ω可以间接控制风力机转速ωm。桨叶节距角β一定时,不同风速下风力机输出的功率P与双馈发电机的转速ω的关系曲线如图1所示。
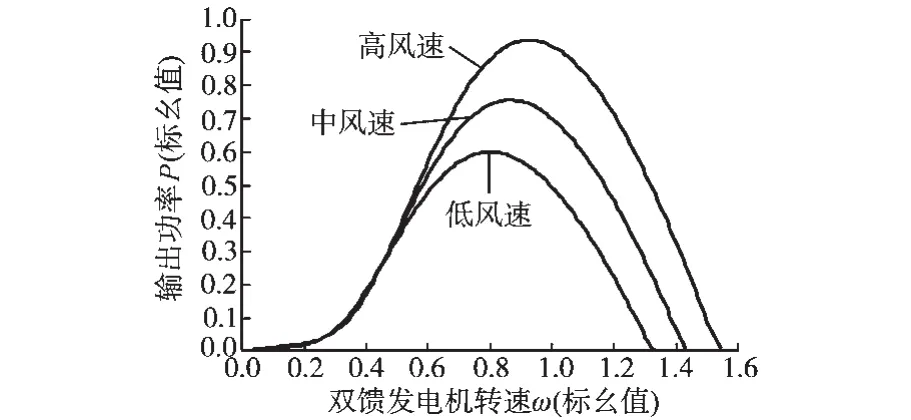
图1 不同风速下P-ω图像Fig.1 Diagram ofP-ωin different wind speeds
由图1可知,当桨叶节距角β一定时,对应每一风速,系统具有唯一的最大功率点。
2 分区变步长爬山法最大功率跟踪算法
通常情况下,传统定步长爬山法的扰动步长的大小很难确定。选择较大的步长有利于在风速发生变化时快速跟踪最大功率点,但在稳态时的转速震荡和功率损耗较大;选择较小的步长在稳态时震荡较小,但又不能满足快速跟踪的要求。
本文提出了一种分区变步长爬山法MPPT控制策略,综合考虑了系统稳态性能和动态性能,可同时实现动态快速响应和稳态振荡较小。
首先建立了分界函数F,F为功率P和功率与转速的导数的绝对值|dP/dω|的乘积。如下式所示:
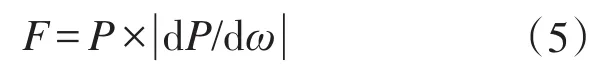
风力机的P-ω曲线与分界函数F如图2所示。
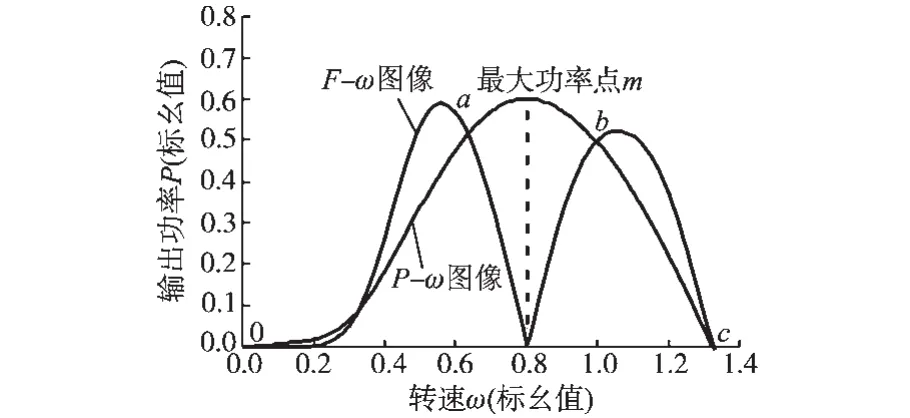
图2 分界函数F图Fig.2 Diagram of partition function F
由图2可知,分界函数F将功率转速P-ω图像分成4部分,分别为oa,am,mb,bc,其中在最大功率点m点附近的am,mb两部分采用变步长模式,距离m点较远的oa,bc两部分采用定步长模式。
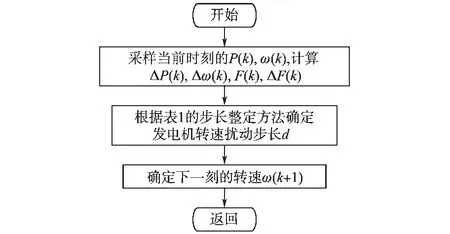
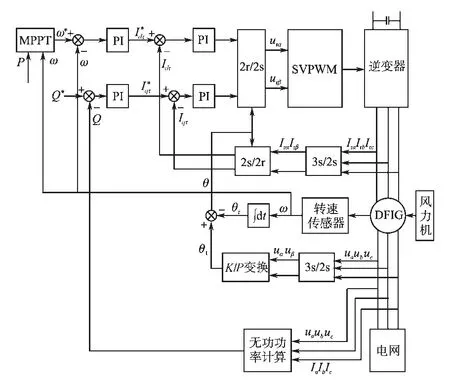
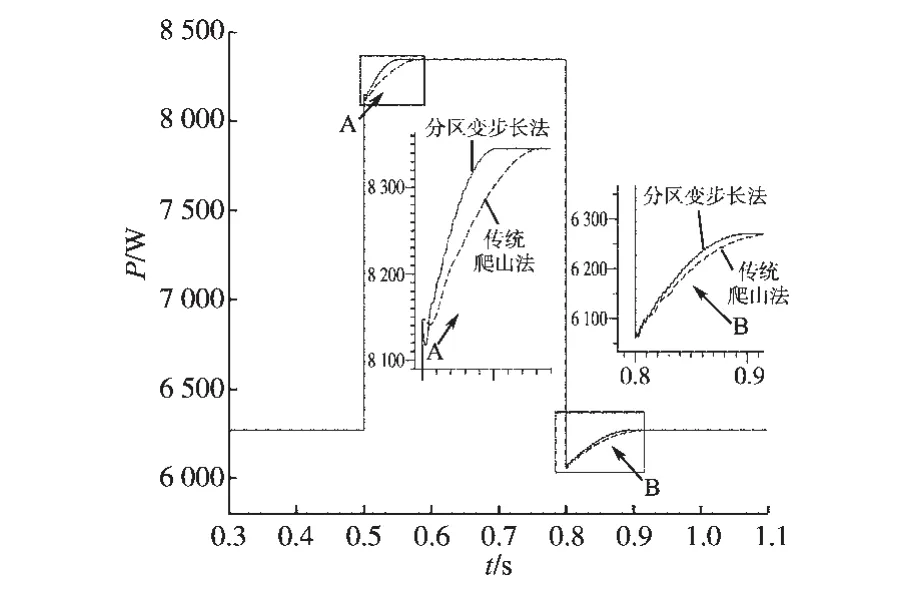
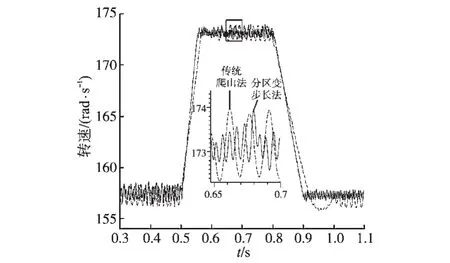
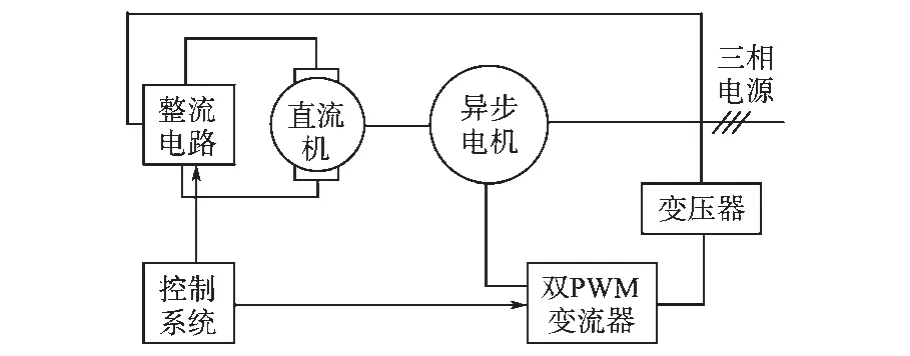
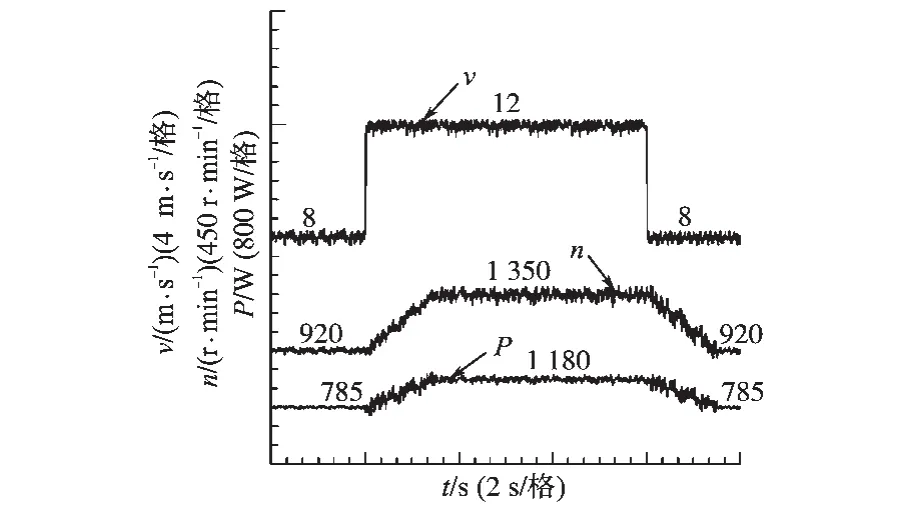
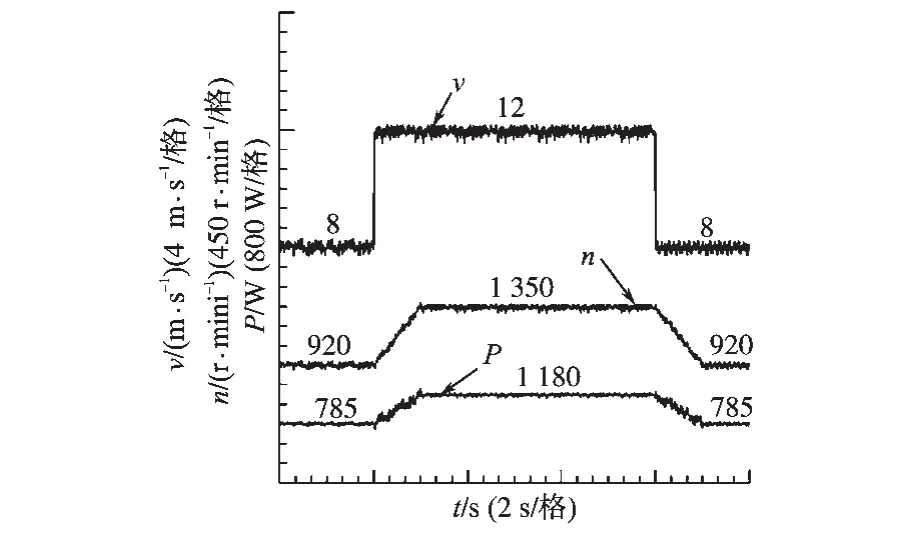
具体步长整定方案如下:选取较大转速扰动定步长d1和d2,分别作用在最大功率点的左侧和右侧,其中d1为正值,d2为负值。在最大功率点m左侧的oa部分,即dF/dω>0或者dF/dω<0且F> P时,采用定步长模式,扰动步长d=d1;在最大功率点m左侧的am部分,即dF/dω<0且F 在不同的分界区域的扰动步长整定模式和步长大小如表1所示。 表1中P为风力机输出功率,F为分界函数,d1和d2分别为最大功率点左侧、右侧的初始扰动步长。 该策略在不同的分界区域采用不同的步长模式和步长大小。系统在风速发生大幅度变化时采用较大的步长,能快速地跟踪最大功率点,在系统工作状态接近最大功率点时,步长逐步减小,并在最大功率点变为零,能有效减小转速震荡和功率损失。分区变步长爬山MPPT算法实现步骤如下: 1)根据所选风机设定最大功率追踪的初始扰动步长d1和d2,二者分别作用于最大功率点左侧和右侧; 2)采样k时刻风力机的输出功率P(k)、发电机转速ω(k); 3)计算相邻两个时刻的风力机输出功率差值ΔP(k)=P(k)-P(k-1)、发电机转速差值Δω(k)= ω(k)-ω(k-1),分界函数 F(k)=P(k)×abs[ΔP(k)/ Δω(k)],F(k)相邻两个时刻的变化量∆F(k)=F(k)-F(k-1); 4)按照表1所示的步长模式和步长大小确定发电机转速的扰动步长d; 5)计算出下一时刻的发电机转速给定值ωref(k+1)=ω(k)+d; 6)重复2)~5)步骤,直到系统工作在最大功率点。 分区变步长爬山MPPT控制算法逻辑图如图3所示。 表1 步长分界整定方法Tab.1 Method of step size partition and tuning 图3 分区变步长爬山MPPT算法逻辑图Fig.3 Improved MPPT algorithm of hill-climbing method based on partition variable step size 本文基于Matlab/Simulink平台搭建了双馈异步风力发电系统的数学模型,采用定子电压定向的矢量控制技术,对双馈发电机进行调速控制,这时双馈风力发电机在两相同步旋转坐标下的数学模型如下: 1)电压方程为 2)运动方程为 3)定子侧功率方程为 式中:ids,iqs分别为定子电流的d,q轴分量;idr,iqr分别为转子电流的d,q轴分量;Uds,Uqs分别为定子电压的d,q轴分量;Udr,Uqr分别为转子电压的d,q轴分量;ω为转子旋转角速度;ωs为转差角速度;Ls,Lr分别为两相旋转坐标系下定子和转子自感;Lm为两相旋转坐标系下定转子绕组间互感;TL为风力机拖动转矩;Ps,Qs分别为定子侧有功、无功功率。 由数学模型方程式(6)~式(8)可得,采用定子电压定向后,实现了转子电流的解耦控制。通过控制双馈发电机转速ω,间接控制与风速相应的风机转速达到最优,从而实现最大功率点追踪(MPPT)。双馈风力发电系统基于定子电压定向的矢量控制原理如图4所示。 图4 双馈风机MPPT控制原理图Fig.4 MPPT control diagram of doubly-fed wind turbine 仿真实验中双馈风力发电系统参数为:额定功率PN=11 kW,额定电压UN=380 V,额定频率fN= 50 Hz,极对数p=2,定子电阻Rs=0.477 Ω,转子电阻Rr=0.431 Ω,定转子间互感Lm=0.052 3 H,定子自感Ls=0.054 H,转子自感Lr=0.053 6 H,摩擦系数F=0.001 N·m·s,转动惯量J=0.330 3 kg·m2。风力机在风速10 m/s时输出的最大功率为6 270 W,在风速11 m/s时输出的最大功率为8 340 W。 两种控制策略的风力机输出功率P如图5所示。发电机转速ωr如图6所示。在t=0.5 s时,风速由10 m/s阶跃至11 m/s,在t=0.8 s时,风速由11 m/s阶跃至10 m/s。 图5 风力机输出功率PFig.5 Output power P of wind turbine 图6 发电机转速ωFig.6 Generator rotating speedω 由图5可知,在风速发生阶跃变化时,分区变步长法相比传统爬山法,风力机的输出功率P跟踪最大功率点的速度更快。由图6可知,在风速发生阶跃变化时,分区变步长法相比传统爬山法,发电机转速ω能更快趋于稳定,且在稳态时的震荡较小。 利用直流电机和绕线式异步发电机搭建双馈风力发电系统的实验平台。仿真参数如下:直流电机额定功率3 kW,额定电压220 V,励磁电压220 V,额定电流18 A,额定转速1 500 r/min。异步机额定功率3 kW,额定频率50 Hz,额定定子电压380V,极对数p=2。实验平台结构如图7所示。 图7 双馈风力发电系统实验平台结构图Fig.7 Diagram of DFIG power generation experimental platform 风速发生阶跃变化时的实验结果如图8和图9所示。 图8 传统爬山法实验结果图Fig.8 Experimental result of traditional hill-climbing method 图9 分区变步长爬山法实验结果图Fig.9 Experimental result of hill-climbing method based on partition variable step size 对比图8和图9可知,当双馈风力发电系统的风速从8 m/s阶跃到12 m/s时,分区变步长爬山法能及时跟踪最大功率点,且相比于传统爬山法,跟踪最大功率所用的时间更短,稳态时的转速波动也较小。 本文讨论了一种基于分区变步长爬山法的双馈风力发电系统MPPT控制策略,分析了传统定步长爬山法和分区变步长爬山法的原理,提出了一种新的爬山法—扰动步长分界法和整定方案,并通过仿真和实验对提出的MPPT策略进行了验证。 实验结果表明:与传统定步长爬山法相比,分区变步长爬山MPPT控制策略在风速稳定时能有效地抑制转速的波动,在风速发生阶跃变化时能较快地跟踪最大功率点,有效地改善了双馈风力发电系统的稳态性能和动态性能。本文提出控制策略对在实际应用中提高风能的转化效率具有重要参考意义。 [1]苏立峰.风电发展现状与潜力分析探讨[J].能源与节能,2013,12(99):72-74. [2]罗承先.世界风电发展现状与前景预测[J].中外能源,2012,17(3):24-31. [3]Henk P,Peter T.Comparison of Direct-drive and Geared Gen⁃erator Concepts for Wind Turbines[J].IEEE Trans.on Ener⁃gy Conversion,2006,21(3):725-733. [4]Wang Q,Chang L.An Intelligent Maximum Power Extraction Algorithm for Inverter-based Variable Speed Wind Turbine System[J].IEEE Trans on Power Electonics,2004,19(5):1242-1249. [5]Abdullah M A,Tan C W.A Review of Maximum Power Point Tracking Algorithms for Wind for Wind Energy Systems[J].Renewable and Sustainable Energy Reviews,2012,16(5):3220-3227. [6]程启明,程尹曼,王晓雯,等.风力发电系统技术的发展综述[J].自动化仪表,2012,33(1):1-8. [7]唐友军.小型风力发电系统最大功率点跟踪研究[D].武汉:武汉科技大学,2013. [8]吴政球,干磊,曾议,等.风力发电最大风能追踪综述[J].电力系统及其自动化学报,2009,21(4):88-93. [9]钟沁红,阮毅,赵梅花,等.双馈风力发电转子侧PWM变换器功率控制策略[J].电机与控制应用,2012,39(12):46-50. [10]彭国平,李帅,鱼振民,等.小型风电系统最大功率跟踪的研究[J].西安交通大学学报,2004,38(4):357-360. [11]Qu K Q,Li J.A MPPT Vector Control Method for Wind Power PMSG System[J].IEEE Trans.on Power Electronics,2012,2(2):1264-1267. 修改稿日期:2016-03-21 Research on MPPT Control Strategy of Doubly-fed Wind Turbine Based on Partition Variable Step Size Hill-climbing Method ZHANG Ge,YANG Yiyun,XIAO Jing,GAO Like,XIAO Yuanyuan Presented a doubly-fed asynchronous wind turbine MPPT control strategy based on partition variable step size hill-climbing method,this strategy had absorbed the advantages of the traditional climbing method,gave a new step dividing method and tuning scheme.The partition variable step size hill-climbing MPPT control strategy could effectively suppress the fluctuation of the rotation speed when the wind speed was stable,and could track the maximum power point quickly when the wind speed was changed,the steady performance and dynamic performance of the doubly-fed wind power generation system could be effectively improved.The theoretical analysis results are verified by simulation and experiment. doubly-fed wind power generation system;hill-climbing method;variable speed with frequency constant;maximum power point tracking TM614 A 10.19457/j.1001-2095.20161112 广西电网有限责任公司科技项目(GXKJ00000006) 张阁(1987-),男,硕士,工程师,Email:zhangge0708@126.com 2015-10-13
3 仿真及结果分析
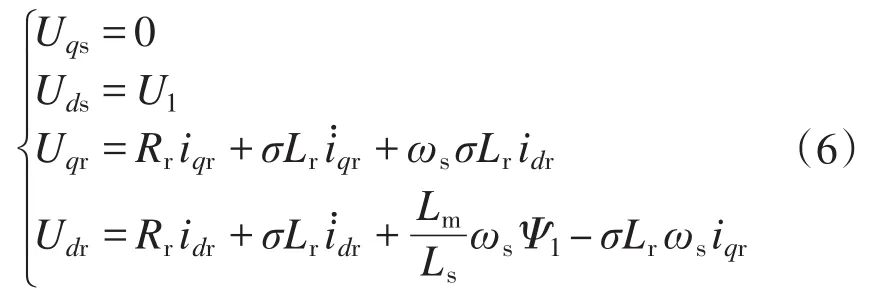
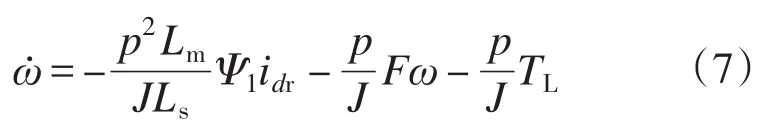
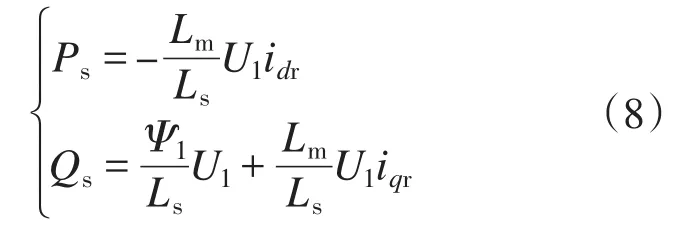
4 实验及结果分析
5 结论
(Guangxi Power Grid Electric Power Research Institute,Nanning 530023,Guangxi,China)
