一类三阶半线性中立型阻尼微分方程的振动性

林文贤

(韩山师范学院 数学与统计学院，广东 潮州 521041)



一类三阶半线性中立型阻尼微分方程的振动性

林文贤

(韩山师范学院 数学与统计学院，广东 潮州 521041)

研究一类三阶非线性中立型阻尼泛函微分方程,利用广义Riccati变换和积分平均技巧, 建立了保证该类方程的一切解振动或者收敛于零的若干新的充分条件, 推广和改进最近文献的结果.

三阶中立型方程；阻尼项；Philos型振动性

0 引言

众所周知,作为简谐振荡的数学模型,二阶常微分方程的所有解都有任意大的零点,从而是振动的.而更一般的,描述电子和机械振荡的数学模型是泛函微分方程,其振动性研究在实际和理论中都有着重要意义.近年来,泛函微分方程的振动理论受到极大关注,可以参看文献[1-18].但是与一阶和二阶方程相比,关于三阶微分方程的振动性文献就少得多,而关于三阶中立型方程的振动结果则更少. 最新的成果可以参看文献[19-30].

本文将考虑如下的一类具阻尼项的三阶半线性中立型泛函微分方程[r(t)([x(t)+p(t)x(τ(t))]″)α]′+m(t)([x(t)+p(t)x(τ(t))]″)α+ʃbaq(t,ξ)xα[g(t,ξ)]dσ(ξ)=0

(1)

的振动性,其中α是两个正奇整数之比.在本文中假设下列条件成立：

(H1)r(t)∈C([t0,+∞),(0,+∞)),p(t),m(t)∈C([t0,+∞),R+),R+=[0,+∞)，0≤p(t)≤p<1,且

(H3)g(t,ξ)∈C([t0+∞)×[a,b],R+);g(t,ξ) ≤t,ξ∈[a,b];g(t,ξ)分别关于 t, ξ 非减, 并且

(H4)σ(ξ)∈C([a,b],R)为非减.(1)中的积分为Stieltjes积分.

定义函数

y(t)=x(t)+p(t)x(σ(t)).

(2)

称方程(1)的解是指函数x(t)∈C1[Tx,∞),Tx≥t0,使得r(t)[y″(t)]α∈C1[Τx,∞]且在[Τx,∞]上满足方程(1). 本文只考虑方程(1)满足性质Sup{|x(t)|:t≥T}>0对一切T≥Tx成立的解.方程(1)的一个解称为振动, 如果它在[Τx,∞]上有任意大的零点. 否则, 称它为非振动.

文献[26]给出了方程(1)当m(t)=0,α=1时的特殊情形的一切解振动或者收敛于零的充分条件,文献[27]给出了方程(1)当α=1时的特殊情形的一切解振动或者收敛于零的充分条件.我们的目的是利用广义Riccati变换和积分平均技巧建立使得方程(1)的一切解振动或收敛于零的充分条件,推广和包含文[26-27]的结果.

1 若干引理

引理1 设x(t)是方程(1)的最终正解, 则由(2)定义的y(t)只能有下列两种类型

(A)y(t)>0,y′(t)>0,y″(t)>0; (B)y(t)>0,y′(t)<0,y″(t)>0;

对t≥t1成立, 其中t1充分大.

证明 设x(t)是方程(1)的最终正解及条件(H3),存在t1≥t0,当t≥t1时,有x(t)>0,x(σ(t))>0,x(g(t))>0,易知,y(t)>x(t)>0且

[r(t)(y″(t))α]′+m(t)(y″(t))α≤-ʃbaq(t,ξ)xα[g(t,ξ)]dσ(ξ)<0,

则

在[t2,t]上对上式积分有

在上式中令t→∞,利用(H1),有y′(t)→-∞,因此y′(t)最终为负.但是,由y′(t)和y″(t)最终为负,可知y(t)最终为负,此与y(t)>0的假设矛盾,故有y″(t)>0.因此y(t),只能有(A)和(B)两种类型.

引理2 设x(t)是(1)的正解,而相应的y(t)具有(B)型. 如果

(3)

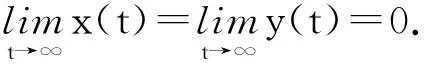
x(t)=y(t)-p(t)x(τ(t))>L-py(τ(t))≥L-p(l+ε)=K(L+ε)=K(L+ε)>Ky(t),

(4)

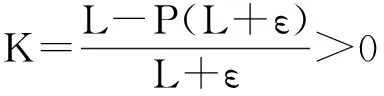
[r(t)(y″(t))α]′+m(t)(y″(t))α≤-Kαʃbaq(t,ξ)yα[g(t,ξ)〗)dσ(ξ)，

注意到(H3)和y(t)是(B)型, 得到

[r(t)(y″(t))α]′+m(t)(y″(t))α≤-Kαyα[g(t,b)]ʃbaq(t,ξ)dσ(ξ)≡-q1(t)ya[g1(t)]，

(5)

[z(t)r(t)(y″(t))α]′(r(t)y″(t)z(t))′≤-q1(t)yα(g1(t))z(t),

(6)

从t到∞对式(6)积分产生

r(t)(y″(t))αz(t))′≥ʃ∞tq1(s)y[g1(s)]z(s)ds,

利用yα[g1(t)]≥Lα,z′(t)>0,有

(7)

再对式(7)从t到∞积分,得到

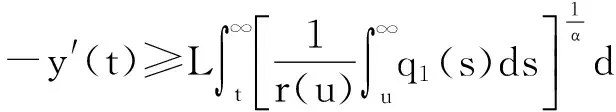
将上式从t1到∞积分,有

人生在世，都要经历漂泊，都要经受苍茫和困惑。这样的时候，仪式感就是闪烁在人性河道上的灯塔，它总是以它的精神内涵照彻混沌，点拨人心。人类的卑微和伟大，常常是通过仪式才得以充分凸显出来的。

引理3[31]设

u(t)>0,u′(t)>0,u″(t)≤0,t≥t0,

则对任一θ∈(0,1)存在Tθ≥t0,使得

引理4[32]设

u(t)>0,u′(t)>0,u″(t)>0,u‴(t)≤0,t≥Tα,

则存在β∈(0,1)和Tβ≥Τθ, 使得u(t)≥βtu′(t),t≥Tβ.

引理5[33]设A>0,B>0,X≥0, 则有

2 主要结果

下面利用Philos型的积分平均条件[34],给出方程(1)的新的振动结果.为此引进如下一类函数X. 令

D={(t,s)|t≥s≥t0}, D0={(t,s)|t>s≥t0}.

函数H(t,s)∈C(D，R)称为属于X 类, 记作H∈X, 如果满足

(ⅰ)H(t,t)=0,t≥t0;H(t,s)>0,(t,s)∈D0;

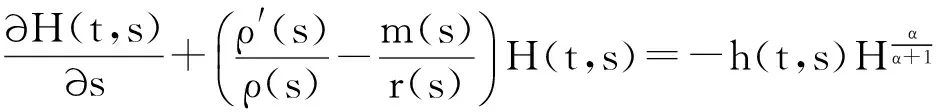
定理1 设(3)成立, 且存在函数H∈X和ρ∈C1([t0,∞),(0,∞)),使得

(8)

其中

(9)

这里的α和β由引理3和引理4定义, 则方程(1)的每一解x(t)振动, 或者当t→∞时x(t)→0.

证明 设方程(1)存在非振动解x(t),不失一般性,设x(t)最终为正(当x(t)最终为负时可以类似地证明),故存在充分大的t1≥T(T在引理1中提及).使得当t≥t1时有x(t)>0,x(σ(t))>0,x(g(t))>0.下面针对(2)式定义的函数y(t)进行讨论.由引理1可知,y(t)可能为型(A)或(B)型.

首先,设y(t)为(A)型,有

x(t)=y(t)-p(t)x(σ(t))≥y(t)-py(t)≥(1-p)y(t).

由(H3)和(1), 得到

[r(t)(y″(t))α]′+m(t)(y″(t))α≤-(1-p)αʃbaq(t,ξ)yα[g(t,ξ)]dσ(ξ)≤

-(1-p)αyα[g(t,a)]ʃbaq(t,ξ) dσ(ξ)≡-q2(t)yαg(t,a)，

(10)

其中

q2(t)=(1-p)αʃbaq(t,ξ) dσ(ξ).

(11)

令

(12)

则有

在引理3中,令u(t)=y′(t),则有不等式

利用引理4得到

y[g(t,a)]≥βg(t,a)y′[g(t,a)].

因此有

(13)

其中Q(t)由(9)和(11)定义.

令

由(13)得到

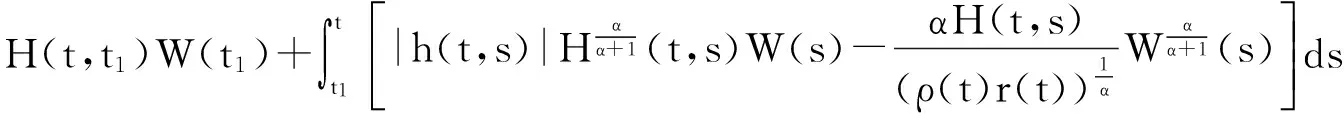
(14)

取

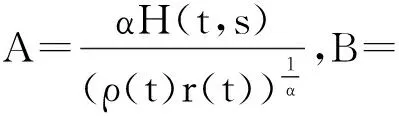
利用引理5,有

则由(14)产生

或者

(15)

易知,式(15)与条件(8)矛盾,故情形(A)不出现.

注:若取H(t,s)=(t-s)n, 则定理1的Philos型条件简化为Kamenev型条件.H的其他选择如下：

3)H(t,s)=-(et-s-es-t)n；

更一般地有

[1]R.P.Agarwal,S.R.GraceandD.O’Regan,OscillationTheoryforDifferenceandFunctionalDifferentialEquations[M].Dordrecht:KluwerAcademicPublishers, 2000.

[2]R.P .Agarwal, S.R. Grace and D. O’Regan, Oscillation Theory for Second Order Dynamic Equations[M].London: Taylor & Francis Group , 2003.

[3]林文贤.具连续分布滞量的二阶中立型方程的振动性定理[J].应用泛函分析学报, 2003，5 (2)：174-177.

[4]林文贤.一类非线性偶数阶中立型方程的振动准则[J].工程数学学报,2005, 22(1):159-162.

[5]林文贤.一类中立型泛函微分方程的振动准则[J].数学的实践与认识,2005,35(6)，211-215.

[6]林文贤.一类具连续分布滞量的偶数阶微分方程的新振动性定理[J].辽宁师范大学学报(自然科学版)，2006，29(4),394-396.

[7]林文贤. 一类具连续偏差变元的二阶非线性中立型方程的振动性[J].西南师范大学学报(自然科学版),2009, 34(4):1-3.

[8]Lin Wenxian. Interval oscillation theorems for certain second order neutral differential equations with continuous deviating arguments[J].Southeast Asian Bulletin of Mathematics, 2010,34(6):1055-1061.

[9]林文贤.具有阻尼项的中立型Emden-Fowler方程的区间振动准则[J].韩山师范学院学报,2011, 32(6):8-11.

[10]Lin Wenxian. A note on oscillation of certain second order partial functional differential equation with damping [J].Pioneer Journal of Mathematics and Mathematics Sciences, 2012,4(1):125-128.

[11]林文贤.具连续分布时滞的二阶半线性中立型阻尼泛函微分方程的Philos型振动定理[J].韩山师范学院学报,2012, 33(3):7-12.

[12]林文贤.一类二阶中立型微分不等式最终正解的不存在性[J].河南师范大学学报(自然科学版),2012,40(2)：31-33.

[13]林文贤.二阶中立型阻尼微分不等式最终正解不存在性[J].兰州理工大学学报，2012，38(5)：138-140.

[14]林文贤.具连续偏差变元的二阶阻尼微分方程的振动性[J].中国科学院研究生院学报，2012，29(5)：594-598.

[15]林文贤.一类中立型阻尼泛函微分方程的振动性[J].四川师范大学学报(自然科学版),2013, 36(3):20-22.

[16]林文贤.一类带强迫项的二阶阻尼微分方程的区间振动性[J].郑州大学学报(理科版),2014, 46(2):1-5.

[17]林文贤,俞元洪.高阶中立型时滞微分方程的振动准则[J].应用数学学报,2014, 37(6):1018-1024.

[18]林文贤. 振动性和周期解理论的研究[M].北京:国防工业出版社,2014.

[19]L.H. Erbe, Q.Kong and B.G.Zhang, Oscillation Theory for Difference and Functional Differential Equations[M].New York: Marcel Dekker, 1995.

[20]Aktas M.F.,Tiryaki A, Zafer A. Oscillation criteria for third order nonlinear functional differential equations[J].Appl. Math. Letters, 2010(23):.756-762.

[21]Dzurina J. Asymptotic properties of the third order delay differential equations[J].Nonlinear Anal TMA, 1996(26):33-43.

[22]Grace S.R. Agarwal R.P, Pavani R, et al. On the oscillation criteria for third order nonlinear functional differential equations[J].Appl. Math. Comput., 2008(202)：102-112.

[23]Grace S.R. Agarwal R.P, Aktas M F. On the oscillation of third order functional differential equations[J].Indian J Pure Appl. Math., 2008(39):491-507.

[24]Parhi N, Padhi S. On asymptotic behavior of solutions of third order delay differential equations[J].Indian J Pure Appl. Math., 2002(33):327-332.

[25]Q.X. Zhang, L. Gao & Y.H. Yu, Oscillation criteria for third-order neutral differential equations with continuously distributed delay[J].Applied Mathematics Letters, 2012(25): 1514-1519.

[26]俞元洪.三阶中立型分布时滞微分方程的振动定理[J].琼州学院学报, 2010, 17(5): 1-5.

[27]林文贤.三阶中立型分布时滞阻尼微分方程的振动定理[J].琼州学院学报，2014，21(2) : 7-11.

[28]林文贤.一类三阶中立型阻尼方程的Philos型振动定理[J].宁夏大学学报(自然科学版),2014, 35(2):1-4.

[29]林文贤.三阶非线性中立型阻尼泛函微分方程的振动性[J].安徽大学学报(自然科学版),2015, 39(3):5-9.

[30]林文贤.一类具分布时滞的三阶非线性泛函微分方程的振动性和渐近性[J].韩山师范学院学报,2015，36(3) :6 -14.

[31]Erbe L. Oscillation criteria for second order nonlinear delay equations[J].Canad Math. Bull., 1973(16): 49-56.

[33]Hardy G H，Litterwood J E，Polya G.Inequalities(2nd Edition) [M].Cambridge: Cambridge University Press, 1952.

[34]Ch G Philos. Oscillation theorems for linear differential equation of second order[J].Arch Math., 1989(53): 483-492.

(编校：吴炎)

Oscillation for Third-Order Neutral Functional Differential Equations with a Damping Term and Distributed Delays

LIN Wen-xian

(College of Mathematics and Statistics, Hanshan Normal University, Chaozhou Guangdong 521041，China)

The oscillation of third-order nonlinear neutral damped functional differential equations with distributed delays was studied. By using a generalized Riccati transformation and integral averaging technique, established is some new sufficient conditions which insure that any solution of this equation oscillates converges to zero. Consequently, the corresponding results in the latest literature are extended and improved.

a damping term ; third-order neutral equations; Philos-type oscillation

2016-04-12

广东省高等学校特色创新项目(2014GXJK125);广东省高等教育教学改革项目(GDJG20142396)

林文贤(1966- ),男,广东潮州人,韩山师范学院数学与统计学院教授,研究方向为泛函微分方程理论及应用.

O175.10

A

1008-6722(2016) 05-0038-06

10.13307/j.issn.1008-6722.2016.05.08