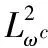Studies on the Volterra Integral Equation with Linear Delay
2017-09-03-
-
(Colloge of Mathematics and Statistics, Hanshan Normal University, Chaozhou 521041, China)
Studies on the Volterra Integral Equation with Linear Delay
ZHENGWei-shan*
(Colloge of Mathematics and Statistics, Hanshan Normal University, Chaozhou 521041, China)
This paper is concerned about the Volterra integral equation with linear delay. First we transfer the integral interval [0,T] into interval [-1, 1] through the conversion of variables. Then we use the Gauss quadrature formula to get the approximate solutions. After that the Chebyshev spectral-collocation method is proposed to solve the equation. With the help of Gronwall inequality and some other lemmas, a rigorous error analysis is provided for the proposed method, which shows that the numerical error decay exponentially in the innity norm and the Chebyshev weighted Hilbert space norms. In the end, numerical example is given to confirm the theoretical results.
Chebyshev spectral-collocation method; linear delay; Volterra integral equations; error analysis
The Volterra integral equation with linear delay is as follow:
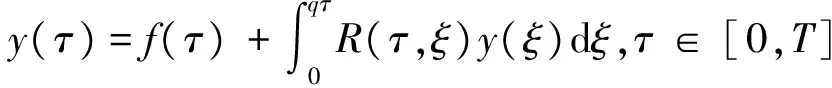
(1)
where the unknown functiony(τ) is defined on [0,T],T<+∞ andqis constant with 0 Equations of this type arise as models in many fields, such as the Mechanical problems of physics, the movement of celestial bodies problems of astronomy and the problem of biological population original state changes. They are also applied to network reservoir, storage system, material accumulation, different fields of industrial process etc, and solve a lot problems from mathematical models of population statistics, viscoelastic materials and insurance abstracted. The Volterra integral equation with linear delay is one of the important type of Volterra integral equations with great significance in both theory and applications. There are many methods to solve Volterra integral equations, such as Legendre spectral-collocation method[1], Jacobi spectral-collocation method[2], spectral Galerkin method[3-4], Chebyshev spectral-collocation method[5]and so on. In this paper, inspired by[5] and [6], we use a Chebyshev spectral-collocation method to solve Volterra integral equations with linear delay. (2) Then equation (1) becomes and the above equation can be rewritten as follows. (3) Obviously, the above equations hold atximentioned above,xi∈[-1,1]. Thus, we have (4) Using aN+1-point Legendre quadrature formula (2), corresponding weightwk, we can obtain that (5) 2.1ConvergenceanalysisinL∞(-1,1)space Theorem1Supposeu(x)istheexactsolutiontoequations(3)anduN(x)istheapproximatesolutionobtainedbyusingtheChebyshevspectralcollocationmethod.ThenforNsufficientlylarge,weget (6) where ProofMinusing(4)by(5)gives Notee(x)=u(x)-uN(x), then we have (7) By Theorem 4.3, 4.7 and 4.10 in [7], we get |J1(x)|≤CN-m|K(x,·)|Hm,N(-1,1)‖uN(sx(·))‖L2(-1,1). (8) u-uN+INu-u=e(x)+INu-u. (9) Now we are in the position to estimate the above inequality term by term. Firstly the second conclusion in Theorem 1.8.4 in [8] shows that (10) For the estimation of ‖INJ1‖L∞(-1,1), firstly using the first inequality in (8), we obtain CN-mK*(‖e‖L∞(-1,1)+‖u‖L∞(-1,1)). Then, due to Theorem 3.3 in [9], we have ‖INJ1(x)‖L∞(-1,1)≤‖IN‖L∞(-1,1)‖J1(x)‖L∞(-1,1)≤ CN-m(logN)K*(‖e‖L∞(-1,1)+‖u‖L∞(-1,1)). For ‖J3(x)‖L∞(-1,1), applying (7) and lettingm=1, we get From what discussed above, we can see Since This completes the proof of this theorem. Theorem2Supposeu(x)istheexactsolutiontoequation(3)anduN(x)istheapproximatesolutionobtainedbytheChebyshevspectralcollocationmethodwhichdefinedin(5).ThenforNsufficientlylarge,weget ProofAsthesameprocedureinthedeductionfrom(7)to(9)inTheorem1,wecanderivethefollowinginequality Further more applying the generalized Hardy’s inequality with weights[10], we get Now we estimate each item from left to right for the above inequality. ForJ0(x), the first conclusion in Theorem 1.8.4 in [8] shows that (11) By Theorem 1 in [11] and (8), we get Due to the conclusion in Theorem 1, we get (12) The corresponding exact solution is given byu(x)=e4x,x∈ [-1,1]. a.The errors u-uN in L∞ and norms. b.The comparison between approximate solution uN and the exact solution u.Fig.1 Numerical results N68101214L∞⁃error0.0300419.0557×10-42.4424×10-55.6363×10-79.5384×10-9L2ωc⁃error0.0287919.2524×10-42.4507×10-55.2913×10-78.6576×10-9N1618202224L∞⁃error1.2083×10-101.1866×10-122.1316×10-141.4211×10-147.1054×10-15L2ωc⁃error1.0916×10-101.1034×10-128.6652×10-148.3351×10-149.2255×10-15 [1] TANG T, XU X, CHENG J. On Spectral methods for Volterra integral equation and the convergence analysis[J]. J Comput Math, 2008,26(6):825-837. [2] CHEN Y, TANG T. Convergence analysis of the Jacobi spectral-collocation methods for Volterra integral equation with a weakly singular kernel[J]. Math Comput, 2010,79(269):147-167. [3] WAN Z, CHEN Y, HUANG Y. Legendre spectral Galerkin method for second-kind Volterra integral equations[J]. Front Math China, 2009,4(1):181-193. [4] XIE Z, LI X, TANG T. Convergence analysis of spectral galerkin methods for Volterra type integral equations[J]. J Sci Comput, 2012,53(2):414-434. [5] GU Z, CHEN Y. Chebyshev spectral collocation method for Volterra integral equations[J]. Contem Math, 2013,586:163-170. [6] LI J, ZHENG W, WU J. Volterra integral equations with vanishing delay[J]. Appl Comput Math, 2015,4(3):152-161. [7] CANUTO C, HUSSAINI M, QUARTERONI A,etal. Spectral method fundamentals in single domains[M]. New York: Spring-Verlag, 2006. [8] SHEN J, TANG T. Spectral and high-order methods with applications[M]. Beijing: Science Press, 2006. [9] MASTROIANNI G, OCCORSIO D. Optional system od nodes for Lagrange interpolation on bounded intervals[J]. J Comput Appl Math, 2001,134(1-2):325-341. [10] KUFNER A, PERSSON L. Weighted inequality of Hardy’s Type[M]. New York: World Scientific, 2003. [11] NEVAI P. Mean convergence of Lagrange interpolation[J]. Trans Amer Math Soc, 1984,282:669-698. (编辑 HWJ) 2016-10-29 国家自然科学基金资助项目(11626074);韩山师范学院创新强校项目(Z16027);中山大学广东省计算科学重点实验室开放基金资助项目(2016011);韩山师范学院扶持项目(201404) O242.2 A 1000-2537(2017)04-0083-06 带线性延迟项的Volterra积分方程研究 郑伟珊* (韩山师范学院数学与统计学院, 中国 潮州 521041) Chebyshev谱配置方法; 线性延迟项; Volterra型积分方程; 误差分析 10.7612/j.issn.1000-2537.2017.04.014 *通讯作者,E-mail:weishanzheng@yeah.net1 Chebyshev spectral-collocation method



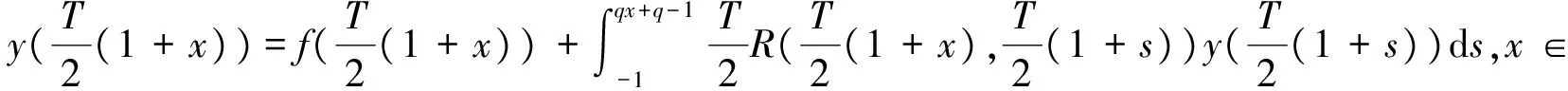
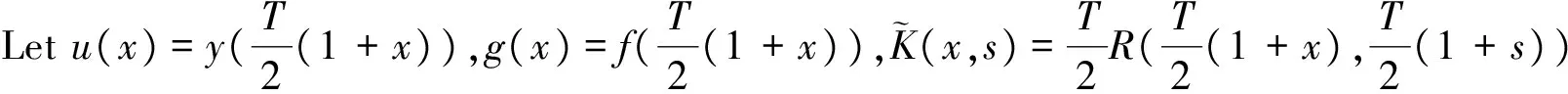
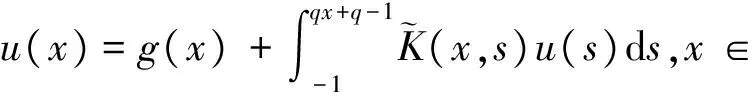
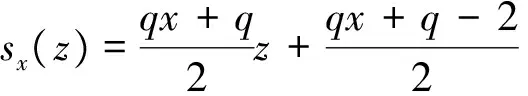
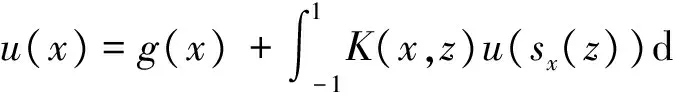
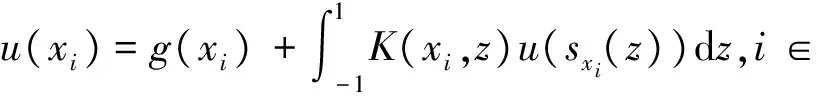
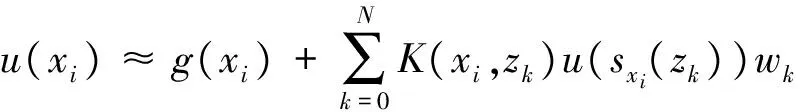
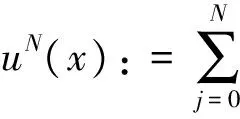
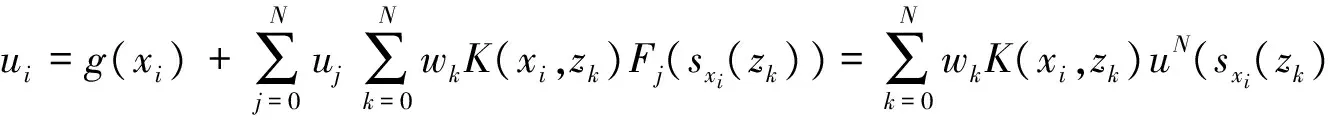
2 Convergence analysis

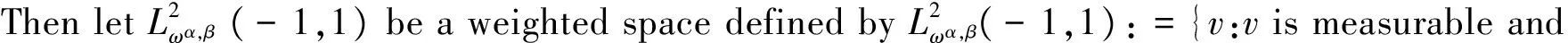
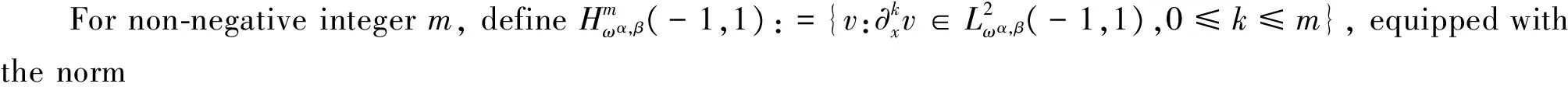
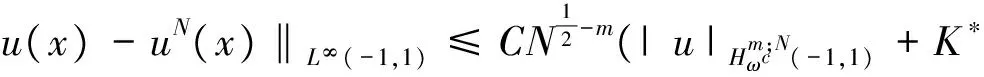
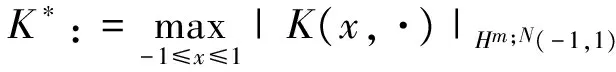
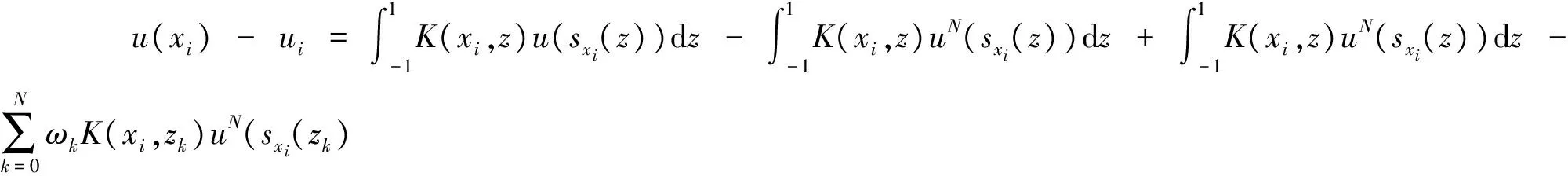



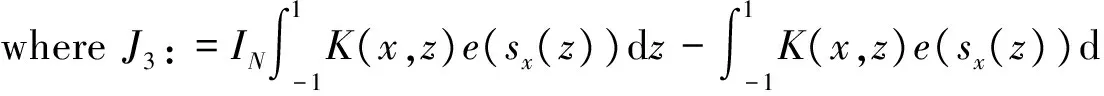

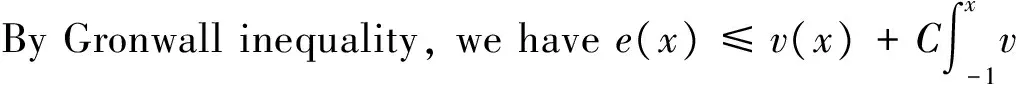

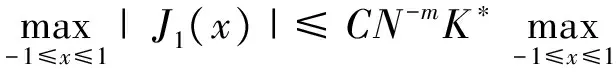

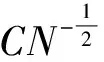


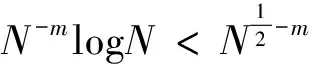
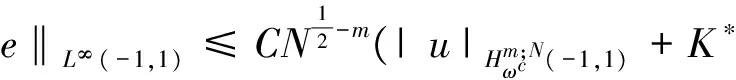

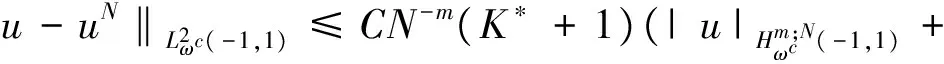
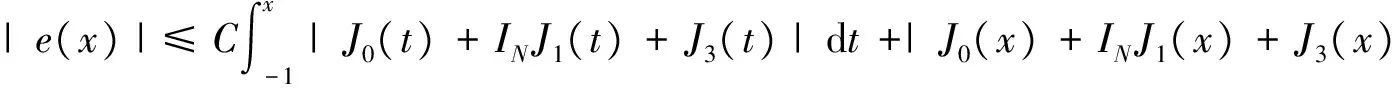
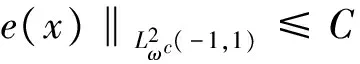

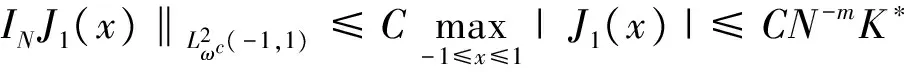
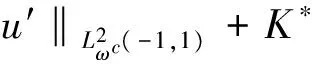
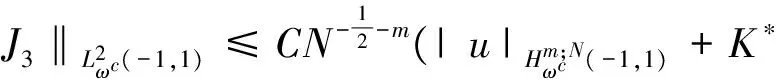
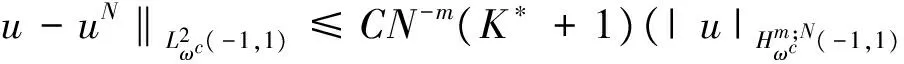
3 Algorithm implementation and numerical experiment