磁瓦机械手交流伺服装置的建模及特性分析
2016-12-06江顺友舒志兵曹海笑
江顺友, 舒志兵, 曹海笑
(1.南京工业大学 自动化与电气工程学院,江苏 南京 211816;2.路斯特传动系统(上海)有限公司,上海 200137)
磁瓦机械手交流伺服装置的建模及特性分析
江顺友1, 舒志兵1, 曹海笑2
(1.南京工业大学 自动化与电气工程学院,江苏 南京 211816;2.路斯特传动系统(上海)有限公司,上海 200137)
研究磁瓦生产过程中与压机配套使用的专用机械手,介绍了机械手伺服系统建模的方法,将四阶模型化简为二阶模型,建立了磁瓦机械手数学模型,并在MATLAB中对系统进行动态特性分析。通过实验研究,得出系统超调量小,上升时间比较短,动态特性良好,可以达到系统测试的标准,为磁瓦机械手伺服系统的调试提供了可靠依据。
磁瓦;交流伺服;建模;仿真;机械手
0 引 言
磁瓦是电机中的重要组成部分,主要用在永磁直流电机中,目前大部分磁性材料厂家都是24小时连续生产,利用人工来手动完成磁瓦的生产,生产效率低下,劳动强度大,质量不够稳定,对生产工艺的管理也带来很大难度。磁瓦机械手可以提高磁性材料厂家的自动化水平,降低劳动者劳动强度,且磁性材料行业的专用机械手的需求量缺口较大。采用全伺服驱动的专用机械手在国内需求量较高,通过研究伺服系统的建模方法与机械手的数学模型,以解决机械手设计与测试过程中的系统性能进行分析,为磁性材料行业专用机械手控制系统的研发工作提供方法。
1 机械手交流伺服系统建模
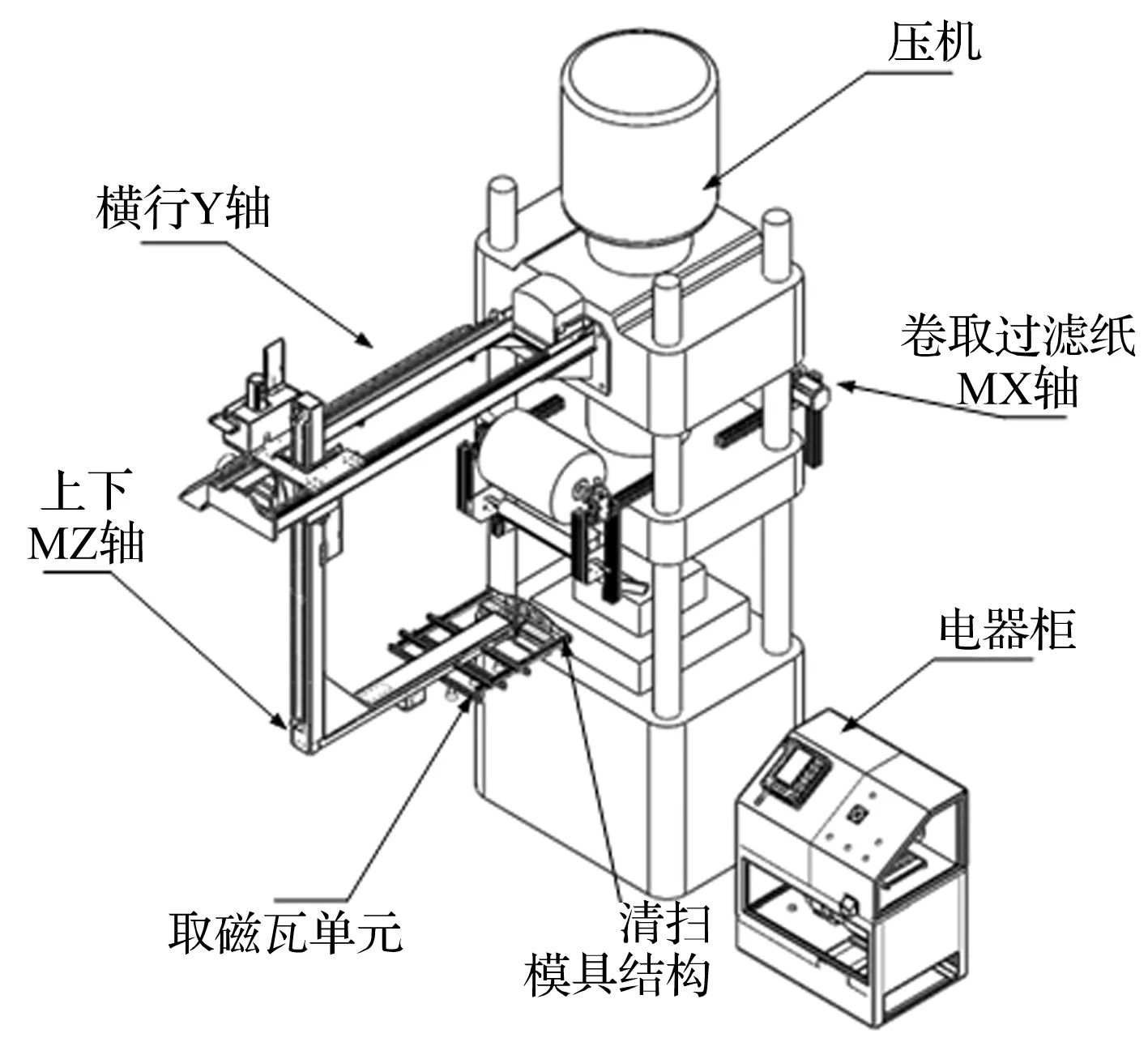
图1 磁瓦机械手结构设计简图
如图1所示,伺服控制系统是磁瓦机械手的重要组成部分,伺服系统的性能优劣直接影响取磁瓦的质量和精度。机械手系统的数学模型主要包括两个部分[1]:一部分是伺服驱动部分(包括驱动器和伺服电机),另一部分是机械传动系统(包括机械传动及执行部件)。根据机械动力学原理,对磁瓦伺服机械手系统总结归纳,得到如下动力学方程[2]:
(1)
(2)
(3)
其中JD为电机的转动惯量;TD为电机的转矩;JF为负载的转动惯量;DF为粘性摩擦因数;TF为机械平台在电机侧的反作用力;Ni为变速比;θD为电机转动角度;θF为负载端轴转动角度;KF为连接机械部分和电机轴的弹性常数。
对公式(1)、(2)、(3)进行Laplace变换,求出传递函数如下:
(4)
(5)
(6)
综合公式(4)、(5)和(6),可以求得磁瓦机械手伺服系统模型,采用比例控制策略,设计系统控制器,得到从输入变量U(s)到输出变量θF(s)的模型方框图,如图2所示。
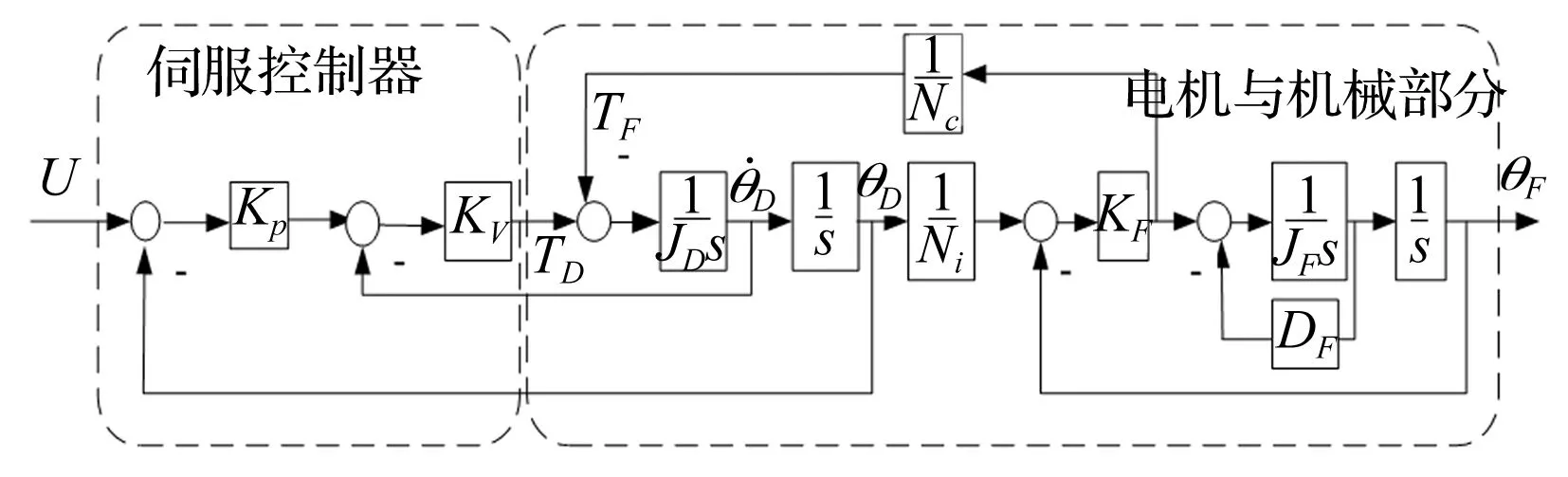
图2 磁瓦机械手伺服装置的四阶模型
根据梅森公式分析,由图2得到如图3所示的信号流图。
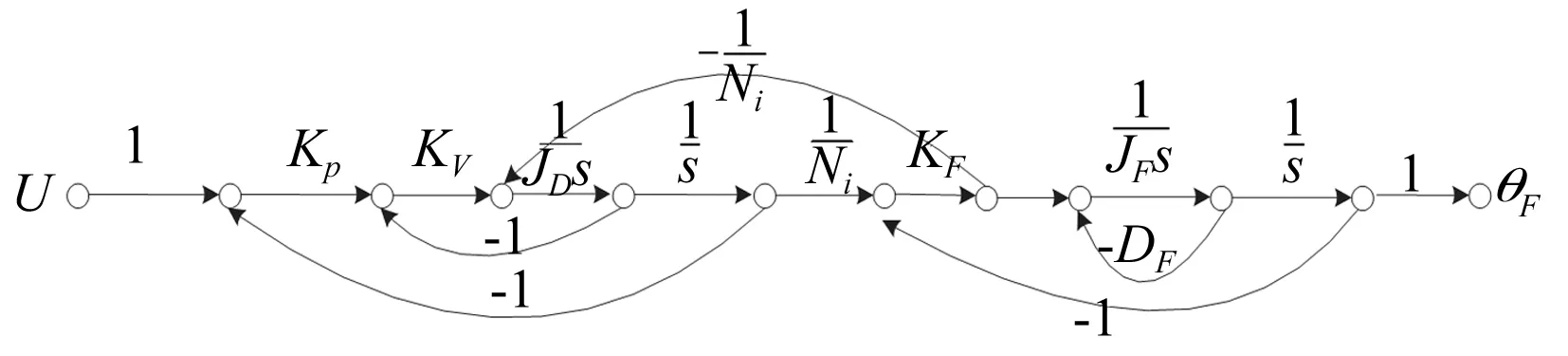
图3 磁瓦机械手模型对应的信号流图
其中有五条回路,没有不接触回路,分别为:
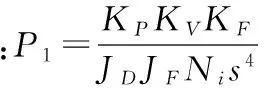
流图余因子式:Δ1=1
根据以上信息,求出系统输出与输入端传递函数表达式为:
所以系统的最终闭环传递函数化简为:
(7)
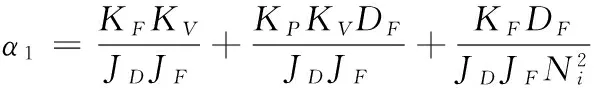
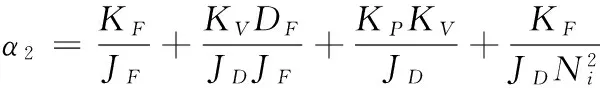
公式(7)中,待求参数主要包括:位置回路增益KP和速度放大增益KV。假定系统电机转轴总的转动惯量为Jtotal,则:
(8)
(9)
根据机械设计原理,机械系统的固有频率ωF和相对阻尼比ζF表示如下:
(10)
(11)
一般在描述机械部分特性时,经常用ωF和ζF代替DF,KF和JF,因为,我们在描述机械性时,通常用固有频率ωF和相对阻尼比ζF来计算。
但是,由于机械部分的固有频率主要依赖于它的大小和质量,而标准伺服参数的确定并不是基于ωF的,所以,位置环增益KP和速度环增益KVelocity也可以由机械系统的固有频率ωF来表示:
KP=cPωF
(12)
KVelocity=cVωF
(13)
其中cP,cV的最优值选择,通过文献[3]可知:
四阶系统:cP=0.24,cV=0.82;二阶系统:cP=0.2304,cV=0.96。
(14)
式中
β0=(1+NF)cPcV;β1=(1+NF)(cV+2cPcVζF)+2NFζF;
β2=(1+NF)(1+2cVζF+cPcV);β3=2ζF+(1+NF)cV
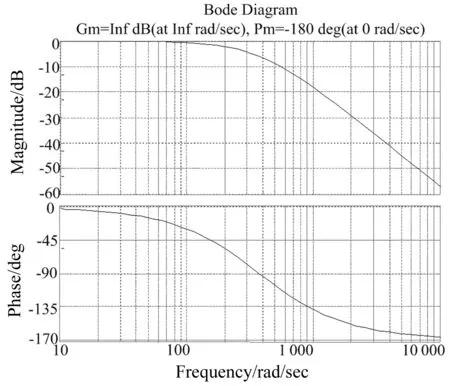
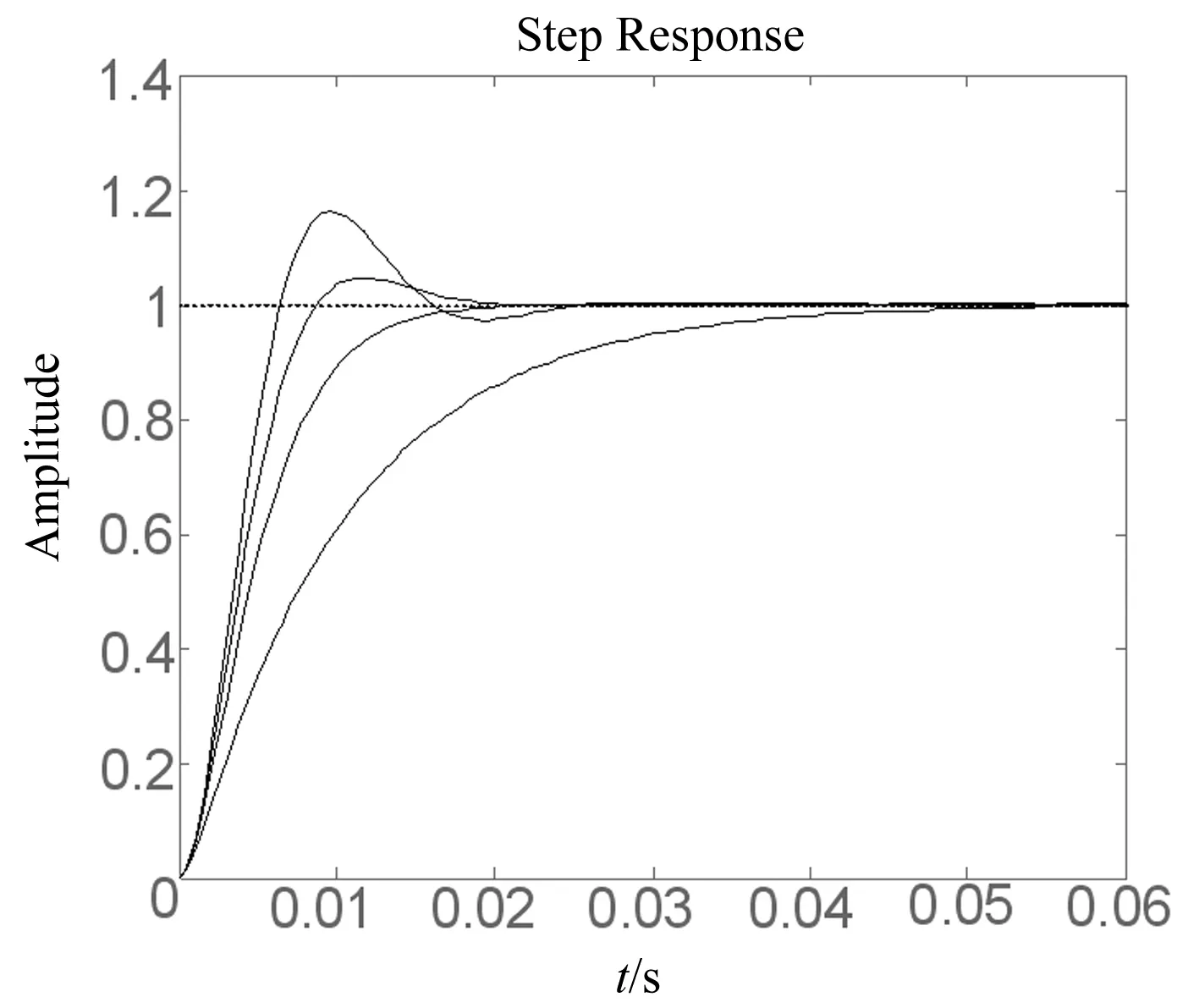
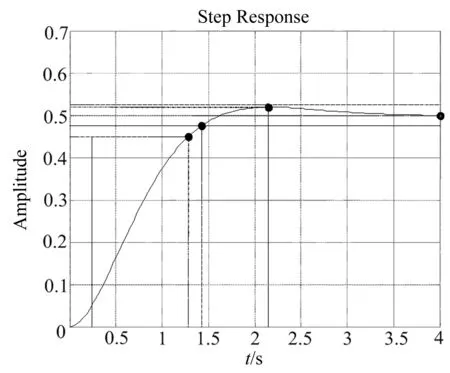
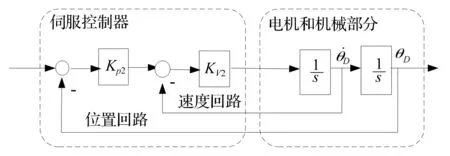
其中在电机选型时,参数NF必须满足0 通过上述简化过程,最终只要确定负载转动惯量JF、粘性摩擦因数DF、柔性变形系数KF和电机的转动惯量JD这四个参数就可以计算出系统传递函数。 鉴于机械手伺服系统由很多模块组成,各部分受到多种因素影响,具有非线性及各种相关关系,实际控制系统十分复杂。所以在设计控制器时,一般需要忽略一些次要因素把某些性能理想化,用低阶模型来简化控制器设计。本文所研发的磁瓦机械手在机电结构上是一个两维数控系统,考虑到本设计中机械手的控制系统只有编码器作为反馈装置,是半闭环系统,所以可以对推导的四阶模型进行降阶处理。 由图4可得到磁瓦机械手伺服系统的二阶传递函数: 图4 磁瓦机械手伺服系统的二阶模型 (15) 上式(15)中,KP2为位置回路比例增益,KV2为速度控制回路增益。根据文献[3],得到比例增益系数: KP2=cP2ωF,KV2=cV2ωF; cP2≈cP=0.24,cV2≈4cP=0.96 这样通过求取ωF的值,就可以得到磁瓦机械手交流伺服系统的二阶和四阶传递函数。 根据公式(13)所示的传递函数模型,机械手伺服系统模型参数取决于机械手系统自身的机械特性。确定了JD,JF,KF,DF这四个参数,即可以确定齿轮齿条伺服系统的数学模型。 要确定磁瓦机械手伺服系统的系统参数,首先必须确定整个伺服系统的机电结构参数。采用齿轮齿条结构,通过齿轮减速和齿条传动后带动相应轴做往复运动。结构上相对简单,主要由上下部(Z轴)和横出横进部(Y轴)组成,Z轴和Y轴均采用伺服电机控制。磁瓦机械手伺服系统Z轴和Y轴的机电结构如图5所示。 机械设计部分参数如下(以Z轴为例):Z轴齿轮的齿数Z=38,长度L=27.63 mm,外直径D=80.88 mm,负载重量m=3.5 kg。Z轴所用减速器是台湾精锐Apex行星减速器,型号:AB115-R-010,减速比N=10。减速器的转动惯量IS=2.57 kg·cm2,重量7.8 kg,效率≥97%。根据机械设计手册[4-5]: (1)计算齿轮的转动惯量: (16) 式中ρ为材料密度; D为圆柱体的外直径; L为圆柱体的长度。 由于齿轮是钢结构,密度ρ=7 850 kg/m3,由公式(16)求出齿轮转动惯量:I=9.11 kg·cm2 (2)计算负载到减速机的转动惯量公式为: IL=m×(D/2)2 (17) 由公式(17)求出Z轴的负载转动惯量IL=57.27 kg·cm2。 (3)减速机到电机的转动惯量公式为: (18) 式中N为减速比; e为机械效率; IL→M为折合到电机轴的负载转动惯量; IF为负载总转动惯量(等于齿轮转动惯量加负载转动惯量)。 JF=IS×N2+IF (19) (20) 由公式(19)、(20)运算得: JF=IS×N2+I+IL=323.38kg·cm2 (4)惯性比NF (5)求系统的固有频率和阻尼比 钢与钢的摩擦因数[5-6]DF=0.2,KF=20 000。经过公式(10)、(11)的运算,此时Z轴的固有频率ωF和阻尼比ζF为: 根据以上计算,磁瓦机械手控制系统的阻尼比,满足0≤ζF≤0.02的约束。 (6)确定传递函数 求得参数ωF和ζF以后,以及获知CP、CV的值和惯量比NF之后,根据公式(14)、(15)便可求出Z轴齿轮齿条伺服系统的四阶模型和二阶模型的传递函数为: (21) (22) 同样的原理也适用于Y轴,也可求得Y轴伺服系统的四阶模型和二阶模型的传递函数。 4.1 频率响应分析 图6 系统对数频率特性曲线 频率响应反映了正弦信号作用下系统响应的性能,具有物理意义鲜明,计算量小、直观性强等优点。系统的幅值和相角直接由margin( )函数求得。利用传递函数,在MATLAB中可以得到,磁瓦机械手控制系统的系统频率特性曲线图,如图6所示。 4.2 控制系统稳定性分析 稳定是控制系统能够运行的首要条件,若系统的极点都在左半平面,则可以判定该系统是稳定的[7]。利用MATLAB能很方便地求出系统的零极点,从而实现控制系统的稳定性以及最小相位系统的判断。在MATLAB中建立M文件,程序运行结果表明:系统都是负极点,系统是稳定的,是最小相位系统。 4.3 系统的时域特性分析 图7 系统在阻尼变化时的单位阶跃响应曲线 机械手在运行过程中,由于机械系统的阻尼受部件材料、结构、质量等的影响,在整个伺服系统的运动过程中是变化的,这就使系统的性能在原有基础上会出现一定程度的偏差。随着阻尼系数的增大,磁瓦机械手伺服系统的伺服刚度降低,阻尼系数过大或过小,容易造成不稳定。图7为系统在不同的阻尼ξ下变化时的阶跃响应曲线。 时间响应主要研究系统在一定输入信号的作用下,其输出信号在时域内的变化情况。众所周知,阶跃函数是最典型的输入作用信号。通过绘出系统的阶跃响应曲线,分析系统的动态性能指标,MATLAB[8]绘制出磁瓦机械手控制系统的阶跃响应曲线如图8所示。 由图8可知,系统的动态性能指标具体如下: 最大偏移量h(tp)=0.519;终值h(∞)=0.5;峰值时间tp=2.1 ms; 图8 系统阶跃响应曲线 超调量σ%=3.7%;上升时间tr=1.1 ms;调节时间ts=1.4 ms。 上述六个动态性能指标,基本可以体现系统动态过程的特征。由磁瓦机械手伺服控制系统的对数频率特性曲线和阶跃响应曲线,可以知道系统超调量小,上升时间比较短,动态特性良好,可以达到系统测试的标准,为磁瓦机械手伺服系统的调试提供了可靠依据。 [1] 李宁,陈桂.运动控制系统[M].北京:高等教育出版社,2004. [2] 吴世名.基于ARM的三轴机械手控制系统研究与设计[D].浙江:浙江工业大学,2013. [3] NAKAMURA M,GOTO S, KYURA N. Mechatronic servo system control [M]. Berlin, New York: Springer-Verlag, 2004. [4] 王爱玲.现代数控机床[M]. 北京: 国防工业出版社,2009. [5] 唐金松.简明机械设计手册[M].上海:上海科学技术出版社,2009. [6] 成大先.机械设计手册[M].北京:化学工业出版社,2004. [7] CHOY RON EDELMAN.Parallel MATLAB:doing it right[J].Proceedings of the IEEE,2005,(6):331-341. [8] 李维波.MATLAB在电气工程中的应用[M].北京:中国电力出版社,2007. Modeling and Characteristic Analysis of the AC Servo Device of the Magnetic Shoe Manipulator Jiang Shunyou1, Shu Zhibing1, Cao Haixiao2 (1.College of Automation and Electrical Engineering, Nanjing University of Technology, Nanjing Jiangsu 211816, China;2. Lust Servo Systems (Shanghai) Co., Ltd., Shanghai 200137, China) This paper studies the special manipulator used in combination with the press in the process of production of magnetic shoes. It presents the modeling method for the manipulator servo system and builds up a mathematical model for the manipulator of the magnetic shoe by simplifying the four-order model into a two-order model. Furthermore, it uses MATLAB to make a dynamic characteristic analysis on the system. Through experimental study, we find the system has small overshoot, short rise time and excellent dynamic characteristics, and can meet the system test requirements, thus providing a reliable basis for the debugging of the servo system of magnetic shoe manipulator. magnetic shoe;AC servo;modeling; simulation;manipulator 10.3969/j.issn.1000-3886.2016.03.003 TP273 A 1000-3886(2016)03-0007-04 江顺友(1990-),男,江苏连云港人,硕士生,主要研究方向:运动控制技术、数控系统、机电一体化。 舒志兵(1965-),男,江苏南京人,副教授,南京工业大学运动控制研究所所长,主要研究方向:交流伺服系统、DSP技术、现场总线、数控系统、运动控制、机电一体化系统等。 定稿日期: 2015-09-102 机械手交流伺服系统模型简化
3 磁瓦机械手齿轮齿条伺服系统模型参数确定
4 磁瓦机械手交流伺服系统动态仿真