Delta并联机器人抓放轨迹优化

李云辉

(中国科学院长春光学精密机械与物理研究所，吉林 长春 130033)



Delta并联机器人抓放轨迹优化

李云辉

(中国科学院长春光学精密机械与物理研究所，吉林 长春 130033)

在Delta并联机器人门形抓放轨迹的基础上，阐述了采用正弦修正梯形加速度曲线进行轨迹规划和门形路径合成的方法。从减小机构震动和冲击的角度出发，以降低Delta机器人主动臂驱动轴端的最大角加速度为目标，对门形轨迹的相关运行参数进行了优化。针对正弦修正梯形加速度曲线规划方式中运动始末端存在跃度突变，导致柔性冲击的问题，提出了改进型的正弦修正梯形加速度曲线，使得整个运行周期内跃度曲线变得连续，消除了系统的柔性冲击。

Delta机器人；轨迹规划；路径合成；参数优化；柔性冲击

0 引 言

与串联结构机器人相比，Delta并联机器人具有刚度好、惯量小、位置精度高等优点，适合于完成生产线上快速地物体抓放动作，代替手工操作，提高生产效率[1-2]。

为加快Delta并联机器人的抓放速度，其运动的加速度通常很大，不可避免的会引入机械震动和冲击，既对运动精度带来影响，又加快了机械结构的老化和磨损。为减小机构的震动冲击，同时降低抓放周期，需要合理规划Delta机器人的运动轨迹。传统机器人通常采用梯形、多项式、修正梯形等加速度曲线进行轨迹规划[3-5]，这些方式较适用于单一直线运动，而Delta机器人多采用的门形轨迹可分解为竖直、水平和竖直三个直线运动，因此如何将这三部分进行合理运动衔接和参数整合优化，是影响Delta机器人运动路径优化的关键因素。本文在Delta并联机器人门形抓放运动轨迹的基础上，在不增加运行周期的前提下，以降低Delta机器人主动臂最大角加速度为目标，对其轨迹路径进行了优化选择。

1 Delta机器人抓放轨迹设计

1.1 轨迹参数

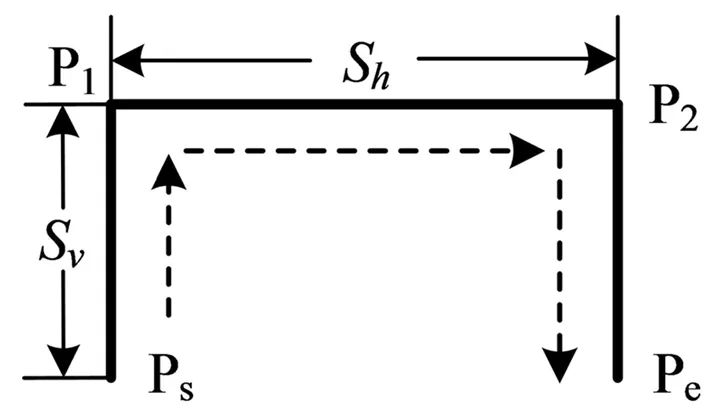
图1 Delta机器人门形运动轨迹

Delta并联机器人通常用于完成生产线上的高速抓取—放置操作，理论上只需完成从抓取点到放置点的直线运动，但实际应用中为躲避障碍物，其运动路径多为门形，如图1所示。

图1中Ps为抓取点，Pe为放置点，Delta并联机器人按图中虚线箭头所示方向运动。完成一次抓放操作的门形轨迹参数包括：壁障高度Sv，水平运动距离Sh。其中，壁障高度Sv取决于抓取物体的尺寸，通常为固定值；水平运动距离Sh取决于机器视觉系统实时给定的抓取点与放置点的坐标数据。

1.2 轨迹规划

为保证Delta机器人抓放操作快速、平稳，没有刚性冲击，本文中采用正弦修正梯形加速度曲线函数，其函数表达式为[6-7]：

(1)

其中am为最大加速度，T为运动周期，T1、T2、T3、T4为中间时间点。

以t=0和t=T时刻的速度及加速度等于零为前提条件，对式(1)加速度曲线进行两次积分，得到位移曲线表达式[6-7]：

(2)

其中P1、P2、P3、P4分别为：

由式(2)可知：位移s是最大加速度am、运行周期T及参数T1、T2、T3、T4的函数，为减少变量数目，设定T1=0.125T、T2=0.375T、T3=0.625T、T4=0.875T。将一段轨迹的总位移S及运行周期T代入式(2)中，便可得到：

(3)

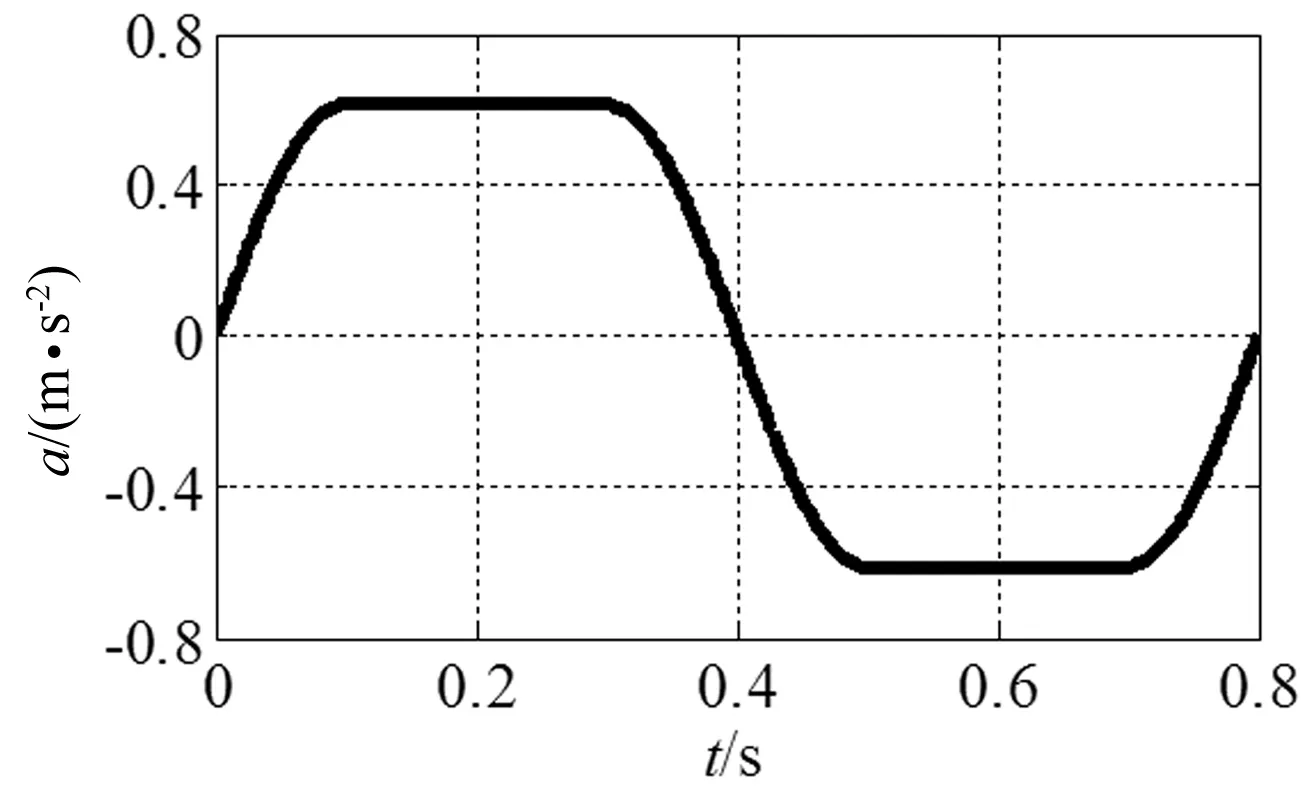
图2 加速度a随时间t的变化曲线

图3 位移s随时间t的变化曲线

通过式(3)可以计算得到最大加速度am，再将其代入式(1)与式(2)中，即可分别得到加速度a与瞬时位移s随时间t的变化曲线，如图2、图3所示。

1.3 路径合成

由图1中可以看出，Delta机器人完成一次抓放操作的门形轨迹可以分解为三段直线运动。对每段直线运动均进行上述的正弦修正梯形加速度曲线规划，设竖直运动的运行周期为Tv，水平运动的运行周期为Th，则整个抓放操作的运行时间为：

T=2×Tv+Th

(4)

图4 Delta机器人平滑过渡门形路径

但在工程应用中，为避免Delta机器人在门形路径转角处产生的冲击震动，通常在转角处引入平滑过渡曲线。一种方法就是在转角附近进行竖直运动和水平运动的时间耦合，如图4所示，实线部分为实际运动轨迹，实际竖直运行壁障高度为Sva。

具体实现过程为：Delta机器人抓起物体后，首先竖直向上运动，待运动到壁障高度Sv后，记为t1时刻，启动水平运动，此时运动为竖直运动与水平运动的合成；运行到Tv时刻，变为水平运动，至(T-Tv)时刻，又启动竖直向下运动，水平运动和竖直运动合成为平滑过渡曲线，(T-t1)时刻至T时刻为完全的竖直运动。整个运行周期变为：

T=2×t1+Th

(5)

2 Delta机器人运行轨迹优化

Delta机器人完成一次抓放的运行周期是影响生产效率的关键因素。为减少运行周期，通常需以更大的加速度运行，而加速度的增大必然导致电机输出转矩增大、电机容量需求增大，系统震动冲击增加等不良后果。因此下面讨论在相同运行周期前提下，如何通过对抓放轨迹的优化，降低Delta机器人主动臂电机轴端的最大加速度。

表1 Delta机器人结构尺寸参数

以表1中的结构参数为例进行分析，设定门形轨迹的壁障高度Sv=30 mm，抓取点Ps和放置点Pe的坐标分别为(-100,0,0)和(100,0,0)，即水平移动距离Sh=200 mm。按1.3节中的路径合成方式，需已知竖直运动距离Sva和水平运动距离Sh，竖直运动时间Tv和水平运动时间Th。以上参数中Sh已知，因此对空间轨迹造成影响的主要是Tv、Th及Sva(Sva≥Sv)。

图5 Delta机器人空间运行轨迹

图5为设定参数Tv=0.2 s、Th=0.3 s、Sva=60 mm时合成的门形运行路径。采用文献[6]中介绍的位置逆解方式，将合成路径中随时间变化的空间位置逆向解算为三个驱动轴的转角位置，进而求得轴端的角速度、角加速度及跃度曲线，如图6所示。

图6 Delta机器人轴端角度、角速度、角加速度及跃度曲线

以上述参数为基准进行轨迹优化，经计算，Delta机器人运动到壁障高度Sv的时刻t1=0.1 s，将其代入到式(5)中，可以得到整个运行周期T=0.5 s。

在保证运行周期T=0.5 s不变的前提下，固定参数Th，通过改变Tv和Sva得到一组仿真数据，如表2所示；同理固定参数Tv，得到表3数据；固定参数Sva，得到表4数据。由表2可知：为保证运行周期T不变，Tv与Sva须同向变化，在Tv=0.2 s、Th=0.3 s、Sva=60 mm点得到最大加速度的极小值；同理，观察表3和表4中的数据，同样在Tv=0.2 s、Th=0.3 s、Sva=60mm点得到最大加速度的极小值。综合表2～表4可知：在门形轨迹参数为Sv=30 mm、Sh=200 mm条件下，轨迹参数取Tv=0.2 s、Th=0.3 s、Sva=60 mm时可以得到最优轨迹，其电机输出轴端的最大加速度为75.46 rad/s2。

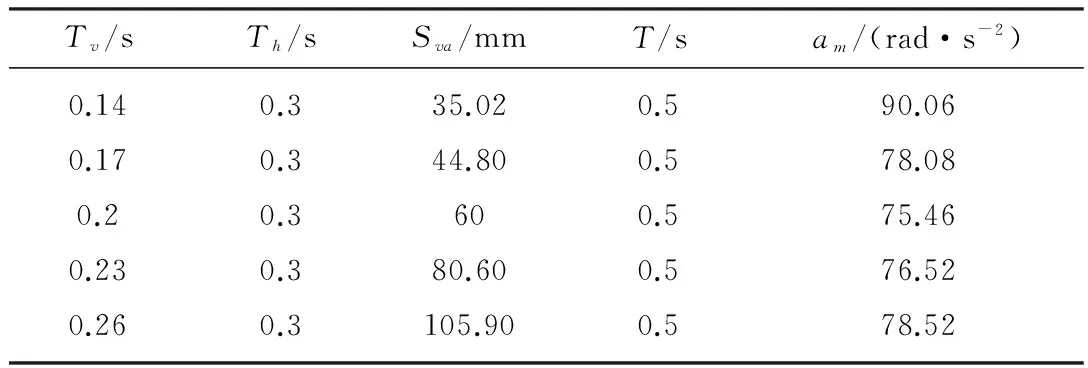
表2 参数Th固定时的仿真数据

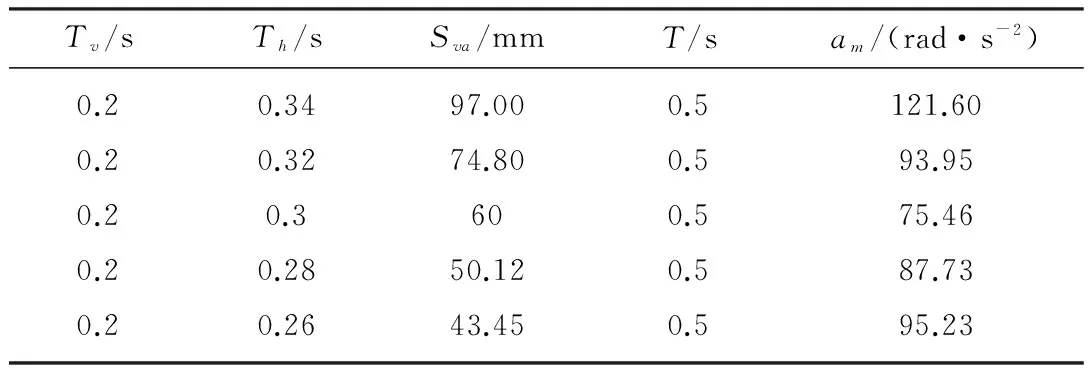
表3 参数Tv固定时的仿真数据

Delta机器人在实现抓放操作的过程中，通常需要机器视觉系统进行实时目标位置给定，但一般情况下其抓放轨迹参数变动不大。因此，可以常用轨迹位置参数为基准，通过上述方式计算得到最优轨迹参数，即Tv、Th、Sva，将其直接应用于Delta机器人轨迹规划算法中，避免因实时复杂的优化算法带来实时性的问题。

表4 参数Sva固定时的仿真数据

3 始末端柔性冲击的消除

采用1.2节介绍的正弦修正梯形加速度曲线可以保证Delta机器人在整个轨迹运行过程中快速、平稳，没有刚性冲击。对正弦修正梯形加速度曲线进行求导，便可得到对应的跃度曲线，可以发现在运行起始点和终止点的跃度存在突变，这会带来柔性冲击，给系统带来不利影响。

(6)

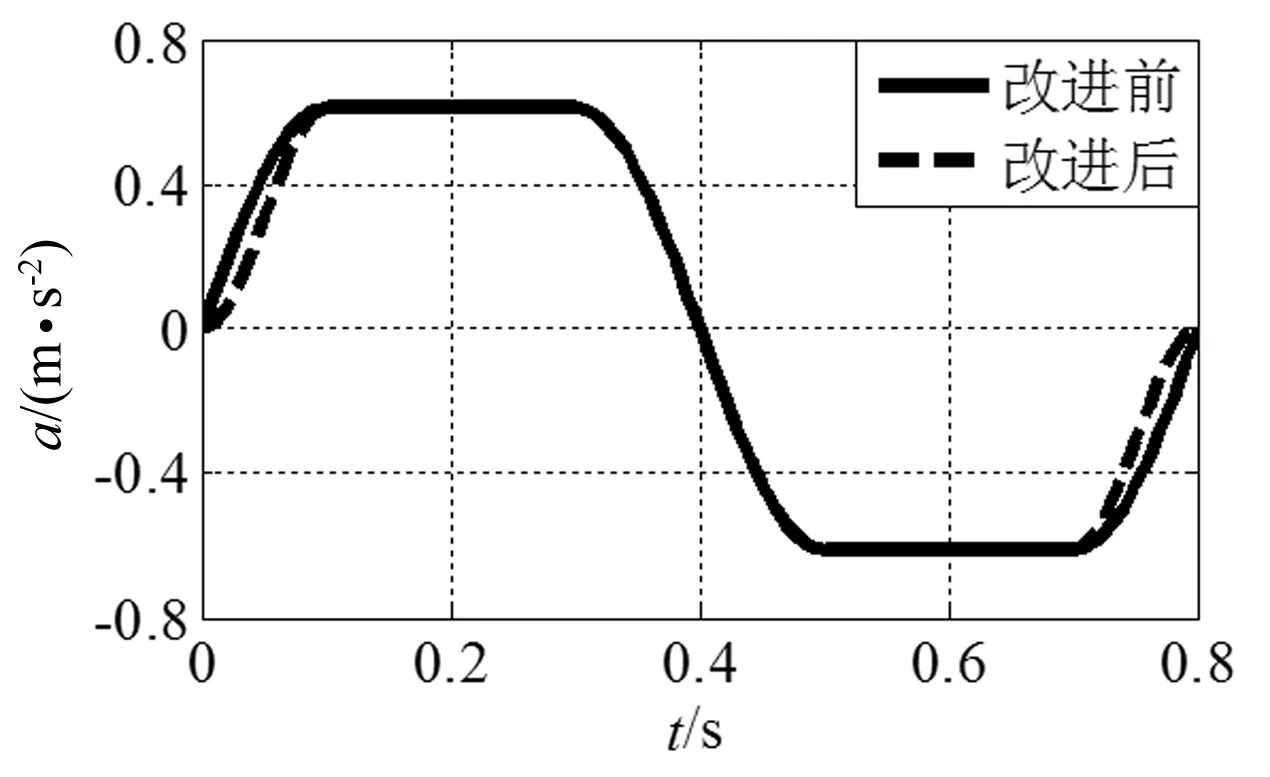
图7 正弦修正加速度曲线改进前后对比

图8 正弦修正加速度曲线改进前后跃度对比

以消除柔性冲击为目标，对正弦修正梯形加速度曲线进行改进，式(6)为其改进后的加速度曲线表达式。图7为改进前后加速度曲线对比，改进后的加速度曲线在运行的始末两端变化更加平缓。同时从图8两者的跃度曲线对比可以看出：改进后的跃度曲线消除了运行始末两端的突变，整个运行周期内跃度曲线均平滑过渡，消除了系统的柔性冲击。

4 结束语

本文在Delta机器人门形运动轨迹基础上，采用修正梯形加速度曲线对竖直-水平-竖直三部分运动进行轨迹规划和路径合成。在固定门形轨迹参数和运行周期的前提下，对竖直运动距离、竖直运动时间、水平运动时间三个参数进行寻优选择，得到了使Delta机器人主动臂电机轴端加速度最小的一组最优参数。同时为消除Delta机器人运动始末端的柔性冲击，提出了改进型的正弦修正梯形加速度曲线，保证了跃度曲线的连续。

[1] 丛爽，尚伟伟. 并联机器人：建模，控制优化与应用[M].北京：电子工业出版社，2010.

[2] 冯李航，张为公，龚宗洋，等. Delta 系列并联机器人研究进展与现状[J]. 机器人，2014，36(3)：375-384.

[3] LIU S，CHETWYND D G，HUANG T，et al. Optimal design of a 4-DOF SCARA type parallel robot using dynamic performance indices and angular constraints [J]. Journal of Mechanisms and Robotics，2012，4(3)：031005.

[4] 解则晓，商大伟，任凭. 基于 Lamé 曲线的 Delta 并联机器人拾放操作轨迹的优化与试验验证[J]. 机械工程学报，2015，51(1)：52-59.

[5] 颜雪松，胡成玉，姚宏，等. 精英粒子群优化算法及其在机器人路径规划中的应用[J]. 光学精密工程，2013，21(12)：3160-3167.

[6] 黄海忠. DELTA 并联机器人结构参数优化与运动控制研究[D]. 哈尔滨：哈尔滨工业大学，2013.

[7] M A LARIBI，L ROMDHANE，S ZEGHLOUL. Analysis and dimensional synthesis of the DELTA robot for a prescribed workspace [J]. Mechanism and Machine Theory，2007，(42)：859-870.

Delta Parallel Robot Pick and Place Trajectory Optimization

Li Yunhui

(Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun Jilin 130033, China)

On the basis of Delta parallel robot trajectory of gate-shaped picking and placing, we described the method of trajectory planning and gate-shaped path synthesis by using the sinusoidal correcting keystone acceleration curve. From the perspective of mechanical vibration and shock reduction mechanism, taking the initiative to reduce Delta robot arm maximum angular shaft as the goal, the relevant operating parameters of trajectory were optimized. For the presence of jerk mutations on the acceleration curve approach to planning the start and end-side movement, resulting in a flexible shock problem, it is proposed that modified sinusoidal correcting keystone acceleration curve, making the entire operating cycle jerk curve become continuous, eliminating the system flexible impact.

Delta robot; trajectory planning; path synthesis; parameter optimization; flexible impact

10.3969/j.issn.1000-3886.2016.03.007

TP242

A

1000-3886(2016)03-0020-03

李云辉(1989-)，男，黑龙江哈尔滨人，工学硕士，研究实习员，主要从事电气伺服系统控制方面研究。

定稿日期: 2016-01-18