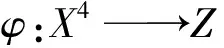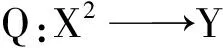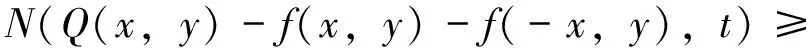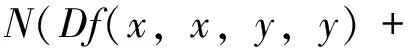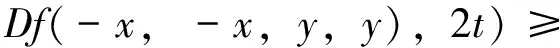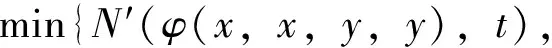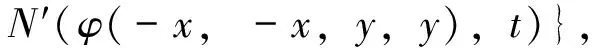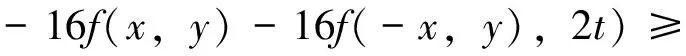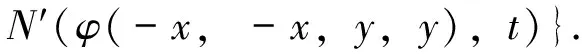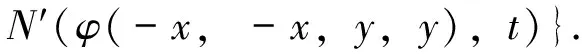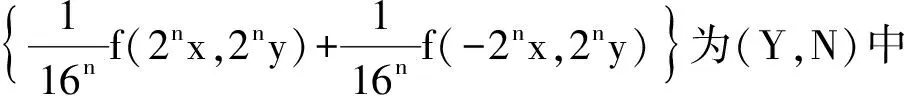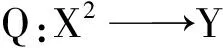Drygas二次型函数方程的Ulam稳定性
2016-12-06宋爱民
宋爱民
(甘肃民族师范学院数学系,甘肃合作 747000)
Drygas二次型函数方程的Ulam稳定性
宋爱民
(甘肃民族师范学院数学系,甘肃合作 747000)
给出了Drygas二次型函数方程的定义,并得到其一般解;讨论了Drygas二次型函数方程与混合三次-四次型函数方程的关系,并在Banach空间及模糊赋范空间上讨论了它的Ulam稳定性.
Drygas二次型函数方程;Banach空间;模糊赋范空间;Ulam稳定性
0 引言
1940年,Ulam[1]提出了函数方程的稳定性问题,并研究了群同态的稳定性,随后Hyers[2]解决了Banach空间中近似Cauchy映射的稳定性问题.1978年,Rassias[3]将这种稳定性推广到广义Ulam稳定性,此后人们研究了各种映射的Ulam稳定性[4-6].2003年,Radu[7]用不动点方法解决了Hyers-Ulam 稳定性问题,之后直接方法和不动点方法成为研究函数方程稳定性的重要方法.
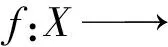

(1)

(2)
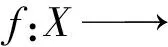

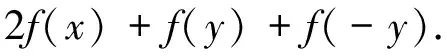
(3)
Drygas函数方程是Drygas[9]于1987年为了描述拟内积空间而引入的函数方程,对于一些统计学问题的解决起过重要作用.1992年,Ebanks等[10]给出了Drygas函数方程的一般解.
证明 必要性见文献[10].


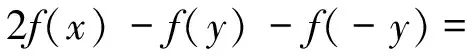
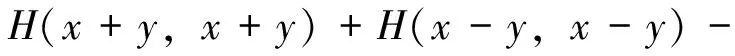


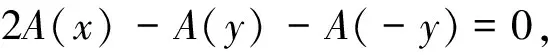
从而充分性得证.
事实上,这里
2008年,Gordji等[11]给出了混合三次-四次型函数方程

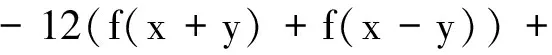
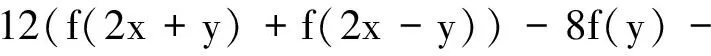

(4)
在Banach空间的稳定性并得到了其一般解.
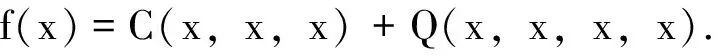

近几年,多元函数方程的稳定性引起了学者的广泛关注,如Chu等[12]研究了n元导子的每一个变量的Ulam稳定性,Bae等[13]研究了二元四次型函数方程的一般解及其稳定性.本文在上述研究的基础上,定义了Drygas二次型函数方程,并得到了它的一般解及其与混合三次-四次型函数方程的关系,最后讨论了其在Banach空间以及模糊赋范空间上的Ulam稳定性.
(5)
1 Drygas二次型函数方程的一般解
证明 充分性显然,下证必要性.
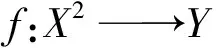
显然,f关于第一个变元是Drygas的,固定y1,y2,由引理2关于A的定义可知B关于第一个变量是可加的,又由引理2关于H的定义可知,F关于前两个变量对称可加;由于f关于第二个变元是二次的,由引理1及引理2中H的定义可知固定x1,则B关于后两个变量是对称、二次的;固定x1,x2,则F关于后两个变量是对称二次的.所以
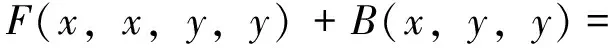
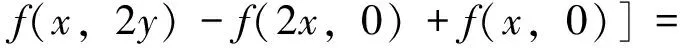
由于f关于第一个变元是Drygas的,从而f(2x,2y)-2f(x,2y)=f(x,2y)+f(-x,2y),也即
又f关于第二个变元是二次的,所以F(x,x,y,y)+B(x,y,y)=f(x,y),必要性得证.
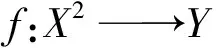



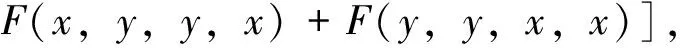
显然C关于三个变量是对称可加的,Q关于四个变量是对称可加的.不难看出,C(x,x,x)=B(x,x,x),Q(x,x,x,x)=F(x,x,x,x),从而

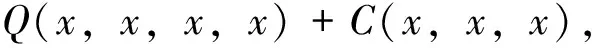
显然g满足引理3的条件,从而g为混合三次-四次函数. 】


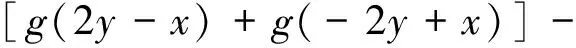
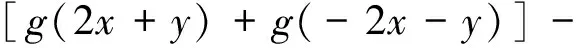
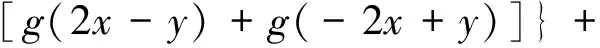
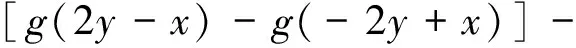
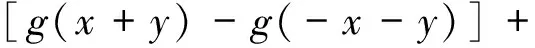
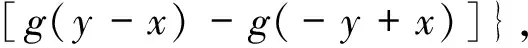
则f为Drygas二次函数,且g(x)=f(x,x).

Q(2y+x,2y+x,2y+x,2y+x)+
Q(2y-x,2y-x,2y-x,2y-x)=
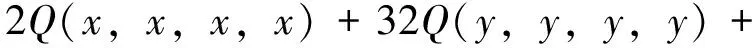
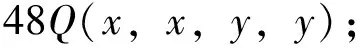
显然有
Q(2x+y,2x+y,2x+y,2x+y)+
Q(2x-y,2x-y,2x-y,2x-y)=
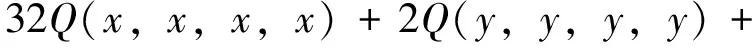
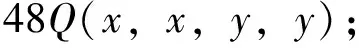
又
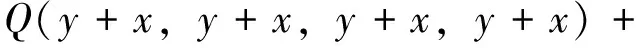
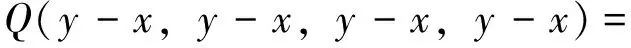

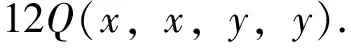
综合上面三式我们有
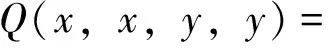
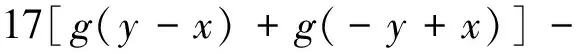
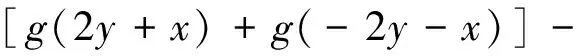
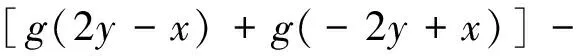

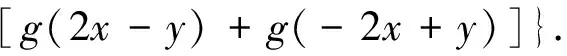
又因为

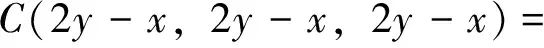
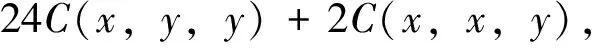
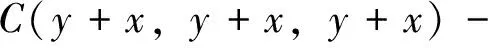

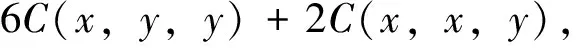
综合上面两式有


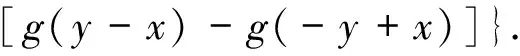
从而

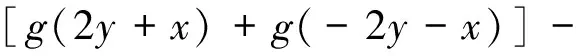


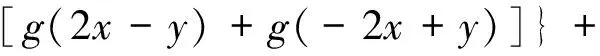


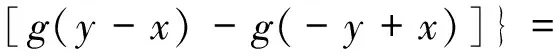
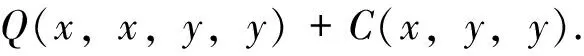
由定理1可知,f为Drygas二次的,显然有g(x)=f(x,x),定理得证. 】

显然f是Drygas二次的当且仅当对∀x1,x2,y1,y2∈X,有Df(x1,x2,y1,y2)=0.
2 Drygas二次函数方程在Banach空间上的Ulam稳定性
设X是实向量空间,Y是Banach空间.
(6)
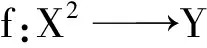
(7)
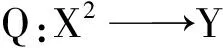
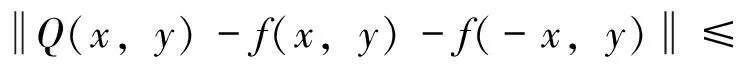
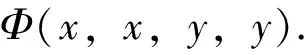
(8)
证明 由(7)式可知
(9)
在(9)式中令x1=x2=x,y1=y2=y,则有
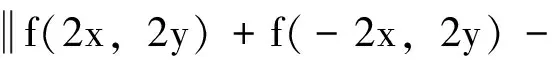
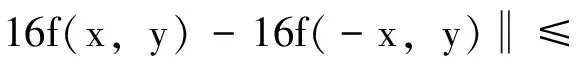
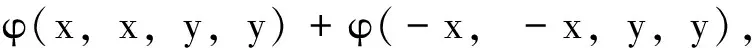
在上式中用2nx代替x,2ny代替y,且两边同除以16n+1,则有
(10)
从而对任意正整数m 由(6)式可知,序列 在(7)式中用2nxi代替xi,用2nyi代替yi,这里i=1,2,则有 设X为线性空间,(Y,N)是模糊Banach空间. φ(2x1,2x2,2y1,2y2)=αφ(x1,x2,y1,y2); (11) (12) (13) 其中M((x,y),t)=min{N′(φ(x,x,y,y),t),N′(φ(-x,-x,y,y),t)}. 证明 不失一般性,此处设0<α<16.由(12)式,显然有 (14) 在(14)式中令x1=x2=x,y1=y2=y,则有 也即 N(f(2x,2y)+f(-2x,2y)- 在上式中,用2nx代替x,2ny代替y,我们有 进一步,我们有 所以对任意正整数m 从而有 (15) 在(14)式中用2nxi代替xi,用2nyi代替yi,这里i=1,2,则有 从而 显然由上式有 从而 即Q为Drygas二次的. 在(15)式中令m=0,n→∞可得 从而定理得证. 】 [1] ULAM S M.ProbleminModernMathematics[M].New York:John Wiey & Sons,1940. [2] HYERS D H.On the stability of the linear functional equation [J].ProcAmerMathSoc,1941,72(2):222. [3] RASSIAS T M.On the stability of the linear mapping in Banach spaces [J].ProcAmerMathSoc,1978,72(2):297. [4] ESKANDANI G Z,GAVRUTA P,RASSIAS J M,et al.Generalized Hyers-Ulam stability for a general mixed functional equation in quasi-β-normed spaces[J].MediterraneanJournalofMathematics,2011,8(3):331. [5] NAJATI A,RANJBARI A.Stability of homomorphisms for a 3D Cauchy-Jensen type functional equation onC*-ternary algebras[J].JournalofMathematicalAnalysisandApplications,2008,341(1):62. [6] POPA D.Hyers-Ulam-Rassias stability of a linear recurrence[J].JournalofMathematicalAnalysisandApplications,2005,309(2):591. [7] RADU V.The fixed point alternative and the stability of functional equations[J].FixedPointTheory,2003,4(1):91. [8] JUNG S M.Hyers-Ulam-Rassias stability of functional equations in mathematical analysis[J].SpringerOptimizationandItsApplications,2001:175. [9] DRYGAS H.Quasi-innerProductsandTheirApplications[M].Advances in Multivariate Statistical Analysis,Netherlands:Springer,1987:13. [10] EBANS B R,KANNAPPAN P L,SAHOO P K.A common generalization of functional equations characterizing normed and quasi-inner-product spaces[J].CanadMathBull,1992,35:321. [11] GORDJI M E,EBADIAN A,ZOLFAGHARI S.Stability of a functional equation deriving from cubic and quartic functions [J].AbstractandAppliedAnalysis,2008(1):1563. [12] CHU H Y,KU S H,PARK J S.Partial stabilities and partial derivations ofn-variable functions[J].NonlinearAnalysis:Theory,Methods&Applications,2010,72(3):1531. [13] PARK W G,BAE J H.On a bi-quadratic functional equation and its stability[J].NonlinearAnalysis:Theory,Methods&Applications,2005,62(4):643. (责任编辑 马宇鸿) The Ulam stability of Drygas-quadratic functional equation SONG Ai-min (College of Mathematics,Gansu Normal University for Nationalities,Hezuo 747000,Gansu,China) A class of Drygas-quadratic functional equation is defined,and its general solution is obtained.Meanwhile,the relationship between Drygas-quadratic functional equation and cubic-quartic functional equation is given.Finally the Ulam stability of Drygas-quadratic functional equation in Banach space and fuzzy normed space is discussed. Drygas-quadratic functional equation;Banach space;fuzzy normed space;Ulam stability 10.16783/j.cnki.nwnuz.2016.06.005 2015-09-21;修改稿收到日期:2015-10-17 甘肃省高等学校科研资助项目(2015B-120) 宋爱民(1984—),男,甘肃兰州人,讲师,硕士.主要研究方向为算子代数及其应用. E-mail:songai-min@163.com O 177.1 A 1001-988Ⅹ(2016)06-0022-07
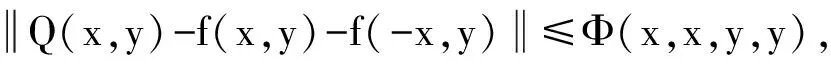
3 Drygas二次函数方程在模糊赋范空间的Ulam稳定性