高阶非线性薄膜方程的李对称分析
2016-12-06屈改珠
屈改珠
(渭南师范学院数理学院,陕西渭南 714000)
高阶非线性薄膜方程的李对称分析
屈改珠
(渭南师范学院数理学院,陕西渭南 714000)
利用李群分析方法研究了高阶非线性薄膜方程.首先,利用无穷小生成元方法得到了该方程的李代数及其最优系统,然后对方程进行约化,最后获得了一些具有特定物理意义的相似解.
高阶非线性薄膜方程;李对称分析;不变解
0 引言
对称群方法[1-7]是约化并求解非线性偏微分方程的有效方法之一,它是由挪威数学家Sophus Lie于19世纪末提出的,称作经典李对称群方法.该方法已广泛应用在数学、物理、工程以及非线性科学等相关领域,并产生了深远的影响.李对称群方法不仅可以研究方程的群理论性质,还可以得到与方程的完全可积性相关的某些数学特征.
本文利用李对称群方法研究2m阶非线性薄膜方程
(1)
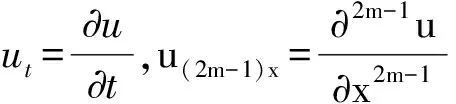
1 方程(1)的李对称和优化系统
1.1 方程(1)的李对称分析
下面利用李对称群方法研究2m阶非线性薄膜方程(1).假定方程(1)的解集在单参数李群变换
(2)
下是不变的,且
(3)
这里Dt,Dx分别表示关于t和x的全导数算子,即
上述变换群的无穷小生成元为
(4)
(5)
将(3)式代入(5)式,同时结合方程(1)消去ut,根据u的不同阶导函数的系数函数为零经计算整理可得关于未知函数ξ,τ,η的超定系统:
(6)


考察以下三种情形.
(A)f(u)为任意函数.解方程组(6)可得
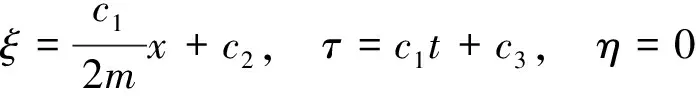
相应的3维李代数为:
(7)
(B)f(u)=up.解方程组(6)可得
相应的4维李代数为:
(8)
(C)f(u)=eau(a≠0).解方程组(6)可得
相应的4维李代数为:
(9)
1.2 方程(1)的优化系统
以下根据方程(1)允许的李对称及其交换关系,算出相应的伴随作用表示,进而利用群分析理论,给出方程(1)的优化子代数.
(A)f(u)为任意函数.方程(1)的3维子代数由V1,V2和V3构成,并有交换关系
将上面的李代数运算结果代入到伴随作用公式
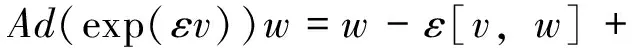
中,得到生成元(7)对应的伴随作用为

AdV1V2V3V1V1V2V3-12mεV1V2V1V2V3-εV2V3e12mεV1eεV2V3
设V=a1V1+a2V2+a3V3,为了进一步简化该向量,考虑下面几种情形:
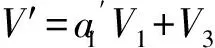
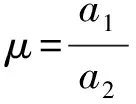
综上所述,当f(u)为任意函数时,方程(1)的最优系统为V1,V3,V2+μV1.
(B)f(u)=up.方程(1)的4维子代数由V1,V2,V3,V4构成,并有交换关系
其对应的伴随作用表示为
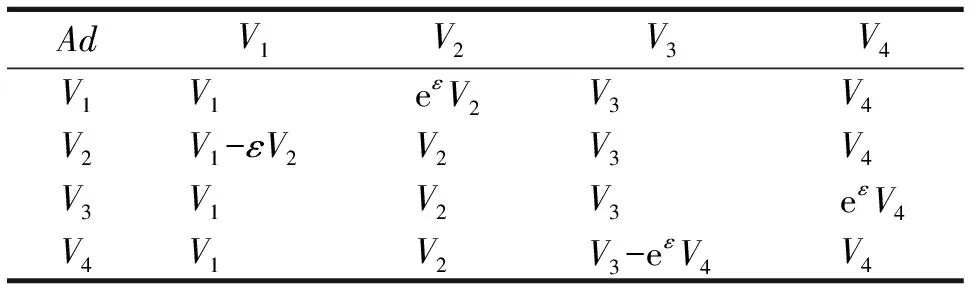
AdV1V2V3V4V1V1eεV2V3V4V2V1-εV2V2V3V4V3V1V2V3eεV4V4V1V2V3-eεV4V4
(C)f(u)=eau(a≠0).方程(1)的4维子代数由V1,V2,V3,V4构成,并有交换关系
其对应的伴随作用表示为
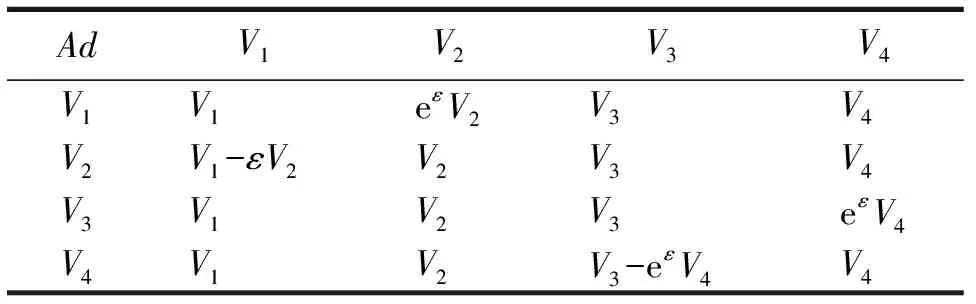
AdV1V2V3V4V1V1eεV2V3V4V2V1-εV2V2V3V4V3V1V2V3eεV4V4V1V2V3-eεV4V4
类似情形A计算方程(1)的最优系统的过程,我们得到其他两种情形的最优系统,结果见表1.
2 方程(1)的相似约化和不变解
2.1 方程(1)的相似约化
利用表1的最优系统我们得到方程(1)的三种情形对应的对称约化和群不变解,约化所得方程为常微分方程,分别由表2、表3、表4给出.

表1 方程(1)的优化系统

表2 f(u) 为任意函数时方程(1)的对称约化

表3 f(u)=up 时方程(1)的对称约化

表4 f(u)=eau 时方程(1)的对称约化
2.2 方程(1)的不变解
利用表1~4中的约化方程可以导出方程(1)的一些不变解,在此,我们仅就某些具有特定物理意义的相似解加以讨论[9,11].
(A)Source 解和sink 解.
因此,如果p>-2m,则当t→0时,u(x,t)→δ(x),且相似解为source解;如果p<-2m,则当t→+∞时,u(x,t)→δ(x),且相似解为sink解.同时对相应的常微分方程关于z积分一次,得到(2m-1)阶常微分方程
(10)
所以当f(u)=up时,高阶薄膜方程(1)被约化为(2m-1)阶常微分方程(10),且具有source解和sink解.
对表3中的情形5,我们取p=-2m,则相似解具有如下形式
因此,如果μ>0,则当t→-∞时,u(x,t)→δ(x),且相似解为source解;如果μ<0,则当t→+∞时,u(x,t)→δ(x),且相似解sink解.对相应的常微分方程关于z积分一次,得到(2m-1)阶常微分方程
(11)
所以当f(u)=up时,高阶薄膜方程(1)被约化为(2m-1)阶常微分方程(11),且具有source解和sink解.
(B)Waiting-time解.
表3中的情形1为一阶常微分方程,求解后得到高阶薄膜方程(1)具有waiting-time解
其中t0为任意常数.
(C)Blow-up解.
表4中的情形1为一阶常微分方程,求解后,得到高阶薄膜方程(1)具有解
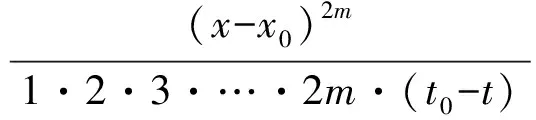
3 结论
本文利用李群分析方法讨论了2m阶薄膜方程(1),得到了该方程的李对称、最优系统、相似约化以及群不变解,进一步分析了方程的一些具有特定物理意义的相似解.对方程(1)的其他对称约化求解方面的研究,如非古典对称、势对称、非局域对称、势守恒律等,应是很有意义的后续工作.
[1]LIES.Überdieintegrationdurchbestimmteintegralevoneinerklasselinearerpartiellerdifferentialgleichungen[J].Arch Math,1881(6):328.[2] OLVER P J.ApplicationsofLieGroupstoDifferentialEquations[M].2nd ed.New York:Springer,1993.
[3] BLUMAN G W,KUMEI S.SymmetriesandDifferentialEquations[M].New York:Springer,1989.
[4] IBRAGIMOV H N.TransformationGroupsAppliedtoMathematicalPhysics[M].Boston:Reidel,1985.
[5] BLUMAN G W,ANCO S C.SymmetriesandIntegrationMethodsforDifferentialEquations[M].New York:Springer,2002.
[6] OVSIANNIKOV L V.GroupAnalysisofDifferentialEquations[M].New York:Academic,1982.
[7] GANDARIAS M L,BRUZN M S.Symmetry analysis and solutions for a family of Cahn-Hilliard equations[J].ReportsonMathematicPhysics,2000,46(1):89.
[8] ARONSON D G.The porous medium equation[C]//NonlinearDiffusionProblems.Lecture Notes in Mathematics,New York:Springer,1986,1224:1.
[9] GANDARIAS M L,MEDINA E.Analysis of a lubrication model through symmetry reductions[J].EurophysLett,2001,55(2):143.
[10] KING J R.The isolation oxidation of silicon:The reaction-controlled case[J].SIAMJApplMath,1989,49:1064.
[11] HUANG D J,YANG Q M,ZHOU S G.Group properties and invariant solutions of a sixth-order thin film equation in viscous fluid[J].JMathPhys,2013,54(1):013510(1-12).
(责任编辑 马宇鸿)
Lie symmetry analysis of a higher-order thin film equation
QU Gai-zhu
(School of Mathematics and Physics,Weinan Normal University,Weinan 714000,Shaanxi,China)
In this paper,Lie symmetry analysis approach is developed to study a higher-order nonlinear thin film equation.Using the infinitesimal generators,the Lie algebras and its optimal systems of the higher-order thin film equation are derived.The equation is then reduced to the ordinary differential equations.As a result,some physical interest solutions are obtained and discussed.
higher-order nonlinear thin film equation;Lie symmetry analysis;invariant solution
10.16783/j.cnki.nwnuz.2016.06.004
2016-04-08;修改稿收到日期:2016-06-22
国家自然科学基金资助项目(11371293,11501419);陕西省军民融合项目(15JMR20);渭南师范学院理工类科研项目(16ZRRC05);渭南师范学院校级特色学科建设项目(14TSXK02)
屈改珠(1978—),女,陕西蒲城人,讲师,博士.主要研究方向为偏微分方程.E-mail:qugaizhu.hi@163.com
O 175.2
A
1001-988Ⅹ(2016)06-0018-04
