多方法融合的粒子滤波算法的神经丝自动跟踪

巨 刚,袁 亮,刘小月

(新疆大学机械工程学院,新疆乌鲁木齐 830047)

多方法融合的粒子滤波算法的神经丝自动跟踪

巨 刚,袁 亮,刘小月

(新疆大学机械工程学院,新疆乌鲁木齐 830047)

神经丝蛋白质是医学中研究肌萎缩侧索硬化症病情进展的标志物.为了能精确捕获某种神经丝蛋白质在神经鞘中的活动特性,引入了一种多方法融合的粒子滤波算法跟踪神经丝蛋白质的运动.该算法汲取颜色直方图法、核函数法及图模法等的优点,融合粒子滤波算法,实现自动跟踪神经丝蛋白质.此外,为了解决粒子滤波中样本贫化,即在粒子滤波计算中很大一部分粒子重叠到一个单独的点上的情况,需要重采样计算解决此问题.但在重采样过程中,容易造成一些粒子丢失各向异性而导致跟踪精度降低,甚至跟踪目标失败,故结合粒子滤波算法提出了一种改进重采样约束方法.实验结果表明,基于改进重采样法及多方法融合的粒子滤波算法较传统算法能有效地减少样本贫化问题,并且可以高精度地跟踪移动、变形的神经丝蛋白质,为医学中神经丝蛋白质研究提供了新支撑方法.

目标跟踪;重要性采样;多方法融合;神经丝蛋白质;粒子滤波;重采样约束

神经丝蛋白质是研究轴突再生和神经退行性疾病的重要标志物质[1-2],提取神经丝蛋白质的活动特性成为研究神经丝蛋白质的重要环节.图1所示是通过荧光显微镜下实时地录制的某神经丝轴突中神经丝蛋白质单个和多个神经丝随机运动影像,图像中的神经丝蛋白质都是从左向右移动的.神经丝蛋白质都在神经轴突上移动,其测量半径约为5 nm,长度为几微米至十几微米不等.由于它们运动是间歇型的多向移动,无固定速率,无固定方向,随时都有可能伸长、缩短、突变多个、出现交叉等[3],因此具有很大的随机性.传统的做法是通过荧光显微镜录制到某神经丝蛋白质的运动视频,再通过人工标定的办法去跟踪,捕获神经丝蛋白质的运动特性,这将增长医学研究周期,还会带来人为性误差,给实验研究结果造成很大的干扰性影响.因此,研究神经丝蛋白质的运动特性,建立一种自动追踪目标的方法是十分必要的,这样就可以在提高跟踪效率的同时,制止人工操作的误差,在跟踪精度上消除人为因素的影响.

图1　单、双神经丝蛋白质在某神经元轴突中的运动情况(帧01,07,10,18,22,26,34,37,42)

目前,自动跟踪的算法有很多种类,比如卡尔曼滤波、扩展卡尔曼滤波、标准粒子滤波算法等.图像跟踪技术被广泛地应用到各个重要领域中,例如无人机跟踪、视频监控跟踪、微生物医学工程领域.文献[4]采用轴突分解成块,利用马尔可夫随机场图形标签来确定神经丝运动情况;文献[3]利用粒子滤波新算法跟踪神经丝蛋白质,限制粒子的位置和方向提高了跟踪精度,降低粒子数量减少了运行时间,提高跟踪效率;文献[5]采用图像分割技术结合粒子滤波对微管细胞进行跟踪,利用图像每帧之间的信息,对细胞主轮廓进行识别,捕获跟踪信息;文献[6]在标准粒子滤波中融合均值偏移(Mean Shift)算法,筛选出权重较大的粒子,舍弃权重接近为零的粒子,解决了粒子衰减问题,并且降低了计算耗时量;文献[7]详细介绍了传统粒子滤波(Particle Filter,PF)、扩展卡尔曼滤波(Extended Kalman Filter,EKF)、近似基于网格的(Grid-Based)方法及其他相关粒子滤波算法,对复杂目标跟踪提供选择依据;文献[8]在标准粒子滤波预测过程中,每一步粒子更新采用光滑状态估计法,使得基于建议分布粒子滤波算法更精确.

鉴于此,笔者对神经丝蛋白质进行自动跟踪,采用图像颜色直方图法、核函数法及图模法综合融入粒子滤波算法,在标准粒子滤波基础上对重采样过程进行区域约束,使得粒子在重采样过程中不再丧失粒子各向异性.同时与传统粒子滤波算法相比较,使得跟踪精度更高,跟踪目标过程中更可靠,更有效率.

1　粒子滤波算法

粒子滤波是基于一种蒙特卡洛的近似贝叶斯滤波算法,采用数理统计思想即用一些离散型随机粒子来近似系统分布的概率密度函数,常用在非线性和非高斯的系统环境中,对神经丝蛋白质的鲁棒性实时跟踪具有很高的效率与可靠性.

神经丝蛋白质跟踪的状态矢量是由运动学参数和椭圆特征参数组成的,笔者采用的状态矢量为

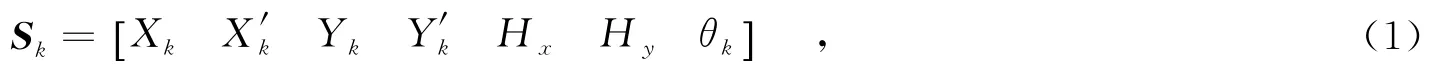
其中,(Xk,Yk)是椭圆中心位置;(X′k,Y′k)是椭圆跟踪速度;Hx,Hy分别是椭圆的短半轴、长半轴;θk为方向角(x轴和椭圆短半轴的夹角).

神经丝样本是通过运动状态模型方程逐步更新粒子的,更新方程为

其中,H为转移矩阵;N(·)为多元参数的高斯随机变量,Rk是分别和σ_Hx,σ_Hy,σ_θk协方差相关的矩阵.在神经丝蛋白质跟踪的应用中,H随着X′k,Y′k,θ变化而转移,在两帧之间认为X′k,Y′k是恒定的.

标准粒子滤波程序如下[6,9]:

在时间t=0时,

步骤1 初始化.For j=1,…,N,从先验分布p(x0)采样xj0在时间t=1,2,…For j=1,…,N.

步骤2 预测.从St-1繁殖的每个样本都是通过线性随机的微分方程(2)实现的.

2　改进粒子滤波跟踪策略

2.1改进重采样方法

在重采样过程中,Neff为有效粒子数量,用它来估计衰减粒子数量.当Neff低于设置的阈值Ndegenercy时,就会进行重采样来弥补衰减粒子数量,在神经丝蛋白质跟踪实验中设置Ndegenercy为120.重采样过程可以减少有效粒子衰减现象,但是带来的却是丧失粒子各向异性,可能导致跟踪精度降低,甚至跟踪目标失败.因此,提出了一种新的重采样方法来解决这个问题.

根据贝叶斯理论,先验分布参数被作为统一的分布,但是它没有跟踪过程中的观测信息,可能导致跟踪不准确.在神经丝蛋白质跟踪实验中,笔者采用的是在临近区域内的新粒子被假设作为统一的分布,即采样粒子区间给予约束区域:

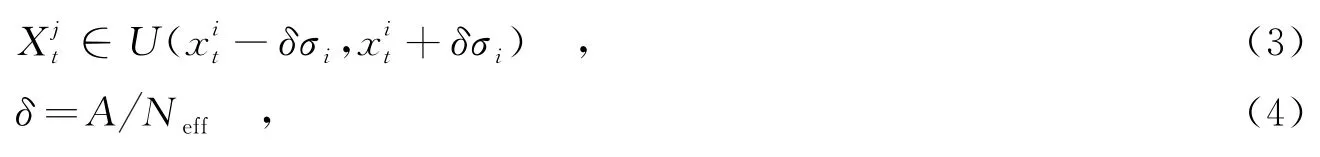
2.2改进粒子更新方法

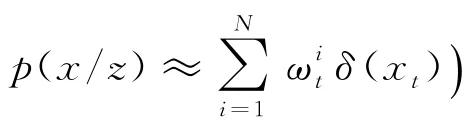
2.2.1后验概率估计目标跟踪策略

对目标进行同时跟踪,用变差法对图像模型近似推理,即引入一个以后验估计p(x/z)为变量的函数Q(x),通过对Q*(x)函数分布求解最优结果(p(x/z)为最优解)即使得Q(x)和变量之间的Kullabck-Leibler(KL)Divergence最小,表示关系如下:

为了能对Q*(x)进行理论近似求解,可以用拉格朗日方程对Q(x)进行约束,即

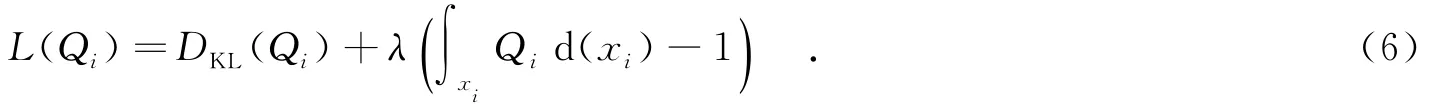
用高斯分布表示目标先验分布,在t时刻可以得到一个关于Q(x)函数的迭代方程,即

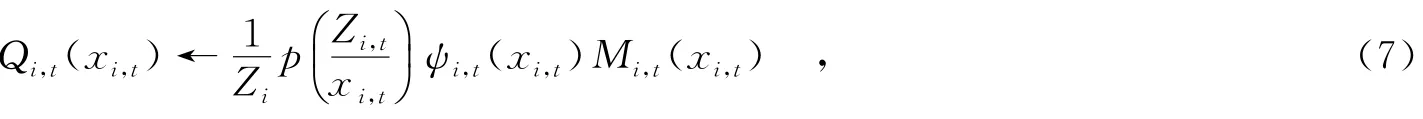
由于方程(7)收敛,Qi,t(xi,t)的不断更新,使得DKL逐渐减少余量,直至达到平衡,进而求得目标后验分布最优解p(x/z).

2.2.2似然函数目标跟踪策略

以色度-饱和度-纯度色彩模型(Hue-Saturation-Value,HSV)为基础对所需要甄别的神经丝目标进行直方图建模.设神经丝图像目标的颜色量化表为6×6×6等级,表示H、S、V的颜色通道等级分别是6级,图像颜色量化函数为

其中,x(lm)表示lm处的图像颜色值量化并分布到颜色直方图上的颜色响应等级,为了减少背景颜色的影响,采用权重直方图法.权重直方图是由图像颜色分布核函数决定,核函数[11-12]为

其中,zi=1,…,M,为中心领域到像素位置的距离;c为归一化权系数;k(·)为像素匹配权值,表示准确挖掘边缘像素的数据及增加获取颜色数据的可控性.远离目标像素的中心位置程度越大,权重越小.

候选目标颜色直方图是描述实际目标的近似函数,表示为

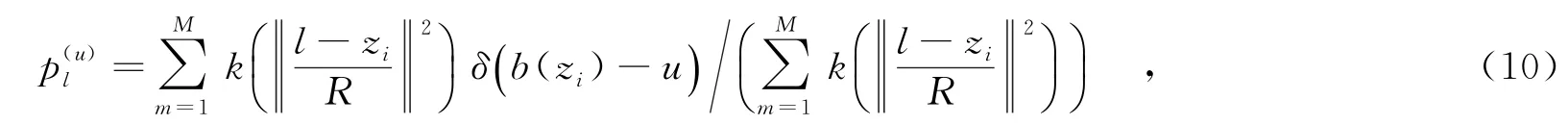
其中,M为像素总数;l为目标中心坐标(x,y);R为候选目标域半径;u为图像颜色量化等级,取值为1～X; b(zi)是在像素zi位置处的直方图;δ(·)为Kronecker Delta函数.

图像目标初始帧为选择的参考模X0,用式(7)建立参考目标核函数直方图为实际目标X的核函数颜色直方图.设X和X0之间为相似度似然关系.选择Bhattacharrya为似然函数相似度,定义为

其中,ρ∈[0,1],称为巴氏系数,也称为甄别度.ρ=0,表示无相似程度,甄别度为零;ρ=1,表示参考值和目标值完全相同,甄别度为1.实验中定义两种分布之间距离为

其中,D(p,q)称为Bhattacharrya距离.

在神经丝蛋白质跟踪中,采用高斯密度函数作为颜色直方图的候选目标和参考目标分布的似然函数,即

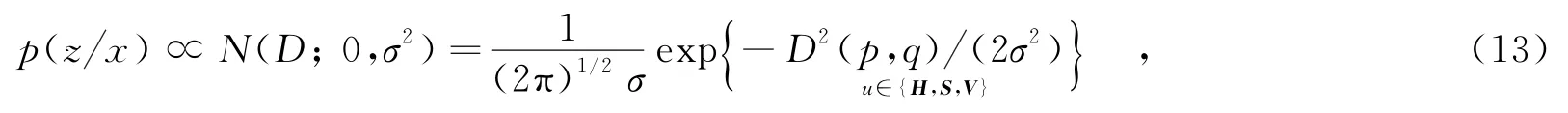
其中,σ为颜色高斯方差.甄别度越小,实际采样目标越准确,目标观测概率数值越大.

多方法融合粒子滤波算法如下:

(1)将2.2.1节求解的p(x/z)带入到步骤3后,后验概率估计p(x/z)同时将式(3)～(4)采样约束条件带入步骤4,可以得到改进粒子滤波算法求解结果.

(2)将式(13)代入到步骤3,更新似然函数p(z/x),再计算后验概率估计p(x/z),同时将式(3)～(4)采样约束条件带入步骤4,可以得到改进粒子滤波算法求解结果.

以上两种途径都可以求解到结果,笔者采用的是(1)和(2)混合使用,最终求解加权均值.

3　实验结果分析

神经丝蛋白质跟踪实验所用图像是在荧光显微镜下录制的真实视频.跟踪方法包括改进粒子滤波算法和标准粒子滤波算法.在神经丝蛋白质跟踪中进行了两组实验,第1组是单神经丝蛋白质的跟踪,第2组是双神经丝蛋白质目标跟踪.单目标跟踪实验中选取帧(07,10,15,20,25,30,40,43,45)为研究对象,双目标跟踪实验中选取帧(00,04,11,20,25,30,40,47,49)为研究对象.

图2是神经丝蛋白质单目标跟踪结果.左边设置纯色单个目标理想场景目标的特征凸显.右边人为地设置了标准偏差的白噪音,其信噪比为1.7.跟踪视频结果显示,标准粒子滤波跟踪过程在第25、30、40帧时丢失目标,而改进粒子滤波在添加白噪音的整个跟踪过程中都能准确地捕获无规则移动的神经丝蛋白质,并准确跟踪其位置,具有很高的效率与可靠性.

图2　标准粒子滤波及改进粒子滤波算法的单个神经丝跟踪结果(右信噪比为1.7)

图3　标准粒子滤波及改进粒子滤波算法的双神经丝跟踪结果(右信噪比为1.7)

图3是双神经丝蛋白质上目标跟踪结果,同样右边人为地设置了标准偏差的白噪音,其信噪比为1.7.两个椭圆分别跟踪长神经丝蛋白质和稍短神经丝蛋白质,神经丝在移动过程中是随机无规则运动的,在某瞬时还可能发生缩短、变长等复杂变形现象,都可能影响跟踪精度.如图3的长神经丝第11帧和第30帧发生缩短变形,当两个目标接近、交叉时出现丢失指定的跟踪目标等现象,左边第25、30、40帧丢失目标.双神经丝蛋白质跟踪结果表明,在这些复杂的环境下,改进粒子滤波算法能快速地、高精度地捕获目标,相比标准粒子滤波算法有很好的鲁棒性和可靠性.

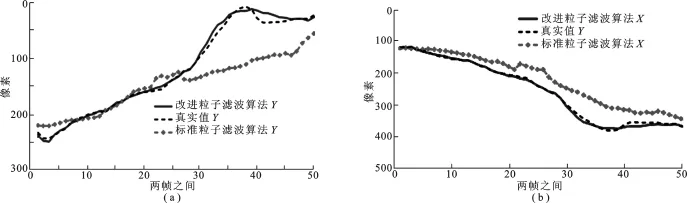
图4　粒子滤波的神经丝跟踪Y-X方向位移

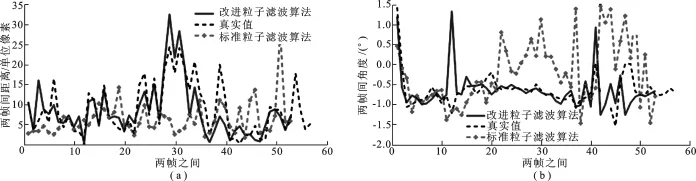
图5　粒子滤波的神经丝跟踪两帧之间距离及角度

图4～图7是单神经丝蛋白质跟踪实验的数值化分析.由于神经丝蛋白质跟踪过程存在随机性,因此图4～图6是在实验用200个粒子[3]条件下进行了80次重复试验.对计算的加权平均标准粒子滤波数值、加权平均改进粒子滤波数值及真实值分别在X/Y方向位移、X/Y方向速度、偏角及两帧间距离进行比较,结果显示了标准粒子滤波在每一帧中都有相当大的跟踪误差,而改进粒子滤波算法产生的神经丝蛋白质跟踪误差较小(分布在0.0%～7.5%),跟踪的位移、速度、偏角都很接近真实值.图7是改进重采样约束下的重采样粒子分布直方图,能明显看出采样粒子的分布较均匀,没有丧失各向异性,对能准确跟踪神经丝蛋白质目标起到决定性作用.这些结果充分表明,标准粒子滤波算法在复杂干扰中无法跟踪视频中的神经丝蛋白质目标,而改进粒子滤波算法能够准确地跟踪单、双目标,具有高的可靠性.

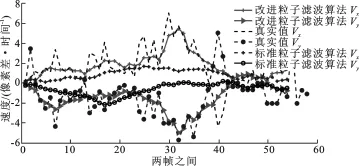
图6　粒子滤波的神经丝跟踪两帧之间速度

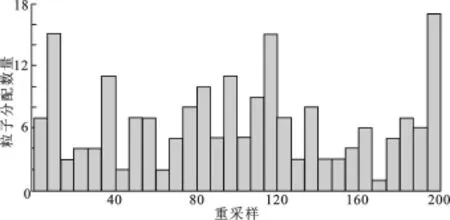
图7　改进粒子滤波重采样的粒子分配数量直方图

4　总 结

由于神经丝蛋白质的鲁棒性、非线性和不稳定性,使得对于神经丝蛋白质的实时追踪成为一项非常艰巨的任务.标准粒子滤波不能准确地跟踪到目标,并且在跟踪重采样过程中大量粒子丧失各向异性,最终导致跟踪目标失败.为了解决以上问题,笔者提出了一种多方法融合的粒子滤波算法,在高斯核函数及图模差分法基础上对各帧图像相似度进行对比,使得跟踪目标及时获得修正信息,保证粒子跟踪目标的准确性,并且在重采样过程中对需要采样粒子进行区域约束,确保粒子不会丧失各向异性.实验结果表明,改进粒子滤波算法对于神经丝蛋白质的单、双目标跟踪相比标准粒子滤波算法具有高精度和高可靠性.

[1]WANG H T,WU M F,ZHAN C J.Neurofilament Proteins in Axonal Regeneration and Neurodegenerative Diseases [J].NEU-RAL Regeneration Research,2012,7(8):620-626.

[2]ZHU J D,YUAN L.Neurofilament Tracking by Detection in Fluorescence Microscopy Images[C]//Proceedings of 2013 IEEE International Conference on Image Processing.Piscataway:IEEE,2013:3123-3127.

[3]YUAN L,Zheng Y F.Object Tracking With Particle Filtering in Fluorescence Microscopy Images:Application to the Motion of Neurfilaments in Axons[J].IEEE Transactions on Medical Imaging,2012,31(1):117-130.

[4]袁亮,朱俊达.基于检测的荧光显微镜图像中的神经丝蛋白跟踪[J].计算机工程与科学,2013,37(1):119-124. Yuan Liang,Zhu Junda.Neurofilaments Tracking by Detection In Fluorescence Microscopy Images[J].Computer Engineering&Science,2013,37(1):119-124.

[5]BAI K J,LIU W M.Improved Object Tracking with Particle Filter and Mean Shift[C]//Proceedings of the IEEE International Conference on Automation and Logistics.Piscataway:IEEE,2007:431-435.

[6]KONG K Y,MARCUS A I,GIANNAKAKOU P,et al.Using Particle Filter to Track and Model Microtubule Dynamics[C]// Proceedings of the IEEE International Conference on Image Processing:5.Piscataway:IEEE,2007:517-520.

[7]ARULAMPALAM M S,MASKELL S,GORDON N,et al.A Tutorial on Particle Filters for Online Nonlinear/Non-Gaussion Bayesian Tracking[J].IEEE Transactions on Signal Processing,2002,50(2):174-188.

[8]JU B,ZHANG Z H,ZHU J B.A Novel Proposal Distribution for Particle Filler[C]//Proceedings of the 2010 3rd International Congress on Image and Signal Processing:7.Piscataway:IEEE,2010:3120-3124.

[9]SMAL I,GRIGORIEV I.Microtuble Dynamics Analysis Using Kymographs and Variable-Rate Particle Filters[J]. IEEE Transactions on Medical Imaging,2010,19(7):1861-1876.

[10]宋长贺,李云松,宁纪锋,等.分布场的多特征融合目标跟踪方法[J].西安电子科技大学学报,2015,42(4):1-7. SONG Changhe,LI Yunsong,NING Jifeng,et al.Study of Multi-feature Fusion Methods for Distribution Fields inObject Tracking[J].Journal of Xidian University,2015,42(4):1-7.

[11]崔丽珍,李蕾.基于核函数法及粒子滤波的煤矿井下定位算法研究[J].计算机工程与科学,2013,26(12):1729-1733. CUI Lizhen,LI Lei.Research on Underground Coal Mines Positioning Algorithms Based on Kernel Function and Particle Filter[J].Chinese Journal of Sensrsand Actuators,2013,26(12):1729-1733.

[12]袁广林,薛模根.基于核函数粒子滤波和多特征自适应融合的目标跟踪[J].计算机辅助设计与图形学学报,2009,21 (12):1774-1784. YUAN Guanglin,XUE Mogen.Kernel-Based Particle Filter for Target Tracking with Adaptive Multiple Features Fusion [J].Journal of Compter Aided Design&Computer Graphics,2009,21(12):1774-1784.

(编辑:郭 华)

Neurofilament protein automatic tracking of the particle filter algorithm based on multiple methods fusion

JU Gang,YUAN Liang,LIU Xiaoyue
(School of Mechanical Engineering,Xinjiang University,Urumqi 830047,China)

The neurofilament protein serves as the marker of the state for ALS(Amyotrophic Lateral Sclerosis)in the medical filed.In order to accurately capture the motion characteristics of the neurofilament protein in the axon,a new-type algorithm based on the particle filtering of multiple methods-fusion is introduced in this paper.This fusion algorithm integrates the advantages of the color histogram,kernel function method,and graph model strength into the particle filtering algorithm.In addition,in order to solve the problem of sample impoverishment,which will lead to the majority of particles overlapping on one single point in the computation of the particle filter,the re-sampling method is utilitied.However,the resampling method easily causes the loss of the particle anisotropy,which will reduce the tracking precision or even fail to the track.We present a new re-sampling constrained method to improve the particle anisotropy in the particle filtering.Experimental results indicate that the algorithm based on the improved method of re-sampling and the particle filter of multiple methods-fusion can effectively reduce the number of overlapping particles and precisely track the deformed neurofilament protein.Such a tracking method will be helpful in the research on the neurofilament protein in the medical filed.

target tracking;importance sampling;multiple methods-fusion;neurofilament protein; particle filtering;re-sampling constraints

TP391

A

1001-2400(2016)04-0184-07

10.3969/j.issn.1001-2400.2016.04.032

2015-08-28

国家自然科学基金资助项目(31460248,61262059);新疆优秀青年科技创新人才培养资助项目(2013721016);新疆大学博士启动基金资助项目;自治区科技支疆资助项目(201591102);新疆自治区研究生科研创新资助项目(XJGRI2015025)

巨 刚(1988-),男,新疆大学硕士研究生,E-mail:jugedu@163.com.