测量报告数据的谱分析压缩算法

程 飞,刘 凯,丁文文,时 欢,张百戬

(西安电子科技大学计算机学院,陕西西安 710071)

测量报告数据的谱分析压缩算法

程 飞,刘 凯,丁文文,时 欢,张百戬

(西安电子科技大学计算机学院,陕西西安 710071)

针对网络带宽难以满足海量测量报告传输要求,定义了测量数据的谱,并提出了测量报告数据的谱分析压缩算法.该算法通过分析测量数据的谱,提出了对数据完成两次排序的预处理方案,减少了数据冗余的间隔距离,以期提高上下文的命中率.其次,该压缩算法构建了测量数据的多个上下文模型,并作为单层神经网络的输入结点.神经网络通过对每个上下文模型的预测概率线性组合,得到对下一比特的预测概率,并用真实的下一比特来调整对应输入结点的权重,提高匹配历史信息的概率.实验结果表明,在采用该压缩算法后,算法的运行时间明显减小,压缩率随被压缩数据量的增大而提高.与其他通用压缩算法相比,该算法能有效提高测量数据的压缩率,从而达到减少网络数据传输量的目的.

测量报告;数据压缩;谱分析;神经网络

移动运营商需要对正式投入运行的通信网络进行数据采集和分析工作[1],以洞悉通信状态的动态变化.其主要收集用户终端发出的测量报告(Measure Report,MR),获知所辖的移动网络状态.测量报告包含接入电平门限、切换电平门限、话务密度等性能参数,并且记录移动通信网络的配置.测量报告数据采集过程如图1所示,处在某蜂窝网中的用户终端随时会与基站保持通信,将测量报告通过基站和基站控制器传输并保存到数据采集服务器上.数据采集服务器周期性将数据远程传输到数据中心,以便于全面地了解网络的运行状况,及时地发现网络故障,并针对问题给出解决方案.随着终端用户增加,MR数据量出现大幅度的增长.数据采集服务器与数据中心之间的带宽有限,难以适应测量数据的海量传输.为减少数据传输量,需要对MR数据进行压缩处理.

现有的文本压缩算法主要是针对常规文本数据的压缩过程[2-7].如文献[2]使用字典编码的机制,用偏移加长度的方式表示重复出现的字符串,结合哈夫曼编码和Deflate来压缩文本数据.文献[3-4]提出基于上下文模型的预测的自适应性的统计数据压缩技术,该系列算法将不同阶的上下文模型混合预测输入序列的下个字符.文献[6]中的压缩算法思想与局部匹配预测(Prediction by Partial Matching,PPM)类似,与其不同的是,其利用多层神经网络将上下文模型混合,得到下个字符的预测概率.文献[7]提出用伯罗斯惠勒变换(Burrows-Wheeler Transform,BWT)将重复性的字符序列转换为同样字母组成的字符串,再利用前向移动技术和哈夫曼编码处理文本.

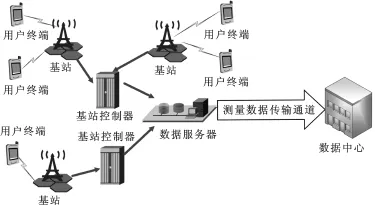
图1　测量报告数据采集示意图

与其他文本[8]和图像[9-11]压缩问题不同,测量数据是一种特殊的文本数据.测量数据中冗余信息的间隔距离对这些算法提出了挑战.距离间隔是冗余信息在原始数据的偏移量的差值,表现为冗余信息之间其他字段所占用的字节数.由于MR数据是由多个MR报文顺序组成的,冗余信息的间隔距离分为报文间距和字段间距两种情况,报文间距为数据冗余多的报文之间存在多个报文;相邻报文的同一字段之间存在其他字段,这些字段形成了字段间距.当冗余信息的间隔距离过长时,常规压缩算法无法在有限的上下文模型的范围内查找成功,信息的数据编码变长,导致数据压缩效果不明显.

笔者提出了一种基于谱分析的MR数据压缩算法,该算法定义了MR的谱,同时根据谱分析的结果对MR数据采取两次排序的预处理方案.该预处理过程分为多关键字归并排序与合并字段排序两个步骤.多关键字归并排序提出对MR联合TRXID和MXID字段联合排序,提高相邻报文的相似性,减少报文间距.在联合字段排序的基础上合并字段排序,减少字段间距.其次,压缩算法采用神经网络模型,笔者提出了建立适合MR数据的上下文模型,每个上下文模型均输出上下文预测概率,将这些概率预测混合得到下个字符的预测概率,并将混合的预测概率代入算术编码器进行字符编码.

1　MR 数据压缩算法

1.1MR谱分析

数据收集服务器收集每个终端的MR报文发送给数据分析中心.若终端在某时间段内的某些通信特征不发生明显变化,该段时间的MR数据在时间上存在冗余,则称为时间相关性.若某个蜂窝网中的终端数目可达到一定的密度,所监测的信号范围相互交叠,则称为空间相关性.时空相关性[12]是MR存在数据冗余的原因,然而由于各个基站通信状态和数据收集时间是相互独立的,MR报文到达数据收集服务器时间也是相互独立的,MR文件中的报文次序是随机排列的.因此,存在含有冗余信息的报文在MR文件存储顺序是非相邻的情况.为提高MR数据的压缩率,可结合MR数据时空相关性调整报文的顺序,减小冗余信息的间隔距离.MR报文包含若干字段,选取何种字段作为调整MR文件中报文次序的依据成为难题.假设从某个特定的时刻开始采集数据,直到另一个固定时刻为止,获得MR数据表示成矩阵形式为

其中,Xk=(xk1,xk2,…,xkm)T,(k∈N,N={1,2,…,n})是MR数据中第k个报文;xkj(k∈N,j={1,2,…,m})是第k个报文的第j字段,m为MR报文中字段总数.矩阵Y的每行表示1个报文,每个列表示某个数据字段.向量Xk与Xj的欧式距离Sk,j表示报文Xk与Xj的相似性,Sk,j的数值越小,报文Xk与Xj相似性越大,则报文之间存在冗余信息的概率越大.MR数据是以报文为单位顺序存储的,选取不同的字段排序后,相邻报文的相似性会发生改变.相邻的报文相似性越大,MR数据中冗余距离减小的可能性就越大.为此,笔者提出了MR数据的谱dY的定义.dY是指为所有相邻报文相似性的均值,可表示为

其中,Si,i+1表示第i个报文和第i+1个报文的相似性,谱的值越小,冗余数据的间隔距离就越小.矩阵Y按照m个字段分别排序后的谱均有变化,按第k个字段排序的MR谱记为dY(k).若能够找到min dY(k),就能够最大程度地减少数据冗余的距离.

以MR数据为实验对象.该数据由360 096个MR报文构成,按其所含59个不同字段分别调整报文顺序,计算得到的排序后的MR谱dY(k),如图2所示.图2中,横坐标表示MR报文的所有字段,纵坐标表示MR数据按某字段排序后的谱dY(k),水平虚线是表明为未进行字段排序的MR初始的谱dY(0),可作为排序后对比的基准.由图2可知,按MXID排序的谱最小,TRXID排序次之.因此,MXID排序后,相邻报文的冗余信息较大,或者说冗余信息的间隔距离较小.字段MXID表示基站号,字段TRXID表示载频号.在同一个基站的范围内的用户终端,MR数据中的基站号相同,具有空间相关性;一个基站内不同用户设备(User Equipment,UE)被分配的载频号不同,MXID和TRXID相同的报文表示同一UE的MR消息,具有时空相关性.以上按不同字段排序后的MR相关性的分析方法,称为谱分析.

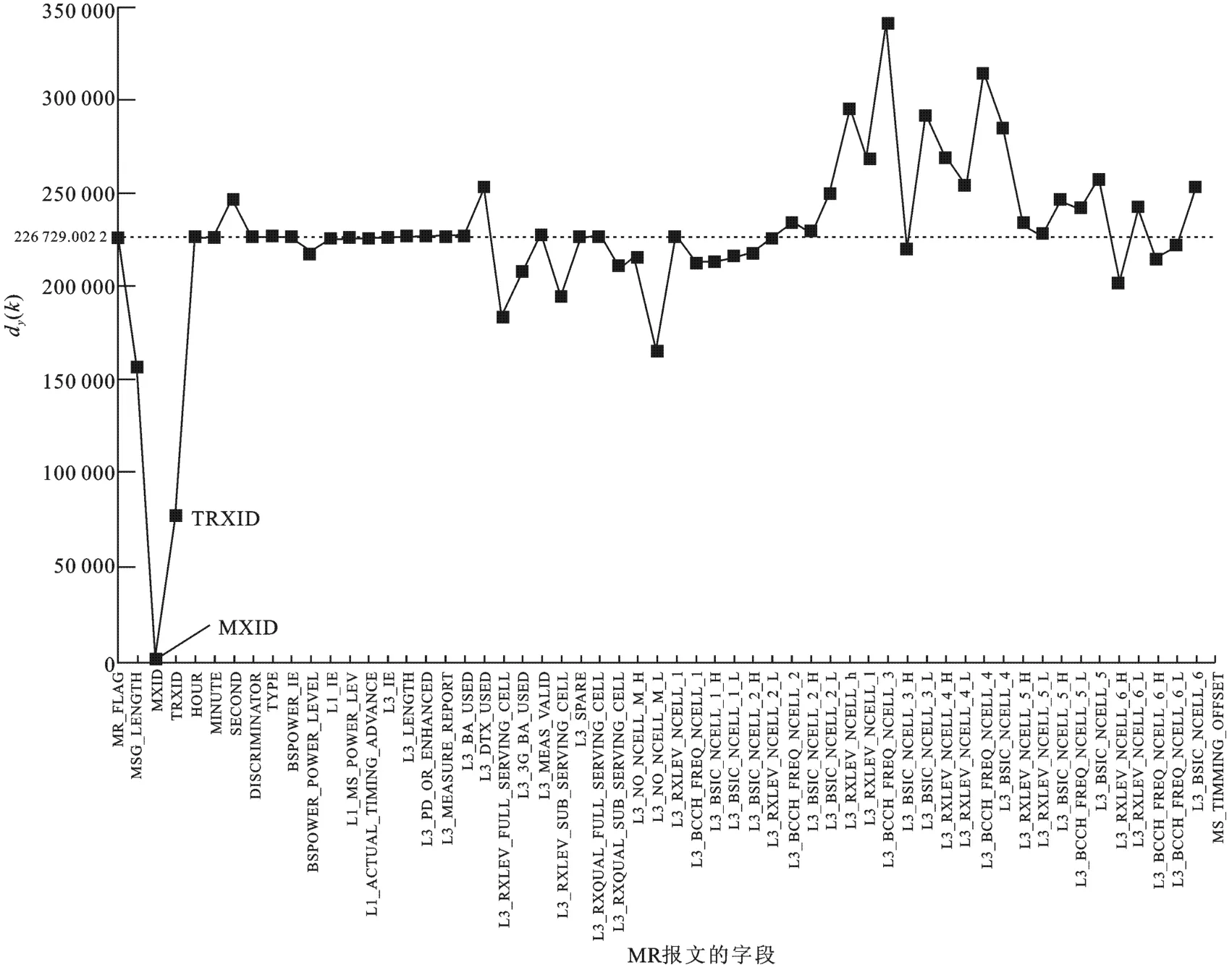
图2　MR数据的谱分析

1.2多归并排序

依据MR谱分析,可对MR报文按MXID和TRXID多归并排序.多communications Measure Report,GSM-MR)数据格式中,MXID和TRXID是相邻字段,MXID字段位数是4 B,TRXID字段位数是2 B.将MXID和TRXID映射到一个64 bit的无符号整型数据中,高16 bit用0填充.在多字段排序中,依据每个报文中MXID和TRXID对应的64位无符号整型为主键,将多

归并排序变为一次归并排序,最好情况和最坏情况的时间复杂度都为n log(n).从矩阵角度来看,多

归并排序就是根据列的数值重新排矩阵Y的行序列.

按照相关度大小选择排序多个字段,第1个排序主字段为MXID,第2个排序主字段为TRXID.首先,依据MXID的值对MR数据进行归并排序,改变数据的初始顺序;当MXID的数值相等时,依照TRXID再进行归并排序.一次归并排序的最好情况和最坏情况的时间复杂度均为n log n.多

分别排序是两次归并,时间消耗较大,时间复杂度是n log n≤T(n)≤2n log n.在全球移动通信系统测量报告(Global System for Mobile

1.3合并字段排序

多归并排序后,相同字段间还存在字段间距,这会影响概率预测准确度.多T,其中,归并处理文件对应的矩阵(Y′)T,即对n×m矩阵Y′按列排序生成m×n矩阵(Y′)T.

归并排序后的MR数据称为MR归并数据,记为Y′.将MR归并数据中所有报文的同字段依次顺序排列,减少字段间距.具体地说,将所有报文的第1个字段顺序排列,接着将第2个字段顺序排列,以此类推.对于矩阵将第1列代表的字段作为整体,接着把第2列代表的字段排在第1列的后面,即对矩阵Y′进行转置变换(Y′)

1.4基于神经网络的多上下文编码

将MR的各字段扩展为整字节的数据字段,笔者对此提出建立4类上下文模型,分别为半字节上下文模型、整字节上下文模型、双字节上下文模型以及四字节上下文模型.其中,每个上下文模型通过匹配输入比特得到的预测概率为Pi,i=1,2,…,4;4个上下文模型的预测概率Pi通过单层神经网络加权线性混合后得到的输出预测概率为P.输入Pi,神经网络的输入结点可表示为

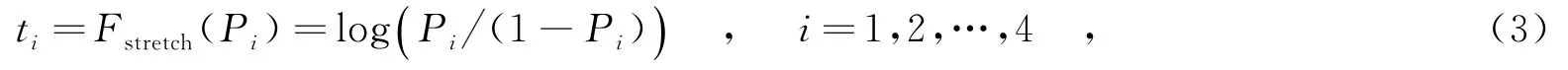
神经网络的预测概率P可表示为

其中,y是输入的下一比特;y-P是预测误差;γ为学习率,其取值不宜过大,取值为0.002.P作为算术编码器编码的依据,设字符s出现的概率为P(s),那么为该字符分配一个在Q和Q+P(s)之间的数作为编码,其中Q为所有在字符s之前出现的概率之和.基于神经网络的多上下文编码该过程被记为XDMRC(XDMR Coding).综合形成的MR压缩算法步骤如下:

(1)对输入的MR进行谱分析,按照TRXID和MXID进行多归并排序,减少报文间距.

(2)对归并排序后的MR进行合并字段排序,减少字段间距.

(3)4个上下文模型匹配已输入字段,输出每个模型的预测概率Pi,利用式(3)和式(4)得到神经网络的预测概率P,将P送入算术编码器编码.

(4)利用式(5)将读入的下一比特y来调整神经网络中每个输入结点的权重wi.

2　实验结果及分析

笔者采取3组实验来说明所提出的XDMR压缩算法的有效性.XDMR压缩算法采用C语言编写,实验测试环境的机器配置为3.0 GHz主频的Intel Core i5-2320中央处理器,4 GB内存计算机,预装Windows 7 64位旗舰版操作系统.其中,XDMR压缩算法分为MR预处理和多上下文模型的算术编码过程,简记为Pre和XDMRC.

实验1 测试预处理对MR数据压缩效果的影响.实验采用PPMd、PAQ8L、XDMRC、GZIP、LZMA和PPMd+pre、PAQ8L+pre、XDMRC+pre、GZIP+pre、LZMA+pre对3组原始的MR数据平均压缩情况、预处理前后的压缩率和相对压缩率RC进行对比.RC=(Sorigi-Spre)/Spre,其定义了相对压缩率MR数据平均压缩情况,表示压缩算法采用预处理相比未采用预处理压缩效果的相对提升程度,Sorigin表示对未经预处理MR压缩后的文件大小,Spre表示对预处理的MR压缩后的文件大小.如图3所示,左斜线柱和右斜线柱分别表明未经预处理的压缩算法和预处理的压缩算法针对3组MR数据的平均压缩率.在未经预处理的压缩算法中,PAQ8L和XDMR对MR压缩效果较明显,平均压缩率分别为18.27%和24.51%,RAR压缩效果最差,平均数据压缩率为37.56%.对采用预处理的压缩算法中,PAQ8L+pre和XDMRC+pre算法的数据压缩效果相对较好,平均数据压缩率是13.09%和14.59%,bzip2+pre和RAR+pre算法的数据压缩相对较差,平均数据压缩率是20.97%和19.99%.未加预处理和结合预处理的压缩算法对MR数据压缩率的变化,表明所列的压缩算法结合文中所提出的预处理方法能够有效提升MR数据压缩率.交叉线柱图是对比两种方式的相对压缩率,表明预处理过程对MR数据压缩提升效果的量化数据.各压缩算法采用预处理对MR数据的相对压缩率在28.38%～46.84%之间,提升效果明显.

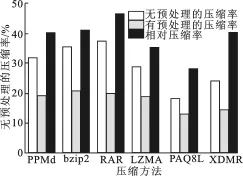
图3　预处理方法对MR数据压缩效果

实验2 测试对比预处理方法和未采用预处理方法以及MR文件大小与压缩率的变化关系.实验2与实验3均是压缩大小为5 MB、10 MB、15 MB、20 MB的12个MR数据,每组有3个MR文件,压缩率是每组平均压缩率.如图4所示,无预处理的压缩算法对MR数据的压缩率随文件大小变化的曲线是基本上平行横坐标的直线,可认为压缩率是恒定的数值.这说明无预处理的压缩算法,压缩率与文件大小的关系是恒定不变的.与此不同的是,从采用预处理的压缩算法对MR的压缩率与MR大小的变化曲线可以看出,MR数据的压缩率随MR文件的增大而变小.例如,PPMd+pre在4类大小不同数据的平均压缩率取值分别是20.78%、19.65%、19.29%、19.09%,其中,5 MB大小的数据文件压缩率最高,20 MB大小的数据文件压缩率最低.压缩率的降低原因是MR文件越大,存在冗余的报文可能性越增多.因此,采用预处理的压缩算法的特点之一是MR数据的压缩率随文件大小缓慢降低,这也是未采用预处理的压缩算法所不具备的特点.

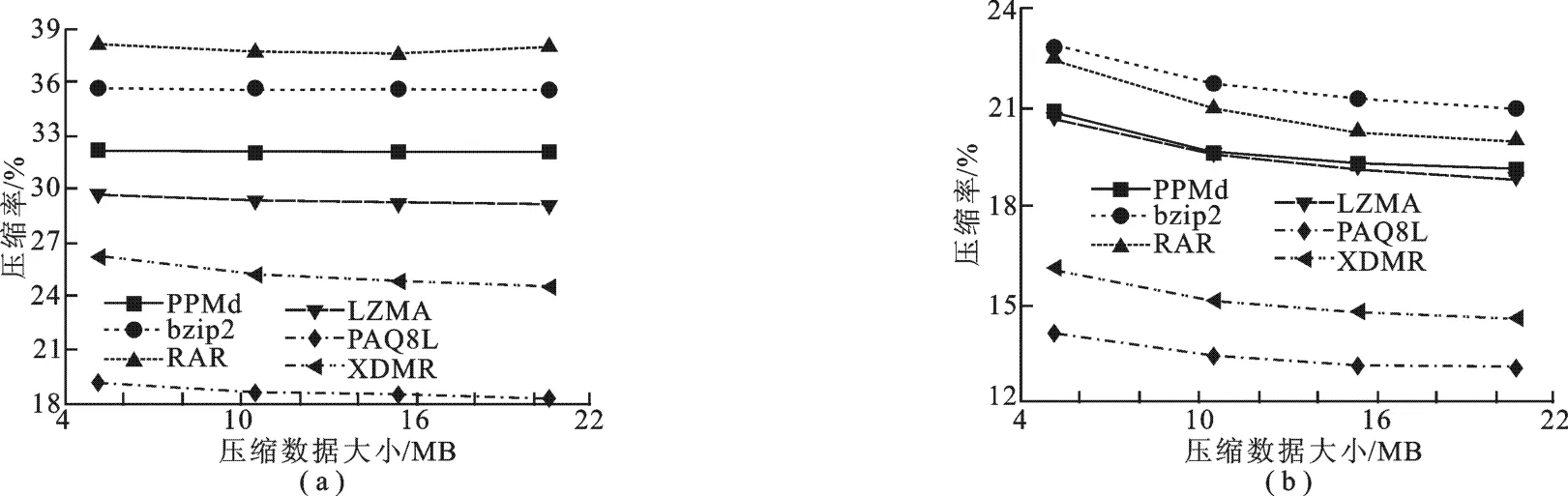
图4　预处理方法和未采用预处理方法数据大小与压缩率的变化关系

实验3 对比未采用预处理与采用预处理的压缩算法消耗的压缩时间.如图5所示,PAQ8L和PAQ8L +pre消耗的压缩时间是未采用预处理和采用预处理的压缩算法中耗时最长的,所有的压缩算法的压缩耗时,都随文件增大而增大.图5表明采用预处理压缩算法比未采用预处理的压缩算法对于同样大小的MR文件的压缩耗时少,采用预处理的压缩算法减少了冗余信息的距离,而且减少了冗余信息的匹配次数,因此,采用预处理的压缩算法的消耗的压缩时间少于未采用预处理过程的压缩算法.从3组实验可知,XDMR是较为理想的测量报告压缩算法.

3　结束语

笔者提出了基于谱分析的测量报告压缩算法.该算法提出了MR数据谱分析的方法,并利用分析结果对MR数据进行两次排序,再利用神经网络对测量报告建立上下文.实验结果表明,在采用压缩算法后,压缩时间明显减小,压缩率随被压缩数据的增大而减小,对测量报告的压缩效果结果明显.

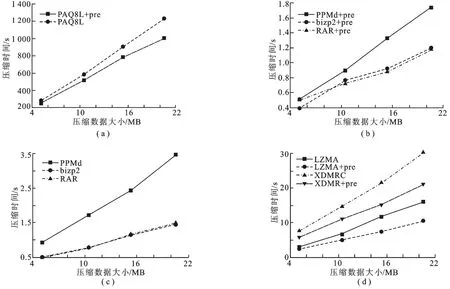
图5　未采用预处理与采用预处理的压缩算法消耗的压缩时间

[1]AL R Y,KARMOUCH A.QoS-Based Composition of Service Specific Overlay Networks[J].IEEE Transactions on Computers,2015,64(3):832-846.

[2]ZIV J,LEMPEL A.A Universal Algorithm for Sequential Data Compression[J].IEEE Transactions on Information Theory,1977,23(3):337-343.

[3]CLEARY J G,WITTEN I H.Data Compression Using Adaptive Coding and Partial String Matching[J].IEEE Transactions on Communications,1984,32(4):396-402.

[4]SHKARIN D.PPM:One Step to Practicality[C]//Data Compression Conference Proceedings:2002.Piscataway: IEEE,2002:202-211.

[5]STEINRUECKEN C,GHAHRAMANI Z,MACKAY D.Improving PPM with Dynamic Parameter Updates[C]//Data Compression Conference Proceedings:2015.Piscataway:IEEE,2015:193-202.

[6]MAHONEY M.Adaptive Weighing of Context Models for Lossless Data Compression[R].Melbourne:Florida Institute of Technology,2005.

[7]SEWARD J.On the Performance of BWT Sorting Algorithms[C]//Data Compression Conference Proceedings:2000. Piscataway:IEEE,2000:173-182.

[8]BRISABOA N R,CERDEIRA-PENA A,NAVARRO G.XXS:Efficient XPath Evaluation on Compressed XML Documents [J].ACM Transactions on Information Systems,2014,32(3):13.

[9]刘凯,李云松,郭杰.高性能EBCOT编码加速算法及其实现结构[J].西安电子科技大学学报,2010,37(4): 587-593. LIU Kai,LI Yunsong,GUO Jie.High Performance EBCOT Algorithm and VLSI Architecture[J].Journal of Xidian University,2010,37(4):587-593.

[10]STRUTZ T.Adaptive Context Formation for Linear Prediction of Image Data[C]//IEEE International Conference on Image Processing.Piscataway:IEEE,2014:5631-5635.

[11]STRUTZ T.Entropy Based Merging of Context Models for Efficient Arithmetic Coding[C]//IEEE International Conference on Acoustics,Speech and Signal Processing.Piscataway:IEEE,2014:1991-1995.

[12]ACETO G,BOTTA A,PESCAPÉA,et al.Efficient Storage and Processing of High-volume Network Monitoring Data [J].IEEE Transactions on Network and Service Management,2013,10(2):162-175.

(编辑:齐淑娟)

Spectrum analysis compression algorithm of measure report data

CHENG Fei,LIU Kai,DING Wenwen,SHI Huan,ZHANG Baijian
(School of Computer Science and Technology,Xidian Univ.,Xi’an 710071,China)

To solve to the problem that with the increment of the number of mobile users,the network bandwidth cannot meet the mass transfer of the measure report.This paper defines the conception of the spectrum of the measure report and proposes a spectrum analysis compression algorithm for the measure report.The algorithm utilizes two step sorting in order to reduce the distance between similar contents according to the analysis of the spectrum of measure report data.Furthermore,this algorithm employs several context models,which are regarded as the input nodes of the neural network.The prediction probability is calculated by the linear combination of the probability of each context model,and the weight in each link is tuned by the next bit in order to increase the possibility of matching.Experimental results reveal that the algorithm not only decreases the compression consuming time,but also ascends the compression ratio with the increment of the size of compression data.Compared with other competitors,this algorithm can effectively increase the compression ratio of the measure report to gain a better transfer time.

measure report;data compression;spectrum analysis;neural network

TP391

A

1001-2400(2016)04-0178-06

10.3969/j.issn.1001-2400.2016.04.031

2015-10-19

国家自然科学基金资助项目(61571345,61550110247);中央高校基本科研业务费专项资金资助项目(BDY191420);安徽省高等学校自然科学研究资助项目(KJ2014B14)

程 飞(1985-),男,西安电子科技大学博士研究生,E-mail:chengfei8582@163.com.