时差定位最优布站方法研究
2016-12-06黄高明
周 成,黄高明,高 俊
(海军工程大学电子工程学院,湖北武汉 430033)
时差定位最优布站方法研究
周 成,黄高明,高 俊
(海军工程大学电子工程学院,湖北武汉 430033)
针对时差定位,提出了以优化布站来提升定位精度的方法.该方法以克拉美罗下界的迹最小为定位精度衡量指标,通过对时差定位条件下克拉美罗下界的影响因素进行分析,发现接收站到目标的距离对克拉美罗下界没有影响,而接收站到目标的角度对克拉美罗下界有影响.随后,对克拉美罗下界迹的表达式进行了推导,并求得其最小值及取最小值的条件,得到结论:当接收站包围目标并呈等角布站时,对目标定位的克拉美罗下界取得最小值,此时布站最优.
无源定位;时差定位;布站;克拉美罗下界
如何提高无源时差定位系统的定位精度,一直以来是研究的重点问题.时差定位(Time Differences Of Arrival,TDOA)[1-4]的精度不仅受到定位算法的影响,无源定位接收站的布置更是决定了一切定位算法所能达到的最优性能[5].对于一个无偏的估计器,其性能可以由其是否达到或逼近克拉美罗下界(Cramer-Rao Lower Bound,CRLB)来表征.克拉美罗下界由费舍尔信息矩阵(Fisher Information Matrix,FIM)求逆得到,其代表了目标位置估计最小的方差值[6].
近年来,无源定位接收站的布置得到了广泛的研究.文献[5]中对到达角度(Angle Of Arrival,AOA)定位[7-8]、到达时间(Time Of Arrival,TOA)定位[9-10]、接收信号强度(Received Signal Strength,RSS)定位[11]情况下的最优布站进行了研究,提出了上述定位体制下,不同接收站数目时的最优布站方法.针对时差定位,文献[6]中提出了理想情况下(任意接收站可布置在任意位置)的时差定位布站理论,在随后的研究中,对于不同的定位环境,提出了不同的布站策略[12],以使得克拉美罗下界的迹最小.文献[6]在时差定位布站的理论推导过程中,为了使推导的方程得到简化,将协方差矩阵简化为单位矩阵进行处理,但在实际的时差定位系统中,由于以同一个接收站为参考站的测量值都会包含该参考站的测量误差,因此,这些测量值是彼此相关的,在文献[6]中的简化处理是不合理的.
针对时差定位最优布站问题,以克拉美罗下界的迹最小为优化准则,笔者首先对时差定位体制下克拉美罗下界的影响因素进行了分析,并指出接收站到目标的距离对于克拉美罗下界没有影响,而接收站到目标的角度对克拉美罗下界有影响.接着,考虑到时差定位测量值是由参考站和非参考站之间的到达时间测量值相减得来的,因此时差定位测量值之间具有相关性,故在最优布站的理论推导过程中采用了一个更具一般性的协方差矩阵[13].在此基础上,计算出了克拉美罗下界迹的表达式,并推导出其取得最小值的条件,得到了时差定位最优布站的形式.
1 无源时差定位模型
考虑在二维平面内的定位问题.设有M个接收站,每个接收站的位置是已知的,表示为i=1,2,…,M.其中,(*)o表示含噪量(*)的真实值.设定第1个接收站为参考站.假设目标的位置为uo, uo=[x,y]T.目标到达接收站i与到达接收站1的距离差,i=2,3,…,M.其中表示第i个接收站到目标的距离,表示求二范数运算.假设第i个接收站到目标的方位角为φi,那么存在如下的表达式:

在实际应用中,观测得到的时差定位ti1中存在测量噪声误差.当信号传播速度恒定时,距离差与时差定位之间呈比例关系,则观测到的距离差ri1可以表示为
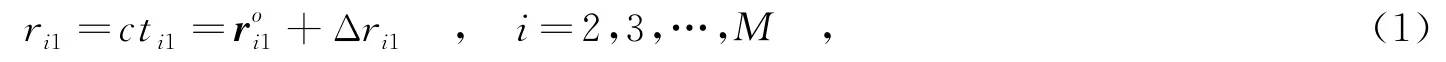
其中,c是信号传播的速度,ri1是含噪的距离差值,Δri1是测量误差.为了方便表示,将式(1)改写成向量的形式:r=ro+Δr,其中,,Δr=[Δr21,Δr31,…,ΔrM1]T.同样地,将接收站表示成一个M×2的矩阵:
时差定位问题即是在已知接收站的位置so和含噪的距离差r的情况下,对目标的位置uo进行估计.
2 克拉美罗下界分析
克拉美罗下界是任何无偏估计量所能达到的下界,它能够检验无偏估计量的性能.克拉美罗下界可以通过费舍尔信息矩阵的逆来表示[14]

其中,J表示费舍尔信息矩阵,
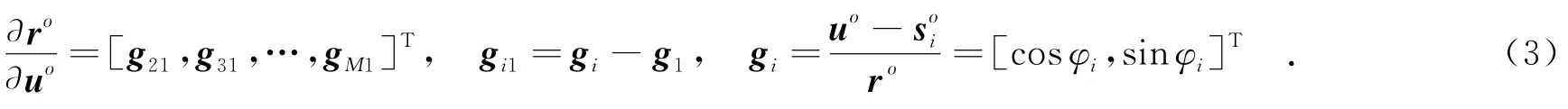
其中,gi是一个二维单位向量,其值分别是接收站指向目标方位角的余弦值和正弦值.从式(2)和(3)可以看出,克拉美罗下界主要受到两个因素的影响:测量误差通过协方差矩阵Q对其进行影响,且测量误差越小,克拉美罗下界也越小;各接收站与目标之间的位置关系,通过分析gi可以得到,接收站与目标之间的距离对于克拉美罗下界没有影响,只有角度对其有影响.
3 时差定位布站研究
在时差定位问题中,目标与接收站之间的位置关系由so和uo决定.克拉美罗下界的迹表示了无偏的目标位置估计量在各个维度上方差的和,工程中,一般以它来衡量目标定位性能[14].下面考虑在理想条件下,如何使得克拉美罗下界的迹最小,达到最优布站.
假设各个接收站对目标的测量噪声是独立同分布的,都服从于均值为零、方差为σ2的正态分布.非参考站与参考站之间的时差定位测量值由相应的一对到达时间值相减产生,因此时差定位测量噪声是相关的,其协方差为[13]

式(3)中,IM-1表示(M-1)×(M-1)维的单位矩阵,1M-1表示M-1维的列向量.根据Woodbury公式,Q的逆可以表示为

在全受控站条件下,时差定位最优布站问题就是要找到M个单位向量gi,使得tr(J-1)最小.要使得tr(J-1)达到最小值,等价于tr(J)达到最大值,而后者在形式上不需要求逆运算,较简便.下面,先对tr(J-1)与tr(J)的关系进行推导,再求取tr(J)的最大值及达到最大值的条件.
由式(3)并结合克拉美罗下界的定义可知,J是一个2×2的正定矩阵,假定其两个特征值分别为μ和η,有μ>0、η>0.J-1的特征值为1/μ、1/η.一个矩阵的迹就等于其所有特征值之和,因此有tr(J)=μ+η, tr(J-1)=1/μ+1/η.根据柯西施瓦茨不等式,有

且当μ=η时,式(5)可取得等号.
下面,求取tr(J)的最大值及达到最大值的条件.将Q-1的表达式(4)代入J,得
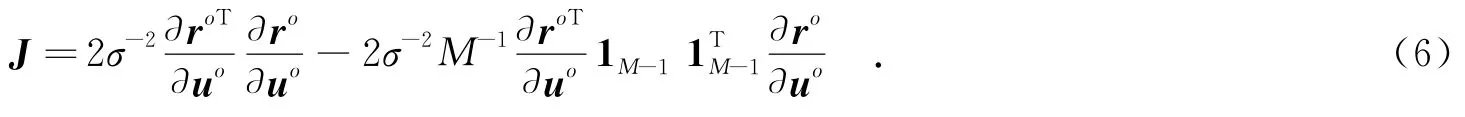
式(3)可以进一步简化为

将式(7)和式(8)以及gi=[cosφi,sinφi]T代入式(6),并经过直接的计算,得

对式(9)求迹,得
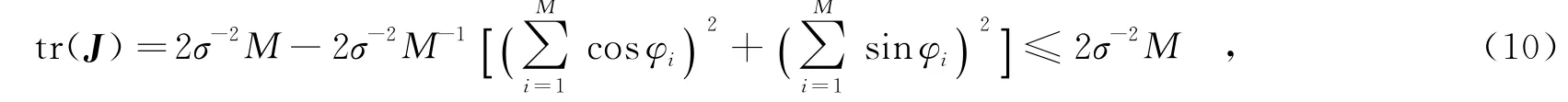
4 仿真实验分析
为了验证全部接收站受控情况下的时差定位最优布站,设计仿真实验如下.采用8个站,对未知的目标进行定位,假定目标的位置位于原点,选取了4种布站形式对目标进行定位,分别是:①包围目标的等角布站形式;②所有接收站位于目标一侧;③所有接收站均匀分布在目标两侧;④所有接收站分布在目标的三面.由于接收站到目标的距离对克拉美罗下界没有影响,因此假定所有接收站位于同一单位圆上.在不同的布站形式下,每个接收站到目标的角度如表1所示.在这4种不同的布站形式下,将σ2从-30 d B增大到30 d B,分别计算4种布站形式下目标定位的克拉美罗下界值,其结果如图1所示.

表1 不同布站形式下接收站到目标的角度值
从图1可以看出,随着接收站的布置从目标的一侧扩展到两侧、三面,克拉美罗下界逐渐减小.当等角布站时,克拉美罗下界比另外3种布站形式小1 dB到7 B不等.

图1 不同布站形式下克拉美罗下界的比较
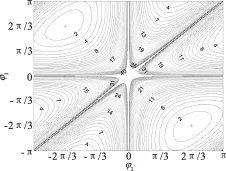
图2 接收站到目标角度值的变化对克拉美罗下界的影响
为了对理想环境下所有接收站包围目标并呈等角布站是时差定位最优布站这一结论进行充分验证,进行如下仿真实验.设置σ2为0 dB,有3个接收站,其中第1个接收站指向目标的方位角φ1(φ1=0),第2个接收站和第3个接收站指向目标的方位角φ2和φ3,将φ2和φ3在[-π,π)上进行遍历,可以得到克拉美罗下界随接收站布置的变化图,如图2所示.从图2中可以看出,当φ2=-2π/3和φ3=2π/3或φ2=2π/3和φ3=-2π/3时,3站即成等角布站,克拉美罗下界取得最小值.
5 结 论
以克拉美罗下界的迹最小为最优准则,对时差定位最优布站方法进行了研究.通过对克拉美罗下界的表达式进行分析推导,并求得其迹的最小值,得出如下结论:在理想条件下,接收站包围目标并呈等角布站是时差定位最优布站形式.但是在实际中,大部分站是固定不动的,往往只有少数的站能够移动.下一步,将针对该类问题开展研究工作.
[1]HUANG B Q,XIE L H,YANG Z.TDOA-based Source Localization with Distance-Dependent Noises[J].IEEETransactions on Wireless Communications,2015,14(1):468-480.
[2]EI-GEMAYEL N,JAKEL H,JONDRAL F K.Error Analysis of a Low Cost TDo A Sensor Network[C]//2014 IEEE on Position,Location and Navigation Symposium.Piscataway:IEEE,2014:1040-1045.
[3]CHAKRABORTY J,OTTOY G,GELAUDE M,et al.Acoustic Localization of Unknown Sources with Wireless Sensor Nodes[C]//2014 17th International Conference on Computer and Information Technology.Piscataway:IEEE, 2014:488-493.
[4]朱国辉,冯大政,周延.一种多参考接收站下的时差定位算法[J].西安电子科技大学学报,2014,41(4):31-35. ZHU Guohui,FENG Dazheng,ZHOU Yan.TDOA Location Algorithm Based on Multi-reference Receivers[J]. Journal of Xidian University,2014,41(4):31-35.
[5]BISHOP A N,FIDAN B,ANDERSON B D.Optimality Analysis of Sensor-target Localization Geometries[J]. Automatica,2010,3(46):479-492.
[6]YANG B,SCHEUING J.Cramer-Rao Bound and Optimum Sensor Array for Source Localization from Time Differences of Arrival[C]//Proceedings of the IEEE International Conference Acoustics,Speech and Signal Processing:4. Piscataway:IEEE,2005:Ⅳ961-Ⅳ964.
[7]BISHOP A N,FIDAN B,ANDERSON B D.Optimality Analysis of Sensor-target Geometries in Passive Localization: Part 1-Bearing only localization[C]//Proceedings of the International Conference on Intelligent Sensors,Sensor Networks and Information Processing.Piscataway:IEEE,2007:7-12.
[8]STEPHAN H,MARTIN K,REINER T,et al.Selection of Antenna Array Configuration for Polarimetric Direction Finding in Correlated Signal Environments[C]//Proceedings of 19th International ITG Workshop on Smart Antennas. Piscataway:IEEE,2015:1-8.
[9]BISHOP A N,FIDAN B,ANDERSON B D.Optimality Analysis of Sensor-Target Geometries in Passive Localization: Part 2-Time-of-Arrival Based Localization[C]//Proceedings of the International Conference on Intelligent Sensors, Sensor Networks and Information Processing.Piscataway:IEEE,2007:13-18.
[10]丰大军,许录平,宋诗斌,等.利用X射线脉冲星的星间差分联合定位算法[J].西安电子科技大学学报,2014,41 (1):81-86. FENG Dajun,XU Luping,SONG Shibin,et al.Differential Co-localization Method Using the X-ray Pulsar[J].Journal of Xidian Univercity,2014,41(1):81-86.
[11]BISHOP A N,JENSFELT P.An Optimality Analysis of Sensor-Target Geometries for Signal Strength Based Localization[C]//Proceedings of the International Conference on Intelligent Sensors,Sensor Networks and Information Processing.Piscataway:IEEE,2009:127-131.
[12]YANG B,SCHEUING J.A Theoretical Analysis of 2D Sensor Arrays for TDOA Based Localization[C]//Proceedings of the 2006 IEEE International Conference on Acoustics,Speech and Signal Processing.Piscataway:IEEE,2006:58-63.
[13]HING C S.Closed-form Formulae for Time-difference-of-arrival Estimation[J].IEEE Transactions on Signal Processing, 2008,56(8):2614-2620.
[14]CHAN Y T,HO K C.A Simple and Efficient Estimator for Hyperbolic Location[J].IEEE Transactions on Signal Processing,1994,42(8):1905-1915.
(编辑:郭 华)
Optimum sensor array for passive localization from time differences of arrival
ZHOU Cheng,HUANG Gaoming,GAO Jun
(College of Electronic Engineering,Naval Univ.of Engineering,Wuhan 430033,China)
In the TDOA system,the method for improving the source location accuracy by sensor arrangement is proposed.The trace of the CRLB of a source estimate is the criterion.By analyzing the factors of the CRLB,it is found that the CRLB does not depend on the range between sensor and source, but on the direction from sensor to source.The expression for the trace of the CRLB is derived.Then its minimum value and the condition for achieving the minimum value are obtained.It is shown that the uniform angular array is the optimum sensor array when the source is surrounded by sensors.
passive localization;time differences of arrival;sensor placement;Cramer-Rao lower bound
TN97
A
1001-2400(2016)04-0123-05
10.3969/j.issn.1001-2400.2016.04.022
2015-04-17 网络出版时间:2015-10-21
国家自然科学基金资助项目(60901069);国家“863”计划资助项目(2013AAXXXX061)
周 成(1986-),男,海军工程大学博士研究生,E-mail:zhouchengscholar@163.com.
网络出版地址:http://www.cnki.net/kcms/detail/61.1076.TN.20151021.1046.044.html
