上市公司企业绩效测度与评价

刘冰+李长军

内容摘要：本文从与企业绩效相关的变量出发，综合国内外相关文献，介绍回归方法的基本概念。基于制造业上市公司财务数据，研究分析与企业绩效相关的24个变量，分别使用最小二乘法、相关系数法、岭回归、最优子集选择法和lasso方法进行回归，根据回归结果比较不同方法的优劣处，综合选择最优的回归方法得到最优的模型为lasso模型，并解释模型，通过交叉验证的方法进行验证分析。最后通过模型提出建议：优化高管结构，根据行业特征选择最优企业模型，保证审计意见准确，并且由于公司规模较大后规模报酬递减，因此在公司规模扩大到一定程度后应停止扩张。

关键词：企业绩效   岭回归   最优子集选择法   lasso   交叉验证

问题的提出

（一）研究背景

本文旨在从众多变量中筛选出有价值的变量，利用筛选出的变量进行企业绩效的相关性分析，以期发现实际意义。本文区别于传统的根据专家选择解释变量建立回归模型的方法，而将挑选和企业绩效相关的因素的过程引入到建模。基于2015年制造业上市公司财务数据，研究分析与企业绩效相关的24个变量，分别使用最小二乘法、最优子集选择法、岭回归和lasso方法进行分别回归，根据回归结果比较不同方法的优劣处，综合选择最优的模型并解释模型。最后通过交叉验证的方法进行验证分析。

本文在使用最小二乘法、最优子集选择法、岭回归和lasso算法后分析比较得出，lasso算法无论是在变量选择还是拟合优度方面都表现得更为出色。根据研究过程，本文也针对企业绩效提出相关建议。

（二）数据来源及样本处理

本文选用制造业上市公司2015年公开披露的财务数据1686个，在此基础上做了如下处理：删除ST、*ST企业的样本;删除相关变量缺失的企业样本，最终得到了1006个企业年度数据，为消除离群值的影响，对所有连续型变量进行了（1%，99%）的缩尾处理。本文数据均来自国泰君安数据库。

本文用ROA表示企业绩效，同时选取24个可能与它相关的变量，分别是董事会效率、董事会独立性、公司规模、公司年龄、市净率、比率结构（有形资产比率、无形资产比率）、主营业务利润占比、财务杠杆、总股数、国有股占比、资产负债率、归属于上市公司股东的扣除非经常性损益的净利润、加权平均净资产收益率、基本每股收益、审计意见、内控评价报告（是否披露内控评价报告、是否出具内控评价报告结论、内部控制是否有效、内部控制是否存在缺陷）、高管资料（年龄、教育背景、年末持股数）、公司年龄。

企业绩效模型建立与实证分析

（一）最小二乘模型

本文采用最小二乘法为对照组，用以比较其它回归方法得到的结果，并从中选出最优模型。说明：所有数据已进行了标准化处理，所以模型的系数大小说明的是比例，与量纲无关。在最后做出预测时，只需根据均值和标准差进行还原即可。关于目标函数求得最小二乘解和显著性检验结果，如表1所示。

从回归的结果可以看出，大部分变量的系数不能通过显著性检验，说明回归的结果不佳，模型里掺杂了很多不相关的变量。

加权平均净资产收益率、资产负债率等指标能较为直接的反映企业绩效，因为它们是与企业绩效直接相关的变量。需要引起关注的是显著变量中的审计意见类型、高管年龄和高管持股数，其对企业绩效产生了显著的影响。

（二）最优子集选择模型

最优子集选择法的思想是对p个变量的所有可能组合分别使用最小二乘回归进行拟合，最后在所有可能模型中选择一个最优模型。

将最优子集选择法运用财务数据中，可以看到对于24个变量，模型中的变量数k的选择也有24种，对于每个k都有一个最优的模型。先对k=1，2，…，24分别选出最优模型，最后综合选出这24个不同的k的最优模型。模型误差与k的关系如图1所示。

从图1中可以看出，当模型的变量个数k取4时，模型的测试误差达到了最小值，此时的模型正是所要求的模型。且当模型中变量个数很大时，模型的误差大大增加，即达到拟合状态。

在最优子集选择法中保留下来的变量为市净率、资产负债率、净资产收益率、基本每股收益。这样的结果是有说服力的，因为这四个变量都可以作为企业绩效的直接体现，同时也得到一个结论，模型的准确性极高，解释性极强。但并不能作为很有意义的信息，以提出有效的结论。所以应当增加模型中的变量数，找出与企业绩效非直接相关的变量，当模型的变量增加到5个时，公司规模加入了模型;当变量增加到6个时，审计意见类型又加入了模型。

公司规模的系数为负数，即公司规模越大，企业绩效越差，这显然与显示情况不完全相同。直接观察公司规模和企业绩效的关系如图2所示。

公司规模与企业绩效有较明显的相关关系，即公司规模与企业绩效的关系是一个较为明显的倒U凹函数。在短期内小幅度增加公司规模对于企业绩效有一个有益的促进，由斜率可以看出，公司规模的扩大会使企业绩效快速发展，但这只在小规模企业成立;当企业规模渐渐扩大时，企业绩效不再呈增长趋势，而是缓缓下降，也由斜率可以看出，企业绩效的下降速度较缓慢。

审计意见被证明是一个和企业绩效显著相关的变量。由于审计意见变量是个定性变量，因此在回归时当作哑变量来处理，并且赋予审计意见得分（见表2）。

审计意见类型对企业绩效有着显著的影响，处理数据得到的审计意见得分是根据审计意见类型的优劣来排序的。对于审计意见得分这个变量，企业绩效的最优子集选择的系数显著为正。只有科学的结构和良好的企业绩效才会得到审计者的信任，因此公司绩效的好坏是与审计意见类型直接相关的。可以说，企业绩效良好的企业会更容易得到给出审计意见类型的注册会计师的信任，并且审计意见类型良好的企业所给出的报表更加真实公允不做假，这样的企业一般信誉较高，所以对公司绩效有一个正的作用。

（三）岭回归模型

岭回归的目标函数为，从目标函数可以看出，它与最小二乘最大的不同是加入了一项，称为压缩惩罚，当β1、…、βp接近零时比较小，因此具有将βj的估计值往零的方向进行压缩的作用。当λ=0时，惩罚项不产生作用，岭回归与最小二乘估计结果相同。随着λ→∞，压缩惩罚项的影响力增加，岭回归系数估计值越来越接近零。与最小二乘法得到的唯一的估计结果不同，岭回归得到的系数估计结果βRλ随λ的变化而变化。

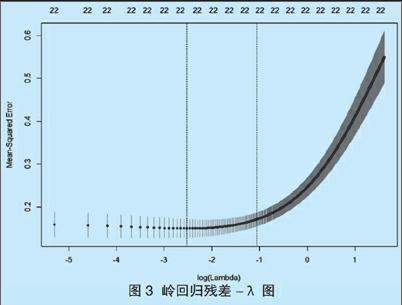
从λ取值从0到5，等距取1000个值。图3直接给出了在不同λ下的岭回归对企业绩效的估计值和企业绩效真实值之间的误差。

从图3中可以看出，在参数λ位于虚线之间时，残差平方和达到最小，即岭回归效果最好。在λ较小时，误差一致处于较低的水平，但是当λ超过某个值后，误差迅速增加。这是由于当λ变得过大时，惩罚项的作用太大，以至于在求解目标函数最优解时忽略了残差平方和。通过十折交叉验证法，可以求出建模效果最好的λ的取值。

综上所述，岭回归效果最好时，则存在λ=0.08008008。即在λ=0.08008008时岭回归所得的模型最优。由于篇幅所限，岭回归系数在此不一一列出，但通过结果能够发现，岭回归过程没有实现筛选一些与企业绩效显著相关的变量的效果，而是将所有可能与企业绩效相关的变量系数整体压缩后得到回归结果。但同时岭回归仍然提升了最小二乘估计的效果。岭回归的劣势在于它的复杂度惩罚项可以将系数往0的方向进行缩减，但是不会把任何一个变量的系数确切的压缩至0（除非λ=∞）。本文将进一步使用lasso方法来解决这个问题。

（四）lasso模型

lasso是近年来常用的用于克服岭回归上述缺点的方法。lasso的系数βLλ通过求解目标函数得到。比较lasso和岭回归的目标函数，可以发现它们具有相似的拟合公式。唯一的区别是岭回归中的β2j项在lasso中被替代为上式中的|βj|。与岭回归相同，lasso也将系数估计值向0的方向进行缩减。当调节参数λ足够大时，它的惩罚项具有将其中某些系数的估计值强制设定为0的作用。因此，lasso建立的模型与岭回归建立的模型相比更易于解释。研究中，lasso起到的作用和最优子集选择法较为相似，即把与企业绩效显著相关的变量筛选出来。

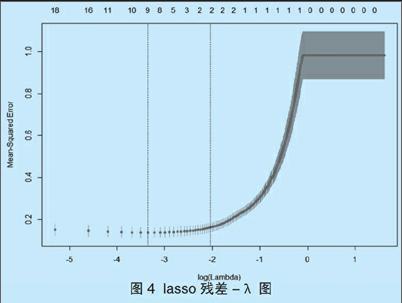
与岭回归的步骤相同，首先应选定合适的参数λ，使得模型的交叉验证集误差最小，从图4中可以看出，参数λ在两条虚线之间时达到最优模型，此时λ=0.03503504，相比较岭回归而言，lasso的参数λ较小，说明收缩程度并不大，但仍然达到了筛选变量的效果。最优模型的系数如表3所示。

最终选出的变量有资产负债率、归属于上市公司股东的扣除非经常性损益的净利润、加权平均净资产收益率、基本每股收益、公司规模、高管年龄、高管年末持股数七个变量。其中可以得到关于企业绩效有效的结论和提升企业绩效的建议的变量有公司规模、高管年龄、高管年末持股数这三个变量，因为剩下的四个变量可以直接表示企业经营状况，并不能提供建议。

公司规模显然是一个与企业绩效相关的变量，因为它在最优子集选择法和lasso中都被显著挑选出来作为企业绩效的解释因素。从前面的分析中可知，公司规模对于企业绩效在短期内应该是正相关的关系，但在公司规模扩大到一定程度后，再进行扩张就会使企业绩效向相反方向变动。在信息完全且不考虑企业内部腐败成本的情况下，理论上的公司规模的扩大会使生产、加工、管理、损耗都成规模，产品规格标准化，大量购入原材料致使单位成本下降，管理人员技术人员生产方案和资源分配的选择更多，显然会比公司规模较小时达到更优的帕累托最优状态。但现实中的市场是不完全的市场，企业规模扩大到某种程度会让生产管理成本都飞速增加，在大企业中也很难实现像小企业一样的面面俱到的监督管理。

高管年龄和高管年末持股属于企业的高管特征变量。从系数可以看出，高管年龄对企业绩效呈显著的弱正相关关系，高管年末持股数与企业绩效呈现较强的正相关关系。与过去较为封闭保守的市场环境不同，年龄较大且经验丰富的管理者，比年轻的管理者对于企业绩效的提升而言，优势并不明显，因为我国市场已经步入转型期，机遇增多，高管年龄对于企业绩效不再是一个至关重要的因素，但工作经验仍然是优势。对于高管年龄的研究也很丰富， Wiersema M F和Bantel K A等认为，高管年龄的多样化程度高，异质性较大，与企业绩效负相关;而高管年龄的同质性较高对企业绩效有正面影响但作用不大，这也与本文得到的显著弱正相关关系一致。

高管年末持股数与企业绩效呈现显著正相关关系。每增加0.01%的高管持股数，企业绩效可以增加0.05%。高管的持股比例奖励会引发激励效应。但企业的高管持股比例普遍较低，这会影响激励效应的发挥;其次，很多企业的高管持股比例数据为零，即并无正式的股权激励政策，没有对所有高管人员进行股权激励，因此激励效果也会大打折扣。

模型比较与政策建议

（一）模型结果比较

不同的模型有各自的优缺点。例如最小二乘法会引入很多不显著相关的变量，信息冗杂，给影响企业绩效的真实因素带来了噪声影响;最优子集选择法是一种不解析、不连续的方法，它对于系数的收缩不是循序的，估计结果的方差极大，数据有一点差异可能会给结果带来很大的改变;岭回归方法克服了最优子集选择法不连续的缺点，它实现了系数的连续变化，但是不能将一些变量的系数直接收缩到零;lasso是介于岭回归和最优子集选择法之间的一种方法，不仅实现了算法的连续，并且它的解是稀疏的，即能够将部分变量筛掉。表4给出了在研究企业绩效相关性问题上运用这几种方法的效果。

由结果可以看出，所采用的三个降低模型复杂度的回归方法的确在最小二乘法的基础上改善了很多，在对企业绩效的预测方面比原本的精度提高了5%以上，lasso算法甚至将精度提高了10%，其中最优子集选择法和岭回归的回归效果相似，但是最优子集选择法只使用了6个变量（市净率、资产负债率、净资产收益率、基本每股收益、公司规模、审计意见类型）评价企业绩效的预测，而岭回归使用了24个变量，所以在评价最优子集选择法比岭回归更有意义。而lasso无论是在变量选择和回归精度方面的表现都更加出色。它只用了资产负债率、归属于上市公司股东的扣除非经常性损益的净利润、加权平均净资产收益率、基本每股收益、公司规模（总股数）、高管年龄、高管年末持股数7个变量就使预测精度提高到75%，说明lasso模型更有意义。

（二）政策建议

公司规模与企业绩效息息相关，在短期内，企业规模的扩大能够实现生产或经销单位成本的降低，处于规模报酬递增状态，但当公司规模扩大到一定程度后会处于规模报酬递减状态，应稳定企业发展，因此绝不能一味盲目扩大规模。

审计意见类型良好的企业所给出的报表应更加真实，从而有较高的信誉，审计意见类型可以一定程度上反映企业的经营和诚信状况。审计意见类型指标较技术性的指标处在一个更加重要的地位，所以相比较企业的经营方式、营销手段等技术指标，更应注意企业的诚信建设。

高管特征在研究中处于重要地位。lasso方法选出的三个变量中有两个是高管特征变量，因此应当注意培养人才留住人才，管理人员是企业命脉，适当选择经验丰富的经理人，保证管理阶层的同质性，少追求管理阶层年龄和教育背景的多样化。

尤为重要的是对管理人员适当采取股权激励机制。虽然高管的持股比例很小，但对其实施股权激励将会发挥巨大的作用，当经理人股权达到一定数目后，不仅能够提高忠诚度，还能监督治理企业内部腐败。