劳动力老龄化的均衡与过渡动态效应

刘琪+袁蓓

内容摘要：本文收集了1982-2010年我国劳动年龄人口结构、物质资本投资率、人均人力资本存量、人口增长率等宏观经济变量各省数据资料，在扩展的经典经济增长模型基础上，运用固定时期效应（FE）和广义矩估计（GMM）检验了劳动力老龄化的均衡与过渡动态效应。结果表明，劳动力老龄化将引起我国均衡人均收入下降和增长减缓。据此建议，通过扩大就业、渐近延长退休年龄、提高人口质量等措施，提升劳动力利用效率，挖掘人口潜力，保障经济持续增长。

关键词：劳动力老龄化   均衡GDP   过渡动态增长率   GMM估计

改革开放以来，我国经济的持续高速增长在很大程度上得益于丰富的劳动力资源。然而，随着人口老龄化程度不断加剧，这一优势已逐渐丧失。研究表明，低生育率会引发劳动力数量不足，并造成高龄劳动力堆积。根据联合国《世界人口展望2015》统计，我国45-64岁老年劳动力的数量和比重分别为3.8亿和37.68%，逼近发达国家41.04%的平均水平，老年劳动力正成为我国劳动力队伍的主力。本文在充分利用我国1982-2010年历年人口普查和抽样调查数据的基础上，将劳动力年龄结构变量引入经典经济增长模型，通过理论与计量模型构建，分别从理论和实证两个方面研究了劳动力老龄化对我国均衡人均收入和过渡动态增长率的影响，并提出针对性政策建议。

理论模型

本文借鉴Lindth和Malmberg（1999）年的研究成果，通过将劳动力年龄结构指数M分别与人力资本h和就业量L相结合的方式，把劳动力年龄结构变量引入人均生产函数：

（1）

加入劳动参与率p和失业率μ之后，（1）式可改写为：

y=AkαhβM1-α[p（1-μ）]1-α-β    （2）

假设产出中用于物资资本和人力资本投资的份额都是固定的，分别为sk和sh，且上述两种资本的折旧率都为δ，人口以外生增长率n增长，解得均衡人均产出：

（3）

为具体化劳动力年龄结构指数M，假设各年龄段劳动力之间存在替代关系，且替代弹性为1，可构建C-D形式的劳动力年龄结构指数如下：

M=Πmi=1 xθii                                 （4）

xi为i年龄段劳动力占总人口的比例，θi为i年龄段劳动力的年龄指数弹性。

将（4）式代入（3）式，均衡人均产出为：

（5）

由（5）式可知，均衡人均产出由一系列基本参数决定，劳动力年龄结构也是基本参数之一。人均物资资本投资率、人均人力资本投资率、劳动参与率对均衡人均产出具有正向作用;人口增长率和失业率对均衡人均产出具有负向作用;各年龄段劳动力对均衡人均产出的作用方向取决于各自的年龄指数弹性系数θ的符号。

作为基础经济结构参数之一的劳动力年龄结构，其变化还会影响过渡动态增长率。根据Mankiw等（1992）对稳定状态线化方法的研究，可得到过渡动态人均产出增长率为：

其中，λ=（1-α-β）（n+δ），将（5）式代入上式，过渡动态人均产出增长率为：

（6）

（6）式揭示了过渡动态增长率与均衡人均产出间的关系。对比（6）式与（5）式不难发现，（6）式中各变量前系数的符号与（5）式中一致。这是因为，当基本参数引起均衡人均产出下降时，会缩短实际人均产出与均衡人均产出间的距离，造成过渡动态经济增长率下降，反之则上升。

实证模型与数据来源

（一）均衡效应计量模型

根据均衡人均产出解（5）式，可构建均衡人均产出计量模型如下：

lnyit=α0+α1lnsit+α2lnEit+

α3ln（n+δ）it+α4lnqnlrit+α5lnznlrit

+α6lnlnlrit+α7lnlcrit+α8lnyi，t-1+α9qyit

+εit                                                    （7）

被解释变量yit是均衡人均GDP，本文用各省人均实际GDP表示（1978=100）。由于人均实际GDP往往存在滞后影响，所以在解释变量中包含了人均实际GDP的滞后项，人均实际GDP较高的省份通常会继续保持高值，所以yi，t-1前的系数应为正。

解释变量中反映劳动力年龄结构的有三个，分别是青年劳动力、中年劳动力和老年劳动力占总人口的份额。根据国际劳工组织的划分，三类劳动力年龄范围分别为15-29岁、30-44岁和45-64岁，用pnlr1、znlr1和lnlr1表示（劳动年龄人口上限为60岁，但考虑到我国农村老年劳动力就业的普遍性以及城市社会保障力度有限，部分60岁以上老年人仍处于就业状态的事实，本文将劳动力年龄人口上限定为64岁）。劳动力年龄段划分的依据是劳动生产率，通常认为30-44岁是劳动生产率的高峰期，15-29岁是积累上升期，45-64岁为下降期。据此推断，青年劳动力与老年劳动力前的系数应为负，中年劳动力前的系数为正。在国际劳工组织划分的基础上，考虑到我国受教育年限延长、青少年就业率下降，以及人均寿命延长、健康程度提高、生产率高峰期年龄后移，将上述三类劳动力的年龄范围重新界定为20-34岁、35-49岁和50-64岁，并分别用pnlr2、znlr2和lnlr2表示。

（7）式中其余解释变量与理论模型中一致。sit为物质资本投资率，用固定资产投资占GDP的比值衡量。Eit为人均人力资本存量，用人均受教育年限衡量。劳动参与率lcr用第一、第二和第三产业的总就业人数占劳动年龄人口的比值表示。由于有关我国失业率的计量还存在不同观点，计算结果差距较大，故暂不考虑这一变量。考虑到我国四个直辖市的特殊情况，计量模型中引入区域虚拟变量qyit，将四个直辖市取值为1，其它省份和自治区为0。

（二）过渡动态效应计量模型

根据（6）式，可构造人均产出过渡动态增长率计量模型如下：

git=β0+β1lnsit+β2lnEit+β3ln（n+δ）it

+β4lnqnlrit+β5lnznlrit+β6lnlnlrit+β7lnlcrit+β8lnyi0+β9qyit+ωit                          （8）

（8）式中，被解释变量git是各省人均实际GDP增长率。已有研究证实，我国经济增长存在收敛性，因此（8）中各地区初始人均收入lnyi0前的系数为负，其余解释变量与（7）式相同。

（三）数据来源

现有研究较少将劳动力年龄结构变量引入经济增长模型，这一现象与我国劳动力年龄结构数据较难获得有关。全国人口普查和抽样调查提供了我国所有省份人口年龄结构详细数据，尽管调查年份和数据量有限，但还是为本文提供了宝贵资料。各年龄段劳动力人口数量、人均受教育年限、劳动参与率由1982-2010年四次全国人口普查、三次全国人口抽样调查资料计算整理得到。2010年之前的人均实际GDP及增长率、物质资本储蓄率和人口增长率由《新中国60年统计资料汇编》计算得到，2010年的数据来自《2010年中国统计年鉴》。

实证研究结果

本文数据具有截面成员较多，时期较少的“宽而短”的特点，适合采用面板结构模型。运用EVIEWS6.0计量软件作固定时期还是混合模型检验，F检验统计结果显示，时期固定效应模型是合理的。F检验统计量为10.126，且达到了99%以上的显著水平。尽管个体固定效应也可通过显著性检验，但经过反复对比后，模型回归系数在采用区域虚拟变量时更为合理，故模型采用区域虚拟变量，没有设定。

（一）均衡人均产出效应

计量模型（7）式中解释变量包含了被解释变量的滞后值，内生性问题不可避免，需要利用工具变量估计（IV）或广义矩估计（GMM）克服。本文采用Arellano和Bond（1991）提出的GMM估计法，将原模型一阶差分剔除个体效应，再利用被解释变量的初始值、当期值和滞后值均有可能成为差分模型解释变量的工具变量的性质，得到一些额外的工具变量。作为对照，本文同时给出了面板结构数据的固定时期效应（FE）估计结果，如表1所示。

首先，表1中的模型（2）、（4）、（6）采用了GMM估计法，过渡识别检验显示接受原假设，GMM估计使用的工具变量有效。AR（2）检验结果也表明，原模型一阶差分后的残差不存在二阶自相关，研究检验结果可信。模型（1）和（2）分别是基准增长模型的参数估计结果，固定效应与GMM估计得到变量符号与理论推断一致。实物资本投资率、人均人力资本存量和上期人均实际GDP对均衡人均GDP都存在显著正向作用，人口增长率与折旧率之和对人均均衡GDP的影响为负。

模型（3）、（4）在基准增长模型的基础上引入了反映劳动力年龄结构和劳动力市场状况的变量。固定效应和GMM估计结果中，45岁及以上老年劳动力份额对人均均衡GDP的影响均显著为负，表明劳动力老龄化已对我国经济产生了不利影响。然而，第一种劳动力年龄结构分类下的中年劳动力份额，在两种估计方法下均表现出与人均均衡GDP的负相关性，并且在GMM估计中还通过了5%的显著性检验，这与现有研究结果不符。

模型（5）和（6）采用了第二种劳动力年龄结构分类法。中年劳动力份额在固定效应估计中系数为正，GMM估计中为负，但均未通过显著性检验，表明中年劳动力年龄界限划分是合理的，35-49岁是个人劳动生产率的高峰期。系数未通过显著性检验正是我国国情的真实反映，因为劳动力年龄结构老龄化、巨大的就业压力、相对较低的劳动力素质、劳动力不得其用等诸多问题，使得中年劳动力难以成为促进人均GDP增长的因素。

两种劳动力年龄结构分类中，青年劳动力与人均均衡GDP间均为负向关系。因为青年劳动力还处于生产经验积累阶段，劳动生产率较低，青年劳动力相对较低的工资水平正是其生产率较低的市场反映。另一方面，青年劳动力消费需求较旺，是住房、汽车等耐用消费品的主要消费群体，储蓄率较低，物质资本形成能力较差，从而形成了青年劳动力份额与人均均衡GDP间的负向关系。劳动参与率在两种劳动力年龄结构分类中均未通过显著性检验，说明显性失业和隐性失业消耗了相当部分的“人口红利”，如何有效降低失业率，提高劳动生产率仍是我国劳动就业领域面临的重要课题。

（二）过渡动态效应

各省人均实际GDP增长率由已经得到的1982-2010年的各省人均实际GDP分阶段年度平均计算得到，包含了除1982年之外的其余六年的人均实际GDP增长率，初始年份设为1982年。

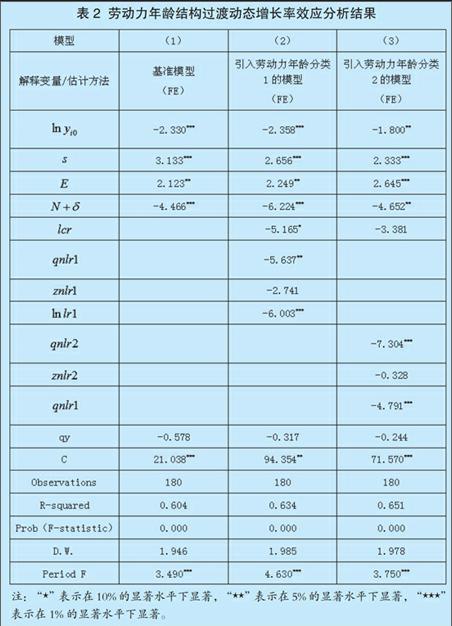
在采用固定时期还是混合模型检验中，三个计量模型的F检验结果均显示，时期固定效应模型是合理的，F统计量均达到了1%的显著水平（见表2）。基准模型（1）的回归结果与理论推导一致，物质资本投资、人均人力资本存量与实际人均GDP增长率正相关，人口和折旧率为负相关，初始人均GDP前系数为负，证实了存在条件收敛。

两种分类法下的老年劳动力份额与人均实际GDP增长率间均表现出显著负向关系，且系数都通过了1%的显著水平，说明我国劳动力老龄化程度加剧，缩小了实际人均GDP与均衡人均GDP间的距离，引起过渡动态增长率下降。

青年劳动力份额和中年劳动力份额在两种分类法下的过渡动态增长率效应方向与均衡效应中相同，证实了理论推导结果。青年劳动力份额与实际人均GDP增长率间呈负向关系;中年劳动力份额为负向关系，但未通过显著性检验。劳动参与率的过渡动态增长率效应与均衡效应中的作用方向相同，均为负，第一分类法下显著水平为10%，第二分类法下未通过显著性检验。

结论与政策建议

本文通过将劳动力年龄结构指数分别与人力资本变量和劳动力投入量相结合的方式，引入经典经济增长模型，分析了劳动力年龄结构的均衡人均产出和过渡动态增长率效应。在理论推导的基础上，收集了我国1982-2010年的省级面板数据，实证研究结果证实，劳动力老龄化对我国均衡人均产出和过渡动态增长率均存在显著不利影响。我国是在经济发展水平较低、就业压力依然巨大的情况下迎来劳动力年龄结构老龄化的，《联合国世界人口展望2015》数据显示，2035年我国45-64岁人口比重将达到30%的峰值，届时劳动力数量短缺问题将更为突出。据此，提出以下政策建议：

第一，打造富有活力的用人环境，创新用人制度，释放劳动潜能。为此，宏观层面上应千方百计保障青年劳动力就业。青年是创业、学习和积累经验的关键时期，尽管其劳动生产率较低，但给青年人以丰富、多样化的就业机会，才能在未来造就出更多具有较高生产率的劳动力，保持经济活力。企事业单位中观层面应根据经济结构调整要求，积极稳妥地推进减员增效工作，将处理过剩产能与实现有效劳动投入相结合。积极推进用人制度改革，构建科学、合理、民主的用人制度，为人才的脱颖而出打造适宜的制度环境。微观层面上应以公开、公正、公平的激励机制为核心，激发就业者的劳动潜能，实现真正意义上的科学管理。

第二，提高人口质量，实现从人口大国向人口强国的转变。人口质量的提高对增长的促进作用往往用时较长，不易察觉，但更具根本性和决定性。从中国制造向中国创造的转变，需要人才推动，经济增长方式的转变也需要储备大量合格人才。本文证实了人力资本投资对经济增长的显著正向促进作用，在劳动力数量下降不可避免的情况下，将人口数量优势转变为质量优势，是未来保持我国劳动力竞争优势的关键。

第三，推进相关制度改革，挖掘有利于经济增长的人口因素。研究证实，将45岁作为中、老年劳动力的划分界线在我国是不合适的。为此，应逐渐延长退休年龄，适应教育水平提高、人均寿命延长带来的劳动生产率高峰期年龄后移的要求，充分利用积累的宝贵人力资源。