初中物理中浮力应用的综合性问题研究

冯朝

摘 要：初中的物理知识在近几年考试中，其中的浮力、压强、密度等相关知识一直是重点，考查题目涉及知识面广，综合性强，学生在对这部分知识进行学习时也面对较大困难，特别是对浮力应用的综合性问题的掌握与分析，成为学生在学习中主要面对的学习难点。本文分析了初中物理浮力的相关概念，阐述了浮力主要应用的发展领域，并在最后对初中物理浮力应用的综合性问题进行有效研究。

关键词：初中物理 浮力应用 综合性 问题

浮力是浸在液体或者气体的物体受到一种向上的力。力的方向是竖直向上的，主要施力物体为液体或气体。产生浮力的主要原因是物体下表面所受向上的压力大于上表面所受向下的压力，表面压力差比较大，物体受到的浮力就会比较大，如果物体处在一个漂浮的状态，其中的浮力与液体对物体的向上压力就会相等。

一、初中物理浮力的阐述

浮力是物体在液体或者气体中，物体的上下表面受到的液体或气体的压力差造成的，等于物体在液体中排开的液体的重力。它的主要含义是物体浸在液体、气体中，物体受到一种竖直方向上的压力的合力，简称为浮力。物体在液体中，下表面承受到的压力大于上表面的压力，主要是因为液体中的各个表面所处的深度不同，在物体的上表面，会受到一个向下的压力；而物体的下表面，会受到一个向上的压力[1]。如果物体在同一种液体中，所处的深度越大，其中各个表面受到的压强也越大，但是压强差不变，进而压力差不变，所以受到的浮力不变。但如果一个物体漂浮，物体顶部碰不到液体，上表面不受液体压力，而在底部受到的压力，也呈现了一种压力差，从而体现物体受到的浮力等于下表面的压力的现象。

二、初中物理浮力的应用

初中的物理浮力在轮船工作的应用，主要是使一些密度大于水的建设材料能够漂浮在液体表面，并以一种空心物体的制作形式降低物体的整体密度，从而使该物体能够在水上有效航行。如果轮船是满载的运行形式，要对排开水的质量进行计算，不仅要计算出排开液体的体积，排开液体的重力，还要分析轮船受到的浮力与轮船与满载物体所受到的重力的关系。初中的物理浮力知识在潜水艇中的应用，一般潜水艇在上浮、下潜的运动过程中，都是通过改变自身重力的方式来实现的。初中物理知识在气球、飞艇方面的应用，因为气球是利用空气的浮力上升的，气球中气体的密度都小于空气的密度，特别是氢气、氦气等，所以在航空运输中飞艇的运用有很好的前景，既可以提高货物的装载量，又可以节省燃油，减少碳排放，既有经济效益，又有很好的生态和环境效益。初中物理中的浮力知识还可以应用在密度计中，因为密度计就是利用物体的悬浮特征进行设计的，一般要将密度计直立在液体中，然后按照密度计上的刻度线，从上到下的方式进行读取，其中，密度计自上而下，所对应的液体密度不断增大。

针对以上对浮力的应用分析，在对浮力知识进行计算期间，首先要确定出要研究的对象，然后对物体的受力情况的相关示意图进行研究，并分析物体在液体中的状态是静止的、还是匀速直线运动的，在分析物体受力的前提条件下，选择出合适的计算方式。

三、初中物理中浮力应用的综合性问题

1.一部分物体浸在液体中

将一部分的物体沉浸在液体中，要观察其存在的情况，主要根据一部分物体浸入液体中形成的特点进行分析，如：物体自身的向下重力与液体向上产生的浮力大小是相等，可以利用G排=F浮公式来表示。因此，如果一部分物体浸到液体中，就可以利用该公式对相关问题有效分析，以保证问题的解决更为容易。下面主要利用典型的初中物理例题对相关的问题进行分析与解决。

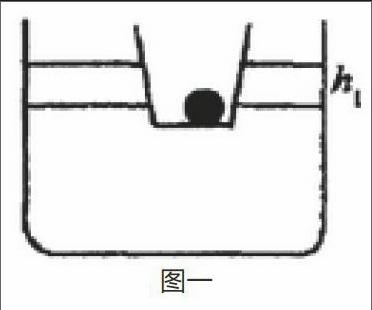
例如：根据图一中所示，在一个大烧杯中存在一些液体，其中，上面的小烧杯漂浮在大烧杯的液体表面上。在这种情况下，向小烧杯中放入一个实心的球体，这期间，大烧杯中的液体会明显升高[3]。如：图中大烧杯中的液体已经将其升高了h1，如果再将这个实心的球体从小烧杯中拿出，其中的液体高度就会下降h1，在这个实验情况下，可以分析出实心小球受到的浮力、自身的重力，排水法测出体积，进而对其中的实心球体的密度进行求解。

2.全部物体沉浸在液体中

对于全部物体沉浸到液体中所体现的类型，主要是物体向上，能够产生三个作用力的影响，其中为竖直向下的自身重力、竖直向上的液体浮力以及竖直向上的一个力[4]。其中，可以对竖直向下的自身重力设为G，竖直向上的液体浮力设为F浮，竖直向上的一个力设为T。对于竖直向上的一个力T，它既可能是吊线期间对物体产生的拉力，也可能是容器底部对物体产生的一种支持力，但如果其中的物体漂浮在液体表面，其中的竖直向上的一个力T就为零。针对以上三个作用力，可以得出三者之间的关系为G=F浮+T。对这种类型的试题进行求解，不仅要掌握整个物体浸在液体中所排开的液体体积，还要根据物体本身的受力情况进行求解。

如图二中所示，是在一个大型烧杯中盛满不同液体，然后将一个圆锥形物体放入大烧杯中，并对其中的受力情况进行观察。将圆锥形的物体重力设为G，将物体漂浮在水面上承受的向上浮力设为F，将物体悬浮在酒精中承受的浮力设为F1，然后对这两者之间的关系进行明确[5]。

对其进行具体的受力分析，在竖直方向上主要承受三个作用力：竖直向下的自身重力、竖直向下的液体的压力以及竖直向上液体的压力。其中，竖直向下的重力为G、竖直向上的液体浮力F为上下表面的压力的合力。因为圆锥在液体中呈现的状态不同，液体密度不同，排开液体的体积不同，在求解期间，可以针对以上给出的关系，分析出圆锥的自身重力不变而两次都处于平衡状态，并得出F=G，F1=G，从而F等于F1的结论。

结语

根据以上对浮力问题的分析，期间产生的综合性问题主要分为部分物体的浸入以及物体的完全浸入两种类型。针对实际问题，学生不仅需要掌握不同类型的解题特点，更需要学会运用浮力产生的原因，阿基米德原理，结合物体在液体或气体中的受力情况进行受力分析，从而能够根据问题的本质条件解决浮力问题中的综合应用问题。

参考文献：

[1] 丁丽丹.初中物理中浮力应用的综合性问题[J].课程教育研究，2015（8）：195-195.

[2] 钱云岳.浅析浮力问题的求解方法[J].中学生数理化（尝试创新版），2014（1）：31.

[3] 朱志敏.求解浮力问题的四种方法[J].中学生数理化：学研版，2012（9）：17-17.

[4] 邹远华.浮力计算题的解题规律探究[J].数理化学习，2012（8）：21-22.

[5] 叶咏.初中物理压强浮力应用的几点做法[J].考试周刊，2012（60）：136-137.