基于SAP2000单自由度体系时程分析的理论及数值研究
2016-12-05顾全军孙海涛朱彦飞陈昌宏
顾全军,孙海涛,朱彦飞,伍 妍,陈昌宏
(1.黄山睿基新能源股份有限公司,安徽245400;2.西北工业大学力学与土木建筑学院,西安710129)
基于SAP2000单自由度体系时程分析的理论及数值研究
顾全军1,孙海涛1,朱彦飞2,伍 妍2,陈昌宏2
(1.黄山睿基新能源股份有限公司,安徽245400;2.西北工业大学力学与土木建筑学院,西安710129)
本文基于SAP2000连接单元完成单自由度体系线性与非线性时程分析。根据SAP2000的粘滞阻尼单元(Damper)和Wen塑性单元(Plastic Wen)的不同属性与特点完成并列建模,快速实现单自由体系的建模与时程分析。本文以线性加速度方法总结说明了时程分析法的基本过程。此外,建模分析在文中给出了详细分析的过程且SAP2000模拟结果与理论分析结果吻合较好。
时程分析;线性;非线性;SAP2000;单自由度
引言
《高层建筑混凝土结构技术规程》(JGJ3-2010)[1~2]、《高层民用建筑钢结构技术规程》(JGJ99-2015)[3~4]等对于线性和非线性时程分析方法进行了具体的规定,涉及到线性、非线性时程分析方法适用范围,地震波的选取原则,变形验算的限值规定等方面。《建筑抗震设计规范》(GB50011-2010)[5~6]规定,对特别不规则的建筑、甲类建筑和表3.10所列高度范围的高层建筑,应采用时程分析法进行多于地震下的补充计算;当取三组加速度时程曲线输入时,计算结果宜取时程法的包络值和振型分解反应谱法的较大值;当取七组及七组以上的时程曲线时,计算结果可取时程法的平均值和振型分解反应谱法的较大值。同时,时程分析法也是规范推荐的一种弹塑性地震反应分析方法。本文基于SAP2000[7~8]提出一种单自由度体系快速建模方法,并进行线性(Linear)、非线性(Nonlinear)分析。
1 时程分析理论
地震发生时,作用在结构质点上的作用力有惯性力FI(t)、阻尼力FD(t)和恢复力FS(t)向量(如图1所示)。三者在震动过程中达到平衡,用动力方程(式(1))表示。将方程在整个震动过程中积分以便获得任意时刻结构地震反应的方法就是时程分析法,也叫做直接动力法,在数学上则称作分步积分方法。由于阻尼力与速度或位移的关系、恢复力与位移的关系可能是非弹性的,这种分析就是非弹性时程分析。如在分析时对结构物理参数引入弹塑性的假定,这种分析就是弹塑性时程分析。

图1表示单质点振动体系在地面加速度üg(t)输入下的振动位移。此时,式(1)中各项用式(2)~(4)表示:
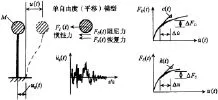
图1 单质点振动体系

式中:c(t)≈dFD(t)/du·;k(t)=dFs(t)/du;因此,式(1)可表示为:

在时间Δt内,式(5)中各地震反应参量由ui、u·i、üi变为ui+1、u·i+1、üi+1,地震动输入参量 ügi变为 ügi+1,如图2所示,各参量增量分别为△u、△u·、△ü、△üg。而阻尼系数ci、结构侧移刚度ki保持为常量,则恢复力增量fs(ui+1)-fs(ui)=ki(ui+1-ui),如图2所示。将第i时刻和第i+时刻的各参量分别代入式(5),相减后可得:
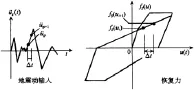
图2 地震加速度输入和恢复力
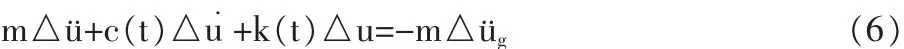
根据不同的数值积分方法,可将上式中△u·、△ü用△u表示,把式(6)化为拟静力方程:

求出△u后,与i时刻结构反应累加,便可得到第i+1时刻的位移、速度和加速度以及其他结构动力反应。将此作为下一步的初始值,根据情况调整下一加载步长内的结构阻尼、刚度参数,继续按照上述方法进行计算。如此反复,便可计算出结构在地震输入下的全部地震反应历程。通常数值积分计算通常可以使用线性加速度法、Newmark法、Wilson-θ法等。本文以线性加速度方法说明时程分析法的基本过程。
假定质点加速度在△t内按线性规律变化,相应地有加速度、位移的变化关系如图3所示。
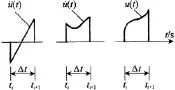
图3 线性加速度方法与速度、位移的关系
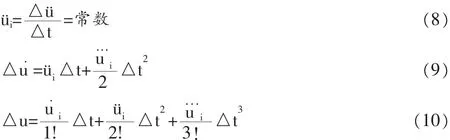
将式(8)代入式(10)得:

将式(8)代入式(19)得:

由式(11)得:

将式(13)代入式(12)得:
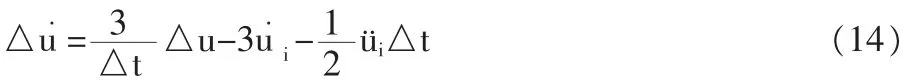
将式(13)和式(14)代入式(6),其中:
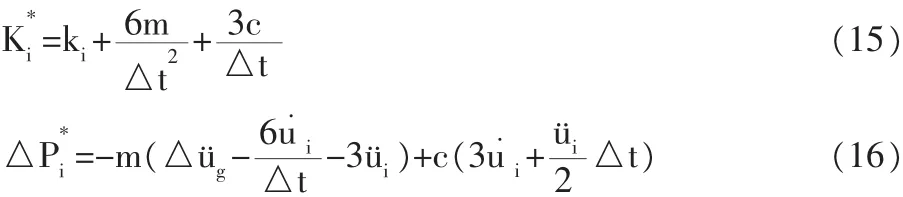
将上述用第i时刻结构反应初始值表达的参数代入式(6),求出位移增量Δu,代入式(13)和式(14),求出速度和加速度增量,将其累加后得出ti时刻的结构地震反应ü、u·、u,再将ü、u·、u作为初值,进行下一步计算。
2 SAP2000连接单元属性
在SAP2000中,一共有10种单元类型:①线性连接单元(Linear);②多段线弹性连接单元(MultiLinear Elastic);③多段线塑性连接单元(MultiLinear Plastic);④阻尼器(Damper);⑤缝(Gap);⑥钩(Hook);⑦Wen塑性单元(Plastic Wen);⑧滞回(橡胶)隔振器 (Rubber Isolator);⑨摩擦摆隔振器(Friction Isolator);⑩拉压摩擦摆隔振器(T/C Friction Isolator);本文基于SAP2000软件的Damper和Plastic Wen连接单元实现单自由度体系的时程分析。
2.1 非线性粘滞阻尼单元
粘滞阻尼单元(Damper)属性如图4所示。

图4 非线性粘滞阻尼单元属性

其中:k-弹簧常数;c-阻尼系数;exp-阻尼指数;dk-在阻尼器的变形;dc-在阻尼器的变形速度;阻尼指数必须为正数:0.2~2.0之间;弹簧和阻尼变形之和构成总内部变形:d=dk+dc若期望纯阻尼行为:弹簧的效果可通过使其有足够的刚性来得到非常小的变形。使得弹簧—阻尼器的特征时间:τ=c/k(当exp=1),为一个小于加载步大小的量(一到俩个数量级)(时间间隔)。但是:刚度不能输入的很大,否则会导致数值敏感性。
该Damper单元非线性力-变形关系:
2.2 Wen塑性单元
Wen塑性单元(PlasticWen)如图5所示,可以利用该单元快速简便模拟恢复力的滞回特性。该PlasticWen非线性力-变形关系:
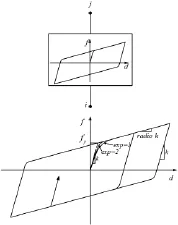
图5 Wen塑性单元属性

式中:k为弹簧常数;yield为屈服力;radio为屈服后刚度与弹性刚度k的比值;z为内部滞后变量,已知该变量范围|z|≤1;定义该单元时,需k,yield,radio,exp指数(确定屈服比率)。
3 算例分析
3.1 算例介绍
一个理想化单自由度体系如图6(a),体系总质量为200Ns2/ mm,总弹性侧移刚度为8000N/mm,黏性阻尼系数为150Ns/ mm;图6(b)为地面运动加速度,Δt=0.05s,在其作用下产生地震反应;图6(c)为假定的结构弹塑性恢复力模型,显然,屈服前结构抗侧移刚度为Py/Uy=8000N/mm,屈服后抗侧移刚度为0,卸载阶段的抗侧移刚度为8000N/mm。利用直接积分法计算结构的反应。

图6 单自由度体系非线性地震反应分析
3.2 SAP2000建模
在SAP2000中建立如图7所示模型:设置Damper单元kd=800000N/mm,cd=150Ns/mm;设置Plastic Wen单元:刚度8000N/mm,屈服力16000N,刚度比Radio=0,屈服指数exp= 20。对节点指定局部3轴的质量200Ns2/mm。为了进行线性分析对比,需对Wen单元指定线性有效刚度8000N/m。

图7 SAP2000分析模型
当然,同样可以使用“多段线塑性连接单元(Multilinear Plastic)”与“弹簧阻尼单元(Damper)”并列使用。使用Multilinear Plastic单元时,需定义如题目给出的性能骨架曲线。至于滞回类型可以选择“随动硬化(Kinematic)”或“枢纽点(Pivot)”。
3.3 分析结果
理论计算结果如表1所示,理论与数值对比结果如图8~9所示。通过修改SAP2000时程积分参数如图8、图9所示,可知α¯=0较α¯=-1/3更为准确模拟手算结果,在实际分析通常采用α¯=0。根据对比结构可知SAP2000计算与理论分析结果可知,通过SAP2000连接单元可较好实现结构的时程分析。
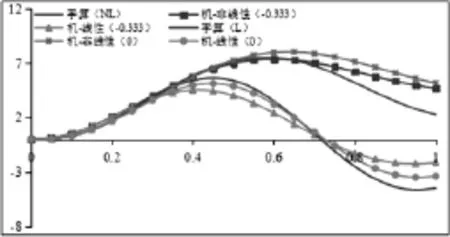
图8 数值与理论分析位移结果对比
4 结论
本文基于SAP2000连接单元完成单自由度体系线性与非线性时程分析,主要结论如下:
(1)利用Plastic Wen和Damper单元并列实现单自由度体系快速建模;
(2)通过设定合理参数,SAP2000连接单元可进行准确的时程分析;

表1 理论分析结果
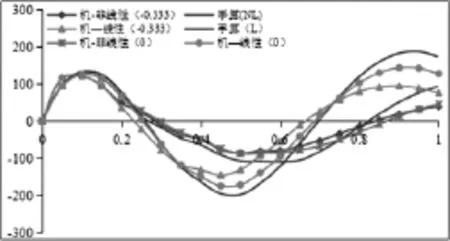
图9 数值与理论分析加速度结果对比
(3)该快速建模方法可推广至多自由度体系时程分析研究。
[1]中华人民共和国住房和城乡建设部组织.《高层民用建筑钢结构技术规程》[M].中国建筑工业出版社,2015.
[2]黄宗明,白绍良.结构地震反应时程分析中的阻尼问题评述[J].地震工程与工程振动,1996(2):95~105.
[3]中华人民共和国住房和城乡建设部组织.高层建筑混凝土结构技术规程[M].中国建筑工业出版社,2010.
[4]娄 宇,温凌燕,徐小燕,等.基于大震弹塑性时程分析的结构抗震设计[J].建筑结构,2011(5):1~8.
[5]中华人民共和国住房和城乡建设部组织.建筑抗震设计规范[M].中国建筑工业出版社,2014.
[6]曲 哲,叶列平,潘 鹏.建筑结构弹塑性时程分析中地震动记录选取方法的比较研究[J].土木工程学报,2011(7):10~21.
[7]北京金土木软件公司.SAP2000中文版使用指南[M].人民交通出版社,2011.
[8]陈昌宏.SAP2000结构工程案例分析[M].冶金工业出版社,2010.
TU352.1
A
2095-2066(2016)22-0266-03
黄山睿基新能源专项基金(2016ME060019),西北工业大学研究生创意创新种子基金重点项目(Z2016018)。
2016-7-12
顾全军(1967-),男,大专,主要从事太阳能光热光电技术研究工作。
孙海涛(1971-),男,大专,主要从事太阳能跟踪支架及控制器研发工作。
