环境温度影响下基于振动模态柔度曲率的结构损伤监测方法

黄 江 梁亚斌 冯 谦

1 中国地震局地震研究所(地震预警湖北省重点实验室)，武汉市洪山侧路40号，430071 2 武汉地震工程研究院有限公司，武汉市洪山侧路40号，430071 3 大连理工大学建设工程学部，大连市凌工路2号，116024



环境温度影响下基于振动模态柔度曲率的结构损伤监测方法

黄 江1, 2梁亚斌3冯 谦1, 2

1 中国地震局地震研究所(地震预警湖北省重点实验室)，武汉市洪山侧路40号，430071 2 武汉地震工程研究院有限公司，武汉市洪山侧路40号，430071 3 大连理工大学建设工程学部，大连市凌工路2号，116024

提出一种基于振动模态柔度曲率指数和突变指数的损伤识别方法，利用温度在结构内部连续平缓的分布特性，通过对柔度曲率进行二阶差分求导消除环境温度变化对损伤识别结果的影响，并基于协整理论给出所提方法的物理解释。最后，结合一个简支梁算例验证所提方法的有效性，利用连续监测数据对上述指标多次统计平均处理来提高抗噪性。

结构振动；模态柔度曲率；环境温度；结构健康监测

基于振动模态柔度的方法是一种重要的结构损伤识别方法[1]。Raghavendrachar等[2]通过对一个三跨钢筋混凝土桥梁的数值分析和实验，证明模态柔度比固有频率或振型对局部损伤更敏感；Zhao等[3]将固有频率和模态振型与模态柔度进行对比，也证明了模态柔度比固有频率和模态振型对损伤更敏感；Pandey 等[4]利用柔度矩阵的改变量对结构进行损伤识别，同样比固有频率或振型更敏感。然而这些方法都需要对比结构损伤前后的模态信息，不利于实际应用。唐小兵等[5]提出的模态柔度曲率方法解决了此问题，只需实测结构的模态参数便能很好地识别损伤，相较柔度矩阵对损伤更为敏感。

然而，振动模态柔度曲率较模态柔度改变量对损伤更加敏感的同时，也对诸如温度、噪声等环境因素更加敏感，计算模态柔度需要的结构频率和振型无疑都会受到环境因素和运营条件改变的影响[6]。Moorty等[7]用热弹性和参量分析比较美国多个现役桥梁温度波动影响下结构的位移与应力变化，指出温度和温度引起的边界条件改变对复合混凝土桥面的钢架桥各参数的影响较大，设计时必须加以考虑。Wood[8]对英国5座桥梁的长期振动监测表明，温度引起的桥面沥青弹性模量改变是造成结构刚度变化的主要因素。这些环境因素(尤其温度变化)对结构振动响应的影响不容忽视。

考虑到温度在几何、材料规则的结构中的传播分布是线性连续变化的特点，本文提出将结构柔度曲率进行二次求导，利用柔度曲率的曲率变化指数以及由此推导的新的损伤指标——曲率突变指数进行损伤判别，消除温度影响，并将其损伤指数进行多次统计平均来消除噪声影响。最后用一个简支梁的数值算例验证方法的可行性。

1 理论研究

1.1 模态柔度曲率(MFC)

振型对质量归一化后，可得到利用频率和振型表示的模态柔度矩阵F为[4]:

(1)

模态柔度曲率矩阵CF可表示为：

(2)

式中，Fj(i)、Fj(i-1)、Fj(i+1)分别为柔度矩阵第j列第i 、i-1、i+1行的元素;l为两单元之间的距离，当结构各单元长度相等时，l可取为1。

获得模态柔度曲率向量有两种方式:1)求每一列元素绝对值的最大值；2)取结构响应最大位置处的数据，即在此作用单位力时结构的变形最大。悬臂梁取自由端位置处、简支梁则取跨中位置处的柔度曲率向量作为某种工况下的MFC值：

MFC=max(CF)

(3)

利用模态柔度曲率MFC，即可方便地识别出结构损伤。

1.2 模态柔度指数(CI)

模态柔度曲率对损伤有很好的识别效果，但对环境温度或噪声比较敏感。柔度矩阵中每一列数值为在此列所对应的单元位置处作用单位力时整个结构的响应，由此进行插值求得的柔度曲率为整个结构在该单位力作用时响应曲线的变化率。

温度不仅影响结构的物理力学性质，还会影响结构的几何特性，进而影响结构的内力状态和空间几何形态等。但是，温度在材料均匀结构中的分布是连续而平缓的，由此产生的对结构动力特性参数的影响也是连续变化的；而结构损伤导致的构件截面面积减小和单元刚度下降却是局部的、不连续的，损伤一般只会影响受损部位构件的几何特性，其他区域则不受其影响。由此原理，可通过比较温度与损伤对结构的不同影响，分离温度变化导致的影响而识别出结构的真实损伤位置。

为提高对结构局部损伤的敏感性，提出曲率突变指数CPI作为对温度变化不敏感的结构损伤指标：

(4)

式中，CIi表示第i个模态柔度曲率指数。而模态柔度曲率指数CIMFC可通过将柔度曲率进行插值得到：

(5)

式中，MFC(i)表示第i个柔度曲率值，分别为第j列第i 、i-1、i+1行的元素。环境温度对结构各节点模态柔度的影响虽然是非线性、非平稳的，但大多具有相似趋势。因此，对模态柔度曲率进行插值计算而提出的曲率指数和模态柔度曲率突变指数相当于对结构相邻测点的柔度曲率序列进行协整变化[19]，两个或几个非平稳序列的线性组合可能成为平稳的序列。模态柔度曲率指数和曲率突变指数相当于协整余量的变化，通过式(5)的插值运算消除了温度变化对结构模态曲率的影响，和协整方法相似[ 10-11]，具有协整理论中去除环境和运行状态变化影响的效果。

1.3 曲率端点处理

二阶线性插值中端节点数值的计算，通常采用线性数值回归拟合向周边延拓的方法，即采用端节点前几个或后几个节点数据计算线性回归拟合曲线，通过拟合曲线求出端节点后一个或者前一个位置节点处的数值作为曲线延拓数值：

(6)

式中，yi表示端部外需要延拓的第i个数值，yi-1,yi-2,…,yi-m分别为用于端部延拓的前m个数据，f为近端部m个数据的拟合函数。由拟合曲线的计算过程可知，待拟合点位置离拟合所用数据点越远，拟合结果偏差越大。本文出现了式(2)、式(4)两次连续的曲率计算，为避免一次拟合过多造成数据偏差，采用分次拟合法，即用式(2)拟合一次首尾节点前后的数值，式(4)计算时再次拟合一次首尾节点前后的数值，以保证两次曲率求解后结构的节点数不致减少。

构建回归拟合曲线所用到的数据点越多，对未知点的数据拟合也就越准确。但是在损伤识别过程中，损伤的引入会导致模态曲率的波动，如果拟合所用数据中包含这些波动数据，必然会造成拟合曲线失真，从而导致数据二次污染。因此，本文简支梁算例中端节点采用相邻各节点数据的三阶线性回归拟合曲线。同时，由于端部数值的延拓仅影响到附近两个单元节点的模态曲率数值，在相关损伤指数计算完成后可将其忽略，而不影响后面的分析结果。

2 数值算例

2.1 建立简支梁的有限元模型

采用简支钢梁模型，将整梁划分为等长的40个单元，单元长度0.15m。梁为矩形截面，尺寸为0.4m×0.75m，密度为2 500kg/m3。在梁的两端施加不同的温度，梁中部单元的温度按端部温度线性插值计算，用于模拟桥梁结构日间在南北方向受到的不同温度影响。钢材弹性模量随温度的变化见图1。

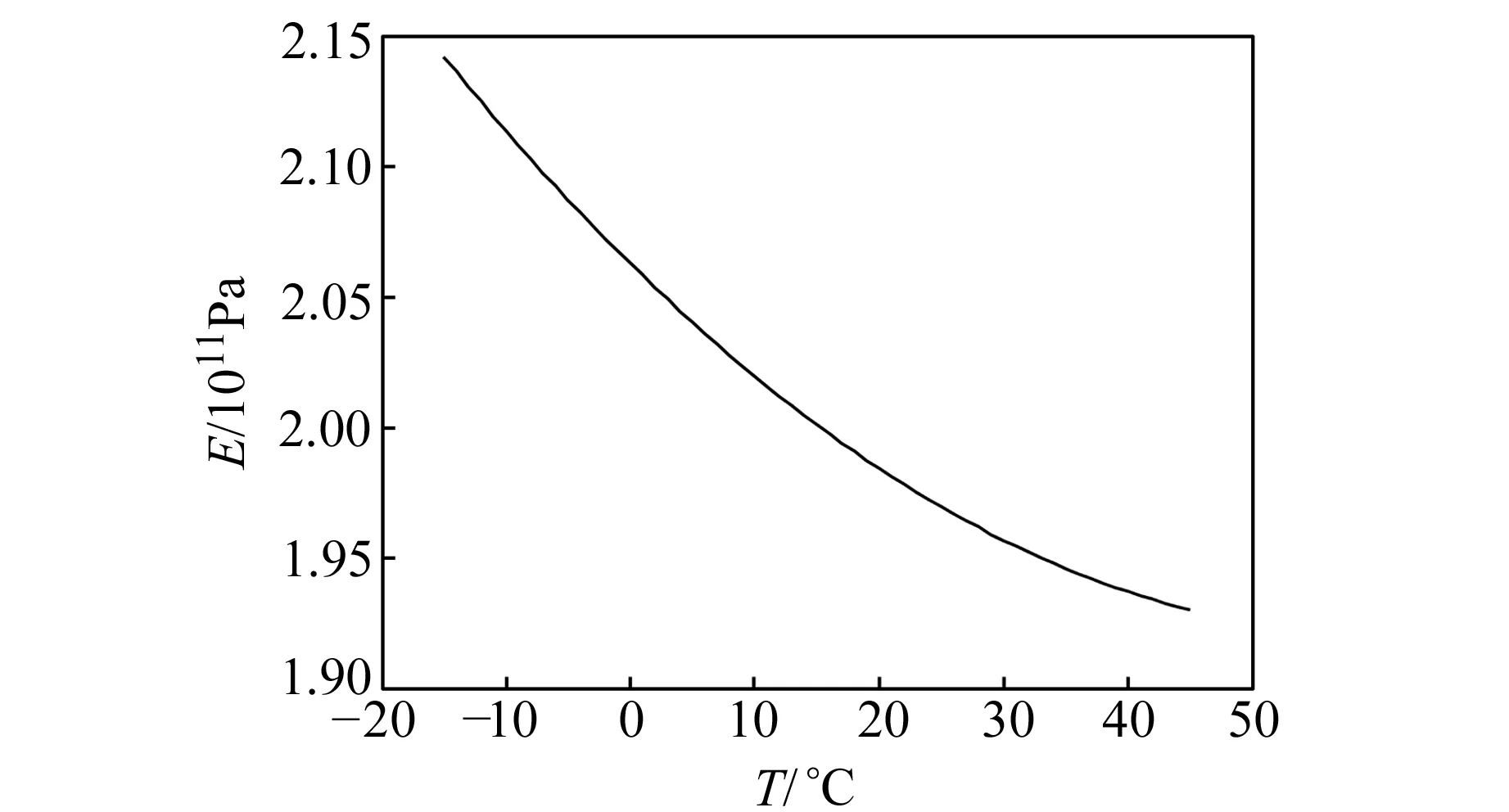
图1 钢材弹性模量随温度的变化曲线Fig.1 Young modulus of steel versus temperature

2.2 环境温度影响的去除

通过结构单元刚度的折减模拟实际结构损伤带来的刚度降低。假定单元15、单元30发生10%、15%的刚度折减，分别考察简支梁在-10 ℃(工况1)、40 ℃(工况2)、-10 ℃～10 ℃(工况3)、-10 ℃～40 ℃(工况4)4种温度工况下损伤指标的实际识别效果。其中，工况1表示简支梁整体在-10℃状态下工作；工况2表示梁左端温度为-10℃，右端温度为10 ℃，梁中各单元按线性插值计算所在处的温度；工况3和工况4分别表示不同的整体环境温度与环境温度的不同梯度。

图2(a)表示4种不同工况下温度对结构模态柔度曲率的影响。由图2(a)可知，工况4下的模态柔度曲率最小，其次是工况2和工况3，工况1模态柔度曲率最大。由图1可知，在工况4下，钢材的弹性模量最小，而模态柔度曲率与构件弹性成反比(V″(x)=-M(x)/EI)，从而使表征结构变形的结构模态柔度曲率最大；而工况1则恰好相反，结构柔度最小，柔度曲率也相应最小；工况2和工况3 的温度或者温度梯度介于工况1和工况4之间，模态柔度曲率也介于两者之间。结构

的模态柔度差可以定位结构的损伤位置，当单元15发生损伤时，与单元15相连的节点15、16在损伤前后的模态柔度差曲线上表现为最大值和次最大值，由此可认定单元15发生了损伤。在图2(a)中，模态柔度曲率受到环境温度和温度梯度的影响，同时模态柔度曲率在损伤单元15和30处的变化并不显著，单纯依靠模态柔度曲率很难判断甚至是定位结构的损伤。图2(b)表示本文提出的模态柔度曲率指数CI曲线，在4种温度工况下，除了损伤单元15、30节点附近出现细小差异外，其他地方几乎完全重合，说明本文提出的模态柔度曲率指数CI对环境温度不敏感而对损伤较为敏感，从而消除了环境温度对结构损伤识别带来的不利影响，较准确地对损伤位置进行定位。

模态柔度曲率指数CI虽然去除了环境温度的影响，但由于曲率插值的作用，使得模态柔度曲率指数在损伤单元以及损伤单元相邻位置处都出现了较大的突变值，给实际的损伤位置判别带来较大不便。本文提出的模态柔度曲率突变指数CPI则可以较好地解决这个问题。如图2(c)，在4种温度工况下，节点15、16和节点30、31都在局部达到最大值和次最大值，表明与节点15、16相连的单元15及与节点30、31相连的单元30发生损伤，清楚地指示出了损伤位置。

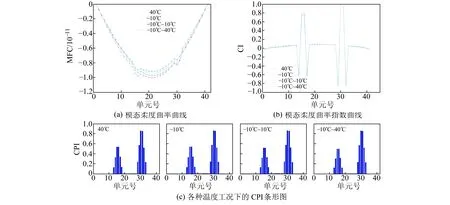
图2 4种温度工况下，单元15与单元30的损伤识别结果Fig.2 Damage detection of element 15 and 30 at four different temperature conditions

2.3 噪声影响的消除

在实际工程中，模态柔度曲率突变指数不可避免地会受到环境噪声的影响，本节研究其鲁棒性。在结构模态振型中加入5%的噪声干扰并以此来计算结构柔度矩阵，图3为所加环境噪声对模态柔度曲率和模态柔度曲率指数的影响。

由图3(a)可知，噪声对柔度曲率的影响较大。4种工况下，柔度曲率相互交织在一起，单元15、单元30处损伤引起的柔度曲率变化已经完全湮没在噪声中，柔度曲率曲线此时已不可能识别出损伤。同样，由于噪声对柔度曲率曲线的影响，导致由柔度曲线变化率推导的柔度曲率指数也无法对损伤进行判别。

为克服模态混叠对经验模态分解的影响，文献[13]提出给原始信号多次添加不同噪声再进行经验模态分解，将多次分解得到的经验模态进行总体平均以消除所加噪声的影响，从而消除模态混叠效应。本文即采用该统计平均技术提高模态柔度曲率突变指数的抗噪性。在相同噪声水平下，在模态柔度曲率中多次添加与其长度相等的白噪声，从而得到多条模态柔度曲率曲线，然后对其进行求和平均处理，以此来减弱噪声对损伤识别结果的影响。图4为对模态柔度曲率、模态柔度曲率指数和模态柔度曲率突变指数分别添加5%水平噪声后进行30次统计平均处理后的结果。

由图4可以看出，通过多次统计平均处理后，即使在5%的噪声水平下，柔度曲率指数CI以及曲率突变指数CPI均可以有效地识别出结构损伤以及定位损伤位置，表明本文方法在噪声环境下，经过统计平均处理后具有一定的鲁棒性。

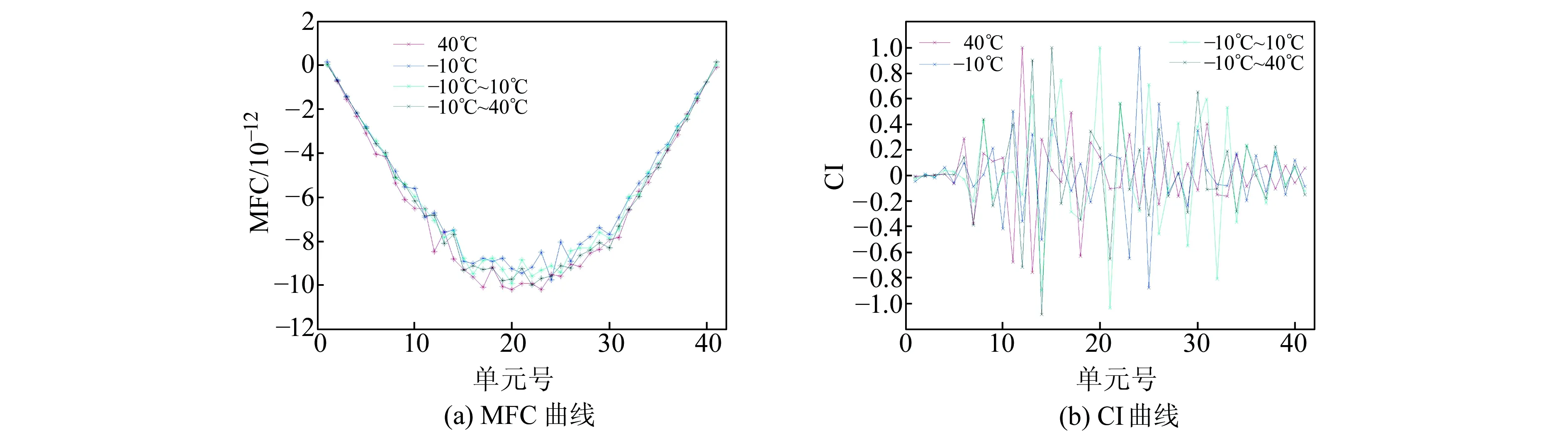
图3 5%噪声环境下4种温度工况的损伤识别结果Fig.3 Damage detection of element 15 and 30 at four different temperature conditions with 5% noise

图4 5%噪声环境下4种温度工况，30次统计平均后的单元15、单元30的损伤识别结果Fig.4 Damage detection of element 15 and 30 at four different temperature conditions with 5% noise after 30 timesstatistical averaging

3 结 语

本文根据温度在结构中的传播分布特性，提出振动模态柔度曲率指数CI以及振动模态柔度曲率突变指数CPI，以消除温度或温度梯度对柔度曲率损伤识别的影响。结合一个简支钢梁在不同温度工况下的算例，验证所提出的振动模态柔度曲率指数CI对环境温度不敏感而对损伤敏感，进而通过所提出的振动模态柔度曲率突变指数CPI可以更清晰地识别出损伤，并准确定位损伤的位置，且在较高噪声环境下通过多次统计平均的处理措施有效地降低噪声的影响，为在实际工程中的应用奠定了基础。

本文主要的创新点为：1)提出对环境温度变化不敏感的振动模态柔度曲率指数以及振动模态柔度曲率突变指数；2)基于协整理论给出了文中所提出的结构损伤识别指数对温度不敏感的物理解释。本文提出一种基于振动模态柔度曲率的损伤识别方法，可以较理想地识别出结构损伤而不受环境因素的影响，并且具有一定的噪声鲁棒性，在地震工程及结构健康监测领域展现出较广阔的应用前景。

[1]FarrarCR,WordenK.StructuralHealthMonitoring:AMachineLearningPerspective[M].NewJersey:JohnWiley&Sons, 2012

[2]RaghavendracharM,AktanAE.FlexibilitybyMultireferenceImpactTestingforBridgeDiagnostics[J].JournalofStructuralEngineering, 1992, 118(8): 2 186-2 203

[3]ZhaoJ,WolfJT.SensitivityStudyforVibrationalParametersUsedinDamageDetection[J].JournalofStructuralEngineering, 1999,125(4):410-416

[4]PandeyAK,BiswasM.DamageDetectioninStructuresUsingChangesinFlexibility[J].JournalofSoundandVibration, 1994, 169(1): 3-17

[5] 唐小兵，沈成武，陈定方. 结构损伤识别的柔度曲率法[J]. 武汉理工大学学报，2001,23(8):18-20(TangXiaobing,ShenChengwu,ChenDingfang.FelxibilityCurvatureMethodintheDamageDetectionofStructures[J].JournalofWuhanUniversityofTechnology, 2001, 23(8):18-20)

[6]SohnH.EffectsofEnvironmentalandOperationalVariabilityonStructuralHealthMonitoring[J].PhilosophicalTransactionsoftheRoyalSocietyA:Mathematical,PhysicalandEngineeringSciences, 2007, 365(1 851): 539-560

[7]MoortyS,RoederCW.Temperature-DependentBridgeMovements[J].JournalofStructuralEngineering, 1992, 118(4): 1 090-1 105

[8]WoodMG.DamageAnalysisofBridgeStructuresUsingVibrationalTechniques[D].Birmingham:UniversityofAston, 1992

[9]ZhouC,LiHN,LiDS,etal.OnlineDamageDetectionUsingPairCointegrationMethodofTime-VaryingDisplacement[J].SmartStructuresandSystems, 2013, 12(3-4): 309-325

[10]CrossEJ,WordenK,ChenQ.Cointegration:ANovelApproachfortheRemovalofEnvironmentalTrendsinStructuralHealthMonitoringData[J].ProceedingsoftheRoyalSocietyA:Mathematical,PhysicalandEngineeringSciences, 2011, 467(2 133):2 712-2 732

[11]CrossEJ,MansonG,WordenK,etal.FeaturesforDamageDetectionwithInsensitivitytoEnvironmentalandOperationalVariations[J].ProceedingsoftheRoyalSocietyA:Mathematical,PhysicalandEngineeringSciences, 2012, 468(2 148):4 098-4 122

[12]WuZH,HuangNE.EnsembleEmpiricalModeDecomposition:ANoise-AssistedDataAnalysisMethod[J].AdvancesinAdaptiveDataAnalysis,2009,1(1):1-41

[13]闵志华，孙利民，仲政. 环境温度对斜拉桥动力特性的影响分析[J]. 同济大学学报：自然科学版，2011,39(4):488-494(MinZhihua,SunLimin,ZhongZheng.EffectAnalysisofEnvironmentalTemperatureonDynamicPropertiesofCable-StayedBridge[J].JournalofTongjiUniversity:NaturalScience, 2011,39(4):488-494)

About the first author:HUANG Jiang, senior engineer, majors in earthquake engineering, engineering detecting, structural damage identification, E-mail:huangjian72024@163.com.

Damage Identification Method Research under the Influence of Environmental Temperature Based on Structural Vibration Mode Flexibility Curvature

HUANGJiang1,2LIANGYabin3FENGQian1,2

1 Hubei Key Laboratory of Earthquake Early Warning, Institute of Seismology, CEA，40 Hongshance Road, Wuhan 430071, China 2 Wuhan Institute of Earthquake Engineering Co Ltd, 40 Hongshance Road, Wuhan 430071,China 3 Faculty of Infrastructure Engineering, Dalian University of Technology, 2 Linggong Road, Dalian 116024, China

A novel detection approach using curvature index of modal flexibility curvature and its curvature damage diagnosis index is proposed in this paper. The proposed method is based on the unique character of temperature propagation and distribution in structure; the temperature disturbance can be eliminated by differentiating a second time for flexibility curvature. A physical interpretation is demonstrated for the proposed method based on cointegration theory. The validity and effectiveness of the proposed method are illustrated through a simple supported beam simulation, and a statistical averaging technique is utilized to improve the noise resistance of these damage indexes. Thus, the proposed method has the potential to be implemented in practical applications.

structural vibration; mode flexibility curvature; environmental temperature; structure healthy monitoring

National Natural Science Fundation of China, No.51608493; Innovative Research Groups Foundation of NFSC, No. 51121005.

2015-11-09

项目来源：国家自然科学基金青年科学基金(51608493);国家自然科学基金创新研究群体科学基金(51121005)。

黄江，高级工程师，研究方向为地震工程、工程检测与结构损伤识别，E-mail：huangjian72024@163.com。

10.14075/j.jgg.2016.12.020

1671-5942(2016)012-1121-05

P315

A