附不等式约束的总体最小二乘迭代算法

汪奇生 杨根新

1 湖南软件职业学院建筑工程学院，湘潭市开源路1号，411100 2 云南国土资源职业学院测绘地理信息学院，昆明市经牛路2号，650217



附不等式约束的总体最小二乘迭代算法

汪奇生1杨根新2

1 湖南软件职业学院建筑工程学院，湘潭市开源路1号，411100 2 云南国土资源职业学院测绘地理信息学院，昆明市经牛路2号，650217

基于惩罚函数和测量平差中权的思想，提出了附不等式约束的总体最小二乘平差模型，即利用惩罚函数对不等式约束方程构造约束权，通过零权和无限权将不等式约束转换为等式约束，从而将不等式约束平差准则转化为传统的测量平差准则。同时，根据非线性最小二乘平差理论，用构造结构矩阵的方法来顾及系数矩阵的结构性，推导了附不等式约束的总体最小二乘迭代算法。该算法迭代格式与传统的间接平差类似，只需经过若干次迭代便能得到最优解。

不等式约束；EIV模型；总体最小二乘；迭代算法；惩罚函数

总体最小二乘(total least squares)是一种能同时考虑系数矩阵误差的方法[1]，受到各领域学者的广泛关注。在测量数据处理中，总体最小二乘估计方法对应的平差模型为EIV(errors in variables)模型。对于EIV模型的解算，国内外学者进行了深入研究[2-9]。其中，文献[2]运用拉格朗日原理首次提出总体最小二乘的迭代法，文献[3]针对线性回归系数矩阵含有常数列提出了其总体最小二乘解，文献[4-8]研究了加权总体最小二乘算法并应用于测量数据处理。除此之外，一些学者还研究了扩展总体最小二乘的一些其他算法[9]。

以上算法都没有考虑参数估计时的先验信息。当存在某些先验信息时，可根据先验信息对参数附加某种约束。如果约束是等式，则可以构建附有等式约束的总体最小二乘模型(equality constrained EIV,ECEIV)。对于ECEIV模型的解算，文献[10-12]进行了详细论述。如果约束是不等式，则可以构建附有不等式约束的总体最小二乘模型(inequality constrained EIV,ICEIV)。对于附有不等式约束的平差问题，基于最小二乘的研究成果较多[13-18]，而基于总体最小二乘的研究则较少[19-22]。其中，文献[19]采用线性互补方法通过排列组合进行求解，首次提出了附不等式约束的总体最小二乘解算方法；文献[20]采用穷举法，将不等式约束转换为等式约束问题进行求解。这两种方法算法效率低，且仅适用于系数矩阵元素全部为随机元素的EIV 模型以及等精度、不相关观测值[21]。因此，文献[21]采用惩罚函数的方法提出一种适应于系数矩阵为任意形式的算法；文献[22]则采用线性互补方法提出一种计算效率高的迭代算法。尽管上述文献分别提出了一种附有不等式约束的总体最小二乘算法，而且算法效率从低到高，算法从仅适应于系数矩阵为一般形式到任意形式，但都存在算法复杂、计算困难的问题，而且这些算法都不是基于传统的平差方法，不利于测量人员理解。

本文根据文献[18]处理最小二乘的附不等式约束平差时的思想，基于惩罚函数处理不等式约束的方法，结合传统测量平差中权的思想，提出一种类似间接平差模型的简单迭代算法。与文献[21]采用的惩罚函数方法不同的是，本文将惩罚函数处理不等式约束问题的思想与测量平差方法相结合。该算法利用构造结构矩阵来顾及系数矩阵的结构性，能处理系数矩阵为任意形式的ICEIV模型，算法迭代格式简单易懂，易于测量人员理解和掌握。

1 附不等式约束的总体最小二乘平差模型(ICEIV)

附不等式约束的总体最小二乘平差模型(ICEIV模型)为[20]：

(1)

式中，L为m×1的观测向量，VL为m×1的观测值改正向量，A为m×n的系数矩阵，EA为m×n的系数改正矩阵，X为n×1的参数估值向量，G为k×n不等式约束方程的系数矩阵且为行满秩矩阵，W为k×1的常数向量。

EIV模型的随机模型为：

(2)

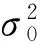
然而在实际处理时，EIV模型的系数矩阵并不是全部都含有误差，因此本文提出用结构矩阵的方法来顾及这一问题，用结构矩阵来表示系数矩阵的改正向量VA。设VA中有t×1的元素含有误差，则：

VA=DVa

(3)

式中，Va是t×1的系数矩阵中含误差的非重复元素的改正数(数量为t个)，D是mn×t的结构矩阵。因此，ICEIV平差模型可以表示为：

(4)

式中，vec-1(·)表示vec(·)的逆运算。ICEIV的随机模型为：

(5)

按照总体最小二乘原理，ICEIV模型的平差准则为：

(6)

这是一个附不等式约束的二次规划问题。根据文献[18]，按最优化理论，可以根据惩罚函数方法将上述问题转化为无约束最优化问题：

(7)

式中，P(x)为惩罚函数。式(7)的基本思想是对目标函数式(6)中不满足约束条件的点给予惩罚，即给P(x)取一个很大的值；当满足约束条件时，则P(x)取值为0，转化为无约束的普通总体最小二乘问题。在最优化计算中，惩罚函数具体形式一般凭经验确定，也可由先验信息的置信度决定。对于式(6)的不等式约束，令V0=GX-W，则可构造惩罚函数：

(8)

式中，P0称为约束权，其取值条件为：

(9)

根据式(8)、式(9)，当满足约束条件时，P0(i)=0即为无效约束；当不满足条件时，P0(i)=μ，为一个很大的数即为有效约束。通过平差中权的处理，使式(8)符合惩罚函数的特点。

由此，附不等式约束的总体最小二乘平差准则可由式(6)转化为：

(10)

通过上文分析，实际上附不等式约束的总体最小二乘平差模型可以转化为等式约束的总体最小二乘平差模型，即式(4)可以等价为：

(11)

在式(10)的平差准则下，通过迭代方法可以求得式(11)的最优解。

2 附不等式约束的总体最小二乘迭代算法(ICTLS)

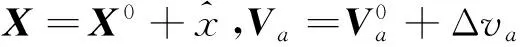
展开后化简得：

(12)

式中，⊗为矩阵的可内克积。根据总体最小二乘原理，可将式(12)写成间接平差形式：

(13)

可将上式表示为：

(14)

根据间接平差原理，上式的解为：

(15)

式(14)即为普通的最小二乘间接平差模型。要求附不等式约束的总体最小二乘解，需要通过式(15)进行迭代计算。式(13)、(14)即为迭代的基本格式。

本文的附不等式约束的总体最小二乘迭代算法的具体解算步骤为：

4)重复第3步，直到两次计算的参数之差小于给定的限差，则停止迭代，输出参数值。

3 实例分析

3.1 实例1

实例数据选自文献[13]，如表1所示。表中的数据包括系数矩阵和常数向量的值，并附有3个不等式约束，同时对xi的取值有限制。

表1 算例原始数据

在表1中，共有11个不等式约束，其中对xi的取值限制可以表示为8个不等式约束，对应的x1约束可以表示成：

(16)

根据式(16)，可以类似将x2、x2、x3的取值限制表示成不等式约束。

分别采用总体最小二乘法、文献[20]法、文献[21]法、文献[22]法以及本文的方法进行参数求解，其中采用本文方法构造的结构矩阵为单位矩阵D=eye(20)，取迭代停止条件ε=10-10。参数求解的结果如表2所示。

表2 估计结果

从表2可以发现，由于本例的系数矩阵全部含有误差，因此采用本文方法与其他3种方法得到的参数估值是完全相同的，即满足先验信息的约束条件，而总体最小二乘解则不能满足约束条件,这说明本文所述的附有不等式约束的总体最小二乘迭代算法是可行的。相比之下，本文采用的迭代算法既能弥补文献算法计算量大的缺陷，又能通过结构矩阵来顾及系数矩阵的结构性，同时算法的迭代形式简单，易于编程实现。

3.2 实例2

表3 线性回归数据

表4 估计结果

从表4可以看出，对于系数矩阵具有结构性的附不等式约束的总体最小二乘模型，本文算法求得的参数估值与文献[21]、文献[22]的结果相同，都满足约束条件，而总体最小二乘解则不满足。这再次验证了本文算法可以解算系数矩阵具有任意结构特性的附不等式约束的总体最小二乘模型。

4 结 语

本文根据最优化理论中惩罚函数方法，结合总体最小二乘平差准则提出的附有不等式约束的总体最小二乘迭代算法是可行的。该算法将不等式约束转换为约束权的形式，迭代格式与间接平差相似，算法与传统的平差方法接近，只需经过若干次迭代便可得到最优解。

本文的算法通过结构矩阵来处理系数矩阵含常数项或重复元素的情况，能较好地顾及到模型系数矩阵具有的结构特性。通过采用两个算例进行分析，说明了本文算法的正确性，同时也验证了本文算法能处理系数矩阵具有结构特性的问题。

[1] Golub G H,Vanloan C F．An Analysis of the Total Least Squares Problem[J]．SIAM Journal on Numerical Analysis,1980,17(6):883G893

[2] Schaffrin B. A Note on Constrained Total Least-Squares Estimation[J]. Linear Algebra and Its Applications, 2006, 417(1): 245-258

[3] 汪奇生，杨德宏，杨建文. 基于总体最小二乘的线性回归迭代算法[J]. 大地测量与地球动力学, 2013, 33(6): 112-114 (Wang Qisheng，Yang Dehong，Yang Jianwen. An Iteration Algorithm of Linear Regression Based on Total Least Squares[J]. Journal of Geodesy and Geodynamics，2013, 33(6): 112-114)

[4] Schaffrin B,Wieser A. On Weighted Total Least-Squares Adjustment for Linear Regression[J].Journal of Geodesy,2008,82(7): 415-421

[5] Shen Y Z,Li B F,Chen Y. An Iterative Solution of Weighted Total Least-Squares Adjustment[J]. Journal of Geodesy,2010, 85(4): 229-238

[6] Mahboub V.On Weighted Total Least-Squares for Geodetic Transformations[J].Journal of Geodesy, 2012,86(5): 359-367[7] Neitzel F. Generalization of Total Least-Squares on Example of Unweighted and Weighted 2D Similarity Transformation[J]. Journal of Geodesy, 2010, 84(12): 751-762

[8] Xu P L,Liu J N,Shi C.Total Least Squares Adjustment in Partial Errors-in-Variables Models:Algorithm and Statistical Analysis[J]. Journal of Geodesy,2012, 86(8):661-675

[9] 刘经南,曾文宪,徐培亮.整体最小二乘估计的研究进展[J].武汉大学学报:信息科学版, 2013, 38(5): 505-512(Liu Jingnan, Zeng Wenxian, Xu Peiliang. Overviwe of Total Least Squares Methods[J]. Geomatics and Information Science of WuhanUniversity,2013,38(5):505-512)

[10]Schaffrin B,Felus Y A．On Total Least Squares Adjustment with Constraints[C].International Associationof Geodesy Symposia,Sapporo,2005

[11]Mahboub V, Sharifi M A. On Weighted Total Least-Squares with Linear and Quadratic Constraints[J]. Journal of Geodesy, 2013, 87(3): 279-286

[12]Fang X. A Structured and Constrained Total Least-Squares Solution with Cross-Covariances[J]. Studia Geophysica et Geodaetica, 2013: 1-16

[13]Peng J，Guo C, Zhan H． An Aggregate Constraint Method for Inequality-Constrained Least Squares Problem[J].Journal of Geodesy，2006，79(12): 705-713

[14]Zhu J,Santerre R,Chang X W.A Bayesian Method for Linear Inequality Constrained Adjustment and Its Application to GPS Positioning[J].Journal of Geodesy,2005,78(9):528-534

[15]冯光财,朱建军.基于有效约束的附不等式约束平差的一种新算法[J].测绘学报, 2007,36(2):119-122(Feng Guangcai,Zhu Jianjun.A New Approach to Inequality Constrained Least-Squares Adjustment[J].Acta Geodaeticaet Cartographica Sinica,2007,36(2):119-122)

[16]朱建军,欧阳文森,文小岳.基于遗传算法解决附有不等式约束的最小二乘平差问题的研究[J].工程勘察,2006(3):61-64(Zhu Jianjun,Ouyang Wensen,Wen Xiaoyue.Solving the LICA Problem by GA Method [J].Journal of Geotechnical Investigation & Surveying,2006(3):61-64)

[17]宋迎春,左廷英,朱建军.带有线性不等式约束平差模型的算法研究[J].测绘学报,2008,37(4):433-437(Song Yingchun,Zuo Tingying,Zhu Jianjun.Research on Algorithm of Adjustment Model with Linear Inequality Constrained Parameters[J]. Acta Geodaeticaet Cartographica Sinica,2008,37(4):433-437)

[18]朱建军,谢建. 附不等式约束平差的一种简单迭代算法[J]. 测绘学报, 2011, 40(2): 209-211(Zhu Jianjun,Xie Jian. A Simple Iterative Algorithm for Inequality Constrained Adjustment[J]. Acta Geodaeticaet Cartographica Sinica, 2011, 40(2): 209-211)

[19]Moor B.Total Linear Least Squares with Inequality Constraints[R].Department of Electrical Engineering,Delft University,1990

[20]Zhang S L, Tong X H, Zhang K．A Solution to EIV Model with Inequality Constraints and Its Geodetic Applications[J]. Journal of Geodesy,2013, 87(1):23-28

[21]曾文宪,方兴,刘经南,姚宜斌.附有不等式约束的加权整体最小二乘算法[J]. 测绘学报,2014,43(10):1 013-1 018 (Zeng Wenxian,Fang Xing,Liu Jingnan,et al．Weighted Total Least Squares Algorithm with Inequality Constraints[J]．Acta Geodaetica et Cartographica Sinica,2014,43(10): 1 013-1 018)

[22]Zeng W X,Liu J N,Yao Y B. On Partial Errors-in-Variables Models with Inequality Constraints of Parameters and Variables[J].Journal of Geodesy，2015，89(2): 111-119

About the first author:WANG Qisheng，assistant engineer，majors in geodetic date processing,E-mail:wangqisheng0702@163.com.

1 Iteration Algorithm of Total Least Squares with Inequality Constraints

WANGQisheng1YANGGenxin2

1 Institute of Civil Engineering, Hunan Software Vocational Institute, 1 Kaiyuan Road, Xiangtan 411100, China 2 College of Geomatics and Geoinformation, Yunnan Land and Resources Vocational College, 2 Jingniu Road,Kunming 650217,China

Based on penalty function and weight of adjustment, an inequality constraints EIV (ICEIV) model is presented. The model utilizes penalty function to construct the constraint weight for the constraint equations and transforms the inequality constraint into the equality constraint by the zero or infinite weight. So, it can transform the inequality constraint adjustment criteria into the classical adjustment criteria. Therefore, a new iteration algorithm of total least squares with inequality constraints is deduced by the nonlinear least squares adjustment theory; the method uses a structured matrix to consider the repetitive elements and constant terms.

inequality constraints；errors-in-variables model；total least squares； iteration algorithm； penalty function

Scientific Research Foundation of Education Bureau of Hunan Province,No.15C0741;Scientific Research Foundation of Education Bureau of Yunnan Province,No.2016ZZX252.

2015-12-26

项目来源：湖南省教育厅科研项目(15C0741);云南省教育厅科研基金(2016ZZX252)。

汪奇生，助理工程师，主要研究方向为大地测量数据处理,Email: wangqisheng0702@163.com。

10.14075/j.jgg.2016.12.015

1671-5942(2016)012-1100-05

P207

A