几种全球加权平均温度模型的精度验证与分析

李秦政 陈 鹏 陈宪冬

1 西安科技大学测绘科学与技术学院，西安市雁塔路58号，710054



几种全球加权平均温度模型的精度验证与分析

李秦政1陈 鹏1陈宪冬1

1 西安科技大学测绘科学与技术学院，西安市雁塔路58号，710054

利用IGRA提供的全球593个无线电探空站2014年的探空资料，对Bevis 经验公式、GTm-Ⅱ和GTm-Ⅲ模型进行精度验证，对各模型随纬度、季节的变化规律进行分析研究。结果表明，在全球范围内，GTm-Ⅲ模型的总体精度(MAE=3.26 K, RMS=4.10 K)要优于另外两个模型；3种模型的精度在中低纬度地区较高，高纬度地区较低；Bevis公式和GTm-Ⅱ模型的精度在南北半球具有不对称性；各模型精度的季节性变化规律基本一致，模型的RMS在不同季节相差2～3 K。

加权平均温度；GTm-Ⅱ；GTm-Ⅲ；精度

了解水汽分布及其时空变化规律，对于天气预报以及气候演变研究具有重要意义[1-8]。GNSS气象学为获取高精度、高时空分辨率的水汽资料提供了一种新的方法。

1 GNSS水汽反演与加权平均温度

GNSS信号通过中性气体层时产生的延迟在天顶方向包括天顶静力学延迟(ZHD)和天顶湿延迟(ZWD)。ZWD乘以转换系数Π就是可降水量：

PWV=Π·ZWD

(1)

转换系数Π为：

(2)

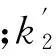
(3)

式中，ei为测站上空第i层大气平均水汽压，单位hPa；Ti为第i层大气平均温度，单位K；Δhi为第i层大气厚度，单位m。

根据误差传播定律，对式(2)进行微分，得：

(4)

式中，σΠ、σTm分别为Π、Tm的中误差。可见，大气加权平均温度与转换系数的相对误差基本相同，Tm的精度将决定转换系数的精度，并进一步影响到反演的水汽含量的精度。所以，大气加权平均温度是ZWD向PWV实时转换的关键参数。

国内外学者对大气加权平均温度进行了广泛研究。Bevis等[1]分析了美国中纬度地区13个探空站8 718份探空资料，得到适合中纬度地区的经验公式Tm= 70.2+0.72Ts(其中Ts为地表温度)。Ross等[2]通过研究全球53个探空站23 a的探空资料，得出Tm与Ts的相关性随测站地理位置以及季节的变化而变化。我国学者[5-11]也开展了大气加权平均温度区域及全球性经验模型的研究，建立了众多与地面气象因素相关的单、多因素回归模型、非气象因素全球模型。

本文利用IGRA提供的全球分布较为均匀的593个探空站2014年的探空数据，对GTm-Ⅱ、GTm-Ⅲ模型和Bevis经验公式进行验证分析。

2 GTm-Ⅱ和GTm-Ⅲ模型

Yao等[5]结合Bevis 经验公式和GPT模型[4]，并考虑到加权平均温度的年周期变化，采用全球无线电探空资料建立了适合全球的GTm-Ⅱ模型。部分学者[6-7]发现，Tm同时存在半年周期变化。因此，Yao等[6]利用2005～2011年GGOS Atmosphere 的全球Tm格网数据建立了GTm-Ⅲ模型。此模型进一步考虑到Tm的半年周期和日周期变化，且以各周期的初始相位作为模型参数。GTm-Ⅱ和GTm-Ⅲ模型表达式分别如下：

(5)

(6)

其中,

btm_mean(i)·bP(i)]

btm_amp1(i)·bP(i)]

btm_amp2(i)·bP(i)]

btm_amp3(i)·bP(i)]

式中，α1、α2分别为海平面的平均Tm值和高度改正系数，α3、α4、α5分别为与Tm年周期、半年周期、每日变化相关的系数，C1、C2、C3分别为年周期、半年周期、日变化的初始相位，hod为UTC时。

对式(5)、式(6)进行线性化，以模型系数作为待估参数。利用无线电探空的大气廓线资料结合数值积分获得全球的Tm值，或采用GGOS Atmosphere提供的全球Tm格网数据，基于最小二乘方法计算模型系数。具体过程见文献[6]。

3 模型精度的检验与分析

3.1 评定精度的指标

采用平均绝对误差(MAE)和均方根误差(RMS)作为评定Tm模型精度的指标：

(7)

(8)

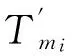
3.2 模型的年均精度检验

利用2014年探空资料结合数值积分公式计算的Tm值作为参考值，对GTm-Ⅱ、GTm-Ⅲ模型和Bevis经验公式进行年均精度验证。3种模型在全球593个测站的MAE和RMS最值与均值统计结果见表1，3种加权平均温度模型在各探空站处的精度(MAE和RMS)分布见图1。

通过表1可以看出，在全球范围内，GTm-Ⅲ模型的总体精度优于GTm-Ⅱ模型和Bevis经验公式，其MAE最大值为8.71 K，均值为3.26 K；RMS最大值为9.85 K，均值为4.10 K。由图1可知，Bevis公式的MAE小于5 K的占平均绝对误差总数的91.1%，RMS小于6 K的占均方差总数的91.2%；GTm-Ⅱ模型小于5 K的MAE占95.3%，RMS小于6 K的占92.7%；而GTm-Ⅲ模型的MAE小于5K的占93.6%，RMS小于6 K的占91.9%。因此，GTm-Ⅱ、GTm-Ⅲ模型的MAE和RMS分布集中于小误差，总体精度更高。

图1 Bevis 公式、GTm-Ⅱ、GTm-Ⅲ模型的MAE、RMS柱状图Fig.1 Histograms of MAE and RMS for Bevis formula, GTm-Ⅱ and GTm-Ⅲ models

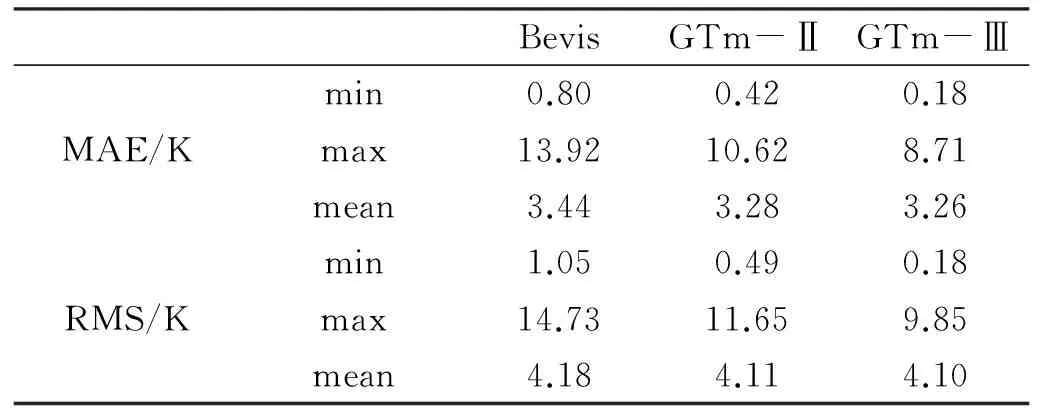
表1 Bevis、GTm-Ⅱ、GTm-Ⅲ模型的MAE和RMS统计

3.3 模型精度随纬度变化

为分析不同纬度地区各Tm模型的精度，将全球依纬度每15°划分为一个区间，从南纬90°到北纬90°依次分为12个区间。各区间加权平均温度模型统计结果见表2、表3和图2。

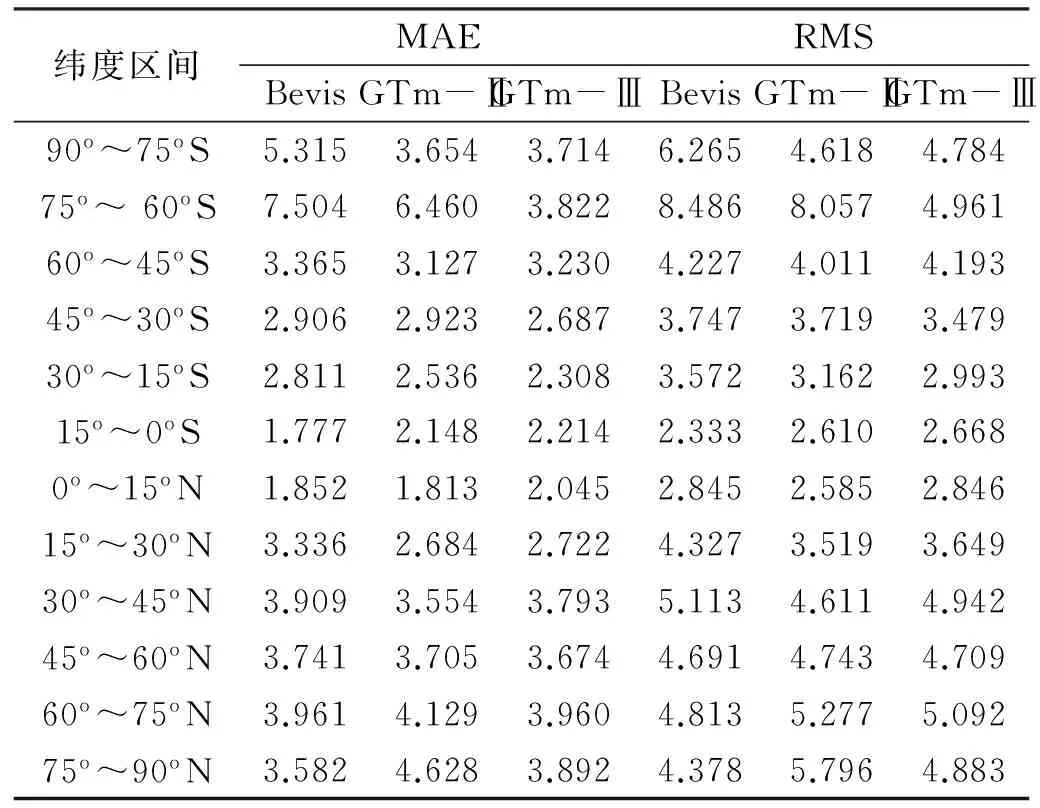
表2 不同纬度区间Bevis公式、GTm-Ⅱ和GTm-Ⅲ模型的MAE与RMS分布

表3 Bevis公式、GTm-Ⅱ、GTm-Ⅲ模型的平均绝对误差和均方根最值

由统计结果可知，3种加权平均温度模型的精度与纬度相关。模型的MAE和RMS在赤道南北15°区域内最小，在南纬60°～75°区域最大。GTm-Ⅱ模型和Bevis经验公式的精度在南北半球具有不对称性，总体是北半球的精度要优于南半球。模型精度在南北半球的不对称性与全球探空站的空间分布有关。由于设站条件限制，全球探空站大都分布在北半球的陆地区域，而在南半球浩瀚的海洋、极地区域几乎没有设站。因此，利用美国中纬度地区的探空资料回归分析建立的Bevis公式在探空数据匮乏的区域精度较低。而GTm-Ⅱ模型在建模时虽然结合了GPT模型，但由于数据源不同，同样使得模型在南半球的精度较低。

图2 不同纬度区间Bevis公式、GTm-Ⅱ、GTm-Ⅲ模型的MAE和RMS分布Fig.2 Distributions of MAE and RMS for Bevis formula,GTm-Ⅱ and GTm-Ⅲ models in different latitude ranges

各Tm模型精度随纬度的变化趋势为从南极到赤道随纬度的降低而提升，在赤道南北15°区域精度最高;从赤道区域到北极，精度有所下降，但下降幅度较前期上升的幅度小。除此之外，GTm-Ⅱ模型和Bevis公式在南纬60°～90°区域精度最差(这与陈鹏等[7]的结论一致)。

3.4 模型精度随季节变化

为了分析不同季节各Tm模型的精度分布，将2014年的探空资料按天分类统计，绘制出Tm模型的MAE、RMS时间序列图(图3)。

由图3可以看出，在全球范围内，这3种Tm模型的总体精度与季节相关，且随季节变化而变化，变化趋势较为吻合，各模型的RMS、MAE在不同季节相差2～3 K。其季节性变化规律为：夏季精度最高，冬季最低；从冬季过渡到夏季，模型精度逐渐提高；由夏季转入冬季，精度又逐渐降低。

4 结 语

本文利用IGRA提供的2014年全球593个探空站的探空数据，对GTm-Ⅱ、GTm-Ⅲ模型和Bevis公式进行精度分析。结果表明，GTm-Ⅲ模型的年均精度优于GTm-Ⅱ模型和Bevis经验公式，并且该模型的RMS、MAE误差分布更加集中；3种模型的精度与纬度相关，高纬度地区精度较低，而中低纬度地区精度较高；Bevis经验公式和GTm-Ⅱ模型的精度在南北半球具有不对称性，总体是北半球精度高于南半球；模型精度与季节相关，随季节变化的规律基本一致，各模型的RMS在不同季节相差2～3 K。由于Bevis公式是由局部探空资料回归分析得到的，并且全球GNSS测站很少配有气象观测仪器，所以Bevis经验公式应用范围相对有限。GTm-Ⅲ模型受纬度、季节变化的影响较小，在全球范围内精度较高，且不需要实测气象数据，仅需要输入测站坐标和年积日，就可以实时获得全球任意位置、高精度的加权平均温度值，因此在GNSS气象学中得到广泛应用。

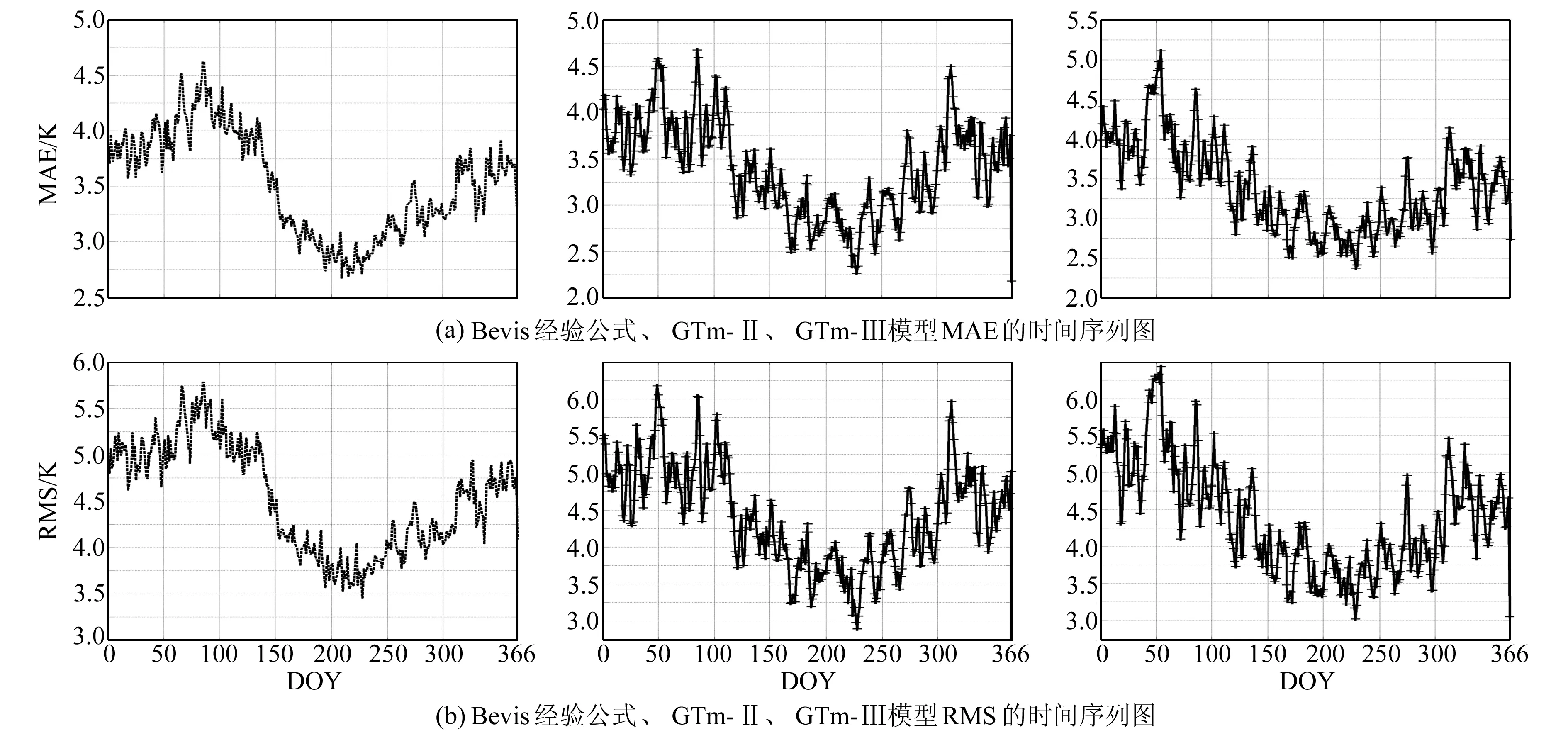
图3 Bevis经验公式、GTm-Ⅱ、GTm-Ⅲ模型MAE和RMS的时间序列图Fig.3 Time-series diagrams of MAE and RMS for Bevis formula, GTm-Ⅱ and GTm-Ⅲ models

[1] Bevis M, Businger S, Herring T A, et al. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J]. Journal of Geophysical Research, 1992, 97(D14): 15 787-15 801

[2] Ross R J, Rosenfeld S. Estimating Mean Weighted Temperature of the Atmosphere for Global Positioning System Applications[J]. Journal of Geophysical Research: Atmospheres, 1997, 102(D18): 21 719-21 730

[3] Davis J L, Herring T A, Shapiro I I, et al. Geodesy by Radio Interferometry: Effects of Atmospheric Modeling Errors on Estimates of Baseline Length[J]. Radio Science, 1985, 20(6): 1 593-1 607

[4] Böhm J, Heinkelmann R, Schuh H. Short Note: A Global Model of Pressure and Temperature for Geodetic Applications[J]. Journal of Geodesy, 2007, 81(10): 679-683

[5] Yao Y B, Zhang B, Yue S Q, et al. Global Empirical Model for Mapping Zenith Wet Delays onto Precipitable Water[J]. Journal of Geodesy, 2013, 87(5): 439-448

[6] Yao Y B, Xu C Q, Zhang B, et al. GTm-III: A New Global Empirical Model for Mapping Zenith Wet Delays onto Precipitable Water Vapour[J]. Geophysical Journal International, 2014,197(1): 202-212

[7] Chen P, Yao W Q, Zhu X J. Realization of Global Empirical Model for Mapping Zenith Wet Delays onto Precipitable Water Using NCEP Re-analysis Data[J]. Geophysical Journal International, 2014, 198(3): 1 748-1 757

[8] 谷晓平, 王长耀, 蒋国华. 地基GPS遥感大气水汽含量及在气象上的应用[J]. 气象科学, 2005, 25(5): 543-550(Gu Xiaoping, Wang Changyao, Jiang Guohua. The Research on Remote Sensing Water Vapor by Ground-Based GPS and Its Application to Weather Prediction [J]. Scientia Meteorologica Sinica, 2005, 25(5) : 543-550)

[9] 李建国, 毛节泰, 李成才, 等. 使用全球定位系统遥感水汽分布原理和中国东部地区加权 “平均温度” 的回归分析[J]. 气象学报, 1999, 57(3): 283-292( Li Jianguo, Mao Jietai, Li Chengcai, et al. The Approach to Remote Sensing of Water Vapor Based on GPS and Linear RegressionTmin Eastern Region of China [J]. Scientia Meteorologica Sinica, 1995, 57(3): 283-292)

[10]李国翠, 李国平, 杜成华, 等. 华北地区地基 GPS 水汽反演中加权平均温度模型研究[J]. 南京气象学院学报, 2009, 32(1): 80-86( Li Guocui, Li Guoping, Du Chenghua, et al. Weighted Mean Temperature Models for Mapping Zenith Wet Delay onto Precipitable Water in North China [J]. Journal of Nanjing Institute of Meteorology, 2009, 32(1): 80-86)

[11]于胜杰, 柳林涛. 水汽加权平均温度回归公式的验证与分析[J]. 武汉大学学报:信息科学版, 2009, 34(6): 741-744(Yu Shengjie, Liu Lintao. Validation and Analysis of the Water-Vapor-Weighted Mean Temperature fromTm-TsRelationship [J]. Geomatics and Information Science of Wuhan University, 2009, 34(6): 741-744)

Accuracy Validation and Analysis of Several Global Weighted Mean Temperature Models

LIQinzheng1CHENPeng1ChenXiandong1

1 College of Geomatics, Xi’an University of Science and Technology, 58 Yanta Road, Xi’an 710054, China

In this paper, the accuracy of Bevis empirical formula, GTm-Ⅱ and GTm-Ⅲ models is validated using the sounding data in year 2014 provided by integrated global radiosonde archive. Furthermore, the variation characteristics of the accuracy for these three models with latitude and season are also analyzed. Results show that the overall precision of the GTm-Ⅲ model is superior to the other two models on a global scale. The MAE and RMS values for the GTm-Ⅲ model are 3.26 and 4.10 K, respectively in global scale. It also can be found that these three models show a higher accuracy in low-middle latitude regions than at high latitude regions and that the precision of Bevis empirical formula and the GTm-Ⅱ model display a hemispherically asymmetric pattern. The seasonal variation characteristics of the accuracy for the GTm-Ⅱ, GTm-Ⅲ models and the Bevis formula present consistent variable trends and the RMS differences between four seasons are at range of 2～3 K.

weighted mean temprature; GTm-Ⅱ; GTm-Ⅲ；accuracy

National Natural Science Foundation of China, No.41404031;Open Fund of Key Laboratory of Geo-Informatics Engineering, NASMG, No.201420.

CHEN Peng, PhD, lecturer, majors in GNSS space environmental science, E-mail: chenpeng0123@gmail.com.

2016-01-05

项目来源：国家自然科学基金(41404031)；地理空间信息工程国家测绘地理信息局重点实验室开放基金(201420)。

李秦政，硕士生，主要从事GNSS气象学与GNSS多系统精密定位研究，E-mail: Lqinzheng1314@ gmail.com。

陈鹏，博士，讲师，主要从事GNSS空间环境研究，E-mail: chenpeng0123@gmail.com。

10.14075/j.jgg.2016.12.007

1671-5942(2016)012-1064-05

P228

A

About the first author:LI Qinzheng, postgraduate, majors in GNSS meteorology and multi-GNSS precise positioning, E-mail: Lqinzheng1314@gmail.com.