基于网页排名算法的敏感性分析

马莉娜，张家健，李立维

（1.河海大学 商学院，江苏 南京　210000；2.江苏省邮电规划设计院有限公司 江苏 南京210019）

基于网页排名算法的敏感性分析

马莉娜1，张家健2，李立维2

（1.河海大学 商学院，江苏 南京210000；2.江苏省邮电规划设计院有限公司 江苏 南京210019）

对网页排名算法的敏感性分析，能够进一步了解关于算法模型所给出的欢迎度评分的原理和条件范围。基于参数的不同变化会导致不同程度的敏感性这一问题，本文通过对算法的数学内容分析，研究PageRank和HITS的敏感性问题。在分析矩阵G对于比例参数α、超链接矩阵H和个性化向量vT的依赖性的基础上，分析了3个特定参数对PageRank向量的影响，最后，对HITS的敏感性进行分析。

PageRank；HITS；敏感性分析；比例参数α；超链接矩阵H；个性化向量νT

作为搜索引擎的核心部件，网页排名算法决定了搜索到的相关结果以何种顺序呈现给用户，其性能的优劣将会直接影响搜索引擎的服务质量和用户的搜索体验[1]。对网页排名算法的敏感性分析，能够进一步了解关于算法模型所给出的欢迎度评分的原理和条件范围，同样可以通过它的敏感性进一步了解网页排名算法模型的“个性”。

1　PageRank的敏感性分析

1.1α的敏感性分析

通过导数以分析α的改变对于πT的影响，πT对α求导所得的导数记为dπT（α）/dα，可知当α发生改变时，PageRank向量πT中的元素将会发生改变[2-3]。如果dπT（α）/dα中的元素j的幅值较大，当α小幅增加时，πj对于α的微小变化也会非常敏感。同时，如果dπj（α）/dα＞0，则α的小幅增加意味着Pj的PageRank将会有所提升；dπj（α）/dα＜0，则α的小幅增加意味着Pj的PageRank将会有所下降。理论角度分析，参数α的参数值在0～1之间变化，G依赖于α，进而可知G（α）=αS＋（1-α）eνT，求导dπT（α）/dα可以分析出πT（α）对α的敏感性并得出πT（α）相对于α的小幅变化的变化率。需要注意到，虽然分布πT（α）是G（α）的左特征向量，但是特征向量的元素并不一定是G（α）中元素的可微函数，因此，dπT（α）/dα的存在性需要进一步明确。设PageRank向量由下式给出：

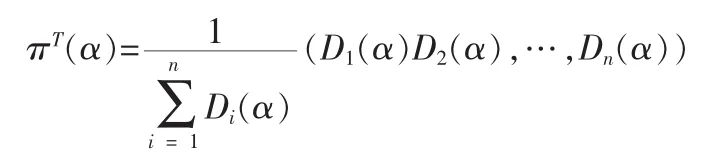
该式中，Di（α）为I-G（α）中的第i个n-1阶主子式。由于每个主子式Di（α）＞0都是I-G（α）中元素值得乘积之和，因此πT（α）中的每个元素在（0，1）区间上都是α的一个可微函数。若πT（α）=（π1（α）π2（α），…，πn（α））为PageRank向量，则对每个j=1，2，…，n，有，分析该式可知，当α值较小时，PageRank向量作为参数α的函数不会表现过于敏感，但是当α→1时，，这一上界的价值也将逐渐降低；当α值较大时，若πT（α）是矩阵G（α）=αS＋（1＋α）eνT所对应的PageRank向量，则，该导数的极限值为：（I-S）#，其中（*）#表示矩阵的群逆，所有随机矩阵的主特征值λ1=1均为半简的。因此，当S通过相似变换被简化为若当形时，所得结果为，1∉σ（C）⇒ （I-S）=X和（I-S#）=X。矩阵C由与特征值λk≠1相对应的若当块J.组成，在（I-C）-1中对应的块为（I-J.）-1。由此分析可知，当α→1时，πT（α）的敏感性由（I-S）#中元素的大小所决定。由于‖（I-S）#‖≤K（X）‖（I-C）-1‖，其中，K（X）为X的条件数，当α→1时πT（α）的敏感性主要由‖（I-C）-1‖的大小所决定，而‖（I-C）-1‖由|1-λ2|-1所决定，可知，当λ2越接近于λ1=1，则当α→1时，πT（α）就越敏感。综上分析，对于小的α值，PageRank对α的微小变动不敏感；当α值变大时，PageRank对α的微小扰动变得越来越敏感；对于接近于1的α值，PageRank对α值的微小改变非常敏感。

1.2H的敏感性分析

针对超链接矩阵H的传统算法是采用平均加权的方式以产生H矩阵的元素，即一个页面的所有出链均以随机上网者的链接概率的形式被赋予相等的权重，但是这种方法的缺点在于对随机上网者的描述方式不够准确，因为相比于随机选择一个出链页面并超链接到新的页面，上网者可能会根据许多有价值的内容或者有关的描述性锚文本来选择出链并连接到新的页面[4-5]。因此，相比于简短的广告页面，智能上网者更可能转跳到内容充实的页面，因此对这些内容更加充实的页面应该赋予更高的概率权值。可以通过将与页面中的出链位置、与出链关联的锚文本长度、由链接相连的两个文档之间的内容相似性等有关的度量加以结合的方法来填入原始超链接矩阵H中的元素，其中，利用访问日志以发现上网者的浏览习惯和喜好是填充H矩阵中元素的有效方法之一[6]，例如网络管理员通过分析上网者的访问日发现其正停留在页面P1上并且连接到P2的可能性是连接到P3的可能性的两倍。此时H矩阵中第1行的出链概率便可得到相应调整。不同的方法调整后的矩阵如下：（1）使用传统的超链接矩阵使用随机上网者方法描述：

（2）当对页面P1应用智能上网者时描述为：

但是，不管H是如何产生的，对马尔可夫链而言，关键在于所得矩阵要接近于随机矩阵，对应于非悬挂结点的行的元素之和应等于1，而对应于悬挂结点的行的元素之和应等于0[7]。如果这点不成立，那么需要对各行进行归一化处理。

针对πT对于H中的变化的敏感性，传统扰动分析指出，对于转移矩阵为P而稳态向量为πT的马尔可夫链，πT对于P中的扰动敏感|λ2（P）|≈1；对于PageRank的敏感性分析，当|λ2（G）|≤α时，对于一个可约的 S，可知 λ2（G）|=α。当α→1时，PageRank向量将对G中的变化越来越敏感，此时G与α、H和νT有关；对于单独分析超链接矩阵H的结构变化对PageRank向量的敏感性的影响，可以通过计算导数：

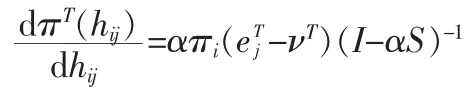
分析该式可知，当α→1时，（I-αS）-1中的元素趋向于无穷大，PageRank向量对于网络图结构中的微小变化也更为敏感。同时，与改变一个不重要的页面相比，增加一条连接或增加某个重要页面中链接的权重，对PageRank向量的敏感性也具有更大影响[8]。

1.3νT的敏感性分析

跳转矩阵E是PageRank模型最早的修改之一，使用eνT作为跳转矩阵，其中νT＞0是一个概率向量，使用νT代替1/neT意味着该跳转概率不再是均匀分布。由于νT是所有元素均为正的概率向量，因此每个结点仍然直接与其他所有结点相连，即为G素矩阵，由此可知PageRank向量是该马尔可夫链存在的唯一一个稳态向量。每当上网者发生跳转时，其将根据中所给出的概率分布跳到下一个页面，当G=αS＋（1-α）eνT时，幂法变为：

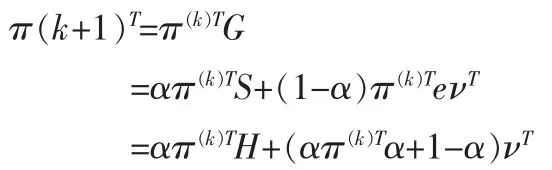
该式将每次迭代中所加的常数向量由eT/n变为νT，但是幂法的优点和结论继续保持，即渐进收敛率、稀疏向量-矩阵乘法、最小存储与易于编程等性质均得到保留。与此同时，不同个性化向量将给出不同的PageRank排名，即 πT（νT）是νT的函数[9]。但是，个性化向量νT使得与查询无关、与用户无关的PageRank变得依赖于用户，并且计算负担也增加了。

分析个性化向量νT的影响需要计算πT对νT的导数：

其中，D是悬挂结点集合，分析该式可知，πT对νT的敏感性包括：（1）该敏感性依赖于α，当α→1时，（I-αS）-1中的元素趋向于无穷大，因此，可得当α→1时，πT逐渐敏感；（2）如果悬挂结点包括PageRank中的较大部分，则PageRank向量对于个性化向量νT中的变化将更为敏感，由此可知，如果悬挂结点集较为重要，那么随机上网者将更频繁地对其进行重复访问，从而也更频繁地依照νT中给出的跳转概率以改变位置[10]。因此，随机上网者的行动以及由此得出的PageRank值的分布对于跳转向量νT中的变化具有敏感性。

2　HITS的敏感性分析

HITS利用万维网的超链接结构来生成网页的欢迎度评分，相比于PageRank，HITS给出了两个评分，且与查询相关。HITS从权威和枢纽的角度看待网页，每个页面都是某个权威的某种度量，也是某个枢纽的某种度量[11]。当HITS领域图的邻接矩阵L发生了改变并产生了新的矩阵时，分析权威向量和枢纽向量的敏感性：令E为扰动矩阵，可得=LTL+E，当λ1是一个单根时，，相比于新旧权威向量x和之间的差别的长度，更为合适的方法是考察新旧权威向量x和之间的角度，因为在HITS程序中，权威向量被归一化，同时，元素排名十分重要。两个主特征向量之间的间隔，决定了HITS的敏感性[12-13]。如果σ=λ1-λ2较大，则权威向量对于网络图中的小幅改变不敏感[14-15]；如果σ=λ1-λ2较小，则该向量可能非常敏感。

3　结束语

对网页排名算法的敏感性分析的研究已经展现其有效性，研究方法和思路更加追求创新和效率，但是无论比例参数α、超链接矩阵H和个性化向量νT对PageRank向量的敏感性分析或者HITS的敏感性分析，目前的研究都还不尽完善。由于不同算法给出的矩阵彼此之间存在明显差别，因此未来的研究工作可以将多个相互独立的算法的结果和参数的范围条件影响结果加以融合。

文献综述：

[1]杨博 等.基于超链接多样性分析的新型网页排名算法[J].计算机学报,2014（4）：883-847.

[2]Sergey Brin and Lawrence Page.The anatomy of a largescale hypertextual Web search engine.Computer Networks and ISDN Systems，1998（33）:105-118.

[3]Sergey Brin and Lawrence Page and Terry Winograd.The PageRank citation ranking:Bringing order to the Web[D]. Tech-nical Report 1999-0121，Computer Science Department，Stan-ford University，1999.

[4]Krishna Bharat and Farzin Maghoul.The term vector database:Fast access to indexing terms for webpages.Computer Networks，2010，244-257.

[5]Mattew Richardson and Petro Domingos.The intelligent surfer:Probabilisticcombinationoflinkandcontent information in PageRank.Advances in Neural Information Processing System.2012，144-148.

[6]Ricardo Baeza-Yates and Emilio Davis.Web page ranking using link attributes.In The Thirteen International World Wide Web Conference，pages 328-330，New York，2004. ACM Press.

[7]Michael W.Berry and Murray Browne.Understanding Search Engines:Mathematical Modeling and Text Retrieval.SIAM，Philadelphia，2nd edition，2005.

[8]John A.Tomlin.A new paradigm for ranking pages on the World Wide Web.In The Twelfth International World Wide Web Conference，New York 2003.ACM Press.

[9]Kristen Thorson.Modeling the Web and the computation of PageRank.Undergraduate thesis，Hollins University，2004.

[10]Sergey Brin and Bajeev Motwani.What can you do with a Web in your pocket Data Engineering Bulletin，1998：36-56.

[11]Ayman Farahat and Thomas Lofaro.Authority rankings from HITS，PageRank and SALSA:Existence，uniqueness，and effect of initialization.SIAM Journal on Scientific Computing，2006：1180-1200.

[12]Andrew Y.Ng，Alice X and Michael I.Jordan.Stable algorithms for link analysis.In Proceedings of the 24th Annual International ACM AIGIR Conference.ACM，2001.

[13]James H.Aggregation of variables in dynamic systems. Information Processing and Management，2013：111-139.

[14]Carl D.Meyer.Stochastic complementation，uncoupling Markov chains and the theory of nearly reducible systems. SIAM Review，1989：240-270.

[15]William J.Stewart.Introduction to the Numerical of Markov Chains.Princeton University Press，2004.

The sensitivity analysis based on Web page ranking algorithm

MA Li-na1，ZHANG Jia-jian2，LI Li-wei2
（1.Business School of Hohai University，Nanjing 210000，China；2.Jiangsu Posts&Telecommunication Planning and Designing Institute Co.Ltd,Nanjing 210019，China）

The sensitivity analysis of Web page ranking algorithm can achieve a further understanding on principle and condition scope of the score of welcome degree which the algorithm model given.Different changes in parameters will result in different degrees of sensitivity.Based on this problem,this article discusses the sensitivity of PageRank and HITS by mathematical content analysis of the algorithm.On the basis of analyzing the dependence of matrix G on the ratio parameter α, hyperlink matrix H and personalized vector νT,this article analyzes the influence of three specific parameters on PageRank vector.Finally,it considers the sensitivity of HITS.

PageRank；HITS；sensitivity analysis；scale parameter α；hyperlinks matrix H；personalized vector νT

TN0

A

1674－6236（2016）22-0077-03

2016-03-15稿件编号：201603173

江苏省社科联研究基金（201035）

马莉娜（1987—），女，江苏南京人，硕士。研究方向：企业管理、技术经济。