岩石细观裂隙组构的平面测定方法
2016-12-05李学丰
李学丰, 王 奇, 王 兴
(1. 宁夏大学 固体力学研究所,宁夏 银川 750021;2. 宁夏大学 物理电气信息学院,宁夏 银川 750021)
岩石细观裂隙组构的平面测定方法
李学丰1,2, 王 奇1,2, 王 兴1,2
(1. 宁夏大学 固体力学研究所,宁夏 银川 750021;2. 宁夏大学 物理电气信息学院,宁夏 银川 750021)
考虑岩石裂隙的体密度、几何尺寸和空间分布的关系,提出裂隙组构的测定新方法.该方法采用归一化的思想定义裂隙组构张量理论表达式,新的定义使得裂隙组构的零阶、二阶,四阶张量的迹均为1,极大方便了裂隙组构的试验测定.用平面裂隙张量的第二不变量定义幅值参量来描述各向异性大小,用第三不变量定义参量描述其方向,该张量的二阶、四阶形式可以用定义的参量来等价描述,参量均为标量,物理意义清晰.煤岩的CT细观试验验证表明:采用体视法原理能够很好地用于岩石细观裂隙定量测定,测试线的密度对平均裂隙率的影响较大,对裂隙平面分布的影响较小.测试线的形式对裂隙平面分布测定的影响较大,需要根据采集的图像来选用测试线的形式.二阶模拟能够很好地模拟试验的椭圆形裂隙分布规律,四阶模拟能够描述4个方向平面裂隙的分布规律.
岩石;细观裂隙组构;体视学;图像分析;煤岩CT
岩石是地壳中广泛分布的脆性材料,绝大多数具有非均质特性,形成过程中会不同程度地存在节理和缺陷,在地壳运动、外力和温度等环境作用下形成了形态复杂的裂隙.节理、缺陷和裂隙明显控制着岩石力学性质的变化,例如大量试验证实[1-3]裂隙的方向、长度、深度、高宽比和体密度明显控制着岩石破坏前、后的损伤强度、断裂变形、蠕变以及渗透等特性.对于不同尺寸裂隙的研究,形成宏观(103~10-2m)、细观(10-3~10-0m)和微观(10-2~10-6m)研究方法[2]以及结合不同尺寸的多尺度研究方法.
岩石不同尺度的裂隙描述都有2个关键要素[1]:一是裂隙体密度,即单位岩体内的裂隙数量;二是裂隙张量,即描述裂隙在岩体内的空间分布特性,分布特性和裂隙的几何尺寸及空间分布息息相关.裂隙张量描述必须考虑这2个基本要素.Kachanov[4]考虑面积因素定义了二阶裂隙组构张量的形式,后来Kanatani等[1,5-6]提出裂隙组构的广义积分形式,建议了二阶裂隙组构的定量测定方法和公式.Oda等[7-8]将裂隙理想化为圆币形,考虑它的半径和厚度建立裂隙张量的广义形式,后来用裂隙张量建立描述岩石节理的本构模型[9],通过试验观测了岩石在加载过程中裂隙的演化规律[10].张青成等[11]用CT测定了煤岩正交面上的裂隙图像,并用Kanatani[1,6]裂隙张量进行分析计算.最近,Xu等[12-13]用Oda[7-8]的裂隙张量建立岩石热力学损伤模型并应用于有限元计算.
在现有的研究成果中,裂隙描述几乎都采用了Kanatani[1,6]和Oda[7-8]两种形式,它们的特点鲜明.Kanatani的方法给出了二阶组构分量的显式公式,试验测定容易;Oda将复杂裂隙理想化后,考虑了更多的裂隙几何尺寸因素,物理意义清晰,但试验测定相对困难,因此Oda等[10]结合Kanatani[1,6]方法开展裂隙的定量分析.由此可见,在岩石裂隙的理论描述中,如果能够尽可能多地描述裂隙的几何尺寸影响,又方便试验测定,那么将会极大推动裂隙组构的理论研究、试验测定及本构模型的工程应用.
本文汲取Kanatani[1,6]方法容易试验测定和Oda[7,8]方法考虑比较多裂隙信息的优点,在笔者的岩石裂隙组构研究[14]基础上,重新定义裂隙组构的理论公式,推导平面裂隙张量的零阶、二阶和四阶表达式,用裂隙张量的不变量来描述它的空间分布规律,探索既能够尽量多地考虑裂隙的几何尺寸影响,又方便试验测定的裂隙组构描述新方法.
1 现有的岩石裂隙组构理论
岩石组成在细微观上不能视为同质体,但是宏观上一般都作为同质体来研究,内部裂隙也视为在同质体内的分布.裂隙密度、方向和大小都是在岩石同质的假设基础上分析[7-8].
1.1 密度定义和方向描述
裂隙密度ρ是单位岩体内裂隙的数量.岩体的裂隙数量可以通过裂隙的质心数来统计,裂隙密度可以等价描述为单位岩体内的裂隙质心数:

(1)
式中:mv为裂隙质心数,V为岩体体积.
裂隙由2个裂隙面组成,假定正、反面法向量分别是n和-n,2个法向量方向相反,但是裂隙密度分布函数E(n,r)满足E(n,r)=E(-n,r).为了简化,将n和-n都用n表示,则裂隙密度函数统一为E(n,r).
1.2 组构定义
Kachanov[4]定义的二阶张量αij为
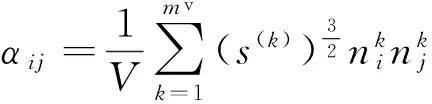
(2)
式中:s(k)为平面上第k个裂隙的面积.
Kanatani等[1,5-6]采用更容易理解的积分定义,二阶Nij和广义定义形式Nj…l分别为
Nij=∫ΩninjE(n)dΩ,
(3)
Nj…l=∫Ωninj…nlE(n)dΩ.
(4)
式中:E(n)为裂隙分布函数,Ω为积分区间.
Oda等[7,10]定义了岩石裂隙张量为

(5)
式中:Fij…l为l阶裂隙组构张量,s为裂隙面积,s=πr2;2r为裂隙直径;rm为最大裂隙半径;ni(i=1,2,3)为相对正交坐标系xi(i=1,2,3)的单位矢量;E(α,β,r)为裂隙方向密度分布函数,它是空间2个独立变化球坐标参量α、β和r的函数.
Kawamoto等[15]定义的二阶形式Ωij为
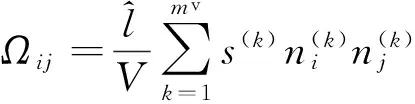
(6)

岩石裂隙合理的定量测定是广大专家学者的研究重点和难点.Kanatani等[1,6-7,10]开展了大量研究,提出不同的测定方法.Kanatani方法基于体视学原理,采用测试线的方法相对简单,因此,Oda等[10]采用的测定公式Fij…l为

(7)
式中:Nij…l为Kanatani描述的零迹张量.
以上裂隙张量定义为岩石组构理论奠定了坚实基础.从式(2)的二阶形式发展到式(4)、(5)和(7)的高阶形式,从考虑单一裂隙方向式(3)和(4)逐步到考虑更多的裂隙信息(密度、面积、裂隙半径及其方向)式(7)的形式.随着考虑信息和阶数的增加,表达式更加复杂,尽管岩石裂隙描述变得全面和详细,但复杂的表达式对它的实际应用和试验测定带来诸多不便,例如式(7)采用的方法.为此,本文在现有裂隙的研究基础上,提出新的岩石裂隙检测方法.
2 岩石裂隙张量组构的定义
在材料组构理论描述中,组构空间分布特性用一个标量和零迹张量的描述方法得到广泛认可.Kanatani[1,6]为该方法推导统一的数学框架——布冯转换.本文基于布冯转换,将岩石裂隙组构描述用标量形式描述.
2.1 广义定义
根据布冯转换公式[1,6]可知,裂隙空间分布可以用岩石平均裂隙密度和高阶零迹张量来精确描述:
E(α,β,r)=F0(1+Nijninj+Nijklninjnknl+…).
(8)
式中:E(α,β,r)为式(5)描述裂隙的分布函数,Nij和Nijkl分别为二阶和四阶零迹张量,Nij…l为l阶裂隙组构张量,l为偶数,它为无量纲的对称张量,满足Nij…l=Nji…l=Nlj…i;F0为岩石平均裂隙密度,F0用式(5)Oda零阶张量的形式:

(9)
式(5)中Ni1i2…in的一般表达式为

(10)
式中:Mij…l为l阶裂隙组构张量.裂隙组构Mij…l描述了岩石裂隙的空间高阶表达式,根据组构的大小应该为1的特点,根据式(5),采用归一化思想将Mij…l定义为

(11)
式中:Mij…l为本文定义的裂隙组构张量,Fij…l和F0分别为式(5)和(9)的定义形式.
本文岩石裂隙采用标量式(9)和高阶张量式(11)描述.标量描述了单位岩体平均裂隙数量,张量描述了裂隙面积、半径和空间几何关系的高阶分布形式.式(11)采用归一化思想描述裂隙的三维空间几何分布特点,将极大地方便裂隙组构的试验测定.
2.2 特性分析
式(11)采用归一化的思想定义,从理论上保证了张量的迹恒为一.组构为偶数阶张量,此处对零阶、二阶和四阶张量的特性进行简要分析.
式(11)的零阶张量形式为

(12)
式(11)的二阶裂隙张量为
Mij=

(13)
式中:ni和nj为坐标方向余弦值,是单位矢量,nknk≡1,因此Mkk≡1,tr(Mij)=1,即Mij的迹恒为1.裂隙分量在单位体内的积分等于其总积分.
式(11)的四阶裂隙张量为
Mijkl=

(14)
式中:ni、nj、nk和nl为单位方向余弦值.同理,容易证明tr(Mijkl)=1,即Mijkl的迹恒为1.
式(12)~(14)验证了岩石裂隙空间分布的归一化特性,张量的迹恒为1,即张量的第一不变量为1,则二阶张量可以用它的偏张量的第二、第三不变量等价描述.该特性为平面张量的试验确定和三维组构推导带来很大方便.
3 岩石平面裂隙张量的确定方法
裂隙张量描述了裂隙的几何特性在三维空间的分布特点,它是岩体内所有裂隙的几何特性的数率统计规律,高阶张量可以更精确地描述裂隙空间的不规则方向分布.本文裂隙组构的理论定义基于该特点作了最一般的定义.笔者目前无法直接试验得到裂隙的空间不规则的几何特性,但是岩体在某一方向的裂隙几何信息可以用裂隙的平面图像采集,然后利用图像处理和分析技术获取.这是现有裂隙研究广泛采用的方法,也是张量测定最基本的问题.
3.1 平面裂隙组构的确定思路
描述裂隙组构的两个关键要素是裂隙体密度和裂隙张量的确定.平面裂隙是裂隙在特定方向的投影分量,确定的关键要素为以下两个.
平面裂隙的确定思路如下:在正交坐标系下,用空间测试线扫描岩体内的裂隙分布,测定裂隙在3个方向的投影分量即为平面裂隙组构.根据该思路,平面裂隙的理论定义可以由本文建议的组构得到,然后通过试验采集3个正交面的裂隙图像,利用图像处理和分析技术获取裂隙的几何分布信息,结合组构积分定义思想可以确定平面裂隙张量的参量和裂隙密度.
如图1所示为本文裂隙的空间测定示意图.岩石内部裂隙可以通过测试线扫描测定,测试线用2个独立变量αm和βm描述,测试线在3个面的投影即为平面裂隙组构的理论值.3个正交面上的裂隙组构可以通过试验得到,如图1所示为分别从3个坐标方向采集岩体的平面裂隙图像,即x1-x3、x1-x2和x2-x3三个正交平面图像,通过图像处理和图像分析技术可得平面裂隙信息.根据试验测定值可以确定张量.

图1 描述裂隙张量坐标示意图Fig.1 Coordinate used in tvoid fabric tensor analysis
现有裂隙张量的理论和试验测定都采用分量形式,它的物理意义描述和实际应用都存在问题,不利于实际应用.为此,本文采用裂隙张量的不变量来描述.由于组构定义采用归一化思路,极大方便了平面裂隙组构的确定.下面按照裂隙确定的2个要素来详细分析.
3.2 裂隙密度
对于式(9)描述的岩石裂隙平均密度为
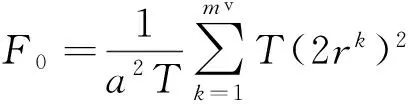
(15)
式中:a2T=V为岩体体积,a为正方形岩体边长,T为厚度;rk为第k个裂隙的半径.根据式(5)裂隙定义特点可知,裂隙面积满足sk=T(2rk).
3.3 大小和方向——二阶张量
(16)
式中:Mij为平面张量,每个的分量为4个.根据张量对称性和归一化定义,它的独立分量只有3个.用张量的不变量来定义各向异性大小和方向.
式(16)的张量可以用平面摩尔圆来描述,如图2所示,莫尔圆的半径为不变量,可以定义各向异性的大小为
(17)
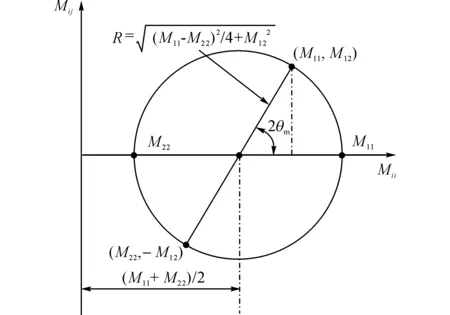
图2 裂隙张量的莫尔圆描述Fig.2 Illustration of crack tensor represented by Mohr’s circle

对于式(16)描述的平面张量在莫尔圆上的方向可以表示为
(18)

3.4 大小和方向——四阶张量
对于式(14)平面裂隙四阶张量的表达式为
(19)
式中:Mijkl为四阶张量的平面形式,它可以表示为

(20)

(21)

(22)


图3 幅值参量在裂隙主空间的几何关系Fig.3 Geometric relationship of magnitude parameter in main space of crack tensor

式(19)描述四阶张量的平面形式,可用它的不变量描述张量特性.
(23)
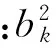
对于式(14)描述的平面张量,方向为
(24)

3.5 平面分布描述
根据式(8)描述的岩石裂隙组构的空间分布方程可知,当考虑二阶、四阶平面裂隙组构的影响时,3个正交平面的分布函数可用本文定义的不变量来等价描述为

(25)
式中:为平面坐标系描述角度,式中所有量都为标量,物理量意义清晰,都可以用细观试验直接测定.
4 岩石裂隙的体视学确定及验证
4.1 煤岩试验简介与图像
使用张青成等[11]的煤岩CT试验进行验证分析.试验设备使用工业CT系统,试样为大同煤矿的煤岩,煤岩尺寸为直径为25 mm、高50 mm的圆柱试样,制作标准为国际岩石力学学会(ISRM)推荐标准.试验对煤岩进行单轴加载,同时获取水平面、竖直3个正交面的CT图像,以便获取煤岩裂隙的三维空间分布规律.有关试验的详细介绍见文献[11].
如图4所示为试验[11]获取的煤岩在3个正交面上的CT图像,本文对该组图像作了图像处理,优化得到了二值化图像,能够清晰观测到裂隙的分布.

图4 煤岩CT二值化图像Fig.4 CT binary image of coal rock
4.2 测试线密度和测试线形状的影响
如图4(b)所示为图4(a)图像分析的结果,采用体视学原理常用的环形测试线.为了分析测试线密度对裂隙测定效果的影响,图5采用90、180和360根环形测试线对同一图像进行对比计算.可以看出:对于同种测试线,它的密度变化只对平均裂隙率有影响,对裂隙平面分布规律的测定影响不大,测试线密度越大,平均裂隙率越大,越接近于精确值.

图5 裂隙分布的图像分析结果Fig.5 Distribution of cracks with image analysis
根据4.2节的结论可知,采用的测试线密度越大,测量越接近真值.使用360根测试线,即测试线每隔0.5°进行旋转扫描.为了对比扫描测试线形状对计算结果的影响,采用不同类型几何尺寸测试线进行对比计算,使用图4(c)所示的竖直煤岩CT图像分析.

图6 图像分析采用测试线Fig.6 Test lines in image analysis
如图6(a)、(b)和(c)所示为分别采用环形、圆形和矩形测试线.环形测试线是目前体视学原理用于细观分析的常用方法,本文采用圆形和矩形两种新的测试线,可以看出矩形测试线测定裂隙的分布最全面.
如图7所示为图6几种方案的计算结果.可以看出,环形和圆形测试线测定的裂隙分布规律相似,大小不同,因环形测试线少了中心区域的测试线,裂隙率的计算值略大.矩形测试线裂隙的测定结果明显不同于环形和圆形测试线的结果,因为矩形测试线有效测定区域完全覆盖平面裂隙的分布区域,对于矩形图片,矩形测试线测定最全面.

图7 不同类型测试线的分析结果Fig.7 Results of different types of test line
4.3 试验验证分析
根据测试线密度和形状影响分析结论,采用矩形测试线对图4的3幅图片矩形图像分析,均采用360根测试线扫描裂隙分布.

综合图8可以看出:图像分析采用矩形测试线可以很好地测定裂隙的平面分布规律;二阶组构张量模拟得到椭圆形的分布规律,即可以描述裂隙的一个优势方向和一个略势方向.在该条件下,模拟值可以较好描述裂隙的最强和最弱2个方向;四阶模拟可以描述裂隙的4个方向,即最优、次优、最弱和次弱4个方向,四阶模拟能够更全面、详细地描述裂隙的分布规律.
5 结 语
考虑岩石裂隙的平均体密度、几何尺寸和空间分布关系,提出裂隙组构的测定新方法.该方法根据Oda等描述岩石裂隙的要素,采用归一化的思想重新定义裂隙组构张量理论表达式,新的定义确保裂隙组构的零阶、二阶,四阶张量的迹均为1,极大地方便了裂隙组构的试验测定.
用张量的不变量来等价描述平面裂隙组构.新定义张量的迹为1,二阶、四阶张量的偏张量的不变量独立变化量分别有2个,用第二不变量定义幅值参量来描述各向异性大小,用第三不变量定义参量描述方向,则平面张量的二阶、四阶形式可以用定义的参量来等价描述,参量均为标量,测定方便,物理几何意义清晰.
煤岩的CT试验验证表明:体视法原理能够很好地用于岩石裂隙定量测定;测试线的密度对平均裂隙率的影响较大,对裂隙平面分布的影响较小;测试线形式对裂隙平面分布规律测定的影响较大,需要根据采集的图像来选用测试线的形式;二阶模拟能够很好地模拟试验的椭圆形裂隙分布规律,四阶模拟能够描述4个方向平面裂隙的分布规律.
[1] KANATANI K I. Measurement of crack distribution in a rock mass from observation of its surfaces [J]. Soils and Foundations, 1985, 25(1): 77-83.
[2] XU H. Theoretical and numerical modeling of anisotropic damage in rock for energy geomechanics [D]. Atlanta: Georgia Institute of Technology, 2014.
[3] NARA Y. Effect of anisotropy on the long-term strength of granite [J]. Rock Mechanics and RockEngineering, 2015, 48(3): 959-969.
[4] KACHANOV M. Continuum model of medium with cracks [J]. Journal of the Engineering Mechanics Division, 1980, 106(5): 1039-1051.
[5] SATAKE M. Fundamental quantities in the graphapproach to granular materials [J]. Mechanics of Granular Materials: New Models and Constitutive Relations, 1983, 7: 9-19.
[6] KANATANI K I. Stereological determination of structural anisotropy [J]. International Journal of Engineering Science, 1984, 22(5): 531-546.
[7] ODA M. Similarity rule of crack geometry in statistically homogeneous rock masses [J]. Mechanics of Materials, 1984, 3(2): 119-129.
[8] ODA M. PERMEABILITY tensor for discontinuous rock masses [J]. Géotechnique, 1985, 35(4): 483-495.
[9] ODA M, YAMABE T, ISHIZUKA Y, et al. Elastic stress and strain in jointed rock masses by means of crack tensor analysis [J]. Rock Mechanics and RockEngineering, 1993, 26(2): 89-112.
[10] ODA M, KATSUBE T, TAKEMURA T. Microcrack evolution and brittle failure of Inada granite in triaxial compression tests at 140 MPa [J]. Journal of Geophysical Research Atmospheres, 2002, 107(10): ECV 9-1-ECV 9-17.
[11] 张青成,左建民,毛灵涛.基于体视学原理的煤岩裂隙三维表征试验研究[J].岩石力学与工程学报,2014,33(6): 1227-1232.
ZHANG Qing-cheng, ZUO Jian-min, MAO Ling-tao. Experimental study of three-dimensional characterization of coal fractures based on stereology [J] Chinese Journal of Geotechnical Engineering, 2014, 33(6): 1227-1232.
[12] XU H, ARSON C. Mechanistic analysis of rock damage anisotropy and rotation around circular cavities [J]. Rock Mechanics and Rock Engineering, 2015,52(5): 1-17.
[13] ZHU C, ARSON C. A. thermo-mechanical damage model for rock stiffness during anisotropic crack opening and closure [J]. Acta Geotechnica, 2014, 9(5): 847-867.
[14] 李学丰,王兴,袁琪.岩石裂隙组构的定量测定[J].岩石力学与工程学报,2015, 34(11): 1-7.
LI Xue-feng, WANG Xing, YUAN Qi. Quantitative determination of rock crack fabric [J]. Chinese Journal of Geotechnical Engineering, 2015, 34(11): 1-7.
[15] KAWAMOTO T, ICHIKAWA Y, KYOYA T.Deformation and fracturing behaviour of discontinuous rock mass and damage mechanics theory [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1988, 12(1): 1-30.
Determination of mesoscopic crack fabric for rock on plan
LI Xue-feng1, 2, WANG Qi1,2, WANG Xing1,2
(1.SolidMechanicsInstitute,NingxiaUniversity,Yinchuan750021,China;2.SchoolofPhysicsandElectricalInformation,NingxiaUniversity,Yinchuan750021,China)
A novel method for determination of crack fabric in rocks was proposed by considering the density, geometry and spatial distribution of cracks. The theory expression of crack tensor redefined with normalized ideas, and the trace of redefined tensor with zero-order, second-order and fourth-order is a constant, which brings a great convenience for determining crack fabric. The amplitude parameters were defined by the second variable of fabric tensor to describe the size of anisotropy, and the direction parameters were defined by the third variable to describe the direction of anisotropy. Both the second-order form and the fourth-order form of plane fabric tensor have an equivalent description with the defined parameters which are scalars with a clear physical meaning. The verification with CT tests of coal show that the method based on the principle of stereology is suitable for quantitative determination of meso cracks in rock. The density of test line has greater effect on the average crack rate and has less impact on the crack distribution. The form of test line has a greater impact on the determination of crack distribution, so it is necessary to choose the form of test lines based on test images. The simulation with second-order tensor can describe the elliptical distribution of cracks, and the simulation with fourth-order tensor can describe the four directions distribution of the plane cracks.
rock; mesoscopic crack fabric; stereology; image analysis; CT test of coal
2015-08-18.
国家自然科学基金资助项目(5168050,51669027);宁夏自然科学基金重点资助项目(NZ13001);宁夏科技支撑计划资助项目(2013年).
李学丰(1976—),男,副教授,博士,从事岩土本构模型应用及环境岩土工程的研究.ORCID:0000-0002-4533-793X.
E-mail:lixuefeng1928@163.com
10.3785/j.issn.1008-973X.2016.10.027
O 319
A
1008-973X(2016)10-2037-08
浙江大学学报(工学版)网址: www.zjujournals.com/eng
