基于改进VIKOR法的进度计划方案选择问题研究
2016-12-05王仁超曹婷婷
王仁超, 邓 剑, 曹婷婷
(天津大学 水利工程仿真与安全国家重点实验室,天津 300072)
基于改进VIKOR法的进度计划方案选择问题研究
王仁超, 邓 剑, 曹婷婷
(天津大学 水利工程仿真与安全国家重点实验室,天津 300072)
针对网络进度计划优化方案多准则群决策问题中专家对评价准则存在偏好的问题,提出基于二元语义信息的VIKOR群决策方法.该方法应用语言变量对各准则进行定性评价,使用二元语义信息对专家对准则的评价进行集结.综合考虑决策者对准则的主观偏好以及评价准则的客观权重来确定综合权重,使准则权重的确定更加合理.结合VIKOR方法,对网络进度计划优化方案进行排序,获得妥协的优化方案;通过工程案例进行计算分析,证明了该方法的实用性和可行性.
网络进度计划;多准则群决策;主观偏好;二元语义信息;VIKOR法
工程项目管理涉及工期、质量、费用以及资源均衡等多个方面,能够同时达到工期短、质量高、费用少、资源平衡是项目管理者的理想目标.这些目标之间是相互影响和相互制约的,在优化其中一个目标时将会不可避免地影响其他目标.如何择优是网络进度计划优化中需要解决的重要问题.网络计划优化方案选择是一个典型的多准则决策问题(multi-criteria decision making,MCDM),需要在决策过程中考虑多个因素.网络计划优化方案选择的实质是将备选方案排序择优的过程.在方案决策方面,目前大多数研究集中在模糊集理论[1]、数学规划法[2]、层次分析法[3]、理想点法[4]以及这些方法的结合等.事实上,在整个决策过程中,备选方案中往往不存在一个完美满足所有评价准则的最优方案,这样需要在备选方案中选择一个妥协解最优的方案.VIKOR方法是一种基于理想点的多属性决策方法,由于该方法在获得妥协解以及处理数据间的不可公度性中具有很大的优势,目前已被广泛应用于如供应商选择[5-6]以及项目选择等[7]多准则决策问题.在网络进度计划多准则决策问题中,评价准则的权重对决策结果起着关键作用,合理的确定准则权重是至关重要的.目前,国内外学者已对多准则决策问题中权重的确定这一问题进行研究,其中包括专家调查法、层次分析法、熵权法等[8-10],Chen等[11]提出基于直觉模糊熵的方法来确定评价准则的客观权重.Cook等[12]提出可以反映决策者主观权重与客观权重的综合赋权法.周荣喜等[13]以决策者对同一属性的评价值为基础,提出基于稳定性与主观性的综合熵权法.
在网络进度计划多准则决策问题中,往往需要考虑来自于业主、承包商、建设管理部门等方面的要求,并且涉及到工程工期、费用、资源供应以及工程质量等多种因素,需要进行多准则环境下的优化方案群决策.在工程实践中,由于评审专家来自于业主、承包商等不同的专业背景,对不同的评价准则有着不同的偏好,使评价结果带有一定的主观性.传统的VIKOR方法没有将决策者对评价准则的偏好考虑在内,在多准则群决策问题中,如何将专家意见进行集结是关键.二元语义信息以及相应的集结算子在综合各种偏好信息以及保持信息的完整性、真实性方面有很大的优势,可以得到更加符合决策者意愿的结果.本文通过综合考虑评价准则的主观权重和客观权重,提出基于二元语义信息的网络进度计划优化方案群决策的VIKOR法,将VIKOR方法扩展到不确定语言环境中.采用该方法不仅使得评价准则权重的确定更加合理,而且可以帮助项目管理者在多个项目进度计划方案的多准则决策中得到最优方案.
1 二元语义及VIKOR方法
1.1 二元语义信息相关概念
二元语义值模型最初由Herrera等[14]提出,通过二元语义来评价信息可以很好地避免评价信息聚合以及运算中出现的信息丢失现象,使计算结果更加合理.现有如下定义.
定义1 设S={s0,s1,…,sg}为语言评价值的集合,β∈[0,g]代表S的聚合运算结果,则β可以通过如下函数Δ表示为二元语义信息:

(1)

(2)
式中:round为四舍五入的取整算子.
定义2 设S={s0,s1,…,sg}为语言评价值集合,(si,α)是一个二元语义,则存在一个逆函数Δ-1,可以将二元语义变量转换成相应的数值β∈[0,g]:
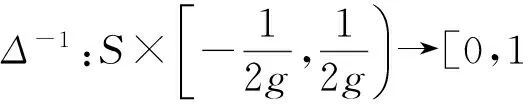
(3)
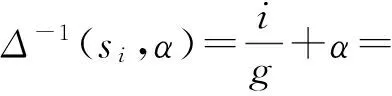
(4)
定义3 设(sk,αk)和(sl,αl)为2个二元语义,则它们之间的比较有如下规定.
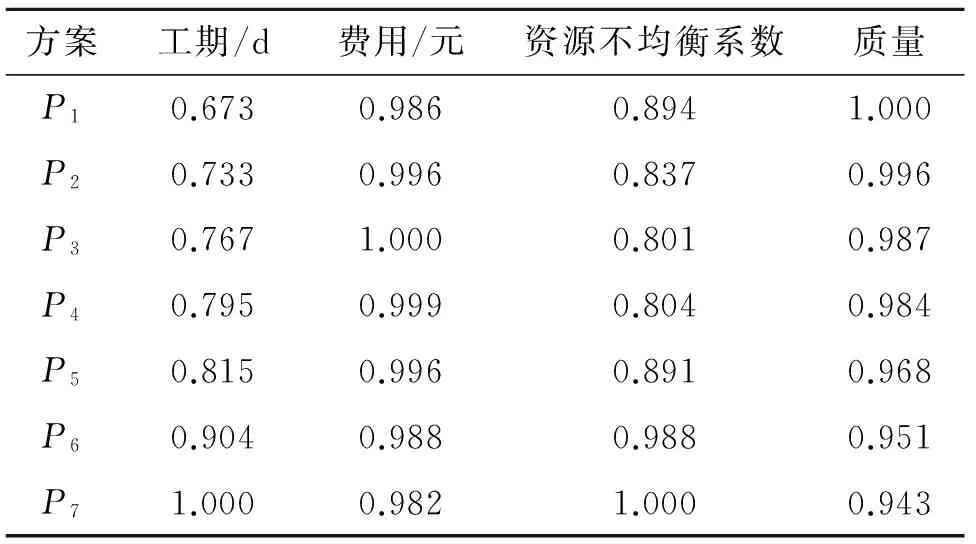
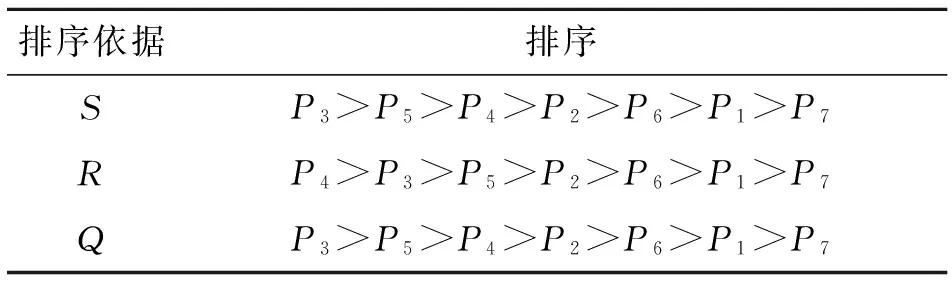
1)如果k 2)如果k TWA(X)= (5) 定义5 设(sk,αk)和(sl,αl)为2个二元语义,它们之间的距离d可以通过下式计算: (6) 1.2 VIKOR方法 VIKOR(Vlsekriterijumska Optimizacija I Kompro-misno Resenje)方法是Opricovic等[15-16]提出的一种复杂系统多准则优化决策的方法.目前已被广泛应用于如供应商选择[17]、项目选择等[18-19]多准则决策问题(MCDM).VIKOR的基本原理是先需要确定正理想解和负理想解,然后依据备选方案中每个方案与理想方案的接近程度来对备选方案进行优劣排序,其中正理想解是所有方案在各个准则下的最大值,负理想解是所有方案在各个准则下的最小值.VIKOR与TOPSIS不同的地方在于VIKOR可以根据各方案与理想解的接近程度来将方案进行排序,弥补了理想点法没有考虑备选方案距离正负理想解重要性的不足[20]. 根据文献[21]可知,妥协排序的多准则衡量由Lp-metric函数演化而来,J个不同的方案用A1,A2,…,Aj表示,方案Aj在第i个准则下的评价值为fij,Lp-metric发展而来的VIKOR方法可以表示为 1≤p≤∞, i=1,2,…,m. (7) 式中:n为决策准则的个数,Lp,j为方案Ai与理想解的距离.VIKOR方法可以同时考虑群体效用的最大化和个体遗憾的最小化,还可以反映决策者的主观偏好,得到决策者可接受的妥协解. (8) 2)计算Si、Ri: (9) 式中:Si为各优化方案的群体效益,Si越小,表示群体效益越大;Ri为个体遗憾,Ri越小,表示个体遗憾越小. 二是组织了农村水利标准制定修订、技术培训及水利普查收尾工作。为适应农村水利改革发展新变化新要求,中心面向基层水利行业培训项目管理和工程技术人员2 043名。完成了25项国家标准或行业标准的制定修订工作,编写了2014—2016年农村水利技术标准规划大纲,完成了标准项目建议书。同时,还完成了第一次全国水利普查农村供水工程、灌区专项和塘坝窖池工程普查成果自验、终验和相关资料的归档工作。 3)计算折衷值: Qj=v(Si-S*)/(S--S*)+(1-v)(Ri-R*)/ (R--R*). (10) 式中:S*=miniSi,S-=maxiSi,R*=miniRi,R-=maxiRi,v为群效用最大策略的权重,1-v为个体遗憾的权重.本研究中v取0.5,在实际中,当v>0.5时表示依据最大化群体效用的机制进行决策;当v<0.5时表示依据最小化个体遗憾的机制进行决策.本文将v设为0.5,表示同时追求群体效用的最大化及个体遗憾的最小化. 4)根据VIKOR法的思想,将备选方案按照S、R和Q的值,从小到大进行排序. 5)获得最优方案.按Q从小到大排序,第一位的备选方案A1满足以下2个条件时,即为最优方案. C1.优势可接受:Q(A2)-Q(A1)≥DQ,其中A2是按照Q值排列第二的方案,DQ=1/(m-1). 网络进度计划优化方案决策可以看作是一个多准则群决策问题,由于决策专家来自于不同的专业背景,出于建设工期、自身利益以及资源等方面考虑,对决策方案中评价准则有着不同的偏好,导致对评价准则权重的确定存在一定的主观性.评价准则权重的确定需要依据客观的事实和相应理论,才能具有较强的说服力. 在优化方案决策中难以同时满足效益型准则(如工程质量)与成本型准则(如费用、工期).例如,要想加快工程建设速度,缩短建设工期,必然要付出增加费用和影响工程质量的代价,并使得资源不均衡;要想使工程质量达到最好,就会增加费用并延长工期.本文提出基于二元语义信息的VIKOR法,进行网络进度计划优化方案的决策,具体步骤如下. 1)建立评价准则决策矩阵.决策者对各个决策准则进行语义评价,然后通过语义变量将语义评价值转换为二元语义变量.其中语义变量如下所述: {f0=VeryPoor(VP),f1=Poor(P),f2=MediumPoor(MP),f3=Medium(M),b4=Medium(M),b5=Good(G),b6=VeryGood(VG)}. 2)计算评价准则权重.首先通过TWA集结算子[14]将决策专家对决策准则的评价意见进行集结,得到各评价准则二元语义综合权重(wj,αwj). (11) (12) (13) 式中: 3)规范化数据信息.考虑到各优化方案中的各类数据具有不同的量纲,需要对各类数据进行无量纲化处理,具体计算过程如下. (14) 式中:I1属于效益型准则,I1越高越好,包括网络进度计划中的工程质量;I2属于成本型准则,I2越低越好,包括网络进度计划中的工期、费用、资源不均衡系数. 4)确定决策准则下各方案的正理想解、负理想解. 5)排序择优.计算S、R及Q,将其按照从小到大升序排列,然后通过VIKOR法的判断条件,确定最优方案. 某工程项目现有7个网络进度计划优化方案P1~P7[23],各个方案的参数如表1所示,包括各个方案的工期、费用、资源不均衡系数和工程质量.从表1可以发现,工期的压缩造成费用的增加以及工程质量的下降;若要使资源趋于均衡,则需要增大费用,同时会影响工程的质量.本文确定3个决策者DM1、DM2、DM3组决策群体进行优化方案优选的决策,专家权重分别为0.4、0.3、0.3,使用提出的决策方法,进行各个优化方案决策的计算分析. 1)决策者对评价准则进行评价,结果见表2.将表2中决策者针对各评价准则的主观语义评价转换成二元语义评价信息,转换结果如表3所示. 表1 进度计划优化方案列表 表2 专家对评价准则重要性评价 表3 准则权重的二元语义表示方式 2)通过式(12)、(13)分别求得各评价准则的主观权重、客观权重.本文将主观性系数取0.6,表示更加注重准则的主观权重,得到各准则综合权重如表4所示. 表4 各评价准则的主观、客观以及综合权重值 Tab.4 Criteria weighting by the combination weightingmethods 准则wsjwojwcjC10.2370.2400.238C20.2720.3010.284C30.1540.1130.138C40.3370.3460.341 3)通过式(14)将表1的数据进行无量纲处理,处理结果如表5所示. 表5 各方案属性值无量纲化处理结果 表6 各方案的正理想解与负理想解数值 5)计算所有方案的群体效益S、个体遗憾R及折衷值Q,如表7所示.将S、R和Q的值从小到大升序排列,结果如表8所示. 表7 备选方案的S、R以及Q计算结果 表8 备选方案按S、R以及Q值升序排列结果 从表8可以看出,备选方案P3是按照Q排序中的最佳方案,并且同时满足C1和C2这两个判定条件,即Q(P5)-Q(P3)≥1/(7-1),并且按S升序排列中P3为最优.备选方案P3为最优的方案. 本文针对网络进度计划优化方案群决策问题中决策者对决策准则存在主观偏好的问题,提出扩展VIKOR的多准则群决策方法.该方法通过语言变量对各准则进行定性评价,使用二元语义信息对决策者对准则的评价进行集结,有效地避免了信息的扭曲和丢失.针对决策者对评价准则评价过程中存在的主观偏好问题,给出综合考虑评价准则主观权重以及客观权重的综合权重确定方法和步骤.在方案排序过程中,将评价准则的综合权重运用到VIKOR方法中,通过备选方案中每个方案与理想方案的接近程度来对备选方案进行优劣排序,实现了网络进度计划方案的多准则决策,提高了优选的合理性.通过一个工程案例进行分析计算,结果表明,应用提出的方法可以在一系列的优化方案中选出符合决策者意愿的优化方案,证明了该方法的实用性和可行性,也为实际工程中其他的多准则决策问题提供了一种新的更加科学的决策方法. [1] 王坚强.信息不完全的Fuzzy群体多准则决策的规划方法[J].系统工程与电子技术,2004, 26(11): 1604-1608. WANG Jian-qiang. Programming method of fuzzy group multiple criteria decision making with incomplete information [J]. Journal of Systems Engineering and Electronics, 2004, 26(11): 1604-1608. [2] WU T, DAN L S, BLACKHURST J, et al. AIDEA: a methodology for supplier evaluation and selection in a supplier-based manufacturing environment [J]. International Journal of Manufacturing Technology and Management, 2007, 11(2): 174-192. [3] 吴冲,李汉铃.模糊AHP决策方法[J].管理工程学报,2001,15(1): 63-64. WU Chong, LI Han-ling. The decision method of fuzzy AHP [J]. Journal of Industrial Engineering and Engineering Management, 2001, 15(1): 63-64. [4] DENG Y. Plant location selection based on fuzzy TOPSIS [J]. International Journal of Advanced Manufacturing Technology, 2006, 28(7/8): 839-844. [5] SANAYEI A, MOUSAVI S F, YAZDANKHAH A. Group decision making process for supplier selection with VIKOR under fuzzy environment [J]. Expert Systems with Applications, 2010, 37(1): 24-30. [6] 阮连法,陈佳玲.基于模糊VIKOR方法的绿色建筑供应商选择[J].统计与决策,2011(21): 62-65. RUAN Lian-fa, CHEN Jia-ling. Green building supplier selection based on fuzzy VIKOR method [J]. Statistics and Decision, 2011(21): 62-65. [7] SALEHI K. A hybrid fuzzy MCDM approach for project selection problem [J]. Decision Science Letters, 2015,4(1): 109-116. [8] 田军,张朋柱,王刊良,等.基于德尔菲法的专家意见集成模型研究[J].系统工程理论与实践,2004,24(1): 57-62. TIAN Jun, ZHANG Peng-zhu, WANG Kan-liang, et al. The integrating model of expert’s opinion based on Delphi method [J]. System Engineering Theory and Practice, 2004, 24(1): 57-62. [9] 常建娥,蒋太立.层次分析法确定权重的研究[J].武汉理工大学学报:信息与管理工程版,2007,29(1): 153-156. CHANG Jian-e, JIANG Tai-li. Research on the weight of coefficient through analytic hierarchy process [J]. Journal of Wuhan University of Technology: Information and Management Engineering, 2007, 29(1): 153-156. [10] 万俊,邢焕革,张晓晖.基于熵理论的多属性群决策专家权重的调整算法[J].控制与决策,2010, 25(6):907-910. WAN Jun, XING Huan-ge, ZHANG Xiao-hui. Algorithm of adjusting weights of decision-makers in multi-attribute group decision-making based on entropy theory [J]. Control and Decision, 2010, 25(6): 907-910. [11] CHEN Ting-yu, LI Chia-hang. Determining objective weights with intuitionistic fuzzy entropy measures: a comparative analysis [J]. Information Sciences, 2010, 180(21): 4207-4222. [12] COOK W D, KRESS M. A multiple-criteria composite index model for quantitative and qualitative data [J]. European Journal of Operational Research, 1994, 78(94): 367-379. [13] 周荣喜,范福云,何大义,等.多属性群决策中基于数据稳定性与主观偏好的综合熵权法[J].控制与决策,2012,27(8): 1169-1174. ZHOU Rong-xi, FAN Fu-yun, HE Da-yi, et al. Integrated entropy weight method based on data stability and subjective preference in multi-attribute group decision-making [J]. Control and Decision, 2012, 27(8): 1169-1174. [14] HERRERA F, MARTINEZ L. A 2-tuple fuzzy linguistic representation model for computing with words [J]. IEEE Transactions on Fuzzy Systems, 2001, 8(6): 746-752. [15] OPRICOVIC S. Multicriteria optimization of civil engineering systems [J]. Faculty of Civil Engineering, 1998, 2(1): 5-21. [16] OPRICOVIC S, TZENG G H. Multicriteria planning of post-earthquake sustainable reconstruction [J]. Computer Aided Civil and Infrastructure Engineering, 2002, 17(3): 211-220. [17] SANAYEI A, MOUSAVI S F, YAZDANKHAH A. Group decision making process for supplier selection with VIKOR under fuzzy environment [J]. Expert Systems with Applications, 2010, 37(1): 24-30. [18] SALEHI K. A hybrid fuzzy MCDM approach for project selection problem [J]. Decision Science Letters, 2015, 4(1): 109-116. [19] 萨日娜,张树有.复杂产品设计方案联合变权群决策方法[J].浙江大学学报:工学版,2013, 04(4): 711-719. SA Ri-na, ZHANG Shu-you. Conjoint variable weight group decision method for complex product scheme design [J]. Journal of Zhejiang University: Engineering Science, 2013, 04(4): 711-719. [20] 王强英.三角直觉模糊多属性群决策方法及其在供应商选择中的应用[D].南昌:江西财经大学,2014. WANG Qiang-ying. Triangular intuitionistic fuzzy multiple attribute group decision making method and its application in supplier selection [D]. Nanchang: Jiangxi University of Finance and Economics, 2014. [21] OPRICOVIC S, TZENG G H. Compromise solution by MCDM methods: a comparative analysis of VIKOR and TOPSIS [J]. European Journal of Operational Research, 2004, 156(2): 445-455. [22] RAO R V, PATEL B K, PARNICHKUN M. Industrial robot selection using a novel decision making method considering objective and subjective preferences. rob auton syst [J]. Robotics and Autonomous Systems, 2011,59(6): 367-375. [23] 张丽霞,侍克斌.施工网络进度计划的多目标优化[J].系统工程理论与实践,2003,23(1): 56-61. ZHANG Li-xia, SHI Ke-bin. Construction network’s optimization under multi-goal conditions [J]. System Engineering Theory and Practice, 2003, 23(1): 56-61. Selection of construction project schedule alternatives based on improved VIKOR method WANG Ren-chao, DENG Jian, CAO Ting-ting (StateKeyLaboratoryofHydraulicEngineeringSimulationandSafety,TianjinUniversity,Tianjin300072,China) A method based on improved VIKOR was proposed in order to solve the decision makers’ preference on evaluation criteria. The method used language variables to qualitatively evaluate various criteria and used the two-tuple linguistic to aggregate experts’ evaluation on criteria. Decision makers’ subjective preference and criteria objective weight were considered to make the criteria’s weight more reasonable. Because the decision maker wants a solution that is the closest to the ideal, the alternatives are evaluated according to all established criteria. The VIKOR method was used to solve the network schedule optimization plans decision making problem, through measuring the distance between the alternatives and the best values to get the compromised result. An example analysis was given to illustrate the effectiveness and practicability of the proposed method. network schedule optimization; multi-criteria group decision making; subjective preference; two-tuple linguistic; VIKOR method 2015-09-08. 王仁超(1963—),男,教授,从事大型工程系统分析、项目管理及计算机仿真研究.ORCID: 0000-0003-4331-9620. E-mail:renchao1881@vip.sina.com 10.3785/j.issn.1008-973X.2016.10.025 TU 722 A 1008-973X(2016)10-2025-06 浙江大学学报(工学版)网址: www.zjujournals.com/eng

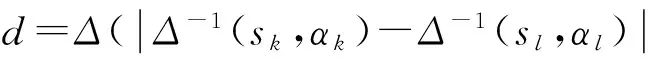




2 网络进度计划优化决策方法


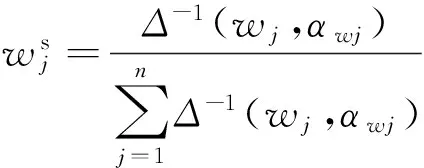
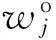

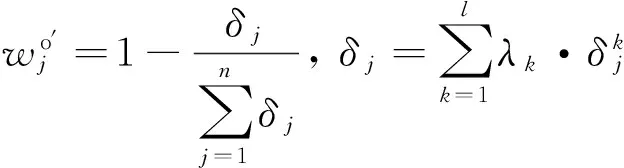
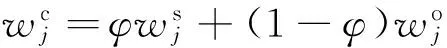
3 算例分析






4 结 语
