大波段Z形镍钛自膨胀支架的植入压缩和脉动服役行为的有限元分析*

王伟强，张会娟，齐 民

(大连理工大学 材料科学与工程学院，辽宁 大连 116024)



大波段Z形镍钛自膨胀支架的植入压缩和脉动服役行为的有限元分析*

王伟强，张会娟，齐 民

(大连理工大学 材料科学与工程学院，辽宁 大连 116024)

超弹性镍钛合金支架在植入前的大幅度压缩和脉动受载过程对支架的安全性有重要影响。大幅度压缩会使支架局部产生较大的应变，当此应变超出了材料的应变极限时会使材料发生永久性变形。支架植入体内后，血管的脉动会使支架受到周期的压缩载荷，并形成疲劳循环。针对大波段Z形支架，运用有限元法分析了支架V形连接弧半径和支撑筋长度对支架压缩过程和脉动循环过程受力的影响。结果表明，支架在植入压缩和脉动服役时，V形连接弧内侧受压缩，外侧受拉伸；增加支架支撑体长度和连接弧半径均使支架的压缩应变减小并使其耐疲劳性增加。另外在评价支架安全性时，不仅要分析支架的长期耐疲劳性，也要考虑其在植入前大幅度压缩时的受力情况。

镍钛合金；自膨胀支架；压缩；疲劳；有限元分析

0 引 言

血管支架根据其服役机制可以分为两大类，球囊膨胀式和自膨胀式支架。自膨胀式支架最大的优势在于可以对血管形成持续的低的外推力，可在支撑血管的同时，降低对血管的损伤。自膨胀支架服役主要运用的是材料的超弹性效应，支架在发生大的变形之后可以弹性恢复，特别适用于服役时出现大变形的部位，如膝盖、颈动脉、浅表动脉等外周血管部位。

自膨胀式支架植入是通过将大直径支架大幅度压缩进入小的输送导管，之后从输送器中释放支撑血管。支架在体内的作用主要是支撑血管形成新的血流通道。对于血管瘤的治疗，运用覆膜支架还可以对血管瘤形成密封的腔，阻止血流进入瘤腔造成进一步的膨胀弱化。因此支架的受力主要包括装入输送器时的大幅度压缩以及植入之后压缩状态下的脉动受载。但研究表明，大幅度压缩[1]以及循环受载[2]都对支架有很重要的影响。对于镍钛合金自膨胀式支架，这些研究部分侧重于实验测试[1,3]，部分侧重于有限元法，或是将实验测试与有限元分析结合起来进行探究[2,4]。但是，对应的结构多数基于激光切割成型支架，对大血管金属丝热处理定型支架的分析还很少。本文主要是通过有限元法，对大血管金属丝Z形支架的压缩和疲劳行为进行分析探讨，为以后支架的选择和设计提供借鉴。

1 材料和方法

1.1 材料属性和单元

超弹性镍钛合金最显著的特点就是其拉伸或压缩时应力-应变行为存在刚度的“偏置”，加载和卸载时材料响应不同。此刚度的变化是由材料应力诱发马氏体相变引起的。在一定受力条件下，材料通过相变缓解大变形时的应力集中，在应力-应变曲线上出现对应正相变(A到M)的加载应力平台，而卸载时出现对应的逆相变(M到A)应力平台。

本模拟基于ABAQUS 6.12软件，表1为模拟中镍钛合金支架的材料参数[5]。

在软件实现上，主要运用ABAQUS内置的镍钛合金超弹性本构模型(C3D8R)。对于压缩支架的工具，模型采用surface单元中SFM3D4R。支架体内膨胀时与其接触的血管材料的参数见表2[6]。

表2 血管材料参数[6]

1.2 模拟方法

1.2.1 支架几何

模拟的支架结构是基于金属丝热处理定型的Z形大波段支架。支架3D模型通过Pro/Engineer Wildfire 5.0作图。初始几何参数如下：金属丝绕制时的V形弯曲半径或连接弧半径R=0.9 mm，支架支撑体长度L=12 mm，支架环向V形数n=6，支架直径dstent=27.38 mm，镍钛金属丝直径dwire=0.44 mm(见图1(a))。在实际使用中，完整的支架结构是由金属环的排列组合构造而成。其中的直线型支架一般如图1(b)所示。临床使用中支架还包括固定装置，如倒钩、端部的喇叭口状结构等。

图1 支架的支撑单元与支架环、支架环的排列组合

Fig 1 Stent supporting unit and the stent ring, alignment of stent rings

1.2.2 模拟控制过程

支架的设计直径一般大于血管直径，在支撑血管的同时起到固定支架的作用，因此支架在体内相对于原始成型态一直处于压缩状态。模拟主要通过两个步骤进行过程控制。

第一步，支架压缩进入输送器过程。模拟通过压缩鞘的位移边界进行控制，将支架从原始直径压缩到输送器尺寸(22Fr)。随后支架释放，在内部储存的弹性变形能的驱动下自发膨胀，与血管接触。

第二步，支架在体内脉动受载过程。支架的脉动受载是和血管顺应性相关的一个过程。血管顺应性是指在压力作用下血管容积增大而不破裂的一种特性,是衡量血管腔可扩张度的重要指标。血管的顺应性是由病人的年龄和血管疾病类型等因素决定的。对年轻健康血管，最差估计是在13.3 kPa压力下血管直径有5%的变化[7]。模拟中通过位移控制，在柱坐标系下，控制压缩鞘的径向位移，使支架的脉动幅值为血管直径变化的±2.5%。

模拟中，设置支架的长轴方向为柱坐标的Z方向。为避免支架在Z方向产生大的刚性位移致使计算不收敛，设置支架的端部节点Z方向位移为0。另外由于支架、血管和鞘均是周向对称的，为节省计算资源，均选取部分建模，在截取截面上设置周向对称边界条件。支架和鞘以及支架和血管的接触均运用主从接触面算法，设置接触面的摩擦系数分别为0和0.2[5]。

1.2.3 有限元参数化设计

模拟运用控制变量法探究了两个参数变化(连接弧半径R和支撑体长度L)对支架受载的影响，具体的参数化设置如表3所示。

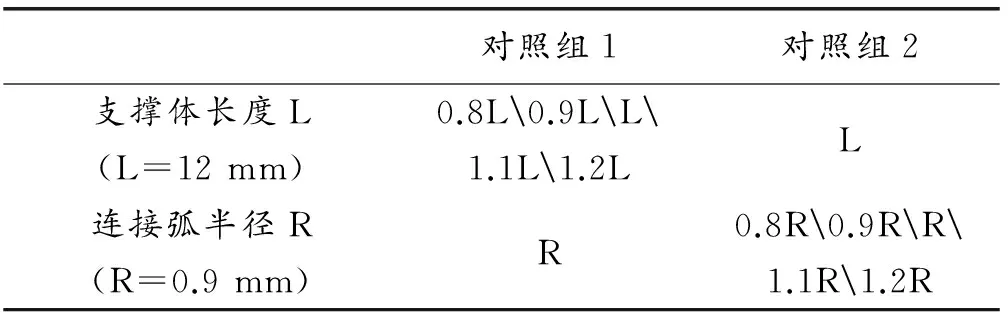
表3 参数化设计

1.2.4 分析方法与数据表征

支架压入输送器，支撑体发生大幅度的弯曲，产生大的拉伸或压缩应变，并在压缩到最小直径时应变达到最值。若该值接近材料的应变极限，在支架装入输送器之后的保存、运输过程中就容易发生蠕变，产生不可恢复变形的可能，并在释放之后超弹性有所丧失。因此本文对支架压缩过程的分析主要是基于支架在压缩到最小尺寸时的压缩应变。

植入体内后，支架的平均应变是支架和血管相互作用，受到血管压缩引起的[8]。因此，平均应变受支架植入后受压程度的影响。支架直径超出血管直径的程度不同，支架的平均受压程度也不同，对应产生的平均应变不同。而交变应变是由支架随血管脉动受力引起的，是评价支架疲劳的主要参数[9]。美国食品药物管理局(FDA)在2005年对血管内支架的指导文件中指出，对支架材料疲劳的进一步分析要能得出相应的参数，比如，疲劳极限和疲劳-寿命图。这些指导文件为支架的疲劳分析指明了方向。本文对支架疲劳的分析也是基于支架脉动受力时的交变应变值。

2 结果与讨论

2.1 支架大幅度压缩过程

由于所有对比组支架的应力-应变云图相似，模拟提取了R=0.9 mm，L=12 mm支架在压缩到目标尺寸时的应力-应变云图，如图2，3所示。由应力-应变云图分布可看出，支架在压缩到小直径过程中，支架受力主要集中于合金丝弯曲圆弧内外侧。并且通过提取的应力-应变云图可知，最大拉伸主应力-应变的节点位于支架外侧，最大压缩主应力-应变的节点位于弯曲圆弧内侧。James等研究指出[1]，金属丝支架的V形结构在大幅度压缩时会在弯曲金属丝内侧形成微裂纹导致压缩损伤，并会对支架后期的受力产生影响。因此模拟提取了不同设计参数的支架在压缩到最小尺寸时的压缩应变值，见表4。

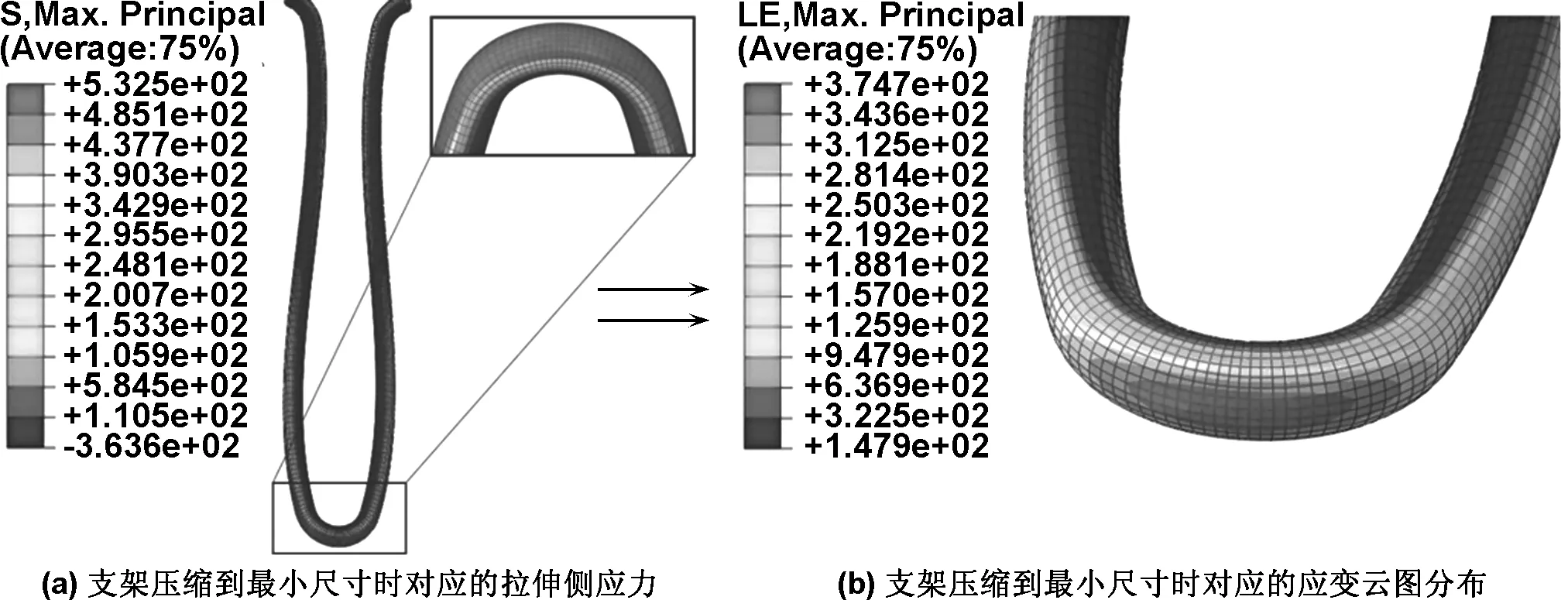
图2 支架压缩到最小尺寸时对应拉伸侧应力和应变云图分布

Fig 2 The cloud distribution of stress and strain in tensile side of stent strut when compressed to minimum size

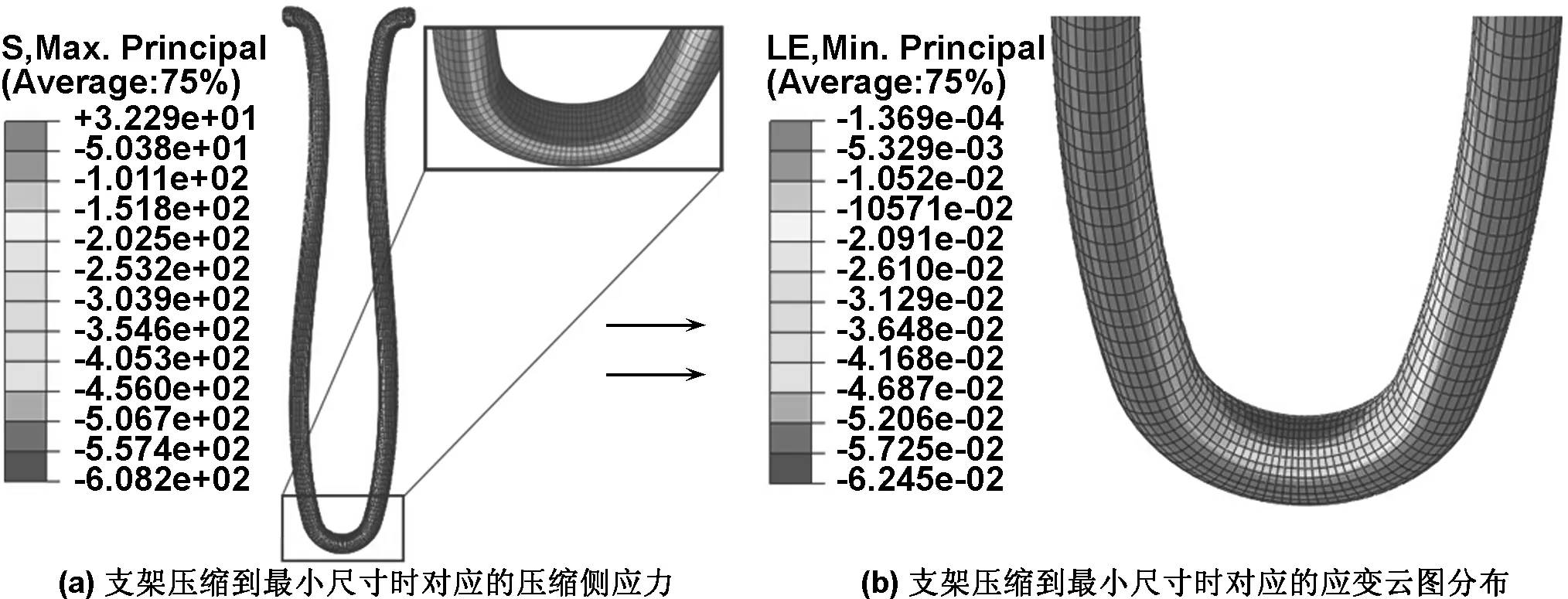
图3 支架压缩到最小尺寸时对应压缩侧应力和应变云图分布

Fig 3 The cloud distribution of stress and strain in compression side of stent strut when compressed to minimum size

表4 支架几何参数对压缩主应变的影响

Table 4 The influence of stent geometry on compression principal strain

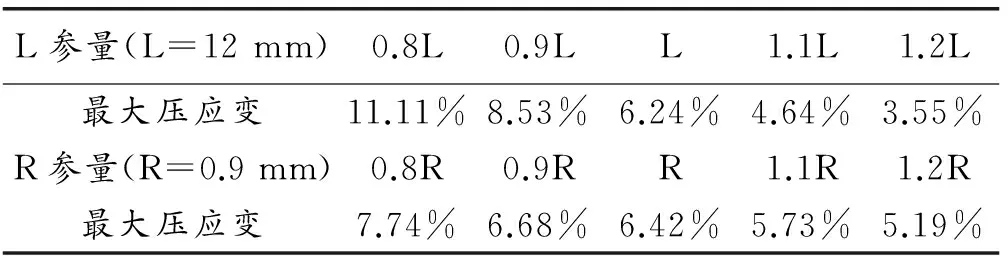
L参量(L=12mm)0.8L0.9LL1.1L1.2L最大压应变11.11%8.53%6.24%4.64%3.55%R参量(R=0.9mm)0.8R0.9RR1.1R1.2R最大压应变7.74%6.68%6.42%5.73%5.19%

从表4数据可知，支架的支撑体长度和连接弧半径对其压缩力学响应的影响很大。控制支架的V形连接弧半径，支架支撑体长度从9.6 mm增加到14.4 mm时，支架的最大压缩应变值从11.11%减小到3.55%。有文献指出[10]，单晶超弹性镍钛合金最大可恢复应变可达到10.7%，多晶时可达8%。对于0.8L、0.9L支架，最大压缩应变为11.11%和8.53%，已经超出了材料的弹性恢复应变范围，即支撑体长度为9.6和10.8 mm的支架超弹性功能不能保证，在压缩进入输送器的过程中很可能出现不可逆变形。同时需要注意的是，在镍钛合金的单向拉伸与压缩曲线中，其拉伸和压缩时的力学响应是不对称的，材料在压缩时加载平台所需的应力更高，同时压缩加载时转变应变变小(平台变短)[11]。这意味着，材料在压缩状态下的可恢复应变小于拉伸态。

对于支架连接弧半径对压缩响应的影响，从表4可看出，控制支架的支撑体长度，当连接弧半径从0.72 mm变化到1.08 mm时，支架压缩最大应变值从7.74%减小到5.19%。即V形连接弧半径的增加可以使支架的大幅度压缩更安全。但连接圆弧半径并不是越大越好。圆弧半径太大，会导致支架压缩进入输送器的过程中相邻支撑体之间自接触的提前发生，对支架、输送器以及血管的尺寸配合产生很大的影响。

2.2 支架脉动受载过程

鉴于所有对照组支架的应力-应变分布结果相似，模拟提取了R=0.9 mm，L=12 mm支架在血管收缩压和舒张压两个状态结束时支架上所有节点的应变值。然后通过ABAQUS中python脚本后处理，计算出所有节点在两状态结束时的平均应变(图4)和交变应变(图5)。

从图4中可以看出，脉动受载时，平均应变云图中，拉伸应变集中区域位于支架弯曲圆弧外侧，压缩应变集中区域位于圆弧内侧。同时在交变应变云图(图5)中，较大值区域位于支架V形连接弧的内侧。前人研究指出[9]，交变应变对支架的疲劳有着更直接的关系。依据FDA文件指示，血管支架的疲劳可以用疲劳寿命图表示，提取脉动时支架上每个节点的平均应变和交变应变，将节点平均应变和交变应变值表示在疲劳寿命图中，位于疲劳极限值以下的结果对应节点是安全的。

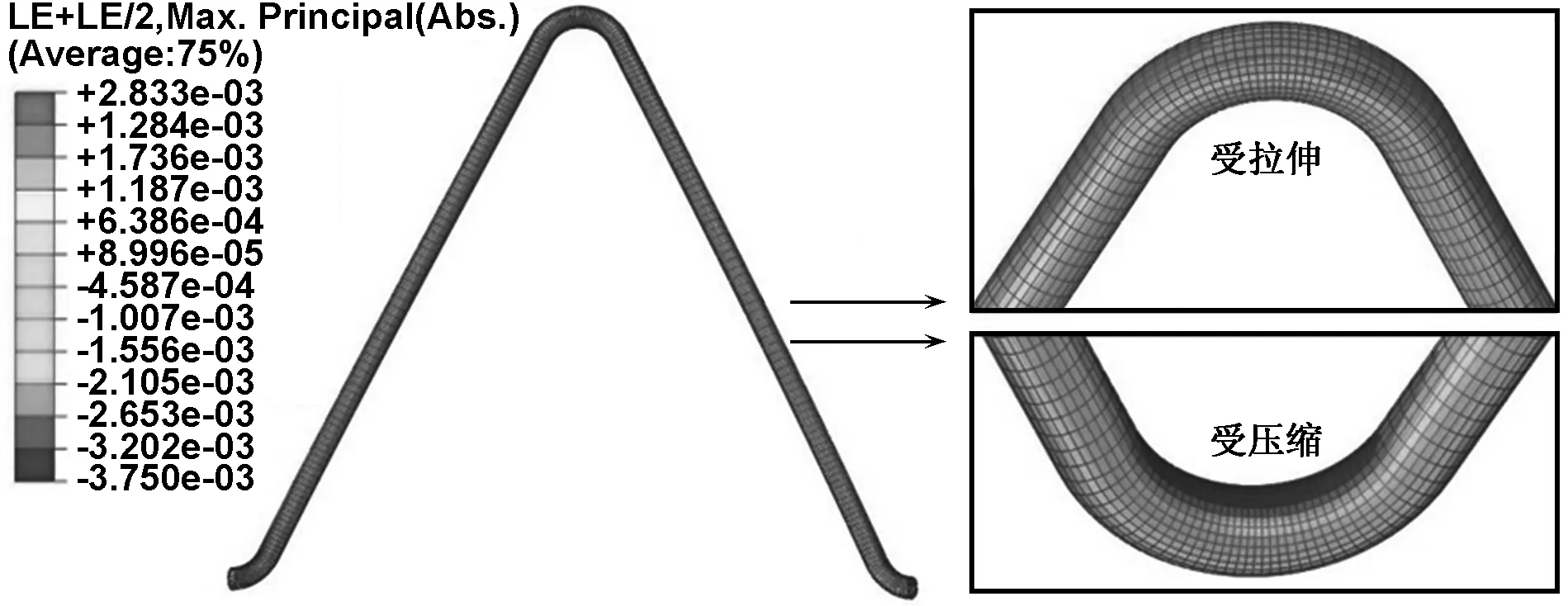
图4 支架在血管扩张压和收缩压下的平均应变

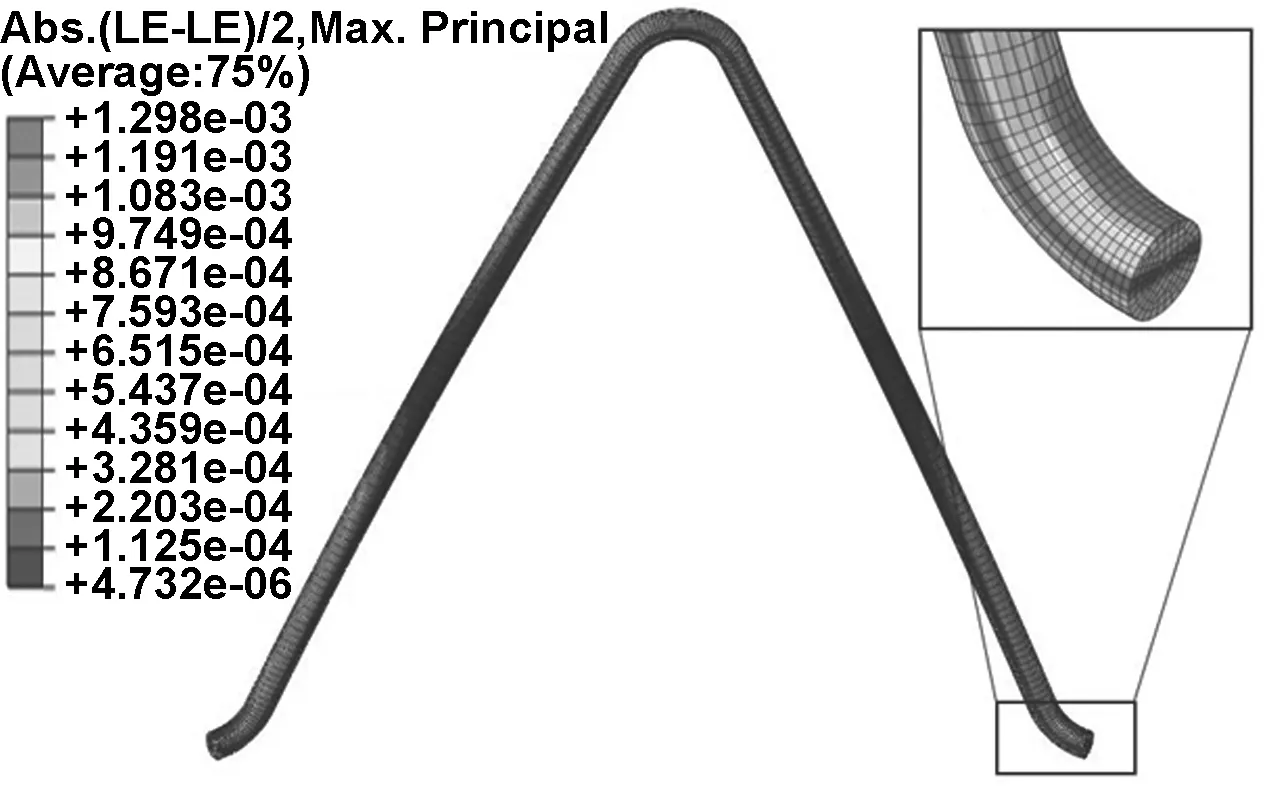
图5 支架在血管扩张压和收缩压下的交变应变

Fig 5 The alternating strain of stent on diastole and systole

另外一种表示支架疲劳的方法是疲劳安全系数[11]，其计算公式如下

Fatigue Safety Factor(FSF)=εallow/εalt

(1)

其中，εallow表示支架的疲劳极限，即支架发生疲劳失效的临界交变应变，εalt表示支架节点脉动时的交变应变，当FSF值大于1时表明支架安全。Pelton等通过实验的方法得出，支架的疲劳极限一般在0.4%[12]。但作者还指出，支架在平均应变大于1.5%或是2%时疲劳极限增加，原因主要是与材料的应力诱发马氏体相变有关。

对于本次模拟，从交变应变云图(图5)可以看出，支架在脉动时，交变应变的最大值是0.13%，提取支架节点平均应变最大为0.28%，小于1.5%，通过公式(1)计算得出，支架最小疲劳安全系数为3.08，说明支架是安全的。同时也提取并计算了不同参数设计支架的结果，见表5。从表5结果看出，支架支撑体长度和支架的连接圆弧半径对其疲劳安全的影响很大。支架支撑体长度从9.6 mm增加到14.4 mm支架的疲劳安全系数对应地从1.47变化到4.32。当连接弧半径从0.72 mm变化到1.08 mm时，支架疲劳安全系数对应地从2.62变化到3.45。由此可知，Z形支架的疲劳安全性可以通过调整连接弧半径和支撑筋长度来改变，增加V形连接弧半径和支撑筋的长度均可以增加支架的耐疲劳性。

表5 支架关键几何参数对疲劳安全系数的影响

Table 5 The influence of key geometric parameters of stent on its fatigue safety factor

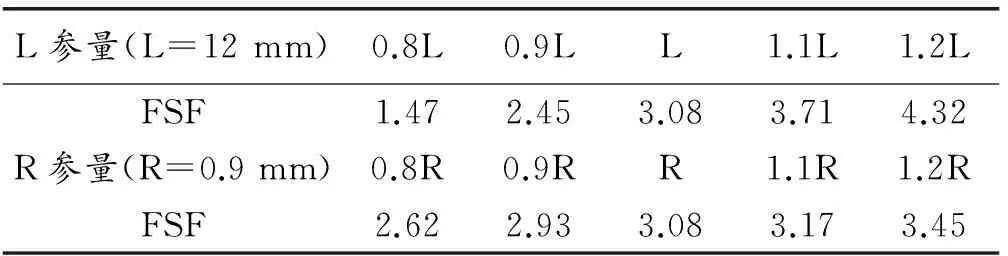
L参量(L=12mm)0.8L0.9LL1.1L1.2LFSF1.472.453.083.714.32R参量(R=0.9mm)0.8R0.9RR1.1R1.2RFSF2.622.933.083.173.45

综合对比支架大幅度压缩过程和支架的脉动受载过程可知，对于0.8和0.9L的支架来说，在脉动受力中的疲劳安全系数均是大于1的，亦即都是符合支架设计要求的。但是在大幅度压缩时上述两设计参数支架又是不安全的。因此支架的安全性分析不仅要考虑支架脉动时的疲劳安全性，还要考虑大幅度压缩对支架后期超弹性功能实现的影响。

3 结 论

运用参数化的方法分析了大波段Z形镍钛自膨胀支架在植入压缩过程和体内脉动过程的受力，通过分析可以得出以下结论：

(1) 支架植入体内整个过程，受力集中部位是在支架丝弯曲的部位，且弯曲圆弧内侧受压，外侧受拉。

(2) 支架的支撑体长度和连接圆弧半径对支架压缩力学响应影响很大。减小支撑体长度、减小连接圆弧半径会使圆弧内侧压缩应变大大增加，提高支架服役失效的风险。

(3) 支架支撑体长度和连接圆弧半径对支架脉动服役影响也很大。增加支撑体长度、增加连接圆弧半径会使支架安全系数增加。

(4) 单纯地分析支架在脉动过程中的耐疲劳性是不够的，还需要结合支架在大幅度压缩时的受力分析。若支架的应变大于材料的可恢复应变极限，会对支架的超弹性性能造成不良影响。

[1] James B, Murray S, Saint S. Fracture characterization innitinol[A]. SMST-2003 Proceedings of the International Conference on Shape Memory and Superelastic Technologies[C]//USA: SMST Society Inc, 2004. 9: 321-329.

[2] Rebelo N, Gong X Y, Hall A, et al. Finite element analysis on the cyclic properties of superelastic nitinol[A]. Proceedings of the International Conference on Shape Memory and Superelastic Technologies[C]//USA: SMST Society Inc, 2006.157-163.

[3] Dyet J F, Watts W G, Ettles D F, et al. Mechanical properties of metallic stents: how do these properties influence the choice of stent for specific lesions[J]. Cardiovascular and Interventional Radiology, 2000, 23(1): 47-54.

[4] Rebelo N, Gong X Y, Hall A, et al. Finite element analysis on the cyclic properties of superelastic nitinol[A]. Proceedings of the International Conference on Shape Memory and Superelastic Technologies[C]//USA: SMST Society Inc, 2006.157-163.

[5] De Bock S, Iannaccone F, De Santis G, et al. Virtual evaluation of stent graft deployment: a validated modeling and simulation study[J]. Journal of the Mechanical Behavior of Biomedical Materials, 2012, 13: 129-139.

[6] Kleinstreuer C, Li Z, Basciano C A, et al. Computational mechanics of nitinol stent grafts[J]. Journal of Biomechanics, 2008,41(11): 2370-2378.

[7] Duerig T, Pelton A, Stockel D. An overview of nitinol medical applications[J]. Materials Science and Engineering: A, 1999, 273: 149-160.

[8] Zheng Y F, Zhao L C. Biomedical nitinol[M]. Beijing: Science Press, 2004:195.

郑玉峰, 赵连成. 生物医用镍钛合金[M]. 北京: 科学出版社, 2004:195.

[9] Pelton A R, Schroeder V, Mitchell M R, et al. Fatigue and durability of Nitinol stents[J]. Journal of the Mechanical Behavior of Biomedical Materials, 2008, 1(2):153-164.

[10] Yang D Z, Wu M X. Biomedical applications of Ni-Ti shape memory alloy[M]. Beijing: Metallurgical Industry Press,2003:64.

杨大智, 吴明雄. Ni-Ti形状记忆合金在生物医学领域的应用[M]. 北京: 冶金工业出版社, 2003:64.

[11] Azaouzi M, Makradi A, Belouettar S. Deployment of a self-expanding stent inside an artery: a finite element analysis[J]. Materials and Design, 2012, 41: 410-420.

[12] Pelton A R, Gong X Y, Duerig T. Fatigue testing of diamond-shaped specimens[A]. Proceedings of the International Conference on Shape Memory and Superelastic Technologies[C]//USA: SMST Society Inc, 2004.293-302.

Finite analysis of the compression in deployment and pulsating service behavior of the big band and Z-shaped self-expanding stent

WANG Weiqiang，ZHANG Huijuan， QI Min

(School of Materials Science and Engineering, Dalian University of Technology, Dalian 116024, China)

The significant compression before implantation and pulsating load process of the super-elastic nitinol stent have important impacts on its security application. Significant compression can result in substantial strain in local area of the stent, and when the strain exceeds the strain limit of the material, the permanent deformation will occur. While in service, the stent will receive a periodic pulsating compressive load, and undergo fatigue cycles. Regarding the big band Z-stent, in this paper, we make use of the finite element method to analyze the influence of V-type connector radius and the length of the support strut of stent on its compression and pulsation cycle. The results showed that during the implantation and pulsating process, V-type connector is compressed inside and stretched outside; increasing the length of the support strut and the arc radius will reduce the compressive strain and increase fatigue resistance. Moreover, to evaluate the safety of the stent, it needs to analyze not only the long-term fatigue resistance, but also the significant compression deformation before implantation.

nitinol; self-expanding stent; compression; fatigue; finite element analysis

1001-9731(2016)04-04023-05

国家自然科学基金资助项目(51371042)；中央高校基本科研业务费专项资金资助项目(DUT13JB06)；高等学校博士学科点专项科研基金资助项目(20130041110005)

2015-05-19

2015-10-26 通讯作者：王伟强，E-mail: wangwq@dlut.edu.cn, 齐 民

王伟强 (1974-)，男，辽宁大连人，副教授，博士，从事生物医用材料研究。

TB381

A

10.3969/j.issn.1001-9731.2016.04.005