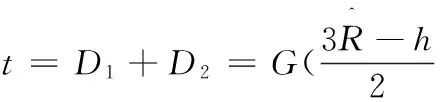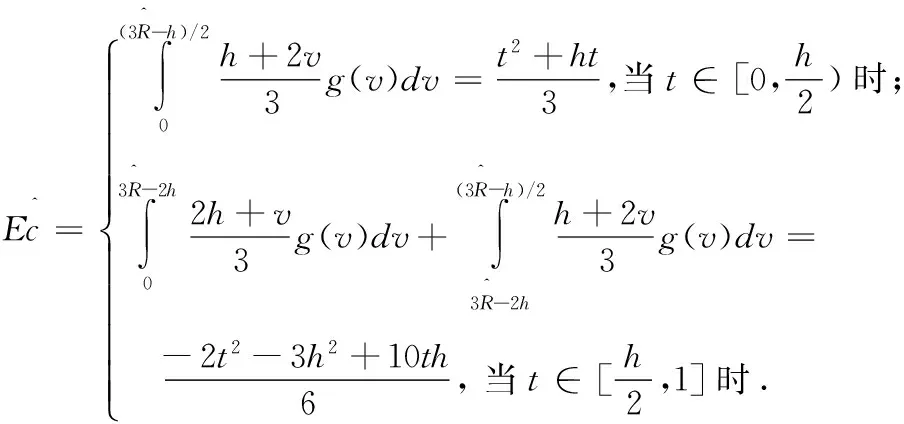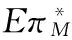基于在线报价与固定价格的闭环供应链最优决策研究
2016-12-03李建斌朱梦萍
李建斌,朱梦萍,戴 宾
(1.华中科技大学管理学院,湖北 武汉 430074; 2.武汉大学经济与管理学院,湖北 武汉 430072)
基于在线报价与固定价格的闭环供应链最优决策研究
李建斌1,朱梦萍1,戴 宾2
(1.华中科技大学管理学院,湖北 武汉 430074; 2.武汉大学经济与管理学院,湖北 武汉 430072)
本文研究闭环供应链中制造商在逆向渠道采用单一在线报价,两次在线报价和固定价格模式来回收折旧品的最优决策问题。研究表明,虽然两次报价比单一报价给消费者带来更高的期望效用,然而从制造商的利润来看,两次报价是较劣的策略。制造商选择单一报价和固定价格的回收模式,主要取决于再制造节约成本和预设价格的上限。如果预设价格的上限低于某临界值,随着节约成本增加,制造商的最优策略从固定价格转变为单一报价;如果预设价格的上限超过该临界值,制造商的最优策略一直是固定价格模式。最后,通过算例分析进一步探讨了重要参数对制造商利润的影响,揭示了制造商可以向消费者传递更低的预设价格上限来获利的管理意义。
闭环供应链;再制造;在线报价;固定价格
1 引言
随着社会的发展,资源危机和环境问题日益严重,可持续发展受到广泛的关注,越来越多的企业开始采用折旧品的回收再制造策略,如戴尔、IBM等,因为这不仅节约了生产成本,同时也能塑造良好的企业形象,因此,闭环供应链的研究得到了国内外学者的广泛关注。Savaskan等[1]分别探讨了制造商、零售商和第三方负责回收时供应链成员的最优决策,发现零售商负责回收的渠道结构最优;之后,其又进一步研究了多个零售商竞争环境下的回收渠道设计问题[2]。Majumder等[3]通过建立两阶段的博弈模型研究了制造商和再制造商的回收竞争问题。Kaya[4]考虑了基于制造商激励的回收数量情形下制造商的最优生产决策问题。De Giovanni等[5]指出再制造具有降低生产成本(运作层面)和提高需求(市场层面)的双重作用。公彦德等[6]基于单一制造商和同时存在销售、回收竞争的两个销售商组成的闭环供应链系统,对比了制造商回收和销售商回收两种回收模式下闭环供应链的最优策略和系统效益。林杰等[7]以双销售渠道和双回收渠道并存的闭环供应链为背景,研究和对比了不同市场力量结构对供应链各节点企业最优策略的影响。黄祖庆等[8]研究了销售商负责回收的直线型闭环供应链中回收行为的驱动因素以及不同决策结构对供应链效率的影响。丁斌和马海庆[9]研究了供应商是否选择参与零部件回收再制造的两种闭环供应链结构,发现再制造战略对批发价决策的影响与产品的市场需求状况有关,对零售价决策的影响与回收风险状况有关。聂佳佳[10]分别研究了再制造商垄断和存在竞争对手的情形下,再制造商需求信息预测对回收再制造的影响,发现垄断的再制造商进行需求信息预测总是有利可图的。王文宾和邓雯雯[11]研究了无政府介入、奖惩机制下以及税收-补贴机制下逆向供应链的决策,发现奖惩机制比税收-补贴机制更有效。以上文献均假设再造品与新产品完全相同,而王文宾等[12]将再造品与新产品加以区分,对比研究了零售商回收和第三方回收情形下的回收努力程度和产品定价。类似地,马卫民和赵璋[13]分析研究了以旧换新补贴对具有不同等级产品闭环供应链的影响,发现以旧换新补贴使以旧换新消费者受益的同时,损害了初始消费者的利益。曹晓刚等[14]假设消费者对传统零售渠道和网络直销渠道需求偏好的不一致,研究了双渠道闭环供应链的定价及协调决策。Xiong Yu等[15]建立了制造商和零售商回收零部件的模型,并从不同角度比较了两种模型的绩效。陈章跃[16]等考虑了面对策略型顾客时,再制造品的质量水平对闭环供应链的产品价格、利润、消费者剩余的影响。
现有关于闭环供应链的研究大多集中在定价、渠道竞争以及回收渠道结构的选择(制造商回收,零售商回收和第三方回收),较少有人研究回收环节的定价模式。随着Internet的出现以及它在电子商务中的广泛应用,一些企业开始尝试创新性的定价模式,如1998年Priceline创建了在线报价(Name-your-own-price,NYOP)模式来销售机票、酒店客房等。消费者在网上对需要的商品进行报价,该报价只要高于公司内部制定的预设价格即可交易成功,反之,消费者不能购买到商品。该模式使得Priceline在激烈的美国市场竞争中脱颖而出,同时,该公司也曾经做过一些改变,允许消费者对同一件商品重复报价。这一交易模式的出现激发了许多学者的研究兴趣。Hann等[17]研究了NYOP模式下消费者的行为,表明重复报价会产生大量的摩擦成本。Fay[18]发现在某些条件下,从销售商的利润来看,两次报价优于单一报价,且固定价格优于在线报价。Terwiesch等[19]运用动态规划模型得出了消费者的最优报价次数和报价值以及最优预设价格。Cai等[20]探讨了多渠道、多种报价选择、库存有限、库存充足等多种情形下NYOP销售商的最优预设价格。Shapiro[21]假设消费者是风险规避的,发现对于垄断销售商而言,在线报价优于固定价格,并进一步探讨了存在替代销售商时NYOP的绩效。Chen等[22]考虑两个竞争的服务供应商通过一个不透明的零售商销售自己的产品,对比研究了零售商采用固定价格和在线报价两种不同销售机制对供应商的影响,发现供应商更偏好固定价格模式。周振红等[23]假定每位消费者对待购商品都有一个估价,考虑同时存在在线报价销售商和固定价格销售商,研究了报价次数对在线报价销售商预设价格的影响。
综上所述,在线报价的定价模式已被广泛研究,然而该模式仅被运用于正向供应链中。随着回收再制造活动的兴起,一些回收活动也可在网上进行,例如,中国资源再生交易网是一个专门为折旧品回收搭造的网上交易平台,包含供应和求购信息。鉴于此,本文的研究目的是将在线报价模式运用到闭环供应链的回收渠道中,对比研究回收渠道采用在线报价和固定价格两种不同模式下供应链成员的最优决策。
2 模型描述与基本假设
本文考虑某垄断制造商同时生产单一品牌的新产品和通过回收上阶段出售的旧产品进行再制造,然后将新产品和再造品以相同价格销售给消费者,消费者对两种产品的接受程度相同。制造商直接销售和直接回收。由于现实中折旧品的回收数量往往小于上期的市场需求量,因此,再造品数量不能满足市场需求,制造商必须生产一定数量的新产品。回收渠道中,制造商有两种定价模式:在线报价与固定价格(Posted price, PP),且在线报价中又进一步探讨了单一报价(Single-bid)和两次报价(Double-bid)。本文通过对比研究三种报价模式下制造商的最优决策,进而得到制造商最佳的回收定价模式。本文研究的闭环供应链模型见图1。相关参数的符号说明如表1所示。
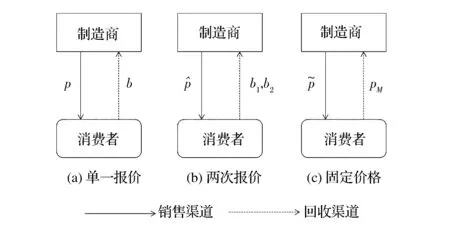
图1 不同回收定价模式下的闭环供应链模型
在正向渠道中,市场需求是价格p的线性函数,设为D=a-kp,a为市场容量,k为消费者对产品的价格敏感系数。经济学和市场营销领域相关研究支持该线性需求假设,如Vives[24]和Choi[25]。闭环供应链相关研究中,也广泛使用该假设。如Savaskan等[1-2],Bulmus等[26][27],Wei Jie等[28]。
在逆向回收过程中,本文考虑了两类不同的消费者。第一类为环保消费者,他们更重视社会效用而非自己的效用。因此,即使制造商的回收价格为0,他们也愿意将旧产品转移给制造商。第二类为非环保消费者。此时,制造商必须支付一定的“补贴”才能回收成功。不失一般性,假设环保消费者的比例为1-λ,非环保消费者的比例为λ,其中λ是公共信息。

表1 符号及含义
对于非环保型消费者,需要对其回收动机进行分析。营销学文献使用WTP(Willingness to pay)的概念来解释消费者购买产品的动机,该理论认为购买新产品能够给消费者带来一定的效用或者价值,如Park和Maclachlan[29],Schmidt等[30]。参考该概念,消费者持有折旧产品也会给其带来价值v。因此,可以认为v表示折旧品的持有价值。不同的v代表非环保消费者的异质性。如果消费者心理上“喜新厌旧”,则v较小,如果消费者对新产品和折旧产品偏好相差不大,则v较大。从制造商的角度考虑,通过逆向渠道回收折旧产品时,较小的v意味着回收成本较低,反之,则高。为刻画非环保消费者群体的异质性,假设v服从[0,1]之间的某种分布,概率密度函数为g(·),累积分布函数为G(·)。为了便于研究,本文对做了一些简化,提出了如下合理假设:
假设1新产品和再制造品的销售价格相同。
现实中,新产品和再制造品的销售价格不尽相同,这取决于产品类型等一系列原因,这两种情形也都有
相应的研究文献。本文的研究重点是回收的定价模式,因此为了简化分析,参考Savaskan等[1-2],Bulmus等[26-27],假定新产品和再制造品的市场价格相同。
假设2再制造品的单位生产成本低于新产品的单位生产成本,该假设是回收活动的经济动机。
假设3a-kcm>0。成本价格销售存在市场需求。这是闭环供应链的常见假设,如Savaskan等[1-2]。
3 在线报价模式
3.1 单一报价的情形
环保消费者只关注社会效益,他愿意无偿将旧产品还给制造商,即在NYOP的定价模式下,其报价为0。对于非环保型消费者,单一报价下,消费者报价b,制造商的预设价格为R,当b≤R时交易成功,否则,交易失败。对于风险中性的消费者,目标函数为:

(1)
其中P(b≤R)表示消费者通过在线报价(NYOP)交易成功的概率。参考Cai等[20]和Shapiro[21]的研究,预期R服从均匀分布,上界为h,下界为l,则P(b≤R)=(h-b)/(h-l)。由式(1)及一阶条件得:
b*(v)=(h+v)/2
(2)
非环保消费者的报价与折旧品的持有价值有关。持有价值越大,报价越高,且报价与预设价格的上限有关而与下限无关。
非环保消费者要想交易成功,必须满足两个条件:1)从消费者的角度,参与报价能够获得更高的期望效用;2)从制造商的角度,报价不能高于制造商的预设价格,即b*(v)≤R,得到v≤2R-h。因此,交易成功的条件为v≤2R-h,此时的回收比例为:

(3)
不失一般性,本文考虑h/2≤R≤(h+1)/2的情形,此时非环保消费者的回收比例为G(2R-h),总的回收率为τ=1-λ+λG(2R-h)。
根据非环保消费者的最优报价b*(v),可计算制造商回收单位产品产生的期望成本为:
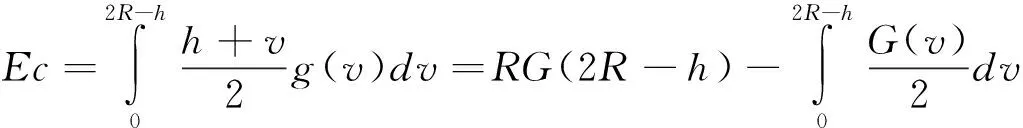
(4)
根据一阶条件,最优的价格与利润为:
(5)
(6)

1)当h/2≤Δ≤(h+1)/2时;
(7)

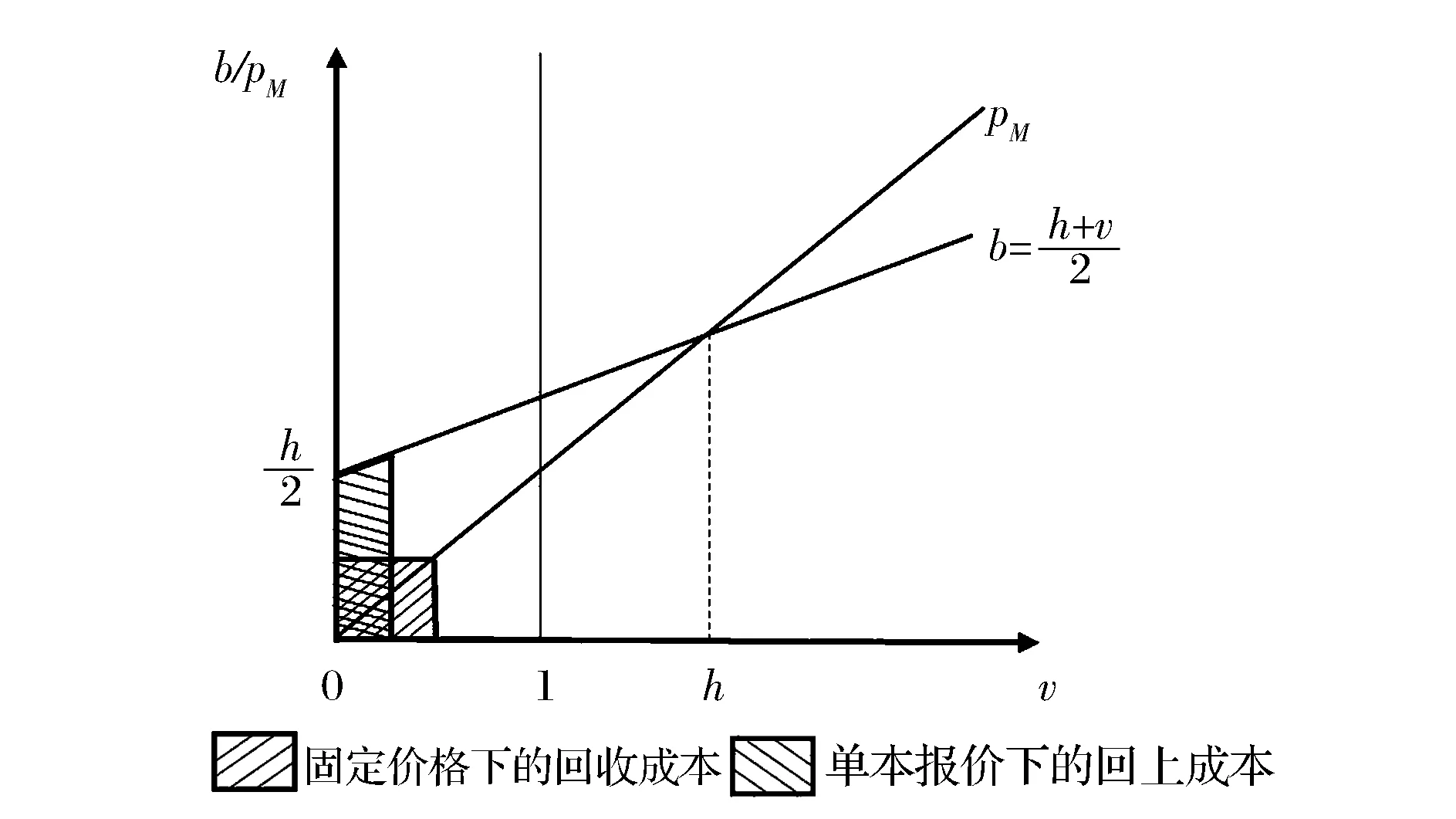
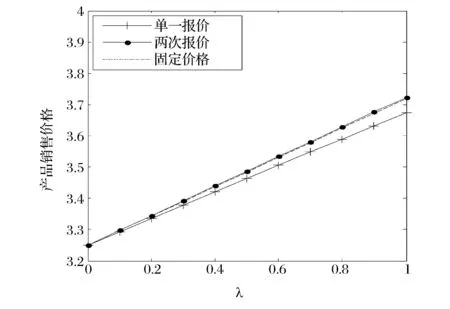
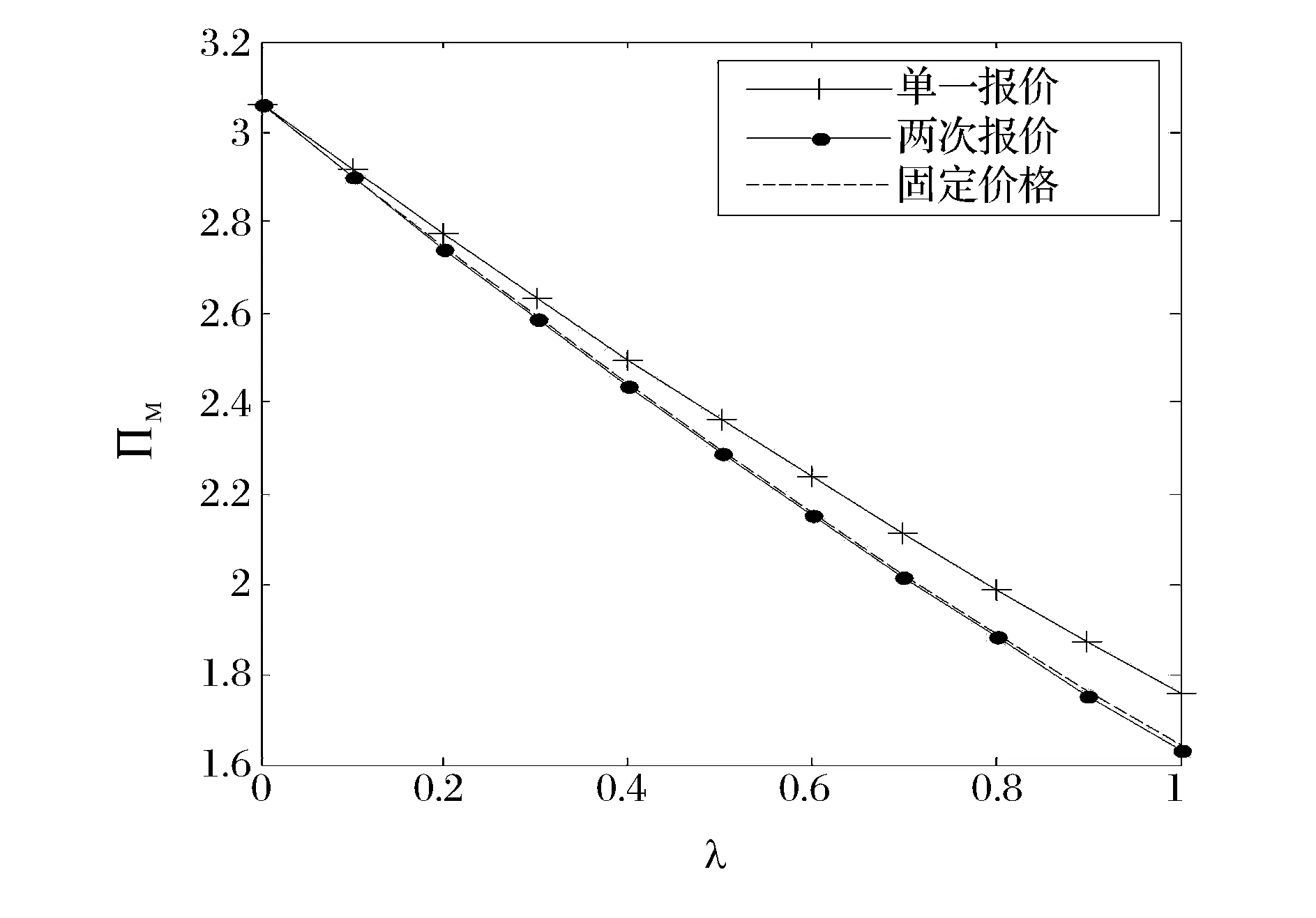
2)当Δ 3)当Δ>(h+1)/2时; (8) 命题1单一报价下,制造商的最优预设价格和最大期望利润与再制造节约成本Δ有关: (9) 由命题1可知,成本差异越大,制造商越有动机回收折旧品,因此,制定的预设价格越高。 3.2 两次报价的情形 本节分析两次报价情形下消费者的报价策略以及制造商的定价策略。环保消费者出于环保的目的,其报价为0。非环保消费者通过两次报价最大化其效用。第一次报价失败后,为了在第二次报价中成功,非环保消费者会适当地降低自己的报价。设两次报价分别为b1、b2,x为第二次报价中减少的量,两次报价中消费者的目标函数: (10) 关于两次报价模式,Cai等[20]进行了详细的分析。容易得到,式(10)关于b1、x的Hessian矩阵负定,因此,式(10)是关于b1、x的严格联合凹函数。可得到消费者的最优报价策略,如下: 命题2 两次报价下消费者的报价策略:第一次报价为b1*=(2h+v)/3,如果失败,则第二次将报价降低x*=(h-v)/3。同单一报价的报价相比,第一次报价高x*/2,而第二次报价比其低x*/2。 证明 由一阶条件可得b1*=(2h+v)/3,x*=(h-v)/3。由于b*=(h+v)/2,显然得证。 命题3 两次报价相对于单一报价而言,对非环保型消费者更有利。 (11) D2= (12) 第二次报价的回收比例为: D2= (13) (14) (15) (16) (17) (18) (19) (20) 一阶条件等价于: (21) 由于持有价值v的概率密度函数g(·)未知,二阶导无法判断正负,因此,仅能假设持有价值v的具体分布后才能求解最优预设价格。 (22) (23) (24) 最大化式(24)即等价于最大化ω(pM)=(Δ-pM)G(pM)。二阶条件为: (25) 当v服从一般分布的情况下,仅能得到单一报价下制造商的最大期望利润,见命题1。两次报价和固定价格模式下无法得出解析解,因此,进一步假设当v服从特殊的分布,如v~U(0,1),此时,单一报价的模式下制造商的最优预设价格和最大期望利润为: (26) 整合两次报价模式下的(a)、(b)两种情况,得到制造商的最优预设价格和最大期望利润为: (27) 固定价格模式下制造商的最优价格和最大期望利润为: (28) 在不同的h和Δ条件下,容易得到三种不同模式下的最优预设/回收价格,且表达式简洁,命题4容易证明。由于具体证明过程直观但繁琐,故略去。进一步观察制造商的期望利润,可以得到更重要的结论: 定理1 给定相同的回收率和销售价格,两次报价模式下,制造商需要支付的回收成本总是高于单一报价模式或者固定价格模式。从制造商的期望利润考虑,两次报价是较劣而不被选择的模式。 证明见附录。 由于单位回收成本是R或者pM的函数,实际上,R和pM决定回收率,因此单位回收成本也是回收率τ的函数。为达到相同的回收率,制造商在两次报价模式下需要支付更多的成本,因此制造商不会选择该模式。结合命题3,虽然相对于单一报价模式,消费者在两次报价模式下获得更高的期望收益,但现实中,当制造商占主导地位时,两次报价策略不会被采纳。 证明见附录。 定理2如图2所示。制造商的最优策略取决于预设价格的上限和再制造节约成本的大小。为便于理解单一报价模式和固定价格模式的区别,参考图3。对于持有价值较低的顾客,制造商通过固定价格回收成本较低,因此当制造商决定较低的回收率时,选择固定价格模式,随着回收率的提高,制造商要从那些v较大的客户手中获得折旧品,此时固定价格模式的优势减弱,更重要的是,当制造商采用固定价格模式时,为了回收更多的产品,即使对于那些v较小的客户,也同样要支付一个较高的价格,这正是固定价格回收的劣势。另一方面,制造商的回收率与再制造成本节约有关,当ΔΔ较小时,制造商缺乏回收动力,回收率低,此时制造商偏好固定价格模式;当Δ增加时,制造商希望回收更多的折旧品,此时偏好单一报价模式。 本节用算例验证上述结论的正确性,同时为了获得一些管理启示,进一步研究不同再制造节约成本和预设价格上限对制造商产品定价、回收率以及期望利润的影响。算例中的参数取值,需要满足文中的假设和条件。基于之前的分析,参数之间需要满足的条件包括max{1,3l}≤h<2,a-kcm>0等。在此基础上,将基本参数赋值为a=5,k=1,cm=3,l=0.2,λ=0.9,h和Δ的取值在不同的数值实验中变化。 图2 不同区间下制造商的最优策略 图3 单一报价和固定价格模式回收成本比较 图4 再制造节约成本对制造商销售价格的影响 由图4可知,随着Δ的增大,制造商回收的积极性增加,因此其会减小产品的销售价格来刺激市场需求,从而获得更多的回收量。图4(a)中,当h较小时,且Δ也较小时,单一报价下产品的销售价格最高;Δ较大时,固定价格下产品的销售价格最高。图4(b)中,当h较大时,单一报价下产品的销售价格始终最 高。同时,预设价格的上限h增加时,产品的销售价格在固定价格模式下不受影响,在单一报价和两次报价模式下都增加。这是由于消费者的报价和制造商的单位回收成本与h正相关,为增加边际利润,回收成本增加时,制造商会提高产品的销售价格。 制造商的期望利润与产品的销售价格有关,随着Δ的增大,销售价格减小,市场需求增加,制造商的期望利润增大。结合图4的分析,图5(a)中,当h很小时,且Δ也较小时,固定价格下产品的销售价格最低,因此期望利润最大;Δ较大时,单一报价下产品的销售价格最低,因此期望利润最大。图5(b)中,当h较大时,无论Δ为多少,固定价格下产品的销售价格始终保持最低,因此,期望利润始终最大。 进一步探究预设价格对制造商期望利润的影响,计算发现制造商的期望利润与预设价格的下限l无关,仅与上限h有关,因此探究h对三种定价模式的影响,令Δ=1.5,基本参数如上,结果如图6所示。图6验证了定理1和定理2的结论。同时发现,三种模式下,预设价格上限对制造商期望收益影响不同。制造商的利润,在固定价格模式下显然不受预设价格上限影响,在单一报价模式下随预设价格上限单调递减,两次报价模式随价格上限先降后升再降。由于两次报价模式是不被选择的模式,因此,对制造商而言,较低的预设价格上限能够带来更高的期望收益,因此,制造商的策略是向消费者传递更多关于预设价格的信息,使得消费者对预设价格有更低的期望,从而降低在NYOP模式下的报价,最终降低制造商的回收成本。 图5 再制造节约成本对制造商期望利润的影响 图6 预设价格上限对制造商期望利润的影响 图7 环保型消费者比例对产品销售价格的影响 为了进一步探究环保型消费者对闭环供应链的影响,通过改变环保型消费者的比例,分析制造商的定价和利润的变化。相关参数为a=5,k=1,cm=3,l=0.2,h=1.2,Δ=1.5,结果如图7和图8所示。 图8 环保型消费者比例对制造商利润的影响 图7和图8表明当环保型消费者比例增加时(λ减小),产品的销售价格降低,制造商的利润反而增加。主要原因是,当环保型消费者比例增加时,制造商的回收成本降低,这直接增加了其利润,同时他也有动力降低销售价格。这表明环保型消费者的存在,不仅提高了回收率(环保效益)和制造商的利润(经济效益),同时有利于消费者以更低的价格购买新产品。当所有消费者都是环保消费者时,三种模式是无差异的,而当环保型消费者比例较低时,三种模式下的决策差异明显,因此回收定价模式选择对制造商非常重要。 本文研究了垄断制造商直销和直接回收的闭环供应链中,制造商在回收渠道可以选择在线报价或固定价格两种定价模式,在线报价中允许消费者报价一次或两次,分别探讨了单一报价、两次报价和固定价格三种模式下供应链成员的最优决策,进而得出了制造商最佳的回收定价模式。研究表明,制造商回收渠道定价模式的选择与其制定的预设价格的上限以及再制造节约成本有关。同时,本文还研究了节约成本和价格上限对销售价格、回收率和制造商期望利润的影响。本文将NYOP定价机制创新性地引入到闭环供应链的背景中,得到一些新颖的结论,丰富了对闭环供应链以及NYOP定价机制的相关研究,同时对制造商合理地选择回收定价模式提供了一定的借鉴意义。 需要指出的是,当前的研究只考虑了垄断制造商直销和直接回收的简单闭环供应链模型,而现实中往往存在竞争者,如再制造商,且销售渠道和回收渠道也可以有多个。同时,本文假设消费者的持有价值服从均匀分布,现实中的分布规律还需要进一步调查研究。因此,决策者如何选择多渠道竞争环境下回收环节的定价模式,以及持有价值服从一般分布的情形可作为后续的研究问题。 附录 定理1的证明: 单一报价模式下,单位产品的期望回收成本为: (A1) 两次报价下,分为两种情况: (A2) 固定价格模式下,单位产品的期望回收成本为: (A3) (A4) 因此,此时,两次报价模式劣于固定价格模式。当回收比例较高时,即当t∈[h/2,1]时, (A5) (A6) 对于式(A5),当t与h没有约束时,最小值t2/18≥0在h=t/3时取得。当有约束时,式(A5)的最小值会更大。对于式(A6),无约束时,最小值h2/12≥0在t=h时取得。当有约束时,式(A6)的最小值会更大。因此,两次报价模式劣于固定价格模式或者单一报价模式。 定理2的证明: 证明(1)当max{1,3l}≤h<3/2时,有h/2<(h+1)/2<2; (A7) (A8) (A9) (A7) (2)当3/2≤h<2时,有h/2<(h+1)/2<2。 [1] Savaskan R C, Bhattacharya S, Van Wassenhove L N. Closed-loop supply chain models with product remanufacturing [J]. Management Science, 2004, 50(2): 239-252. [2] Savaskan R C, Van Wassenhove L N. Reverse channel design: The case of competing retailers [J]. Management Science, 2006, 52(1): 1-14. [3] Majumder P, Groenevelt H. Competition in remanufacturing [J]. Production and Operations Management, 2001, 10(2): 125-141. [4] Kaya O. Incentive and production decisions for remanufacturing operations [J]. European Journal of Operational Research, 2010, 201(2): 442-453. [5] De Giovanni P, Reddy P V, Zaccour G. Incentive strategies for an optimal recovery program in a closed-loop supply chain [J]. European Journal of Operational Research, 2016, 249(2): 605-617. [6] 公彦德, 达庆利. 销售和回收双重竞争下的闭环供应链最优决策分析 [J]. 系统科学学报, 2014, 22(2): 83-86. [7] 林杰, 曹凯. 双渠道竞争环境下的闭环供应链定价模型 [J]. 系统工程理论与实践, 2014, 34(6): 1416-1424. [8] 黄祖庆, 达庆利. 直线型再制造供应链决策结构的效率分析 [J]. 管理科学学报, 2006, 9(4): 51-57. [9] 丁斌, 马海庆. 两级再制造的SM闭环供应链的决策与绩效分析 [J]. 中国管理科学, 2015, 23(6): 118-125. [10] 聂佳佳. 需求信息预测对制造商回收再制造策略的价值 [J]. 管理科学学报, 2014, 17(1): 35-47. [11] 王文宾,邓雯雯. 逆向供应链的政府奖惩机制与税收-补贴机制比较研究 [J]. 中国管理科学,2016,24(4):102-110. [12] 王文宾, 达庆利. 零售商与第三方回收下闭环供应链回收与定价研究 [J]. 管理工程学报, 2010, 24(2): 130-134. [13] 马卫民, 赵璋. 以旧换新补贴对具有不同等级产品闭环供应链的影响研究 [J]. 中国管理科学, 2013, 3(21): 113-117. [14] 曹晓刚, 郑本荣, 闻卉. 考虑顾客偏好的双渠道闭环供应链定价与协调决策 [J]. 中国管理科学, 2015, 23(6): 107-117. [15] Xiong Yu, Zhao Quanwu, Zhou Yu. Manufacturer-remanufacturing vs supplier-remanufacturing in a closed-loop supply chain [J]. International Journal of Production Economics, 2016, 176 (1): 21-28. [16] 陈章跃,王勇,刘华明.考虑顾客策略行为和产品质量的闭环供应链决策模型 [J]. 中国管理科学, 2016,24(3):109-116. [17] Hann I H, Terwiesch C. Measuring the frictional costs of online transactions: The case of a name-your-own-price channel [J]. Management Science, 2003, 49(11):1563-1579. [18] Fay S. Partial-repeat-bidding in the name-your-own-price channel [J]. Marketing Science, 2004, 23(3): 407-418. [19] Terwiesch C, Savin S, Hann I H. Online haggling at a name-your-own-price retailer: Theory and application [J]. Management Science, 2005, 51(3): 339-351. [20] Cai G, Chao Xiuli, Li Jianbin. Optimal reserve prices in name-your-own-price auctions with bidding and channel options [J]. Production and Operations Management, 2009, 18(6): 653-671. [21] Shapiro D. Profitability of the name-your-own-price channel in the case of risk-averse buyers [J]. Marketing Science, 2011, 30(2): 290-304. [22] Chen R R, Gal-Or E, Roma P. Opaque distribution channels for competing service providers: posted price vs. name-your-own-price mechanisms [J]. Operations Research, 2014, 62(4): 733-750. [23] 周振红, 黄深泽. 报价次数对在线报价模式下销售商限制价格的影响 [J]. 系统管理学报, 2011, 20(3): 314-321. [24] Vives X. On the efficiency of Bertrand and Cournot equilibria with product differentiation [J]. Journal of Economic Theory, 1985, 36(1): 166-175. [25] Choi S C. Price competition in a duopoly common retailer channel [J]. Journal of Retailing, 1996, 72(2): 117-134. [27] Bulmus S C, Zhu S X, Teunter R. Competition for cores in remanufacturing [J]. European Journal of Operational Research, 2014, 233(1): 105-113. [28] Wei Jie, Govindan K, Li Yongjian, et al. Pricing and collecting decisions in a closed-loop supply chain with symmetric and asymmetric information [J]. Computers & Operations Research, 2015, 54(2): 257-265. [29] Park J H, MacLachlan D L. Estimating willingness to pay with exaggeration bias-corrected contingent valuation method [J]. Marketing Science, 2008, 27(4): 691-698. [30] Schmidt K M, Spann M, Zeithammer R. Pay what you want as a marketing strategy in monopolistic and competitive markets [J]. Management Science, 2015, 61(6): 1217-1236. Research on Optimal Strategies in a Closed-loop Supply Chain under NYOP and Posted Price Mechanism LI Jian-bin1, ZHU Meng-ping1, DAI Bin2 (1.School of Management, Huazhong University of Science &Technology, Wuhan 430074, China; 2.Economics and Management School, Wuhan University, Wuhan 430072, China) In the recycling and remanufacturing industry, used items are often recycled by a posted price (PP) mechanism. Recently, some online platforms of resource recycling also permit the seller to use the name-your-own-price (NYOP) mechanism, meaning that used items will only be recycled when the bid proposed by the seller is no larger than an opaque reserve price predetermined by the recycling agent. However, in the academic field of closed-loop supply chain, thus far, few researches have been conducted on investigating the NYOP mechanism. In this paper, it's aimed to investigate the optimal strategies in a closed-loop supply chain under three pricing mechanisms: posted price, single-bid NYOP and double-bid NYOP when consumers can additionally propose a second bid if the first bid fails. A Stackelberg game is employed to analyze consumers’ and the manufacturer’s strategies where the latter acts as the leader and the former act as a follower. Based on the nonlinear optimization, the optimal bid for the consumer and the optimal reserve price for the recycling agent under aforementioned three pricing mechanisms are obtained. Furthermore, the optimal strategies among those three pricing mechanisms are compared in terms of profit as well. Result shows that the double-bid mechanism brings about more expected utility for consumers, however, from the perspective of the manufacturer’s profit, the double-bid NYOP mechanism is an inferior strategy. In addition, whether the manufacture adopts the single-bid NYOP mechanism or the posted price mechanism depends on saved cost due to remanufacturing activities and the upper bound of the reserve price. If the upper bound of the reserve price is lower than a certain threshold, as the saved cost increases, the optimal strategy is converted from PP mechanism to the single-bid NYOP mechanism. However, if the upper bound is higher than the threshold, PP mechanism is always the optimal strategy. Moreover, we investigate the effects of key parameters such as the ratio of green consumers on the manufacturer’s profit through numerical studies, and obtain some managerial insights including that the manufacturer should reveal more information such as a lower upper bound of the reserve price to the consumers. Our research enriches the study of consumers’ behavior in the closed-loop supply chain, and provides a reasonable explanation to observations in the recycling industry. These results can also help the manufacturer to choose the optimal pricing mechanism to enhance his profit as well as environmental performance. closed-loop supply chain; remanufacturing; name-your-own-price; posted price 2015-04-20; 2016-01-26 国家自然科学基金资助项目(71571079,71171088,71131004,71301122, 71671133);教育部新世纪人才支持基金(NCET-13-0228);中央高校基本科研业务费(HUST,CXY12M013,武汉大学自主科研项目(人文社科) 简介:戴宾(1983-),男(汉族),湖南人,武汉大学经济与管理学院副教授,研究方向:物流与供应链管理,E-mail:bin_dai@whu.edu.cn. 1003-207(2016)10-0105-12 10.16381/j.cnki.issn1003-207x.2016.10.012 C931 A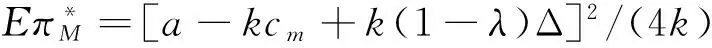
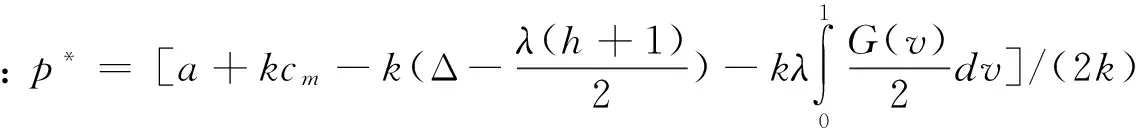







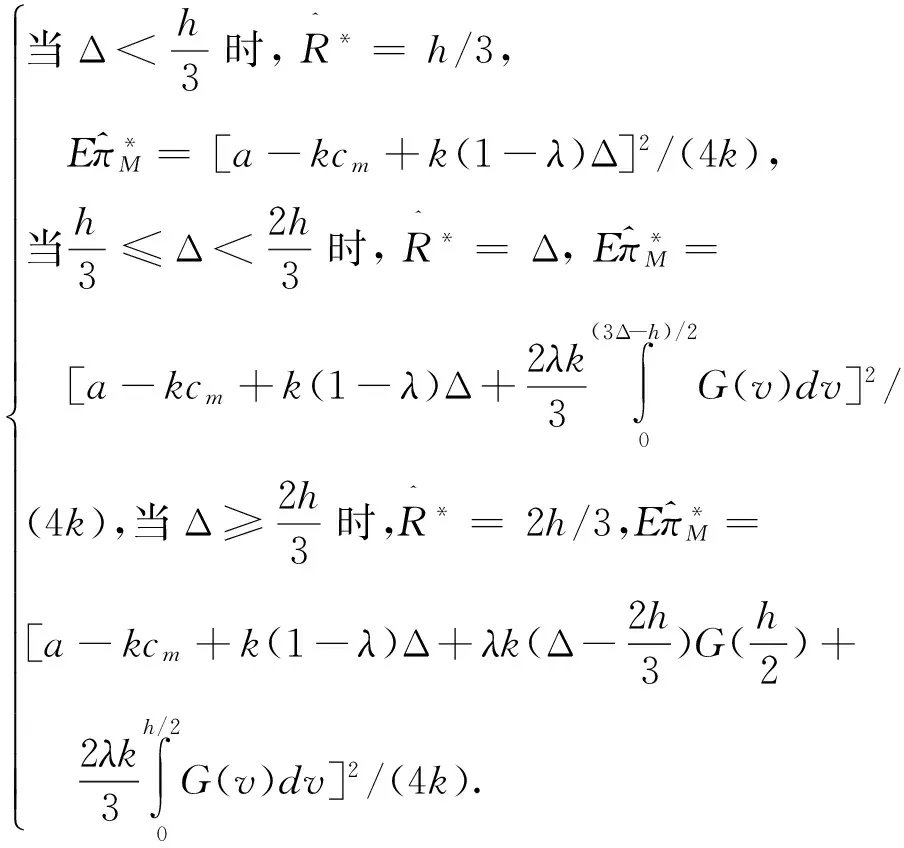

4 固定价格模式

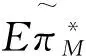
5 回收定价模式比较
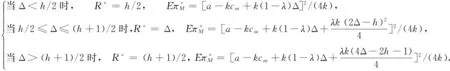

6 算例分析




7 结语