The distribution of deep source rocks in the GS Sag: joint MT–gravity modeling and constrained inversion*

Shi Yan-Ling, Hu Zu-Zhi, Huang Wen-Hui, Wei Qiang, Zhang Sheng, Meng Cui-Xian, and Ji Lian-Sheng

The distribution of deep source rocks in the GS Sag: joint MT–gravity modeling and constrained inversion*

Shi Yan-Ling1,3, Hu Zu-Zhi2,3, Huang Wen-Hui♦1, Wei Qiang3, Zhang Sheng3, Meng Cui-Xian3, and Ji Lian-Sheng3

The coal-bearing strata of the deep Upper Paleozoic in the GS Sag have high hydrocarbon potential. Because of the absence of seismic data, we use electromagnetic (MT) and gravity data jointly to delineate the distribution of deep targets based on well logging and geological data. First, a preliminary geological model is established by using three-dimensional (3D) MT inversion results. Second, using the formation density and gravity anomalies, the preliminary geological model is modified by interactive inversion of the gravity data. Then, we conduct MT-constrained inversion based on the modified model to obtain an optimal geological model until the deviations at all stations are minimized. Finally, the geological model and a seismic profile in the middle of the sag is analysed. We determine that the deep reflections of the seismic profile correspond to the Upper Paleozoic that reaches thickness up to 800 m. The processing of field data suggests that the joint MT–gravity modeling and constrained inversion can reduce the multiple solutions for single geophysical data and thus improve the recognition of deep formations. The MT-constrained inversion is consistent with the geological features in the seismic section. This suggests that the joint MT and gravity modeling and constrained inversion can be used to delineate deep targets in similar basins.

Joint MT–gravity modeling, constrained inversion, deep target

Introduction

The GS Sag is located in the small-to-medium W Basin in the south of the Ordos Basin in central China (Figure 1). The W Basin formed as a rift basin owing to dextral shear stress in the Cenozoic; Cenozoic strata reach thicknesses between 4000 m and 6000 m (Quan, 2005; Xia, 2007). Presently, it is not an exploration target owing to the lack of evidence for large oil or gas reservoirs. The GS Sag has several sets of source–reservoir–cap assemblages but the potentialfor hydrocarbons seems low. Several studies have confirmed the presence of Upper Paleozoic formations (Wang, 1984; Han et al., 2005; Zhang et al., 2001; Li et al., 2011; Yan, 2011). The main evidence for Upper Paleozoic rocks is the following. 1) Upper Paleozoic formations are present in the northern uplift and the southern Qinling Mountains. 2) Carboniferous formations were found in well W3 in the W Basin. Nevertheless, the distribution and thickness of the deep Upper Paleozoic formations is poorly constrained.

Mackie and Madden (1993) proposed 3D MT inversion using the Gauss–Newton method for coarsely parameterized models. Newman and Alumbaugh (2000) used the nonlinear conjugate gradient method and serial and parallel processing for the 3D MT inversion of model data. Hu et al. (2006) proposed a nonlinear conjugate gradient method based on the approximation of the sensitivity matrix, which improved the computational efficiency. The method was used to delineate reservoirs with good results (He et al. 2010b). Lin et al. (2011) studied the 3D conjugate gradient inversion of MT data and Lin et al. (2012) inverted synthetic sparse survey lines.

Owing to the multiple inversion solutions, the interpretation of gravity, magnetic, and electromagnetic data is difficult. Therefore, the joint inversion of various geophysical data has been attempted (Haber and Oldenburg, 1997; Colombo and de Stefano, 2007; Gallardo, 2007; Fregoso and Gallardo, 2009; de Stefano et al., 2011; Moorkamp et al., 2011; Zhdanov et al, 2012; Chen et al., 2012; Gallardo et al., 2012). Haber and Oldenburg (1997) first inverted two different geophysical data sets assuming a common structure. Colombo and de Stefano (2007) used joint inversion of gravity, MT, and seismic data to delineate salt domes by establishing an empirical relation between density, resistivity, and velocity. de Stefano et al. (2010) described an effective method for the joint inversion of multiple-domain geophysical data from the Gulf of Mexico that clearly improved quality. Zhdanov et al. (2012) proposed a new approach to the joint inversion of multimodal geophysical data using Gramian spaces of model parameters and Gramian constraints, computed as determinants of the corresponding Grammian matrices of the multimodal model parameters and their attributes. Yang et al. (2004) studied the joint layerstripped inversion of 3D gravity and seismic data. Chen et al. (2012) achieved good results with the joint inversion of MT and gravity data based on simulated annealing methods. Gallardo et al. (2012) applied cross-gradient joint inversion to marine seismic, MT, gravity, and magnetic data in the continental margin of southeast Brazil. They thus mapped the various units with significant improvements over previous models that were based on processing separate 2D seismic reflections and 2D MT imaging.

Presently, seismic data have high resolution at shallow depths but cannot show the deep complex structure of many exploration areas. Gravity, magnetic, and electromagnetic data complement seismic data. Moreover, to improve the resolution of gravity, magnetic, and electromagnetic interpretations, seismic, geological, and logging data are used to constrain the inversion of gravity, magnetic, and electromagnetic data (Dell’Aversana et al., 2012; Li et al., 2015; Liu et al., 2015). Hu et al. (2010) developed a constrained inversion method of MT data using a parallel simulated annealing algorithm and improved the computational efficiency. Liu (2013) presented a density-constrained 3D gravity inversion method and improved the precision of the prediction of deep salt-dome tops. Hu et al. (2015) proposed a constrained inversion of MT data using the artificial fish swarm optimization method for the precise interpretation of lithology. Presently, there is significant progress in the application of MT and gravity data in studying the lithospheric and crustal electrical structure, and in oil and gas exploration (Nelson et al., 1996; Unsworth et al., 1997; Siripunvaraporn et al., 2004; He et al, 2010a, 2010b, 2015; Nieuwenhuis et al., 2014; Yang et al., 2015; Adetunji et al., 2015). In particularly, these methods facilitate the exploration of complex piedmont, deep targets, and the identification of geological bodies. Li et al. (2012) integrated 3D MT and magnetic and gravity surveys to investigate the lithological variations in conglomerate. Liu et al. (2005) delineated the distribution of deep Carboniferous reservoirs in the Xilin Sag by the joint inversion of gravity and seismic data. Tournerie and Chouteau (2005) used 3D MT surveys to image the structure and stratigraphy of a sedimentary basin; the comparison of the 3D resistivity data with seismic and well logging data suggested that the MT model strongly correlates with the geological structure and stratigraphy. Sun et al. (2007) used 3D MT methods to study complex geological targets in a piedmont zone. The inverted resistivity was consistent with the well logging, and the deep structures were delineated according to the 3D resistivity data. Yu et al. (2008) used joint inversion of MT, seismic, gravity, and magnetic data to study the distribution and basic structural features of Lower Paleozoic strata. Obviously, the joint use of MT, gravity, and seismic data can help understand the distribution and structural characteristics of deep layers.

In the GS Sag, there are several deep 2D seismic profiles of poor quality owing to the surface loess layer. Based on the 3D MT and gravity data, we used joint modeling and constrained inversion of the MT and gravity data to map the deep Upper Paleozoic formations for oil and gas.

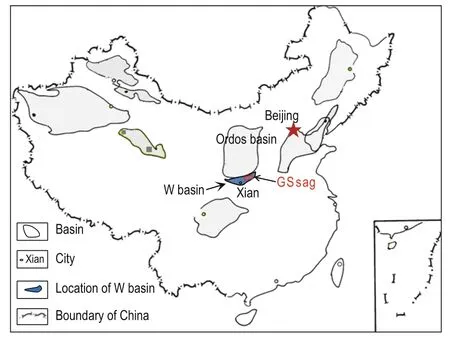
Fig.1 Location of the study area.

Physical analysis

We collected lithology, well logging, and density data from 11 wells in the study area and adjacent areas. We obtained the formation density and the average resistivity, and their variations by using well logging of density and resistivity data at 5 m intervals. The Quaternary strata are mainly loess and loose mudstone, the Neogene strata are sandstone and mudstone, and the deep compacted Paleogene strata are mainly sandstone, sandy mudstone. The Upper Paleozoic is dominated by mudstone and sandy mudstone, whereas the Lower Paleozoic strata are dolomite and limestone.

In Table 1, from top to bottom, the resistivity characteristics of each formation areas follows: ≤15 Ω·m in Quaternary and Cenozoic formations, 30–50 Ω·m in Upper Paleozoic Carboniferous–Permian (C–P) formations, and ＞80 Ω·m in Lower Paleozoic (Pz1) formations. The resistivity difference between Cenozoic and Lower Paleozoic formations is more than four times.

Table 1 Density and resistivity data in the study area

The density characteristics of each formation are the following. The density of the Cenozoic formations is less than 2.37 g/cm3, that of the Upper Paleozoic formations is 2.62 g/cm3, and the density of Pz1 is 2.73 g/cm3. The corresponding density difference is -0.25 g/cm3when there is Upper Paleozoic erathem or -0.36 g/cm3when the Upper Paleozoic erathem is missing. When there are Upper Paleozoic formations, the difference between the Cenozoic and the Upper Paleozoic is the main density interface. The main density interface of the study area is between the Cenozoic and the underlying formations, and the lack of Upper Paleozoic formations strongly affects the gravity anomalies in this area.

In summary, there are obvious differences in the resistivity and density between the Upper Paleozoic and its upper and lower formations.

Joint constrained MT–gravity modeling and inversion

We propose a joint MT–gravity modeling andconstrained inversion technique to delineate the deep Upper Paleozoic strata. The proposed method comprises the following five steps: 1) obtain the resistivity model by 3D MT inversion; 2) interpret the layers in the resistivity model using the physical properties; 3) build a model of the geological structure based on the layer interpretation; 4) invert the model by fitting the gravity data to obtainan optimized model; and 5) obtain the final model by MT-constrained inversion based on the optimized model.

Resistivity model

To obtain high-precision resistivity data, we adopt a 3D inversion method (Hu et al., 2006) to invert the 3D MT data.

The 3D geoelectrical model discrete vector m = [m1, m2, …, mM], the observed data vectorand the error vector; therefore, the classical geophysical problem is represented by the following equation

where F is the forward modeling operator. In the 3D inversion, we choose the one-dimensional sensitivity matrix as the real 3D sensitivity matrix and set all the elements to zero except the element that corresponds to the position of the station

where jkrepresents the position of the k-th station in the jk-th column the of sensitivity matrix, and Nsis the number of stations.

Equation (3) represents the one-dimensional sensitivity matrix of the Ni-th stationwhere Nfis the number of frequencies and φ represents the phase. Using the propagation characteristics of the electromagnetic waves, we propose the following method to obtain the approximate value of the sensitivity elements of nonmeasuring stations.

In equation (4)

where k is a coefficient related to frequency and, where Δxj, Δyj, and Δzjare the distances between the j-th nonmeasuring station and the cuboid unit below the station in the x-, y-, and z-direction.

The computational cost of the sensitivity matrix is high. To minimize the computation time, we use the quasi-Newton method after the first iteration to update the sensitivity matrix as follows (Christiansen and Auken, 2004):

where B is the Broyden matix,and

We found that the CPU time for updating the sensitivity matrix by using the quasi-Newton method is 1/2 to 1/3 less than in the direct calculation. Thus, the method is efficient for the inversion of large amounts of 3D MT data.

The volume effect of the observed MT data is taken into account in the 3D inversion algorithm. All geoelectrical models are involved in the calculation of the electromagnetic field component during the 3D calculation of the model parameters using iterative fitting. This improves the imaging precision of the electrical layer compared to the 2D inversion results and produces high-precision data for stratigraphic interpretations. Figure 2 shows the inverted 3D resistivity data in the study area. The shallow hypro-high resistivity layer represents the Quaternary formations. The blue low-resistivity layer denotes the Cenozoic formations. Under the blue layer in Figure 2, the resistivity is high. The high-resistivity layer shown in light green to yellow-red colors represents the Upper Paleozoic, Lower Paleozoic, and the basement. However, their thicknesses are different. The layer shown in light green and yellowred colors is locally thin and represents the thin Lower Paleozoic formations. When the layer is thick, as in local depressions, it represents the thick Lower Paleozoic formations.

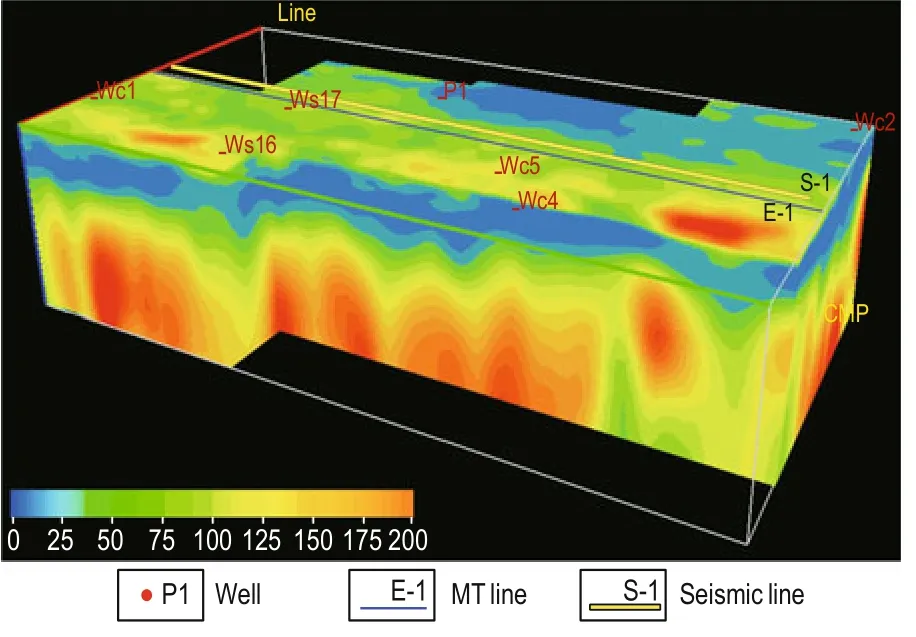
Fig.2 3D resistivity volume of the study area.

Based on the above resistivity model, we used the GeoEast platform in the strata interpretation and produced the electrical resistivity structure of the Upper Paleozoic formations. Figure 3 shows a section of the resistivity data across the line E-1. There is a thick yellow-green resistivity layer buried at greater than 6000 m depth, which represents the Upper Paleozoic formations. The misfits for single MT stations along this profile are 1–10% and greater than 4% between 0 km and 35 km, as shown by the black dotted line in Figure 3b.

Based on the regional geology and data from shallow wells, we obtained the geological model of the resistivity inversion, which is then used as the initial model in the interactive inversion of the gravity data.

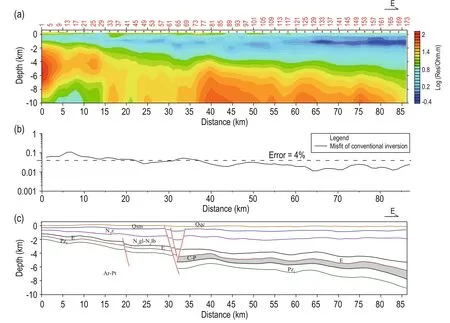
Fig.3 Inversion and interpretation of Line E-1.(a) Resistivity section; (b) Misfit of the MT data; (c) Geological model.

Optimization of the resistivity model using gravity inversion

Despite the good 3D resistivity inversion results, there are nonunique and multiple solutions. We use known physical properties, such as density, to improve the resistivity model, i.e., use gravity data to update the geological model based on the resistivity inversion results only. According to the density data in the study area, the density difference between Cenozoic and Paleozoic generates gravity anomalies. Therefore, the thickness of the Upper Paleozoic formations will directly affect the bottom of the Cenozoic and top of the Lower Paleozoic, and cause gravity anomalies. Thus, the Upper Paleozoic formations can be identified by fitting the gravity data.

The gravity–magnetic–electromagnetic (GeoGME) processing module in the GeoEast software is used in the integrated interactive interpretation. The iterative inversion of the Parker–Oldenburg potential field in the frequency domain is used in the gravity inversion (Parker, 1973, 1974; Oldenburg, 1974). The basic density model is established according to the density values in Table1 based on the interpretation of the previous resistivity profile in Figure 3. In the interactive inversion, the calculated gravity is used to fit the measured gravity data. The misfit is reduced by changing the density model until the desired level is reached. Figure 4 shows the final density model of line E-1. The main steps are the following.

1) Set the layered geological model for the resistivity as the initial model and set a density value for each formation to build the initial density model.

2) Calculate the 3D gravity response over the initial density model to obtain the gravity anomaly and then compare it to the observed gravity anomaly. Find the areas with large anomaly differences in the gravity anomaly map and modify the density of the corresponding area.

3) Modify the density model as follows: First, extract all the 2D sections and models in the areas with the largest gravity anomaly differences between observed and calculated gravity anomalies and then invert the densities interactively. Modify the density of the 2D model on the 2D profiles one by one to fit the observed gravity anomaly curves until the misfit between the calculated and observed gravity anomaly is less than the threshold.

Figure 4 shows the interactive gravity inversion results and misfit curves for line E-1. In this model, the C–P layer is at the west of the line with respect to the initial model in Figure 3c. The thickness and depth of the layers in the section are also modified slightly.

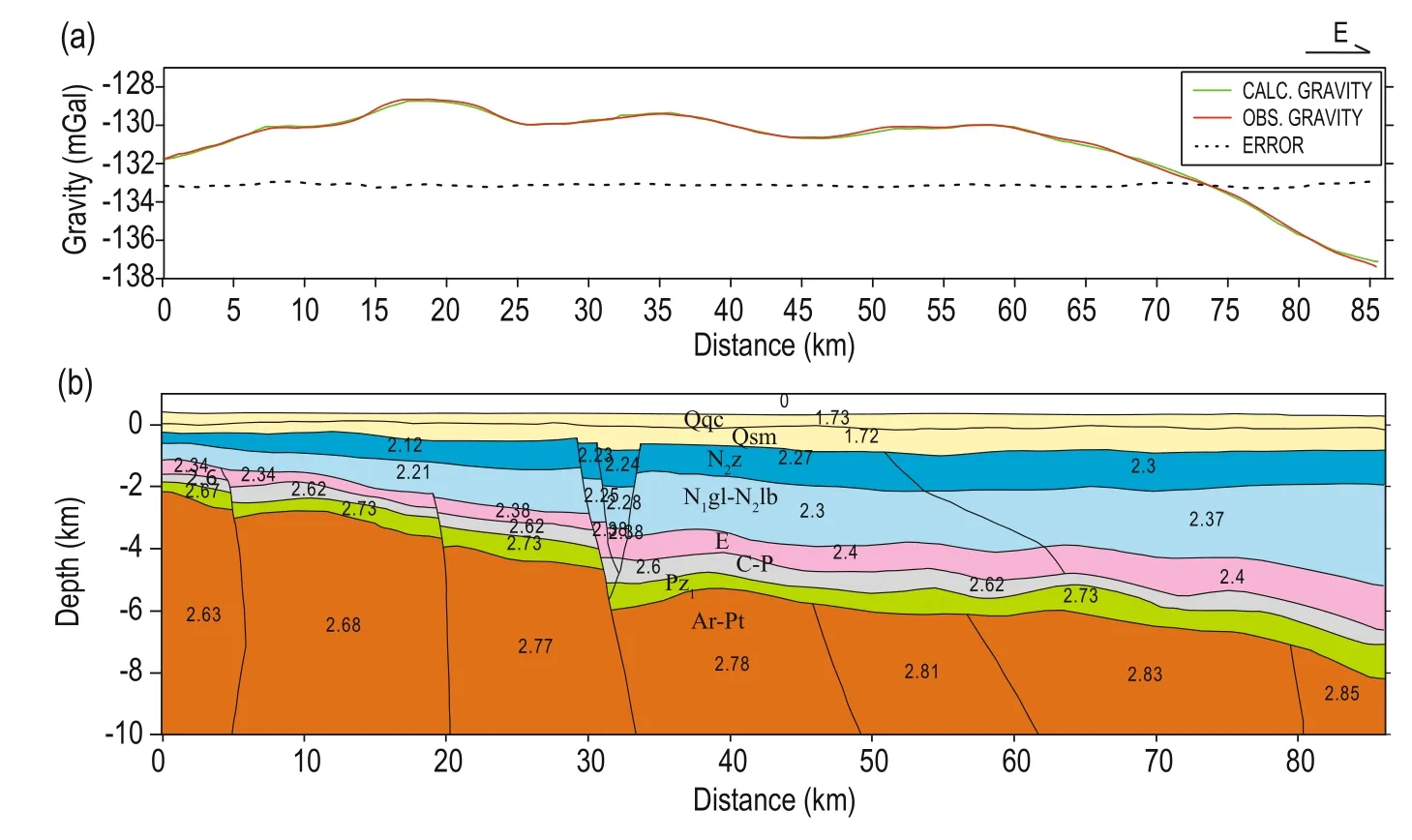
Fig.4 Interactive gravity inversion and misfit curves for line E-1.

Lithology-constrained MT inversion and model optimization

The model is optimized by the interactive gravity inversion. To minimize the nonunique and multiple solutions of the geophysical inversion, we need to use prior information to improve the precision of the processing and interpretation. We use lithologyconstrained MT inversion, in which the prior geological information is used to improve the initial model. The resistivity variation in each layer from electrical logging is given in Table 1 and can be used as prior information in the MT-constrained inversion to optimize the inversion results.

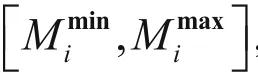
where, mijis the ithparameter of M, miminand mimaxare the low and upper limits of mij, respectively, uiis a random number generated from the uniform distribution between 0 and 1,and Tiis the temperature of ithiteration. From equations (6) and (7), we can find that the modelparameter miis updated in the constrained range [mi, mimax].

The objective function in the lithology-constrained MT inversion is

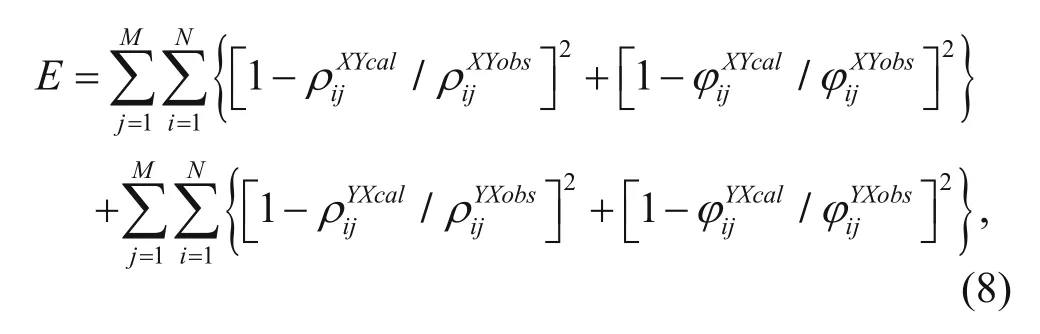
where M is the total MT sounding stations, N is the number of frequencies, ρijXYcal, φijXYcal, ρijYXcal, and φijXYobsare the calculated apparent resistivity and phase of the XY and YX modes, respectively, and ρijXYobs, φijYXcal, ρijYXobs, and φijYXobsare the observed apparent resistivity and phase of the XY and YX modes, respectively.

The inversion steps are the following.

2) The model parameters are modified randomly as Mk+1and we calculate the new objective function

Fig.5 Constrained inversions and geological interpretation of line E-1.

3) Determine whether the change is accepted:

4) Return to step 2) until the objective function E reaches the desired value.

Because the conventional simulated annealing inversion is time-consuming, we use parallel computing to solve this bottleneck (Hu et al., 2010). The optimized resistivity profile is obtained when the constrained inversion of the MT data based on the gravity interactive inversion model is implemented. Taking line E-1 as an example, the processing steps are the following.

1) The resistivity model is established according to the density model in Figure 4b, the formation interfaces are constrained, and the resistivity variation range of each layer is given in Table 1. A new resistivity inversion model is obtained based on the constrained inversion.

2) Calculate and compare the misfits of all stations in the frequency band for the resistivity inversion model and the observed MT data.

3) Based on the deviations, the model is modified in the areas with large deviations and the constrained inversion is used to obtaina new geological model until the deviations at all stations are satisfactory.

Comparing the conventional and constrained inversion profiles, as shown in Figures 3 and 5, the resistivity characteristics of the conventional and constrained inversion are generally consistent in the deep Upper Paleozoic with a secondary high-resistivity region above the basement. After the constrained inversion, the deviations at all MT stations are less than 4% after modifying the C–P distribution. The constrained inversion profile reflects more clearly the boundary of the deep Upper Paleozoic than the conventional inversion, which also confirms the presence of Upper Paleozoic strata. The geological interpretation provides us with a solid base and geophysical evidence for the final determination of the Upper Paleozoic distribution, which is preliminary delineated by the joint MT–gravity modeling and inversion of profile data to plane data. The thickness of the Upper Paleozoic is obtained by the MT-constrained inversion. Then, we finally obtain the thickness distribution of the Upper Paleozoic in the study area, as shown in Figure 6.

Fig.6 Thickness contours of the Upper Paleozoic.

In the study area, the seismic line S-1 is close and parallel to line E-1 in Figure 6. We analyzed the seismic profile of line S-1, as shown in Figure 7. There is a layer beneath the black line (interpreted as the bottom of the Paleozoic) in the central section. The yellow-red layer becomes thick at 30–35 km in the resistivity section of line E-1, where the thickness of the Upper Paleozoic increases.

In addition, the reflection characteristics near traces 6200 and 9300 of the seismic section are consistent with the distribution characteristics of the Upper Paleozoic based on the integrated interpretation of the MT and gravity data. These results suggest that the proposed method canidentify the deep Upper Paleozoic by jointly using MT and gravity modeling and constrained inversion. Clearly, in the exploration of new areas in a basin, joint MT and gravity explorations can be used to obtain information for deep targets and evaluate the oil and gas resources.

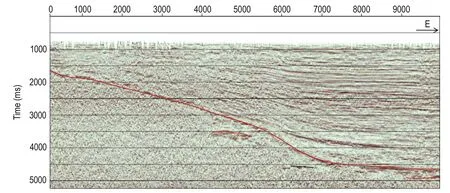
Fig.7 Seismic profile of line S-1.

Regularity and significance of the Upper Paleozoic

Based on the analysis of the potential hydrocarbon resources in the Ordos Basin from the Carboniferous to Permian, Feng et al. (2002) concluded that the hydrocarbons are in coal, dark mudstone, and carbonate rocks. The coal grade is high and anthracite has high gas content of 2.46-23.5 m3/t. Logging data show that the strata thickness is up to 15 m. As the rift basin separated from the Ordos Basin, if the GS Sag has Upper Paleozoic formations, it must have Carboniferous and Permian coal-bearing strata with the same gas productivity. Owing to the high-quality coal beneath the thick Tertiary strata, the coal in the Upper Paleozoic formations is difficult to exploit but it is undoubtedly an important gas resource for the overlying strata (Yan, 2011). Lu et al. (2005) has analyzed the natural gas reservoir conditions of the gas-bearing rocks, the reservoir and cap conditions, the trap conditions, the migration and preservation conditions in the W Basin, and concluded that the W basin has favorable geological conditions for helium.

Based on the joint MT–gravity modeling and constrained inversion, we infer that Upper Paleozoic formations are present in the GS Sag. As shown in Figure 6, the Upper Paleozoic formations are thick estmainly in the deepest eastern and western depressions. In the graben, the thickness of the Upper Paleozoic formations reduces gradually from the deepest site to the slope. In the west of the survey area, the thickness reaches 800 m. In the central and relatively shallow area, the thickness is about 400 m. In the eastern GS Sag, the Upper Paleozoic formations are widely distributed and reach 800 m in thickness. Overall, the Upper Paleozoic formations in the study area cover about 2,300 km2and the area for 400 m thick stratais about 1200 km2.

Conclusions

Based on 3D MT–gravity data, and well logging and geological data, we propose the joint MT–gravity modeling and constrained inversion to map deep targets.

The processing of field data suggests that the joint MT–gravity modeling and constrained inversion can reduce the nonunique and multiple solutions, and thus improve the interpretation of deep formations. The MT-constrained inversion results are consistent with the geological features in the seismic section. This indicated that the joint MT and gravity modeling and constrained inversion can be used to study deep targets.

We use this method to delineate the distribution of deep Upper Paleozoic formations in the GS sag, W Basin. Based on Upper Paleozoic coal-bearing strata in adjacent areas, the estimated hydrocarbon resources of the Upper Paleozoic are deemed significant. Threedimensional MT and gravity exploration are low-cost techniques that can be used to evaluate oil resources in the GS Sag and the W basin and presumably elsewhere.

Acknowledgements

We are grateful to Chief Engineer, He Zhanxiang for his suggestions that assisted in substantially improving the presentation of this paper, and also thanks Zheng Li, and Hao Shujuan in BGP for their help.

Adetunji, A., Ferguson, I. J., and Jones, A.G., 2015, Imaging the mantle lithosphere of the Precambrian Grenville Province: large-scale electrical resistivity structures: Geophysical Journal International, 201, 1038–1059.

Chen, H. G., Li, J. X., Wu, J. S., and Yu, P., 2012, Study on simulated-annealing MT-gravity joint inversion: Chinese J. Geophys. (in Chinese), 55(2), 663–670.

Christiansen, A. V., and Auken, E., 2004, Optimizing a layered and laterally constrained 2D inversion of resistivity data using Broyden’s update and 1D derivatives: J. Appl. Geophys., 56, 247–261.

Colombo, D., and De Stefano, M., 2007, Geophysical modeling via simultaneous joint inversion of seiemic, gravity, and electromagnetic data: Application to prestack depth imaging: The Leading Edge, 26(3), 326–331.

Dell'Aversana, P., Colombo, S., Ciurlo, B., Leutscher, J., and Seldal, J., 2012, CSEM data interpretation constrained by seismic and gravity data: An application in a complex geological setting: First Break, 30(11), 43–52.

de Stefano, M., Andreasi, F. G., Re, S., Virgilioet, M., and Snyder, F. F., 2011, Multiple–domain, simultaneous jointinversion of geophysical data with application to subsalt imaging: Geophysics, 76(3), R69–R80.

Feng, S. L., Ye, J. P., and Zhang, S. A., 2002, Coalbed methane resources in the Ordos Basin and its development potential: Geological Bulletin of China (in Chinese),21(10), 658–662.

Fregoso, E., and Gallardo, L. A., 2009, Cross–gradients joint 3D inversion with applications to gravity and magnetic data: Geophysics, 74(4), L31–L42.

Gallardo, L. A., 2007, Multiple cross–gradient joint inversion for geospectral imaging: Geophys. Res. Lett., 34(19), L19301.

Gallardo, L. A., Fontes, S. L., Meju, M. A., Buonora, M. P., and de Lugao, P. P., 2012, Robust geophysical integration through structure–coupled joint inversion and multispectral fusion of seismic reflection, magnetotelluric, magnetic and gravity images: example from Santos Basin, offshore Brazil: Geophysics, 77(5), B237–B251.

Haber, E., and Oldenburg, D., 1997, Joint inversion: A structural approach: Inverse Problems, 13(1), 63–77.

Han, H. Y., Zhang, Y., and Yuan, Z. X., 2005, The formation and evolution of W basin and the movement of the fault blocks: Earthquake Rresearch (in Chinese), 25(4), 362–368.

He, Z. X., Hu, W. B., and Dong, W. B., 2010a, Petroleum EM prospecting advances and case studies in China: Surveys in Geophysics, 31(2), 207–224.

He, Z. X., Hu, Z. Z., Gao, Y., He, L. F., Meng, C. X., and Yang, L. K., 2015, Field test of monitoring gas reservoir development using timelapse continuous electromagnetic profile method: Geophysics, 80(2), WA127–WA134.

He, Z. X., Hu, Z. Z., Luo, W. F., and Wang, C. F., 2010b, Mapping reservoirs based on induced polarization and Resistivity anomaly of continuous 3D electromagnetic profiling: Case study from Qaidam Basin, China: Geophysics, 75(1) , 25–33.

Hu, Z. Z., He, Z. X., Wang, Y. T., and Sun, W. B., 2010, MT parallel simulated annealing constrained inversion and its application: 80th Annual International Meeting, SEG Expanded Abstracts, 895–899.

Hu, Z. Z., He, Z. X., Yang, W. C., and Hu, X. Y., 2015, Constrained inversion of magnetotelluric data with the artificial fish swarm optimization method: Chinese J. Geophys. (in Chinese), 58(7), 2578–2587.

Hu, Z. Z., Hu, X. Y., and He, Z. X., 2006, Pseudo-Three-Dimensional magneto-telluric inversion using nonlinear conjugate gradients: Chinese J. Geophys, 49, 1226–1234.

Li, D. C., Yang, S. J., and Hu, Z. Z., Zhao, Z., Li, Y., Zhong, D. K., Sun, W. B., and Ji, L. S., 2012, Joint interpretation of 3D Gravity-magnetic and seismic data: Oil Geophysical Prospecting (in Chinese), 47(2), 353–359.

Li, S. C., Nie, L. C., Liu, B., Song, J., Liu, Z. Y., Su, M. X., Xu, L., and Sun, H. F., 2015, 3D electrical resistivity inversion using prior spatial shape constraints: Applied Geophysics, 10(4), 361–372.

Li, Y. H., Li, J. C., Li, J. C., Chen, G. C., Wei, X. Y., and Xu, H. H., 2011, Genetic and significance of natural gas in W basin: Journal of Xi’an Shiyou University (in Chinese), 26(5), 11–18.

Lin, C. H., Tan, H. D., Shu, Q., Tong, T., and Zhang, Y. M., 2012, Three-dimensional interpretation of sparse survey line MT data: synthetic examples: Applied Geophysics, 9(1), 9–18.

Lin, C. H., Tan, H. D., and Tong, T., 2011, Threedimensional conjugate gradient inversion of magnetotelluric full information data: Applied Geophysics, 8(1), 1–10.

Liu, J. C., Liu, L. T., Liang, X. H., and Ye, Z. R., 2015, 3D density inversion of gravity gradient data using the extrapolated Tikhonov regularization: Applied Geophysics, 12(2), 137–146.

Liu, T. Y., Yang, Y. S., and Li, Y. Y., 2005, Deciding on the distribution of deep reservoir by the joint inversion method of gravity and seismic data-taking the carboniferous in Xilin sag as an example: Natural Gas Industry (in Chinese), 25(5), 34–36.

Liu, Y. X., 2013, Application of a three-dimensional gravity inversion method constrained with density in complex areas: 83rd Annual International Meeting, SEG Expanded Abstracts, 1156–1160.

Lu, J. C., Wei, X. X., and Li, Y. H., 2005, Preliminary study about genesis and pool formation conditions of rich-helium type natural gas: Northwest Geology (in Chinese), 38(3), 82–86.

Mackie, R. L., and Madden, T. R., 1993, Three-dimensional magnetotelluric inversion using conjugate gradients: Geophysical Journal International, 115, 215–229.

Moorkamp, M., Heincke, B., Jegen, M., Roberts, A. W., and Hobbs, R. W., 2011, A framework for 3-D joint inversion of MT, gravity andseismic refraction data: Geophysical Journal International, 184(1), 477–493.

Nelson, K.D., Zhao, W. J., Brown, L. D., et al., 1996, Partially molten middle crust beneath southern Tibet: an initial synthesis of Project INDEPTH results: Science, 274, 1684–1688.

Newman, G. A. and Alumbaugh, D. L., 2000, Threedimensional magnetotelluric inversion using non-linear conjugate gradients: Geophysical Journal International, 140, 410–424.

Nieuwenhuis, G., Unsworth, M. J., Pana, D., Craven, J., and Bertrand, E., 2014, Three-dimensional resistivity structure of Southern Alberta, Canada: implications for Precambrian tectonics: Geophysical Journal International, 197, 838–859

Oldenburg, D. W., 1974, The inversion and interpretation of gravity anomalies: Geophysics, 39(4), 526–536.

Parker, R. L., 1973, The rapid calculation of potential anomalies: Geophysical Journal of the RoyalAstronomical Society, 31(4), 447–455.

Parker, R. L., 1974, Best bounds on density and depth from gravity data: Geophysics, 39(5), 644–649.

Quan, X. C., 2005, Study on fracture structure of W Basin: China Coal geology (in Chinese), 17(3), 1–5.

Siripunvaraporn, W., Uyeshima, M., and Egbert, G., 2004, Three–dimensional inversion for network–magnetotelluric data: Earth Planets Space, 56(9), 893–902.

Sun, W. B., Deng, Y. Y., Wang, C. F., Hu, Z. Z., and Lin, C. G., 2007, Deep structure study in complex area by 3D MT Data: 77th Annual International Meeting, SEG Expanded Abstracts, 684–687.

Tournerie, B., and Chouteau, M., 2005, Three-dimensional magnetotelluric survey to image structure and stratigraphy of a sedimentary basin in Hungary: Physics of the Earth and Planetary Interiors, 150, 197–212.

Unsworth, M. J., Malin, P., Egbert, G. D., and Booker, J. R., 1997, Internal structure of the San Andreas fault at Parkfield, California: Geology, 25, 359–362.

Wang, J. M., 1984, A study on the tectonics of the Weihe river graben: Geological Review (in Chinese), 30(3), 217–223.

Xia,Y., 2007, The relationship between the sedimentary characteristics of the Cenozoic and structure in W basin: Master's thesis, Chang'an University, Xi'an.

Yan, J. P., 2011, Sedimentary-tectonic evolution and gaspotential exploration of Late Paleozoic in Southern Ordos Basin: PhD Thesis, Northwest University, Xi'an.

Yang, H., Dai, S. K., and Mu, Y. G., 2004, Joint layerstripped inversion of 3-D gravity and seismic data: Oil Geophysical Prospecting (in Chinese), 39(4), 468–471.

Yang, W. C., Xu, Y. X., Zhang, L. L., Yu, C. Q., Yu, P., Zhang, B. Z., and Yang, B., 2015, Magnetotellruic investigation and 3D lithospheric structures in the Tarim terrane: Acta Geologica Sinica (in Chinese), 89(7), 1151–1161.

Yu, P., Zhang, L. L., Wang, J. L., and Wu, J. S., 2008, Determination of physical property parameters structure in middle Guizhou uplift by joint inversion of magnetotelluric, seismic, gravity and magnetic data: Journal of Tongji University (Nature Science) (in Chinese), 36(3), 406–412.

Zhang, G. W., Zhang, B. R., Yuan, X. C., et al., 2001, Qinling Orogenic belt and continental dynamics: Science Press, Beijing.

Zhdanov, M. S., Gribenko, A., and Wilson, G., 2012, Generalized joint inversion of multimodal geophysical data using Gramian constraints: Geophys. Res. Lett., 39, L09301.

Shi Yan-Ling graduated from the School of Earth Sciences, China University of Geosciences (Wuhan) and then received her MSc in 2011. Presently, she is a PhD student at China University of Geosciences (Beijing). She is interested in the exploration of oil-bearing basins.

Manuscript received by the Editor August 20, 2015; revised manuscript received July 15, 2016.

*This work was supported by the National Science and Technology Major Project (No. 2016ZX05018006), the National Key Research Development Program (No. 2016YFC0601104), and the National Natural Science Foundation of China (No. 41472136).

1. School of Energy Resources, China University of Geosciences, Beijing 100083, China.

2. Institute of Geophysics & Geomatics, China University of Geosciences, Wuhan 430074, China.

3. BGP, CNPC, Zhuozhou 072751, China.

♦Correspondence author: Huang Wen-Hui (Email: huangwh@cugb.edu.cn)

© 2016 The Editorial Department of APPLIED GEOPHYSICS. All rights reserved.