带电薄圆环片电场的空间分布

江俊勤

(广东第二师范学院 物理系，广东 广州 510303)



带电薄圆环片电场的空间分布

江俊勤

(广东第二师范学院 物理系，广东 广州 510303)

用叠加原理和数值分析法，利用Methmetica强劲的解析计算能力和卓越的数字绘图功能，对均匀带电薄圆环片的电场进行全面的研究，绘制出电场强度的空间分布图．

带电薄圆环片;电场强度;叠加原理;椭圆积分;数字绘图

带电细圆环、薄圆盘以及薄圆环片的电势及电场强度是电磁场理论教学的重要问题，现行教科书或题解以及教学研究文献有许多讨论，尽管各文献所用方法各异[1-4]，但最终都是把电势表达为以勒让德多项式为基的级数解(以下简称为勒让德级数解). 从理论上讲，有了电势的勒让德级数解，通过计算电势的梯度，就可以计算出电场强度，文献[4]也具体给出了电场强度的勒让德级数解.

然而，如何从电势及电场强度的让德级数解出发具体计算出这些带电系统的电场？电场的空间分布图如何？ 到目前为止，未见有其他作者进行过这项工作.

为了回答这些问题，笔者使用著名软件Mathematica对带电细圆环、薄圆盘以及薄圆环片的电势和电场强度的空间分布图进行计算和绘制.研究结果表明：

(1)电势的勒让德级数解收敛比较快，只需计算到前几十项(对于薄圆盘以及薄圆环片，只需计算到前19项即36阶勒让德多项式)，就可绘制出正确的空间分布图.

(2)电场强度的勒让德级数解收敛极其缓慢. 对于带电细圆环，计算至勒让德级数的前231项(即460阶勒让德多项式，计算机运行一个多小时),才能得到正确的结果[5];特别是对于薄圆盘以及薄圆环片的勒让德级数解收敛更缓慢，很难用它计算和绘制出电场的空间分布——计算至级数的前301项(即第600阶勒让德多项式),计算机花费了长达2小时45分的时间仍然未到达收敛!——在较接近圆盘的区域,由Mathematica绘制出电场强度的空间分布图仍是不正确的.

因此寻找其他方法研究带电细圆环和薄圆环(薄圆盘)片电场强度的空间分布，对于电磁场教学具有积极的意义.文献从点电荷电场强度公式出发，用叠加原理研究了均匀带电细圆环电场强度的空间分布[6]；文献从点电荷电势公式出发，用叠加原理研究了均匀带电薄圆盘和薄宽圆环电势的空间分布[7].

本文发展了文献[6]和[7]的方法，进一步利用著名软件Mathematica强劲的解析计算能力和的数字绘图功能，特别是Mathematica中关于椭圆积分运算的杰出性能，用点电荷电势公式和叠加原理对带电薄圆环片的电场进行数值研究、绘制电场强度大小和方向的空间分布图．

1 均匀带薄圆环片的电势和电场强度的积分表达式

考虑一个外半径为a，内半径为b的均匀带电薄圆环片(当b→0时对应于薄圆盘)，所带电荷为Q(正电荷)，以圆环心O为坐标原点，z轴垂直于圆盘所在平面，如图1所示．

考虑薄圆环片上的任一个面元ds，坐标为(ρcosφ，ρsinφ，0)，设电荷均匀分布于薄圆环片,则面元上ds=ρdρdφ的电荷为

观测点P的坐标为(x,y,z)，P到面元ds的距离为

(1)

电势是标量，根据叠加原理只需把各个电荷元(点电荷)的电势直接累加就是总电势了, 所以空间任意观测点P(x,y,z)处的电势为

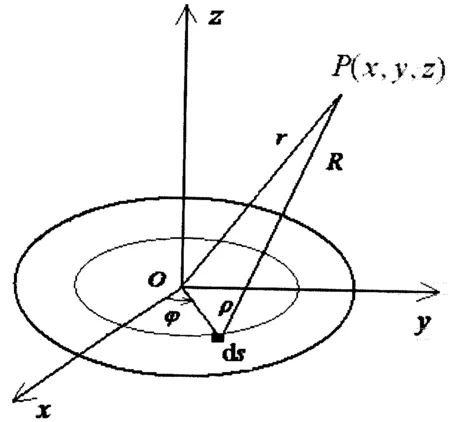
图1 带电薄圆环片与坐标系

由于具有轴对称性，故只需研究xoz平面内的观测点P(x,0,z)处的电场，它代表了任意经过oz轴的平面内的电场分布. 这样，电势积分计算式可简化为：

(2)

若记

(3)

则

(4)

(5)

式(3)可以用第一类完全椭圆积分表示，经计算得

(6)

由式(4)-式(6), 通过对椭圆积分求梯度可以获得电场强度. 这些计算的自动快速实现得益于Mathematica强大的解析计算能力，特别是关于椭圆积分运算的杰出性能.

2 均匀带薄圆环片电场强度的数值结果

为了计算的方便，以a作为x和z的单位，以U0=Q/(4π2ε0a)为电势的单位、以E0=Q/(4π2ε0a2)为电场强度的单位.并取b=1/2和a=1，根据式(4)-式(6)，应用Mathematica的标准数值积分法和数字绘图功能，可以研究均匀带电薄圆环片激发的电场强度的量值和方向的分布.

图2 均匀带电圆环片电势的空间分布

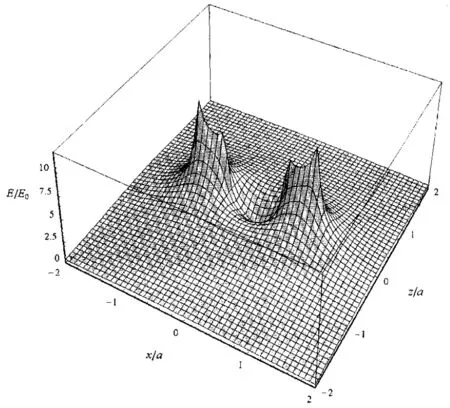
图3 均匀带电圆环片电场强度大小的空间分布

图4 均匀带电圆环片电场强度方向与等势线分布图

显然当x≫a或z≫a时，带电薄圆环片激发的电场类似于点电荷的电场，即电场主要分布在圆环片附近.取研究范围为-2≤x≤2和-2≤z≤2，由于采用了电荷面分布模型，讨论带电薄圆环片上的电场强度是没有意义的，所以电场强度的研究分z<0和z>0两个区域进行，在实际的数值计算中，这两个研究区域的具体取值为-2≤z≤-0.002和0.002≤z≤2.

数值结果是：电势分布如图2所示，电场强度大小的分布如图3所示，电场方向的分布图和等势线分布则如图4所示.

由图2可知,在圆环片上内外半径之间出现电势峰值.由图3可知,在圆环片外边缘附近电场强度最大(主峰)，圆环片内边缘附近也形成一个场强次高峰;圆心附近则是一个低谷，圆心处场强为零，主峰与次峰之间是圆环状的沟;由于0.002与0很接近，所以图3中没有明显表现出两个区域的间断，只是在z=0处的那条网格线变粗了一点点(如果取两个研究区域为-2≤z≤-0.001和0.001≤z≤2，结果也是一样的).

图4显示：电场方向处处与等势线垂直，这是理所当然的结果了.

3 结论

本文用叠加原理和数值分析方法，利用Mathematica卓越的解析计算能力和强劲的数字绘图功能，特别是Mathematica中关于椭圆积分运算的杰出性能，对均匀带电薄圆环片的电场强度进行全面的研究，绘制了电场强度的空间分布图(按作者所知，这是第一次给出真正的空间分布图).本文的结果不但可以充实教学内容，而且有助于人们理解和掌握该电场的分布规律. 本文的方法为电磁场数字化研究提供了一种有效的途径：物理原理和计算方法简单易懂、计算和绘图快速、结果准确而且形象直观.

[1] 杰克逊J D．经典电动力学(上册)[M]．朱培豫，译．北京：高等教育出版社，1978:102,143.

[2] 林璇英，张之翔．电动力学题解(第二版)[M].北京：科学出版社，2007：146-157.

[3] 吴崇试．均匀带电薄圆盘的电势问题[J]．大学物理,2000,19(11)：1-4.

[4] 贾秀敏．均匀带电圆环片的空间静电场[J]．大学物理,2010,29(8)：29-30.

[5] 江俊勤.带电圆线圈静电场勒让德级数解的收敛速度[J]．广东第二师范学院学报：自然科学版，2013，33(10)：46-50.

[6] 江俊勤.也谈均匀带电细圆环电场的分布[J]．大学物理,2007,26(11)：39-42.

[7] 江俊勤.均匀带电薄圆盘和薄宽圆环静电势的数值研究[J]．广东第二师范学院学报：自然科学版，2011，31(3)：31-33.

Spatial Distribution of Electric Field from a Charged Round Ring Slice

JIANG Jun-qin

(Department of Physics, Guangdong University of Education, Guangzhou 510303, China)

Based on the superposition principle, the electrostatic field of a uniformly charged round ring slice was numerically investigated by using the Mathematica with the strong analytical computing power and the excellent digital drawing function. The spatial distribution diagrams of the electric field are plotted.

charged round ring slice; electric field; superposition principle; elliptic integral; digital drawing

2015-05-06

广东省高等学校物理专业综合改革试点项目(9010-14246).

江俊勤(1962-)，男，广东揭阳人，广东第二师范学院物理系教授，从事理论物理教学和格点规范理论的研究工作，所发表论文中有27篇被SCI收录，其中在Physical Review D上4篇.

10.14182/J.cnki.1001-2443.2016.05.006

O441.1

A

1001-2443(2016)05-0434-03