部分交代谢修正

袁永锋

（南京大学哲学系，江苏南京210023）

【逻辑学研究】

部分交代谢修正

袁永锋

（南京大学哲学系，江苏南京210023）

代谢修正是信念修正中一种常见的非优先复合修正。在部分交代谢修正过程中，认知主体往往先接受所有新信息为新信念；然后在后续认知过程中发现信念冲突，并借助核心信念来形成若干竞争性候选理论；最后通过这些候选理论来发现和放弃不可信信息，进而化解信念冲突，并同时保护核心信念。它的公理性假定与函数式构造之间具有信念修正领域的“完全性定理”，即表达定理。

信念修正；部分交代谢修正；核心信念；保留集

［栏目主持人］北京大学哲学系陈波教授

［主持人语］本期发表两篇逻辑技术性很强的论文，它们都借助当代逻辑学与其他领域交叉的某种前沿理论去处理某个具体问题，获得某种形式化的结果，并着眼于计算机科学中的知识表示和知识推理。这种研究方式值得提倡和肯定。袁永锋的论文讨论部分交代谢修正——一种先膨胀后巩固并同时保护理论硬核的信念修正过程。该文采用AGM研究范式先对它做公理性刻画，并通过“候选理论”和“核心信念”这两个概念来分析阐述认知主体对不可信信息的发现与清除，进而给出了基于保留集的函数式构造，最后证明了公理性假定和函数式构造这两种形式刻画方式之间的等价性，表明了部分交代谢修正算子具有形式上的“完全性”。张晓君、李晟的论文利用广义量词理论所揭示的四个亚里斯多德量词的单调性之间的转换关系，根据AAA-1和EAE-1这两个显而易见的公理，推出了亚里斯多德三段论的全部24个有效式。

信念修正（belief revision）理论是利用符号逻辑的方法来刻画认知主体信念状态的理性改变的研究领域。它是一个涉及逻辑学、形式认识论、哲学和人工智能等学科的交叉领域。自从1985年阿尔科荣（C. E.Alchourrón）、加邓福斯（P.Gärdenfors）和麦金森（D.Makinson）在[1]中确立了信念修正理论的AGM研究范式以来，信念修正理论形成了各种各样的研究分支（参阅[2][3]）。其中非优先复合修正理论是最新学术前沿，研究文献相对较少。近两年袁永锋等人对这一主题进行了系统研究。袁永锋和鞠实儿在[4]中首先提出并刻画了理性评价机制。袁永锋、鞠实儿和文学锋在[5]中刻画了以评价结果为新信息的评价复合修正。这两篇文章分别实现了决策-修正模式（参见[6]）的决策模块和修正模块。此外，袁永锋在[7]中提出并刻画了基于核心集（kernel set）概念的核心代谢修正算子。它的直观动机是说：“如果（由于有限理性的缘故）认知主体并不能立刻从新信息中区分出不可信信息，那么他通常会先将这些新信息都作为新信念添加进信念库中；然后在后续的认知过程中，他可能会因信念冲突现象的出现而发现并放弃不可信信息”。这采用的是汉森（S.O.Hansson）在[6]中提出的另一种信念修正模式，即膨胀-巩固模式。此模式的膨胀模块仅是对旧信念库和新信息的集合并运算，巩固模块则需要从这个并集中剔除不可信信息，以化解信念冲突。但在巩固过程中，理性主体并不是同等对待所有这些信息，有一些可靠无疑的信念会被用来确定可疑信念的范围，并且它们同时会受到认知主体的有意的保护。鉴于此，这里将采用一种基于保留集（remainder set）概念的构造方法，来刻画这种受可靠信念所影响的内部认知机制，即部分交代谢修正。

一、公理性刻画

本文采用小写希腊字母（如α，β，φ，ψ等）表示命题语言L中的命题，用⊥表示任意矛盾式，用大写拉丁字母（如A，B，C，D等）表示L中的命题集，用Cn和├表示逻辑后承，用P（S）表示S的幂集。在刻画部分交代谢修正之前，先来看下面这个部分交代谢修正的例子。

例子1物理学家费教授相信某物理学理论体系B，尤其是其核心部分A。有一次，他的同事根据最新实验数据提出了假说D。费教授认为D也是符合直观的，跟理论体系B并无冲突，也没有明显不可信的信息。因此，他相信了假说D。但在后续理论研究中，他发现B和D在某个细节上是相互矛盾的。这种矛盾现象导致无法同时相信命题φ和ψ。如果相信命题φ，那么会形成一个反对ψ的理论T1；如果相信命题ψ，那么会形成一个反对φ的竞争性理论T2。此时他可以随意地支持某个理论即可。但由于这两个命题都受到相应理论的反对，他为慎重考虑，认为两者都有错误的嫌疑，从而都不相信。并且也不再相信支持这二者的部分相关命题，而只相信这两个竞争理论（T1和T2）都赞同或支持的那些命题，从而提出了新的理论体系B′。新体系B′并没有全盘否定B，依然保留了B理论中的一些可靠的核心内容A，同样B′也没有完全否定D假说，而是放弃了一些与A相冲突的不可信信息。

这个例子表明，当认知主体不能及时从新信息中区分出不可信信息时，他往往会相信这些新信息。但这种相信可能会导致信念状态的（潜藏的）不一致性。因此，在后续认知过程中，他可能会碰到信念冲突而发现不可信的信息，并将它们清除出去以化解信念冲突。虽然这种“发现”与“清除”是主观的认知行动，但也往往有理性规则可循。在遇到信念冲突时，认知主体往往会徘徊于相信哪个相关命题，从而形成若干具有竞争关系的候选理论，并通过它们进行分析和决策。如果只形成一个候选理论，那么认知主体会直接相信这个候选理论。但如果形成两个及以上的候选理论，那么认知主体往往会对那些被若干候选理论所反对的命题产生怀疑，进而只相信那些所有候选理论都赞同、支持的命题。那么候选理论是否是任意形成的呢？答案自然是否定的。只有满足某些理性条件的候选理论，认知主体才会认为它是具有竞争性的。显然，候选理论应当满足一致性。除此以外，最自然的条件就是信念的可靠性，只有包含可靠信念的理论才具有作为候选理论的资格。这种可靠信念与其他信念的不同之处在于，认知主体认为他们能对它们作出足够强的辩护，并且确信这些信念是千真万确的。正如舒卓和朱菁在[8]中所显示的那般，信念可以粗略分为两类：一类是为避免错误而坚守克利福德原则形成的具有证据支持和合理辩护的可靠信念，另一类是为避免错失真理而放宽信念门槛形成的尚无决定性证据支持的其他信念。比如，例1中费教授的可靠信念A和其他信念。这种可靠信念也就是[4]和[5]中考察的那种核心信念（core beliefs）。对核心信念和其他信念的区分甚至可以追溯到科学哲学家拉卡托斯（I.Lakatos）。他的科学研究纲领理论（参阅[9]）区分了科学理论的硬核（hard core）和辅助假设（auxiliary hypotheses）。在遭遇反常事实时，科学家往往不会轻易地触动理论的硬核，而是通过调整硬核的保护带——辅助假设来化解理论危机。麦金森在[10]中也对核心信念和非核心信念作出了区分，他把核心信念看作是极其神圣而不可改变的。综上所述，在部分交代谢修正时，为了解决信念冲突，必须放弃部分信念以恢复信念状态的一致性；但并不是随意地放弃信念，核心信念或理论硬核会通过候选理论来影响信念修正过程，并同时得到保护。

从例1可知，部分交代谢修正具有新信息、信念状态（或理论体系）和部分交代谢修正算子这三个组件。对于新信息，本文用命题集来表征（如D）。对于信念状态，由于要考虑信念库中的核心信念，故这里采用下面这个形式概念来表征。

定义1[5]一个信念状态（B，A）是一个满足下列条件的二元组：

（1）A⊆B⊆L，（2）A是一致的，（3）A是相对于B逻辑封闭的，即Cn（A）∩B⊆A。

对于部分交代谢修正算子，本文用◇来表示。它是一个基于信念状态（B，A）并以新信息D作为输入的算子，它的输出是一个新的信念状态（B，A）◇D。（B，A）◇D仍然是一个二元组，本文用B◇AD和A◇BD分别表示新信念状态的信念库和核心信念集。

那么如何修正才是理性的部分交代谢修正呢？袁永锋在[7]中认为应当遵循三个原则，即极小改变原则（或者说极大效用原则）、一致性原则和保护性原则。根据这三个指导原则，下面给出◇的一些合理的公理性假定。对于所有的D，D1，D2⊆L，

其中，前七条公理性假定引用自[7]，下面简单说明它们的直观思想，以便于理解。M-BelState：修正结果（B，A）◇D是一个信念状态。M-CoreInvariance：修正前后的核心信念集是逻辑等价的，因为由M-CoreInvariance易证Cn（A◇BD）=Cn（A）。M-Inclusion：新信念库里的信念只来源于旧信念库或新信息。M-Protection：认知主体会有意地保护核心信念，而不会随意地放弃这些他们坚信的“理论硬核”。M-Consistency：经过巩固的信念状态应该是稳定的、协调的，故可以合理地要求新信念库满足一致性。M-RelClosure：新信念库里的信息对认知主体而言都是可信的；如果这些可信信息的某些逻辑后承在B∪D里但却没有在修正过程中保留下来，那么这种信念修正是不理性的。M-Vacuity：如果B∪D是一致的，那么认知主体在巩固时无法从B∪D中区分出不可信信息；根据极大效用原则，不需要从B∪D中放弃任何信息，即新信念库应包含B∪D中的所有信息。最后两条公理性假定刻画的是部分交代谢修正的独特性质。M-Irrelevance的直观涵义是说：如果信念库B分别与两新信息的并集的交集外信息都是矛盾式，那么这些交集外信息都是不可信的，都应当在修正过程中被删除；因此，保留下来的可信信息只与该交集相关，从而最终这两个新信念库应该相等。M-Relevance从两方面作出要求：每一个被放弃的不可信信息都不仅不能是核心信念集A的逻辑后承，而且必须在某种意义上是不可信的信念。第一个要求使得核心信念得到保护。第二个要求的直观意思是说：能够在B∪D范围内找到一个一致子集对被放弃的ψ构成反驳；并且提供这种反驳的这个一致子集必须以认知主体所认为的可信信息B◇AD作为基础。

上述这些公理性假定并不都是相互独立的，它们具有下列相互关系。

命题1令（B，A）∈B。

（1）M-Relevance⇒M-Protection。

（2）M-Relevance⇒M-Vacuity。

（3）M-Relevance⇒M-RelClosure。

（4）M-BelState+M-CoreInvariance⇒M-Protection。

证明：（1）、（2）和（4）易证，略。

（3）令◇满足M-Relevance。用反证法，假设Cn（B◇AD）∩（B∪D）B◇AD，故存在ψ∈（B∪D）B◇AD使得B◇AD├ψ。由ψ∈（B∪D）B◇AD和M-Relevance知：存在C⊆B∪D使得B◇AD⊆C且C⊥但C∪{ψ}├⊥。由于B◇AD⊆C且B◇AD├ψ，故C├ψ，故Cn（C）=Cn（C∪{ψ}）。这与C⊥且C∪{ψ}├⊥产生矛盾，故假设错误，M-RelClosure成立。

二、函数式构造

本节将给出部分交代谢修正算子◇的函数式构造。根据极大效用原则、一致性原则和上面对例1的分析阐述易知，这里需要构造极大一致的候选理论，故采用阿尔科荣等提出的保留集概念来构造。

定义2[11]125～148令B，C⊆L。X∈B▽C当且仅当X满足下列条件：

（1）X⊆B，（2）Cn（X）∩C=Ø，（3）如果X⊂Y⊆B，那么Cn（Y）∩C≠Ø。

这里把B▽C称为C-保留集，把B▽C的元素称为C-保留（C-remainder）。由条件（1）和（2）知，此“C-保留”的直观意思是指在逻辑上去除C中所有内容后保留的部分；而且由条件（3）知，这样的C-保留都是B中极大的。当C中只有一个元素（如{φ}）时，将B▽C简记为B▽φ。如果C是{⊥}，那么C-保留就是B的极大一致子集。

保留集概念具有下面两个有趣性质，即上界性和等价性，这两个性质在后续定理证明中非常有用。

引理1（上界性[2]38）令B，C⊆L。如果Z⊆B且Cn（Z）∩C=Ø，那么存在X使得Z⊆X∈B▽C。

引理2（等价性）令M，N⊆L。那么M▽⊥=N▽⊥⇔∀φ∈（M∪N）（M∩N）（φ├⊥）。

证明：左边⇒右边：令左边成立。用反证法，假设∃φ∈（M∪N）（M∩N）使得φ⊥。分两种情况导出矛盾。φ∈MN的情况：由{φ}⊆M、{φ}⊥和上界性知存在X使得{φ}⊆X∈M▽⊥，故由左边得{φ}⊆X∈N▽⊥，故φ∈N，产生矛盾；φ∈NM的情况：由对称性知可类似地导出矛盾，略。由于在这两种情况下都导出矛盾，故假设错误，因此右边成立。

右边⇒左边：令右边成立，分两个方向证明左边。M▽⊥⊆N▽⊥：令X∈M▽⊥。故X⊆M且X⊥。假设XM∩N，故XN，故存在τ∈XN，故τ∈（M∪N）（M∩N），由右边得τ├⊥，故由τ∈X得X├⊥。这与X∈M▽⊥相矛盾，故假设XM∩N错误，X⊆M∩N⊆N成立。下证X∈N▽⊥。用反证法，假设XN▽⊥。由X⊆N、X⊥和定义2知存在Y⊆N使得X⊆Y且Y⊥。类似地，假设YM∩N，故由Y⊆N得YM，故存在τ∈YM，故τ∈（M∪N）（M∩N），由右边得τ├⊥，故由τ∈Y得Y├⊥，产生矛盾，故假设YM∩N错误，Y⊆M∩N⊆M成立。由X⊂Y⊆M和Y⊥得X∉M▽⊥，产生矛盾，故假设XN▽⊥错误，X∈N▽⊥成立，故M▽⊥⊆N▽⊥。M▽⊥⊇N▽⊥：由对称性知可类似地证明。证毕。

部分交代谢修正分为膨胀和巩固两个模块（或阶段）。由于膨胀模块只是信念库和新信息的集合并运算，故巩固模块才是部分交代谢修正的关键过程。这里巩固模块的主要功能是：在遭遇信念冲突时，借助核心信念和候选理论来发现和去除不可信信息，从而化解信念冲突或理论危机，并同时保护核心信念。那么如何发现并去除不可信信息呢？这里可仿照一票否决制的投票规则。在以投票作为决策方法的会议上，往往会有若干待议方案，而这些方案中往往会存在一些相互冲突的方案，需要作出取舍。如果一个方案遭到一个及以上投票者的慎重反对的话，那么这个方案很可能是有瑕疵或弊端的。如果参与这个决策会议的投票者都具有一票否决权的话，那么只要有一个投票者反对某方案，该方案就不会被采纳。只有那些被所有投票者都赞成或支持的方案才会被采纳。部分交代谢修正的巩固阶段也与此类似。就如第一节对例1的分析阐述所言，当出现信念冲突时，认知主体对这些冲突信念的不同取舍会导致不同的竞争性候选理论。这些候选理论既会“支持”一些信念，也会“反对”另一些信念。它们就相当于上述“投票者”，而每个信念就相当于一个“待议方案”。被候选理论所反对的信念很可能是不可信的信息。如果采用“一票否决制”的谨慎态度，那么这些不可信信息在巩固过程中都应当被放弃。只有那些被所有候选理论都支持的信念，才被保留下来。

当然，候选理论并不是随便形成的；不是越多越好，也并不是越少越好。虽然它们的形成依赖于认知主体的主观选择，但其候选资格却依赖于一些相对客观的理性条件。首先，由极大效用原则和一致性原则知，应尽可能地保留更多相互一致的有用信息；而且旧信念库B∪D里的可信信息都藏在它的极大一致子集里面；故可合理假定这些候选理论是B∪D的⊥-保留。其次，由保护性原则知，核心信念都应当在修正过程中保留下来，这要求候选理论都应当包含这些核心信念，即Cn（A）∩（B∪D）；否则，该理论不具有作为候选理论的资格。但是满足这两个理性条件的候选理论可能不止一个，因此认知主体需要进一步在众多候选理论中进行挑选。把挑选出来的若干合格的候选理论作为“投票者”，并把它们都支持的信念保留下来，而把那些受到一个及以上候选理论所反对的信念放弃掉。这就是部分交代谢修正的直观思想。更简洁地说，认知主体先从⊥-保留集中挑选出若干具备资格的⊥-保留作为候选理论，然后把它们的交运算结果作为新信念库，而把其他信念作为不可信信息放弃掉。

如图，R1和R2是认知主体所挑选的两个候选理论，它们都满足上述两个理性条件，是包含核心信念Cn（A）∩（B∪D）的⊥-保留。图中有四个区域：R1∩R2、（B∪D）（R1∪R2）、R1（R1∩R2）和R2（R1∩R2）。直观而言，R1∩R2里的信息比其他区域更加可信，因为它们都受到所有候选理论（即R1和R2）的支持（如果X├φ，那么称X支持φ），如核心信念Cn（A）∩（B∪D）。类似的，（B∪D）（R1∪R2）里的信息与其他区域的信息相比更加不可信，因为它们都受到所有候选理论的排斥①如果X├┓φ，那么称X排斥或反对φ。由于R1和R2都是⊥-保留，即B∪D的极大一致子集，所以根据定义2知它们各自与任何其他信念的并集都会导致矛盾。也就是说，候选理论R1和R2各自都排斥其他信念。，如Z1。居于这两个区域中间的是R1（R1∩R2）和R2（R1∩R2），它们内部的信息虽然都各自受到了一个候选理论的支持，但同时也受到了另一候选理论的排斥，从而也是不太可信的，如Z2。因此，可以理性地假定认知主体将候选理论R1和R2都支持的R1∩R2作为部分交代谢修正后保留的可信信息。正如例1中费教授的做法。

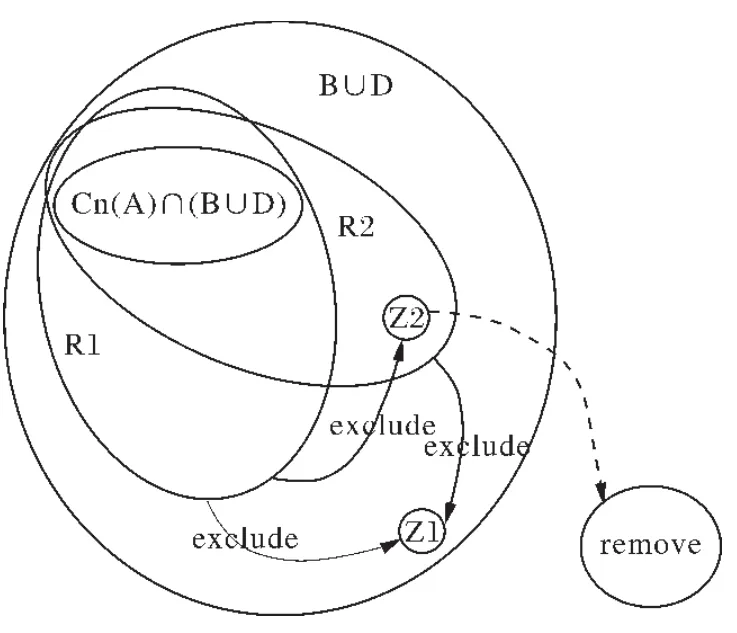
（图1）

下面来定义这种挑选候选理论的代谢选择函数。

定义3令（B，A）∈B。γ:P（P（L））→P（L）是基于（B，A）的代谢选择函数当且仅当对所有的保留集（B∪D）▽⊥，

（1）γ（（B∪D）▽⊥）⊆（B∪D）▽⊥，

（2）γ（（B∪D）▽⊥）≠Ø，且对每个X∈γ（（B∪D）▽⊥）都有Cn（A）∩（B∪D）⊆X。

这里有两点值得注意。第一，条件（2）的可行性取决于（B∪D）▽⊥中是否存在满足“Cn（A）∩（B∪D）⊆X”的⊥-保留，使得代谢选择函数可以将它们挑选出来。下面这个命题说明答案是肯定的。

命题2令（B，A）∈B且D⊆L。那么存在X∈（B∪D）▽⊥使得Cn（A）∩（B∪D）⊆X成立。

证明：由（B，A）∈B知Cn（A）∩{⊥}=Ø。由于Cn（A）∩（B∪D）⊆Cn（A），故Cn（Cn（A）∩（B∪D））∩{⊥}⊆Cn（A）∩{⊥}，从而Cn（Cn（A）∩（B∪D））∩{⊥}=Ø。由Cn（A）∩（B∪D）⊆B∪D、Cn（Cn（A）∩（B∪D））∩{⊥}=Ø和上界性知存在X使得Cn（A）∩（B∪D）⊆X∈（B∪D）▽⊥。证毕。

第二，定义3要求γ是函数。也就是说，对所有D1，D2⊆L，它必须满足下面这个条件：

（#）如果（B∪D1）▽⊥=（B∪D2）▽⊥，那么γ（（B∪D1）▽⊥）=γ（（B∪D2）▽⊥）。

那么这个条件是否与条件（1）、（2）相一致呢？这个问题是关键的，它关涉到γ是否是可构造的。下面命题表明答案是肯定的。

命题3令（B，A）∈B，并且∀D⊆L（γ（（B∪D）▽⊥）={X∈（B∪D）▽⊥|Cn（A）∩（B∪D）⊆X}）。那么γ满足定义3的条件（1）、（2）和条件（#）。

证明：条件（1）显然成立。条件（2）：由命题2易证。条件（#）：令（B∪D1）▽⊥=（B∪D2）▽⊥。由等价性得∀φ∈（（B∪D1）∪（B∪D2））（（B∪D1）∩（B∪D2））都有φ├⊥。假设Cn（A）∩（B∪D1）≠Cn（A）∩（B∪D2）。故存在ψ∈Cn（A）∩（B∪D1）使得ψ∉B∪D2或者存在ψ∈Cn（A）∩（B∪D2）使得ψ∉B∪D1。当前者成立时，ψ∈（B∪D1）（B∪D2），故ψ├⊥，再由ψ∈Cn（A）得A├⊥，这与（B，A）∈B相矛盾；当后者成立时，可类似地导出矛盾。因此假设错误。从而由γ的定义和（B∪D1）▽⊥=（B∪D2）▽⊥可得γ（（B∪D1）▽⊥）={X∈（B∪D1）▽⊥|Cn（A）∩（B∪D1）⊆X}={X∈（B∪D2）▽⊥|Cn（A）∩（B∪D2）⊆X}=γ（（B∪D2）▽⊥）。即γ（（B∪D1）▽⊥）=γ（（B∪D2）▽⊥）。故条件（#）成立。证毕。

有了代谢选择函数，下面来定义部分交代谢修正算子的函数式构造，将候选理论皆赞成或支持的可信信息保留下来。

定义4令（B，A）∈B，γ是基于（B，A）的代谢选择函数。

（1）由γ构造的基于（B，A）的部分交代谢修正算子◇γ是这样定义的：对所有的D⊆L，（B，A）◇γD（B′，A′），其中B′=∩γ（（B∪D）▽⊥），A′=Cn（A）∩B′。

（2）算子◇是基于（B，A）的部分交代谢修正算子当且仅当存在代谢选择函数γ使得对所有的D⊆L，都有（B，A）◇D（B，A）◇γD。

例子2令φ和ψ为不相关的原子命题，信念库B={φ，ψ}，核心信念集A={φ}，新信息D={┓φ，φ→ψ，┓φ→┓ψ，ψ}。据定义2易得（B∪D）▽⊥={{φ，φ→ψ，┓φ→┓ψ，ψ}，{┓φ，φ→ψ，┓φ→┓ψ}，{┓φ，φ→ψ，ψ}}。容易验证，满足定义3条件（1）（2）的选择方案只有一个，即γ（（B∪D）▽⊥）={{φ，φ→ψ，┓φ→┓ψ，ψ}}。由于B中的φ和D中的┓φ→┓ψ都是核心信念集A的逻辑后承，故受到γ的保护。由γ构造的部分交代谢修正算子对新信息D的修正结果为（B，A）◇γD（B′，A′），其中B′=∩γ（（B∪D）▽⊥）={φ，φ→ψ，┓φ→┓ψ，ψ}，A′=Cn（A）∩B′={φ，┓φ→┓ψ}。

三、表达定理

上面第一节和第二节分别对部分交代谢修正算子进行了公理性刻画和函数式构造。它们分别从公理性质和可计算函数这两个方面对部分交代谢修正过程进行了刻画。那么这两种刻画之间是什么关系呢？这种函数式构造是否等价于若干公理性假定的组合呢？这一节将证明它们之间具有等价性，即表达定理。表达定理是信念修正理论中最重要的结果，它是信念修正理论领域中的“完全性定理”。

定理1令（B，A）∈B。算子◇是基于（B，A）的部分交代谢修正算子当且仅当它满足：M-BelState，M-CoreInvariance，M-Inclusion，M-Consistency，M-Irrelevance和M-Relevance。

证明：（I）函数式构造⇒公理性假定：

M-BelState和M-Inclusion：容易证明，略。

M-CoreInvariance：由定义4知A◇BD=A′=Cn（A）∩B′，故只要证明Cn（A）∩B′=Cn（A）∩（B∪D）即可。⊆方向是显然的。假设Cn（A）∩B′Cn（A）∩（B∪D），故存在τ∈Cn（A）∩（B∪D）使得τ∉B′=∩γ（（B∪D）▽⊥）。由定义3得γ（（B∪D）▽⊥）≠Ø，再由τ∉∩γ（（B∪D）▽⊥）知存在X∈γ（（B∪D）▽⊥）使得τ∉X。再由定义3得τ∉Cn（A）∩（B∪D），产生矛盾，故假设错误。

M-Consistency：假设B◇AD├⊥，即∩γ（（B∪D）▽⊥）├⊥。由定义3得γ（（B∪D）▽⊥）≠Ø，从而每个X∈γ（（B∪D）▽⊥），都有X├⊥成立，与X∈（B∪D）▽⊥矛盾，故假设错误。

M-Irrelevance：令∀φ∈（（B∪D1）∪（B∪D2））（（B∪D1）∩（B∪D2））都有φ├⊥。由等价性得（B∪D1）▽⊥=（B∪D2）▽⊥。由γ的定义得γ（（B∪D1）▽⊥）=γ（（B∪D2）▽⊥）。故B◇AD1=∩γ（（B∪D1）▽⊥）=∩γ（（B∪D2）▽⊥）=B◇AD2，即B◇AD1=B◇AD2。故M-Irrelevance成立。

M-Relevance：令ψ∈（B∪D）B◇AD。故ψ∈B∪D且ψ∉B◇AD=∩γ（（B∪D）▽⊥）。又由定义3（2）得γ（（B∪D）▽⊥）≠Ø，故存在X∈γ（（B∪D）▽⊥）使得ψ∉X，并由ψ∈B∪D和定义3（2）知ψ∉Cn（A），即Aψ。令C=X，由X∈γ（（B∪D）▽⊥）得∩γ（（B∪D）▽⊥）⊆X，即B◇AD⊆C。由C∈（B∪D）▽⊥得C是一致的，并且由ψ∉X=C和ψ∈B∪D得C⊂C∪{ψ}⊆B∪D，故由定义2和C∈（B∪D）▽⊥得C∪{ψ}是不一致的。因此M-Relevance成立。

（II）公理性假定⇒函数式构造：

定义基于（B，A）的映射γ使其满足：对任意的D⊆L都有γ（（B∪D）▽⊥）={X∈（B∪D）▽⊥|B◇AD⊆X}。定义基于（B，A）的算子°使其满足：对任意的D⊆L都有（B，A）°D（B′，A′），其中B′=∩γ（（B∪D）▽⊥），A′=Cn（A）∩B′。下面要证明（a）、（b）和（c）。

（a）γ是良定义的函数：令（B∪D1）▽⊥=（B∪D2）▽⊥，这里要证γ（（B∪D1）▽⊥）=γ（（B∪D2）▽⊥）。由等价性和（B∪D1）▽⊥=（B∪D2）▽⊥可得∀φ∈（（B∪D1）∪（B∪D2））（（B∪D1）∩（B∪D2））都有φ├⊥。再由M-Irrelevance得B◇AD1=B◇AD2。因此，γ（（B∪D1）▽⊥）={X∈（B∪D1）▽⊥|B◇AD1⊆X}= {X∈（B∪D1）▽⊥|B◇AD2⊆X}={X∈（B∪D2）▽⊥|B◇AD2⊆X}=γ（（B∪D2）▽⊥）。

（b）γ是基于（B，A）的代谢选择函数：条件（1）：显然满足。条件（2）：由M-Consistency得B◇AD⊥，由M-Inclusion得B◇AD⊆B∪D，再由上界性知存在Y使得B◇AD⊆Y∈（B∪D）▽⊥。故由γ（（B∪D）▽⊥）的定义知Y∈γ（（B∪D）▽⊥）≠Ø。假设存在X∈γ（（B∪D）▽⊥）使得Cn（A）∩（B∪D）X成立。故存在τ∈Cn（A）∩（B∪D）使得τ∉X。再由X∈γ（（B∪D）▽⊥）={X∈（B∪D）▽⊥|B◇AD⊆X}得τ∉B◇AD。由τ∈B∪D、τ∉B◇AD和M-Relevance得Aτ，产生矛盾，故假设错误。因此条件（2）成立。

B◇AD=B′：由γ（（B∪D）▽⊥）的定义知每个X∈γ（（B∪D）▽⊥）都有B◇AD⊆X，又由（b）知γ（（B∪D）▽⊥）≠Ø，故B◇AD⊆∩（（B∪D）▽⊥）=B′。假设B′B◇AD，那么存在φ∈B′但φ∉B◇AD。由φ∈B′得φ∈∩γ（（B∪D）▽⊥），故∀X（（X∈γ（（B∪D）▽⊥））⇒（φ∈X））。由φ∈∩γ（（B∪D）▽⊥）得φ∈B∪D。由φ∉B◇AD、φ∈B∪D和M-Relevance知：存在C⊆B∪D使得B◇AD⊆C且C⊥但C∪{φ}├⊥。由C⊆B∪D、C⊥和上界性知存在Y⊇C使得Y∈（B∪D）▽⊥。由B◇AD⊆C和Y⊇C得B◇AD⊆Y，加上Y∈（B∪D）▽⊥可知Y∈γ（（B∪D）▽⊥）。在此前提下，再假设φ∈Y，再由Y⊇C可得C∪{φ}⊆Y，由于C∪{φ}├⊥，故Y├⊥，与Y∈（B∪D）▽⊥矛盾，故假设φ∈Y错误，φ∉Y成立。而由φ∉Y和Y∈γ（（B∪D）▽⊥）可得∃X（（X∈γ（（B∪D）▽⊥））∧（φ∉X）），这与上面的∀X（（X∈γ（（B∪D）▽⊥））⇒（φ∈X））相矛盾，故假设B′B◇AD错误，B′⊆B◇AD成立。因此，B◇AD=B′。

A◇BD=A′：由M-CoreInvariance和°的定义知即证Cn（A）∩（B∪D）=Cn（A）∩B′。⊇方向是显然的。假设Cn（A）∩（B∪D）Cn（A）∩B′，故存在τ∈Cn（A）∩（B∪D）使得τ∉B′=∩γ（（B∪D）▽⊥）。再由（b）中已证的γ（（B∪D）▽⊥）≠Ø可知存在X∈γ（（B∪D）▽⊥）使得τ∉X，再由X∈γ（（B∪D）▽⊥）可得τ∉B◇AD。由τ∈（B∪D）B◇AD和M-Relevance得Aτ，与τ∈Cn（A）相矛盾，故假设错误。

B°AD∈B：由B◇AD=B′、A◇BD=A′和M-BelState即得。证毕。

由命题1和定理1易得下面推论。

推论1令（B，A）∈B。如果算子◇是基于（B，A）的部分交代谢修正算子，那么它也满足：M-Vacuity，M-Protection和M-RelClosure。

四、结语

部分交代谢修正是一种先膨胀后巩固并同时保护理论硬核的信念修正过程。本文采用AGM研究范式对它进行了公理性刻画，并通过“候选理论”和“核心信念”这两个概念来分析阐述认知主体对不可信信息的发现与清除，进而给出了基于保留集的函数式构造，最后证明了公理性假定和函数式构造这两种形式刻画方式之间的等价性，表明了部分交代谢修正算子具有形式上的“完全性”。这种分析刻画从符号逻辑的角度阐述了理论危机的产生和化解过程的各种细节，能够促进对现实生活中的信念冲突与修正现象的更加精致的高阶认知。此外，人工智能研究者也可以从这种形式认识论的思想中得到借鉴，设计出更加符合现实的、更具个性的、更有原则立场的认知主体。

[1]Alchourrón，C.，Gärdenfors，P.，Makinson，D.On the logic of theory change：Partial meet contraction and revision functions[J].Journal of Symbolic Logic，1985，50（2）.

[2]Hansson，S.O.A textbook of belief dynamics：Theory change and database updating[M].Dordrecht：Kluwer Academic Publishers，1999.

[3]Fermé，E.，Hansson，S.O.AGM 25 years：Twenty-five years of research in belief change[J].Journal of Philosophical Logic，2011，（40）.

[4]Yuan，Yongfeng，Ju，Shier.Rational evaluation in belief revision[J].Synthese，2015，192（7）.

[5]Yuan，Yongfeng，Ju，Shier，Wen，Xuefeng.Evaluative multiple revision based on core beliefs[J].Journal of Logic and Computation，2015，25（3）.

[6]Hansson，S.O.A survey of non-prioritized belief revision[J].Erkenntnis，1999，（50）.

[7]袁永锋.核心代谢修正算子[J].湖南科技大学学报：社会科学版，2015，（6）.

[8]舒卓，朱菁.证据与信念的伦理学[J].哲学研究，2014，（4）.

[9]Lakatos，I.Falsification and the methodology of scientific research programmes[M]//I.Lakatos，A.Musgrave.Criticism and the Growth of Knowledge. Cambridge：Cambridge University Press，1970.

[10]Makinson，D.Screened revision[J].Theoria，1997，（63）.

[11]Alchourrón，C.，Makinson，D.Hierarchies of regulations and their logic[M]//R.Hilpinen.New studies in deontic logic：Norms，actions，and the foundations of ethics.Dordrecht：D.Reidel Publishing Company，1981.

［责任编辑：熊显长］

B81

A

1001－4799（2016）06－0025－07

2016-05-16

国家社会科学基金青年资助项目：16CZX051；中国博士后科学基金资助项目：2015M581778

袁永锋（1986-），男，广东兴宁人，南京大学哲学系助理研究员，哲学博士，主要从事哲学逻辑研究。