Development of Composite Cellular Cores for Sandwich Panels Based on Folded Polar Quadra-Structures

Valentin Khaliulin,Wang Zhijin,Gershtein E M

1.Kazan National Research Technical University Named After A.N.Tupolev,Kazan 420111,Russia;

2.Minister Key Discipline Laboratory of Advanced Design Technology of Aircraft,

Nanjing University of Aeronautics and Astronautics,Nanjing 210016,P.R.China

Development of Composite Cellular Cores for Sandwich Panels Based on Folded Polar Quadra-Structures

Valentin Khaliulin1,Wang Zhijin2*,Gershtein E M1

1.Kazan National Research Technical University Named After A.N.Tupolev,Kazan 420111,Russia;

2.Minister Key Discipline Laboratory of Advanced Design Technology of Aircraft,

Nanjing University of Aeronautics and Astronautics,Nanjing 210016,P.R.China

An idea to develop a family of cellular cores for sandwich panels using a technology of prepreg folding is presented.Polar folded quadra-structures are regarded as a geometric basis for these cores whose standard fragment has the fourth degree of axial symmetry.The classification of the polar structures are described and a method of various quadra-structure synthesis is developed.A possibility to provide high strength of the structure due to preservation of faces reinforcement pattern is presented.Arrangement of the plane core on a bi-curvature surface is also introduced.Besides,provision of isotropy of the core in two or three directions are described.Einally,examples of cellular folded cores manufactured from basalt reinforced plastic are demonstrated.

composite sandwich panel;cellular core;folded polar quadra-structure;synthesis of cellular structure; quadra-structure classification

0 Introduction

This paper proposed a subclass classification of folded cores for sandwich panels with cellular structure.Cellular structure is a structure formed by periodically repeated cup-shaped elements. Unlike honeycomb structures composed of tubular elements(honeycombs),standard units of cellular structures create cavities that are separated from each other and distribute on one side of the skins[1](Fig.1).Despite being inferior to honeycombs in strength,cellular structures have a range of advantages.Eor example,they may be arranged on bi-curvature surfaces from the initial two-dimensional state.Cells may be interconnected,providing the possibility to remove moisture from the panel.Cellular cores have a large skin bonding area.There is a possibility to develop efficient energy absorbing panels based on cellular structures.

Fig.1 Cellular core

Limited application of cellular cores is associated with high-strength material processing problems.Only plastic materials with increased ultimate extensional strain are applicable for cupshaped cells molding.These materials usually have rather low specific mechanical properties.

Currently,cellular cores are produced from a range of materials,including thermoplastic ones using vacuum molding or automatic injection machines and casting mold(Fig.1(a)).These cores have low strength and cannot be used in aerospaceor naval structures.

*Corresponding author,E-mail address:zhijin@nuaa.edu.cn.

How to cite this article:Valentin Khaliulin,Wang Zhijin,Gershtein E M.Development of composite cellular cores for sandwich panels based on folded polar quadra-structures[J].Trans.Nanjing Univ.Aero.Astro.,2016,33(5):519-528. http://dx.doi.org/10.16356/j.1005-1120.2016.05.519

At the same time,there is a case of so-called″hypar″cellular structure(Fig.1(b))application in the nosing of An-124 aircraft.It is produced from glass-fiber prepreg using complex technology.Due to the fact that glass fiber does not allow large elongation values and it has a limited drapability,the process has low quality stability.Besides,it is impossible to produce a core with deep relief.

In recent years,braided cellular cores started to appear(Fig.1(c)).The main disadvantages of such structures are thin fiber placement as well as large fiber bending,which decrease the strength of the structure.

Therefore,creating a technology that will allow implementation of the ultimate properties of composites in cellular cores is essential.

Considering the fact that drawing with large elongation is not allowed for composites,a processing scheme based on a blank(a prepreg of dry fabric)folding into a cellular core seems to be an efficient way.

Eolded structure is a faceted surface that can be unfolded into a plane sheet and consists of repeating uniform fragments,composed of polygonal faces[2].

Eolded structures are formed from a sheet by means of isometric transformation,i.e.faces are not deformed.Herein this property provides permanence of faces reinforcement pattern in the process of cellular structure manufacturing.As a result,ultimate composite properties are guaranteed in the faces of the folded core.

1 Types of Folded Structures

Each folded structure has its own standard repeated fragment[3],a so-called elementary unit (EU).EU defines all geometric properties of the structure as well as the kinematics of its transformation[1-2].

An EU has a minimum required amount of faces,which is enough for identification of the structure[2].One of the main EU characteristics is its degree of symmetry[2,4].

There are two large subclasses of folded structures based on the type of symmetry and the alignment of EUs[5],which are row structures and polar one(Fig.2).

Fig.2 Examples of elementary units in folded structures

Degrees of symmetry of the row folded structures are less than three,i.e.they have only one mirror symmetry.Their geometric properties are different in two orthogonal directions.As a result,EU of these structures is located in rows (Figs.2(a,b)),thus giving their name[6-8].

EU of polar structures has a geometric center—A pole,and geometry of the structure is formed around it(Figs.2(c—e)).EU has a degree of symmetry corresponding to this or that structure.The degree of symmetry is defined by a factor k.

whereαis the minimum angle of EU rotation around the pole that is required for its complete alignment with a stationary one.

Polar structures have identical geometric properties in two or three directions and it is convenient to examine them in orthogonal and hexagonal grids,respectively(Figs.2(c—e)).Their EUs are always located in the nodes of two-and three-axes grids at regular intervals from each other.

As for the configuration of the structures, the row ones may be characterized as crimped and polar ones as cellular.The polar structures are discussed in the paper as a geometric basis for sandwich panel′s cellular cores[9].

2 Polar Structures with Various Degrees of Axial Symmetry

Currently we can talk about three groups of polar structures with third,fourth and sixth degree of axial symmetry,and we will call them trio-(T),quadra-(K)and hexa-(G)structures,respectively.

Figs.2(c—e)show random structures representing each group.Eor EU to be aligned with its initial position in a trio-structure,it should be rotated 120°.It is rotated around Pole A in the triangle.EUs in quadra-and hexa-structures (Figs.2(d,e))should be rotated 90°and 60°,respectively.

It should be noted that trio-and hexa-structures will have uniform properties in three directions relative to the pole,while quadra-structures will have uniform properties in two directions. Thus,polar structures will have a higher nominal isotropy compared with row structures.

3 Cellular Structures Synthesis

Various structural configurations are concerned when folded cellular structures are being developed.It appears that there is an infinite multitude of polar folded structures and the architectures are not logically related.This paper proposes a feasible approach to classify polar folded structures.

This method is based on the following principles:

Eirst,it has been a consensus that there are only three large groups of polar folded structures: trio-(T),quadra-(K)and hexa-(G).However, it has not been proved yet.

Then,each group has a primary structure, so called″maternal structures″.Maternal structures have a certain peculiarity:none of them can be obtained from another by the reduction of amount of structural elements.In other words,if we compare relative structures based on the amount and location of structural elements,the maternal one will be the simplest and will contain a minimal amount of faces and ribs.

A compensator is a fragment of a structure that is composed of a few connected faces.When they rotate around the ribs,the structure will be converted.Thus,compensators make the transformation of a plane surface into faceted possible.

By far,three types of compensators are known.Compensators applied on quadra-structures are shown in Fig.3.

Fig.3 Compensators of quadra-structures and their transformation

Z and V compensators obtain their names due to a similarity to the primary row four-axis structures[5]:Azimuthal—Z-crimp and reverse—V-crimp.S compensator is another type.It has not previously been used in row structures.

Peculiarity of maternal structures is entirely determined by the compensator they are composed of.

The amount of compensators and their location corresponds to the degree of axial symmetry of the structure.Eor example,Fig.4 demonstrates elementary units of three existing types of quadra-structures with Z,V and S compensators. In all three cases,the logic of compensators for placement is defined by the orthogonality of the grid.

Fig.4 Elementary units of quadra-structures

It should be noted that all three groups of structures—trio,quadra and hexa are built on the same Z,V and S compensators.Degree of symmetry and compensator define the abbreviation of the structure:TZ,TV,TS for trio-structures; KZ,KV,KS for quadra-structures and GZ,GV, GS for hexa-structures.

As an example,Fig.5 illustrates three possible maternal quadra-structures with Z,V and S compensators.

Fig.5 Maternal structures generated from compensators

Einally,a feasible method to develop new structures by maternal modification is studied.

Modification methods are borrowed from row structures technology[9].Basic methods of modification are as follows:

Global—drawing the ribs apart parallel to the initial position.As a result,a new rectangular face appears between the initial faces(Figs.6(a, b)).

Local—fan-type drawing of the ribs,when a rib on one side stays still.As a result,there are new triangular faces(Fig.6(c)).

Combined global and local—simultaneous drawing up and angular motion of template lines (Fig.6(d)).As a result,trapezoid faces appear.

Parametric—modification of the length and angle of the rib on the template.The total amount of faces and angles in each face does not vary.As a result,only initial shape of the faces is distorted.

Symbols,shown in Figs.6(a,b),illustrate global modification,such as drawing coordinate and diagonal lines up,respectively.Symbols of Fig.6(c)demonstrate local modification for the line that has an end on one side,so it is a fan-type drawing up.Symbols of Fig.6(d)show that the line is modified both locally and globally.

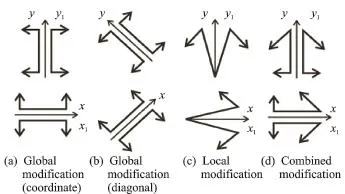
Fig.6 Symbols for modification methods

4 Examples

4.1 Z compensator based quadra-structures modification

KZ and KV maternal quadra-structures(Fig.5) have a flat relief and low concentration of structural elements.These peculiarities make themunattractive for application as sandwich panel cores.They may be applied in the structure of heat-exchanging lamellar devices or as a decorative facing. The structures developed by modification methods are more attractive. Fig.7 illustrates the results of KZ maternal structure modification.Elementary units are located on the orthogonal grid and have the fourth degree of symmetry as shown in the figure. Modification can be carried out in the following way. Maternal structure(Fig.7(a))is entirely composed of triangular faces.It is a set of pyramids,when compressed. After global modification along orthogonal lines of the template(Fig.7(b))rectangular tilted faces as well as square faces in the pole zones appear.Relief of the structure becomes deeper and the volume of the structure becomes more saturated with faces. Global modification along the diagonal lines (Fig.7(c))also leads to development of rectangular side faces and square faces.Square faces are rotated 90°toward coordinate lines. Unlike the previous example,relief corresponding to the plane state of faces in this structure is more sloping.The volume of the structure has a small concentration of faces. Local modification(Fig.7(d))provides squares in the pole zones.All faces are triangular. Fig.7(e)shows a structure,developed by combined modification—global and local. As a result,octagonal faces appear in the upper surface and square faces appear in the median surface.There are still triangular faces,while trapezoidal faces are still the majority. It should be noted that all developed KZ structures have a double mirror symmetry about coordinate and diagonal lines apart from the fourth degree of axial symmetry.

4.2 Synthesis of quadra-structures with V compensator Application of V compensator lies on the ba-sis of KV structures(Fig.3(b)).V compensator is borrowed from the technology of row reverse structures.It consists of two four-axis nodes that provide a transformation of the structure.

Fig.7 Modifications of KZ structure(templates and 3D models)

Similar to the case of KZ structure,peculiar geometry appears as a result of modification: Square areas appear in the upper and lower surfaces in the nodes of the grid,while side faces become tilted and obtain rectangular and trapezoid shape.Most of the structures have a sloping surface and low concentration of structural elements when folded.

Fig.8 demonstrates structures developed from the maternal one via modification.

Only two structures(Figs.8(b,e))have deep relief and may be useful for practical application.

Fig.8 Modification of KV structure(templates and 3D models)

4.3 Synthesis of quadra-structures with S compensator

Maternal structure based on S compensator is significantly different from KZ and KV structures in its involuntary properties.It does not get double mirror symmetry and that is why in this case it is not possible to apply global and local modification.

Size compensation during transformation is provided by the rotatory movement of a square face 1 around its center and folding of Eaces 2,3 (Fig.3(c)).

Fig.9 shows a process of maternal KS structure modification,which includes drawing the lines a-a′,b-b′,c-c′and d-d′of each compensator up on a double width of a square.As a result, rectangular faces with sides a-a1,b-b1,c-c1and dd1appear(Fig.9(b)).This procedure reminds of global modification of KZ and KV structures.

Fig.9 Modification of maternal KS structures

Fig.10 demonstrates the examples of cellular structures developed from maternal KS structure (Fig.10(a))by modification similar to the global method.

Fig.10 KS structures

4.4 Parametric modification of quadra-structures[10]

Quadra-structures as well as row structures can be parametrically modified.When the structure is parametrically modified,the contents of the structure do not change,i.e.the amount and type of faces as well as connection between the faces keep unchanged.Angles at the faces and proportions between ribs length are modified accordingly.These modifications,seems insignificant,may result in a considerable change of the structure architecture.

Parametric modification must be very efficient in case it is necessary in order to synthesize a structure with practically applicable geometry. A few examples of parametric modification and its capabilities are reviewed below.

Fig.11 demonstrates two KV structures developed by global modification.Obviously,it is reasonable to introduce significant changes into geometric properties of the structures,varying the size of triangle and square.

Fig.11 Modification of relief by variation of template parameters during global modification of KV structure

As for KZ structure,the same result can be observed by combined modification.

Fig.12(a)shows globally modified KZ structure.If Triangles 1,2 are uniform and proportions between the sizes of structural elements are modified,we get a structure,indicated in Fig.12 (b).This structure has a very dense relief with compact arrangement of cubical elements with vertical side faces.

A large variety of architectures may be developed via modification of KS structures.

Fig.13 illustrates possible variants of KS structure No.3 modifications.These modifica-tions are performed by transformation of a right triangle(Fig.13(a))into an distorted triangle (Fig.13(b))and an isosceles triangle (Figs.13(c,d)).

Fig.12 Modification of relief by varying template parameters

Fig.13 Possible schemes of parametric modification of KS structure No.3

As a result of such transformations,it is possible to change the mutual orientation of square faces 3 and 4 as well as their sides′size proportions.

Parametrically modified structure No.3 has amazing geometric properties.Fig.14 shows atemplate and the structure itself.

Fig.14 Parametrically modified KS structure No.3

It is obvious that the structure has solid upper and lower surfaces and consists of closed chambers that have a shape of pyramids or prisms.During transformation right-triangle faces are replaced with isosceles-triangle ones and square faces 1 and 2 are rotated 90°.

4.5 Comparison of properties of quadra-structures

The geometric properties of quadra-structures are reviewed from the point of possibility and aptness of their application as light cores for sandwich panels.

The majorities of KZ and KV structures,developed via modification,have a sloping relief and low concentration of structural elements.It makes them unattractive for such application as light cores for sandwich panels.They may be applied as heat exchange lamellar devices or decorative coating,with the exception of structures,locally modified along coordinate lines(Fig.7(d)—KZ structure and Fig.8(d)—KV structure). Their advantages are large depth of the cell and the possibility to increase the ratio between the height of the structure and the area of supporting square elements.This is how large concentration of vertical structural elements may be achieved. The disadvantages are as follows:Connection of faces creates a lock with penetration of a few faces into truncated tetrahedral pyramids.Such configuration makes it difficult to produce such core using existing methods[11].

There is an interesting KV structure,developed via combined modification along coordinate axes and diagonal lines(Fig.8(e)).Its configuration is close to″hypar″structure,which is applied in the aerospace industry(Fig.1(b)).Eunctionality of KZ and KV structures may be increased by variation of template parameters(Figs.11, 12).The same applies to the structures obtained via combined modification along coordinate axes.

Geometric properties of KS structure fit better for their practical application,for example,as light cores in sandwich panels.

Advantages of these structures are as follows:

(1)Close arrangement of cubic cells.

(2)Absence of tilted elements(faces).

(3)Close contact between the vertical faces.

(4)Regular alternation of square faces in upper and lower surfaces of the structure.

(5)Absence of lock-type contacts between the faces.

Aforementioned advantages define superior mechanical properties of the core,including strength of″core-skin″connection.

Disadvantages are a rigid connection between the sizes of vertical and horizontal ribs.These structures(unlike KZ and KV ones)cannot have a various height while the size of horizontal faces keep unchanged.Structural element concentration cannot be changed when the height of the structure is fixed.

Trio-(T)and hexa-(G)structures are not considered in this paper.Methods of modification for those structures have much in common with the method used for quadra-structures.

5 Practical Applications of Polar Structures

The most prospective area of polar structures application can be a geometric basis for the cores of sandwich panels.

Main advantages of the presented idea of cellular cores development are obviously a possibility to achieve the maximum mechanical capabilities of composite material due to the thing that reinforcement pattern is not distorted in the faces andthe faces stay plane[12].

Geometrical backgrounds for high performance of the structures are:

(1)Large concentration of vertical structural elements.

(2)Large area of the faces in enveloping surfaces.

(3)Uniform stiffness in two or three directions.

(4)Uniform transformability in a few direction,that allows arranging them on bi-curvature surfaces[13].

Figs.15,16 show quadra-and hexa-structure,that illustrate a possibility to develop sandwich bi-curvature shells.

Fig.15 Quadra-structure

Fig.16 Hexa-structure

Fig.17 shows specimens of the cores from basalt reinforced plastic with quadra-and hexastructure,that are manufactured using synchronous folding technology[14,15].

6 Conclusions

A technological idea of cellular cores manufactured using the folding method for sandwich panels is suggested.

Also,a method of classification of polar structures with various degrees of axial symmetry is developed.This classification is based on selecting the simplest structures as maternal ones.And all other structures are developed from maternal via a set of standard modification methods.

Fig.17 Examples of basalt reinforced plastic cores

Erom a practical point of view,polar structures are quite promising,because it is possible to forecast high mechanical properties.Besides, while being plane in initial state,they can be arranged on a bi-curvature surface.

Acknowledgement

This work was supported by the Ministry of Education and Science of Russian Eederation(No.REMEEI57414-X0078).

[1] KHALIULIN V I,SHAPAEV I I.Technology of composite parts manufacturing[M].Kazan:[s.n.], 2004.(in Russian)

[2] KHALIULIN V I.Technological schemes of sandwich panels manufacturing[M].Kazan:[s.n.], 1999.(in Russian)

[3] SEBASTIAN E.Aluminum foldcores for sandwich structure application:Mechanical properties and EE-simulation[J].Thin-Walled Structures,2015,90: 31-41.

[4] VEIL G.Symmetry[M].Moscow:[s.n.],1968. (in Russian)

[5] KHALIULIN V I.Classification of regular row-arranged folded structures[J].Russian Aeronautics, 2003,46(2):8-17.(in Russian)

[6] KHALIULIN V I,INKIN V A.Calculation of process variables at composite Z-crimp shaping using the folding method[J].Russian Aeronautics,2012, 55(4):417-423.

[7] DVOEGLAZOV I V,KHALIULIN V I.A study ofZ-crimp structural parameters impact on strength under transverse compression and longitudinal shear [J].Russian Aeronautics,2013,56(1):15-21.

[8] SHABALIN L P,SIDOROV I N,KHALIULIN V I.Simulation of Z-crimp shaping with the use of the ANSYS finite element software[J].Russian Aeronautics,2010,53(3):339-344.

[9] WANG Z,KHALIULIN V I,SKRIPKIN E.Geometry design method of folded structure[J].Journal of Nanjing University of Aeronautics and Astronautics, 2002,34(1):6-9.(in Chinese)

[10]KHALIULIN V I.A technique for synthesizing the structures of folded cores of sandwich panels[J]. Russian Aeronautics,2005,48(1):7-12

[11]KHALIULIN V I,DVOYEGLAZOV I V.On technological problems of fabrication of relief designs by isometric transformation of thin sheet[J].Transactions of Nanjing University of Aeronautics and Astronautics,2001,18(1):11-16.

[12]SHABALIN L P,GORELOV A V,SIDOROV I N, et al.Calculation of the parameters of stress-strain and ultimate states of composite foldcores under transverse compression and shear[J].Mechanics of Composite Materials,2012,48(4):415-426.

[13]RAZDAIBEDIN A A,KHALIULIN V I.Determination of processing parameters for the folded core with enveloping curvilinear surface[J].Russian Aeronautics,2015,58(1):88-95.

[14]KHALIULIN V I,BATRAKOV V V.Technological schemes of Zigzag crimp shaping[J].Russian Aeronautics,2005,48(2):106-114.

[15]KHALIULIN V I,RAZDAIBEDIN A A,MENYASHKIN D G.Evaluation of influence of processing parameter instability on the accuracy of folded cores[J].Russian Aeronautics,2005,48(3):94-101.

Prof.Valentin Khaliulin received Ph.D.and Doctor degrees in engineering from Kazan Aviation Institute,Kazan, Russia,in 1979 and 1997,respectively.Erom 1973 to present,he has been with the Aircraft Manufacturing Department,Kazan National Research Technical University n.a.A.N.Tupolev-KAI(KNRTU-KAI),where he is currently a full professor,the Head of Aircraft Manufacturing Department and the Head of the Center of Composite Technology.His research is focused on the technology of lightweight structures,such as folded cores for sandwich panels,and composite parts with high degree of integrity. Prof.Wang Zhijin received B.S.degree in airplane design from Nanjing Aviation Institute in 1983 and Ph.D.degree in design of flight vehicle from Moscow Aviation Institute. She joined in Nanjing University of Aeronautics and Astronautics in September 1983.Erom September 2007 to December 2007,she was a visiting scholar in the″MATI″-Russian State University of Aviation Technology named after K.E.Tsiolkovsky.Her research is focused on optimization of composite structure,design of light-weight structure and thermal structure design.

Ms.Gershtein E M graduated from Kazan State Technical University n.a.A.N.Tupolev,Kazan,Russia,in 2008. In October 2008,she joined in the Aircraft Manufacturing Department,Kazan National Research Technical University n.a.A.N.Tupolev-KAI,Kazan,Russia,as an engineer. In October 2013,she became a lead engineer and a postgraduate student at the Aircraft Manufacturing Department.Her research is focused on the technology of lightweight structures,such as folded cores for sandwich panels.

(Executive Editor:Xu Chengting)

V258 Document code:A Article ID:1005-1120(2016)05-0519-10

(Received 11 July 2016;revised 9 August 2016;accepted 9 September 2016)