基于U-D分解的卡尔曼滤波法在地下水污染源识别中的应用

崔尚进，卢文喜*，顾文龙，常振波，罗建男（1.吉林大学地下水与资源环境教育部重点实验室，吉林长春 130012；2.吉林大学环境与资源学院，吉林 长春 130012）

基于U-D分解的卡尔曼滤波法在地下水污染源识别中的应用

崔尚进1，2，卢文喜1，2*，顾文龙1，2，常振波1，2，罗建男1，2（1.吉林大学地下水与资源环境教育部重点实验室，吉林长春 130012；2.吉林大学环境与资源学院，吉林 长春 130012）

采用U-D分解的方法对常规卡尔曼滤波进行改进，以提高反演结果的有效性和可靠性.借助假想算例，引入模糊集合理论，将污染羽以模糊集的形式表示，利用U-D分解的卡尔曼滤波方法不断更新复合污染羽，通过复合污染羽和单个污染羽间模糊集的对比更新潜在污染源权重，进而达到真实污染源位置识别的目的.算例结果表明该方法与常规卡尔曼滤波方法相比具有更高的可靠性和有效性，能更好的达到污染源位置识别的目的.

污染源识别；U-D分解；卡尔曼滤波；模糊集

目前地下水污染治理已成为亟需解决的问题［1］.与地表水不同，地下水污染具有发现的滞后性和发生的隐蔽性，治理和修复过程复杂［2］.为了提出完善的治理方案，首先要对地下水污染源进行识别［3-4］.

现已有多种地下水污染源识别的方法，Atmadja等将这些方法分为四类：优化方法、解析方法、直接法、随机理论和地质学统计方法［5］.在这些方法中，优化法应用最广泛，如Aral等［6］通过逐次优化型遗传算法对污染源的位置和强度进行识别.随着研究不断深入，卡尔曼滤波方法被引入到污染源识别问题中.Zoi等［7］在污染源强度已知的情况下构建一个二维模型，采用卡尔曼滤波法以最少的采样成本对一个 DNAPL污染源达到识别目的.之后又利用卡尔曼滤波方法在污染源强度未知的三维模型中进行污染源识别的研究［8］.江思珉等［9］利用卡尔曼滤波方法结合单纯形法对地下水污染源进行识别.然而，常规卡尔曼滤波方法也存在数值不稳定易发散等弊端，因此引入U-D分解提高常规卡尔曼方法的数值稳定性［10］.

与常规卡尔曼滤波不同的是，U-D分解卡尔曼滤波从原理上解决了常规卡尔曼滤波方程中协方差矩阵可能出现不对称或负定的情况，反演结果更加可靠有效.通常在地下水污染源识别中，采样点的位置是固定的，这种情况下，常规卡尔曼滤波很可能出现不稳定和发散，以致无法达到污染源识别的目的，而U-D分解卡尔曼滤波却能很好的达到识别的目的.

1 U-D分解卡尔曼滤波原理

卡尔曼滤波由卡尔曼于1960年提出之后得到了广泛的应用如危岩预测、通信工程、地下水污染源识别等［11-14］.随着方法不断应用，其暴露的问题也越来越多，如数值稳定性较差，计算复杂性等［15-16］.

常规卡尔曼滤波的基本原理方程如下：

式中：K为卡尔曼增益矩阵；C为浓度；z为采样值；r为采样误差的方差；P为误差协方差矩阵；-和+分别表示先验信息和后验信息；H为1×n的矩阵，其中的元素只在采样点处为1，其他均为0，具体形式为H=［0..0，1，0…0］.

通过以上原理方程可以看出，式（3）中存在矩阵的相减运算，而在迭代过程中，当出现两个矩阵相减时，易导致数值稳定性不好，甚至会使滤波发散［17］.因此我们引入U-D分解对常规卡尔曼滤波进行改进，提高稳定性.

U-D分解卡尔曼滤波是将常规卡尔曼滤波方程中的误差协方差矩阵P分解为TPUDU= 形式，从而对整个方程重新推导.

其中

综上所述，网络语言的出现对汉语言文学的发展产生了一定的冲击。面对网络语言的冲击，人们应该加强对汉语言文学的学习，在日常生活和工作中重点对普通话和拼音进行推广和运用，并能够对网络语言进行合理控制，让汉语言文学经受住网络语言的冲击，并得到传承和发展。

以上方程式即为U-D分解卡尔曼滤波的原理，其中式（4）～（7）为主方程式.U为单位上三角矩阵，D为正定对角阵，两者代替了 P矩阵的迭代，保证了滤波的稳定性.

2 污染源位置识别方法

2.1 污染源位置识别算法流程

在固定采样点的地下水污染源位置识别中，采用以U-D分解卡尔曼滤波原理为基础，结合模糊集合理论，通过污染羽形态间的对比确定真实污染源的位置.U-D分解卡尔曼滤波方法的实现前提是要获得其原理方程中C-，D-，U-等先验信息.而流程图中前六步就是为了获取先验初始值，即首先获得污染源初始权重，假定渗透系数为随机变量生成随机场，进而获得浓度随机场，对其加权求和得到初始综合污染羽 C-和误差协方差矩阵P-，对P-进行U-D分解得到U-和D-.流程图中余下的步骤为该方法的具体实现，将采样值带入方程获得 C+，U+，D+等后验信息，从而得到更新后的污染羽，通过形态对比更新权重，循环该过程直到满足要求.

2.2 污染羽形态对比与权重更新

图1 污染源位置识别流程Fig.1 Contaminant plume location identification flow chart

在利用 U-D分解卡尔曼滤波进行污染源位置识别时，通过污染羽形态对比更新权重达到识别目的.污染羽采用模糊集的形式表示，若取n个标准αi则有n个不同标准的模糊集.将每个潜在污染源对应的模糊集污染羽与复合污染羽对比，以每个标准下的重叠面积为相似度，并加权求和为全局相似度，而标准化的全局相似度即为权重.

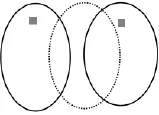
图2 污染羽形态对比Fig.2 Comparison of the contaminant plume shape

图2中虚线为复合污染羽，实线为单个潜在污染源的污染羽，通过对比右侧污染源与复合污染源在此标准下重叠面积大.将每一个标准下单个污染羽与复合污染羽对比，加权求和并标准化后得到权重.

3 假想算例分析

3.1 问题概述

图3 污染场地平面图Fig.3 Contaminated site plan

3.2 问题分析

在本问题算例中，渗透系数为随机变量，假设服从正态分布，均值为32m/d，标准差为1，首先利用拉丁超立方抽样结合相关性对该区域渗透系数场模拟实现了100次，将每次渗透系数场的实现与各个潜在污染源结合得到 300个污染质浓度场，取均值作为每个污染源对应的污染羽，加权求和得到初始复合污染羽.该问题中以真实污染源浓度场中的浓度值作为采样值，然后分别将采样值代入U-D分解的卡尔曼滤波方程中不断更新污染羽.

图4 综合污染羽和权重随采样点变化Fig.4 The change of composite contaminant plume and its source location weights with sampling point

选取污染羽形态变化过程中变化较为明显的时刻如图 4（a），（c），（e）所示，通过对比可以看出污染羽浓度中心逐渐向2号污染源靠拢，且污染羽整体形态与2号污染源单独排放形成的“单个污染羽”形态最为接近.从对应的权重图分析，2号污染源权重稳定为1，1号和3号污染源权重逐渐降低到标准以下.由此可以判断2号污染源为真实污染源.

考虑到采样值代入的顺序可能会对最终结果的影响，以不同的顺序分别将采样值代入U-D分解的卡尔曼滤波中，对比结果并无太大差异.由此证明采样点利用的顺序对最终结果影响甚微（由于篇幅原因，具体过程不再给出）.

图5 常规卡尔曼滤波结果Fig.5 Result of original Kalman filter

3.3 方法对比

利用常规卡尔曼滤波法解决该问题，得出的结果如图5所示.对比常规卡尔曼滤波和U-D分解的卡尔曼滤波所得到的结果（图 4（e））发现：在固定采样点时，常规卡尔曼滤波比较发散进而导致无法识别污染源，而U-D分解卡尔曼滤波更可靠有效，能很好的到达污染源识别的目的.

4 结语

4.1 在固定采样点时，U-D分解卡尔曼滤波能够很好的达到污染源位置识别的目的，反演结果可靠有效.

4.2 将采样点采样值代入到 U-D分解卡尔曼滤波中时，代入的顺序对最终结果没有影响.

4.3 在利用 U-D分解卡尔曼滤波识别污染源时，有可能出现采样点均已被利用但结果还未达到收敛要求的情况，因此如何再次增加采样点或者重复利用现有采样点，需要进一步展开研究.

［1］ 罗 兰.我国地下水污染现状与防治对策研究 ［J］. 中国地质大学学报（社会科学版）， 2008，8（2）：72-75.

［2］ 刘 博，肖长来，梁秀娟，等.吉林市城区浅层地下水污染源识别及空间分布 ［J］. 中国环境科学， 2015，35（2）：457-464.

［3］ 王红旗，秦 成，陈美阳.地下水水源地污染防治优先性研究 ［J］.中国环境科学， 2011，31（5）：876-880.

［4］ 肖传宁，卢文喜，安永凯，等.基于两种耦合方法的模拟-优化模型在地下水污染源识别中的对比 ［J］. 中国环境科学， 2015，35（8）：2393-2399.

［5］ Atmadja J， Bagtzoglou A C. State of the Art Report on Mathematical Methods for Groundwater Pollution Source Identification ［J］. Environmental Forensics， 2001，（2）：205-214.

［6］ Aral M M， Guan J， Maslia M L. Identification of contaminant source location and release history in aquifers ［J］. Journal ofHydrological Engineering， 2001，6（3）：225-234.

［7］ Zoi D， Pinder G F. Optimal search strategy for the definition of a DNAPL source ［J］. Journal of Hydrology， 2009，376（3/4）：542—556.

［8］ Zoi D， Pinder G F. Extension and field application of an integrated DNAPL source identification algorithm that utilizes stochastic modeling and a Kalman filter ［J］. Journal of Hydrology 2011， 398（3）：277-291.

［9］ 江思珉，张亚力，周念清，等.基于污染羽形态对比的地下水污染源识别研究 ［J］. 水利学报， 2014，45（6）：735-741.

［10］ 张友民，张洪才，戴冠中.一种U—D分解自适应推广卡尔曼滤波及应用 ［J］. 西北工业大学学报， 1993（3）：345-350.

［11］ 彭丁聪.卡尔曼滤波的基本原理及应用 ［J］. 软件导刊2009，11（11）： 32-34.

［12］ 伍仁杰，陈洪凯.卡尔曼滤波模型在危岩变形预测中的应用 ［J］.重庆工商大学学报：自然科学版， 2013，30（5）：1-4.

［13］ 江思珉，张亚力，周念清，等.基于卡尔曼滤波和模糊集的地下水污染羽识别 ［J］. 同济大学学报：自然科学版， 2014，3（3）：435-440.

［14］ 邱凤云. Kalman滤波理论及其在通信与信号处理中的应用［D］. 山东大学， 2008.

［15］ 张友民，戴冠中，张洪才.卡尔曼滤波计算方法研究进展 ［J］. 控制理论与应用， 1995，（5）：529-538.

［16］ 李 奕.自适应卡尔曼滤波在变形监测数据处理中的应用研究［D］. 长安大学， 2009.

［17］ 王满林.一种引入U-D矩阵分解的加速度模型卡尔曼滤波算法［J］. 舰船电子工程， 2008，2（2）.

全国人大常委会分组审议《环境保护税法（草案）》针对计税依据、征管程序、使用方向等提出修改意见和建议

9月2日，十二届全国人大常委会第二十二次会议分组审议了《环境保护税法（草案）》.参加审议的常委会组成人员和部分人大代表认为，本次提请审议的《环境保护税法（草案）》启动了以税治污的进程.《环境保护税法（草案）》提交人大审议，本身就标志着我们在加强法治建设上的一个进步，体现了税收法定的原则.制定这部法律有利于从根本上改变现行排污费制度存在的执法刚性不足、行政干预较多、强制性和规范性较为缺乏等问题，十分必要.《环境保护税法（草案）》给予“省、自治区、直辖市人民政府根据本地区污染物减排的特殊需要，可以增加同一排放口征收环境保护税的应税污染物种类数”的权力，同时强调了报同级人民代表大会常务委员会决定，并报全国人民代表大会常务委员会和国务院报备，体现了人大常委会在税收制定方面的权力.

在审议中，代表、委员们就环境保护税的法律名称、征税对象、计税依据、征管程序和税负平移等重要问题提出了进一步修改完善的意见和建议.

摘自《中国环境报》

2016-09-05

Application of U-D factorization-based Kalman filter to identify the groundwater pollution source.

CUI Shang-jin1，2，LU Wen-xi1，2*， GU Wen-long1，2， CHANG Zhen-bo1，2， LUO Jian-nan1，2（1.Key Laboratory of Groundwater Resources and Environment Ministry of Education， Jilin University， Changchun 130012， China；2.College of Environment and Resources，Jilin University， Changchun 130012， China）. China Environmental Science， 2016，36（9）：2633～2637

A improved Kalman filter， which was factorized by U-D method， was proposed to enhance the validity and reliability of the inverse strategy. The fuzzy set theory was introduced to represent contaminant plume in a hypothetical case. Then the weight of the potential source location was updated through the comparison of the composite plume updated by U-D factorization-based Kalman filter and the individual plume. The case study indicated that the U-D factorization-based Kalman filter has better reliability and validity， which can identify the location of pollution source better.

contaminant source identification；U-D factorization；Kalman filter；fuzzy set

X523

A

1000-6923（2016）09-2633-05

2016-01-16

国家自然基金项目（41372237，41502221）

* 责任作者， 教授， luwenxi@jlu.edu.cn

崔尚进（1993-），男，河南漯河人，吉林大学硕士研究生，主要从事地下水污染源反演识别方面的研究.