摩尔气体定压热容与定容热容之差之比的准确计算
2016-11-30吴义彬
吴义彬
(南昌市老科学技术工作者协会 江西 南昌 330003)
(收稿日期:2016-05-19)

摩尔气体定压热容与定容热容之差之比的准确计算
吴义彬
(南昌市老科学技术工作者协会 江西 南昌 330003)
(收稿日期:2016-05-19)
实际气体玻尔兹曼因子方程不仅与热力学基础知识一脉相承,涵盖并超越了理想气体方程、范德瓦尔斯方程与维里方程,而且在宏观特性参量与微观特性参量之间架起了衔接的桥梁,真正实现了对摩尔气体定压热容与定容热容之差、之比的准确计算.
玻尔兹曼因子方法 实际气体玻尔兹曼因子方程 摩尔表面自由能 定压热容 定容热容
1 引言
“热力学的优点是它的高度可靠性与普遍性,……,热力学不能给出关于物质特性的具体知识,这是它的缺点.”[1]“统计物理学正好弥补了热力学的这个缺点,解释了涨落现象.不但如此,统计物理学还可在对某种特殊物质作一些简单的物质的分子结构模型假设之后,推论出这种物质的特性.最重要的特殊物质的例子是理想气体.但统计物理学也有它的局限性.由于统计物理学中对物质的分子结构模型所作的简化假设只是实际的近似代表,所以理论的结果与实际不能完全符合.”[1]
由于玻尔兹曼因子方法既包含了分子之间的吸引力,也包含了相邻分子之间的排斥力,巧妙地迥避了“统计物理学处理互作用粒子系统所遇到的困难”[2],所以由玻尔兹曼因子方法推导出来的实际气体玻尔兹曼因子方程,不仅与热力学基础知识一脉相承,涵盖并超越了理想气体物态方程、范德瓦尔斯方程与维里方程[3],而且在物质的宏观特性参量(压强pq,摩尔体积Vqm,温度T)与物质的微观特性参量(摩尔表面自由能Fq)之间架起了衔接的桥梁,真正开启了精确计算物质微观特性参量Fq及其相关物质特性参量的大门,真正实现了对摩尔气体定压热容与定容热容之差、之比的准确计算.
2 摩尔气体定压热容与定容热容之差之比理论公式的推导
由均匀物质的热力学关系式,可以求得定压比热与定容比热的差[1]
(1)
“这是一个很重要的公式, 表明两个比热的差可以应用物态方程求出.”[1]
应用由玻尔兹曼因子方法推导出来的摩尔实际气体玻尔兹曼因子方程[4]
(2)
并在压强pq±Δpq,摩尔体积Vqm±ΔVqm,温度T±ΔT足够小的区间内,将摩尔表面自由能Fq视为常量,即可得到
(3)
(4)
将式(3)与式(4)代入式(1) 即可得到描述摩尔气体定压热容与定容热容之差的理论公式
(5)
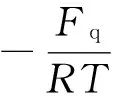
由于分子相互作用特性Fq可以通过宏观物理量pq,Vqm,T,由式(2)计算出准确的数值,所以,应用式(5)可以在理论上定量计算出摩尔气体定压热容与定容热容之差. 如果已知Cpqm,CVqm中的一个, 还可以在理论上定量计算定压热容与定容热容之比
(6)
或
(7)
3 摩尔理想气体定压热容与定容热容之差之比的准确计算
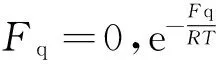
Cpqm-CVqm=R
(8)
(9)
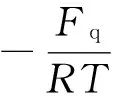
将25 ℃, 101.325 kPa压强条件下的氢气近似视为理想气体,且cpqm=14 268 J/kg·K[5], 氢气的分子量为2.015 7[5], R=8.312 8 J/mol·K,代入式(9) 即可得到
与氢气在0 ℃,101.325 kPa条件下的实验观测(查表)值1.407[5]吻合得很好.
4 摩尔实际气体定压热容与定容热容之差之比的理论计算
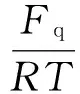
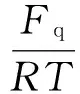
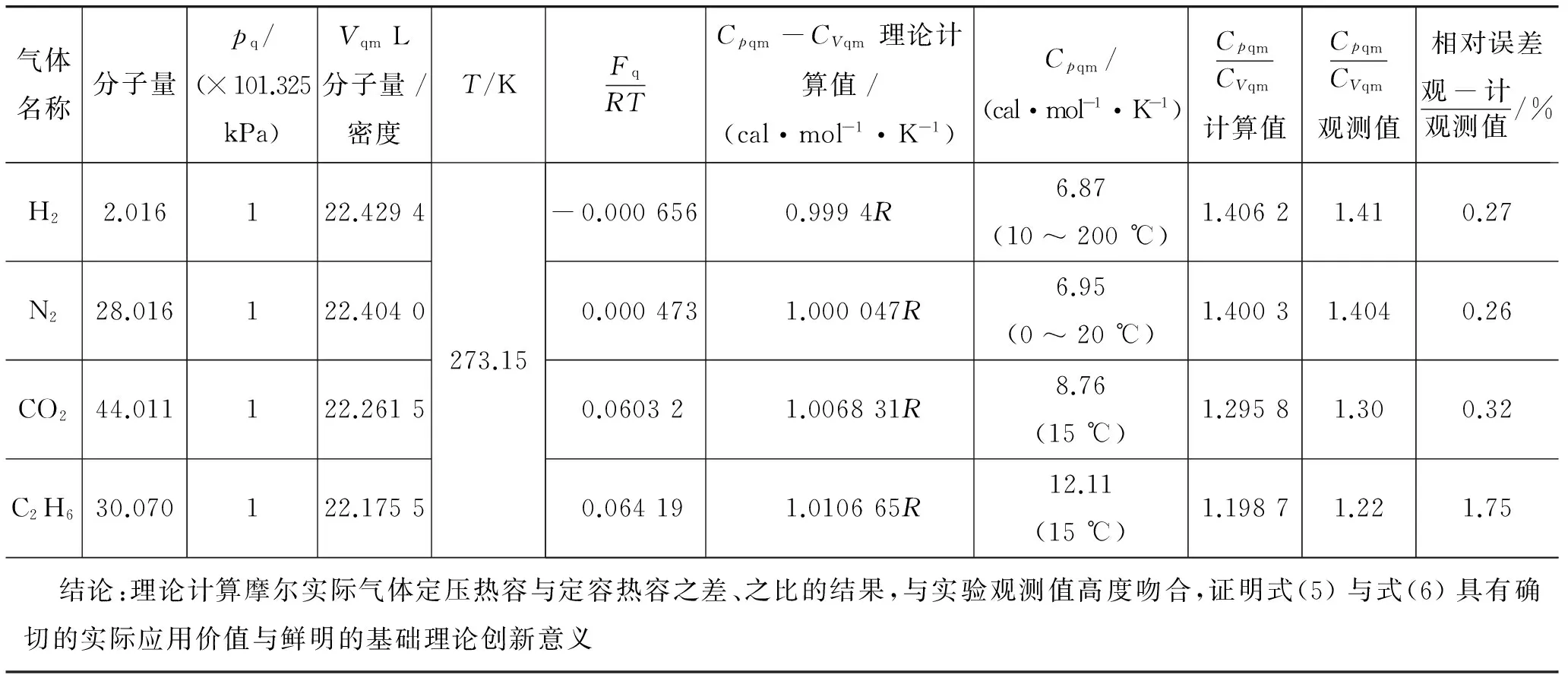
表1 摩尔实际气体定压热容与定容热容之差、之比的准确计算[6]
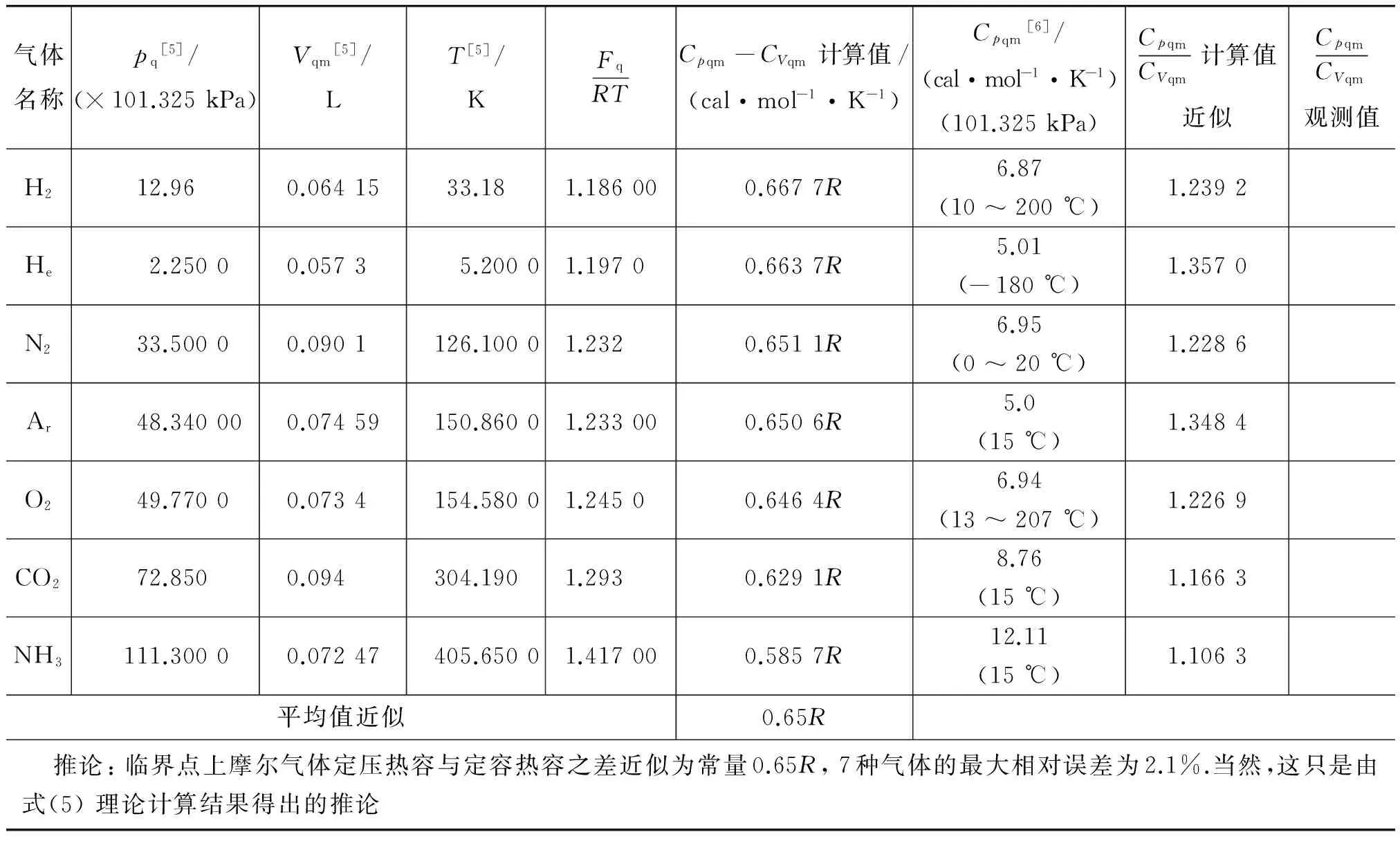
表2 临界点上摩尔气体定压热容与定容热容之差的准确计算与之比的近似计算
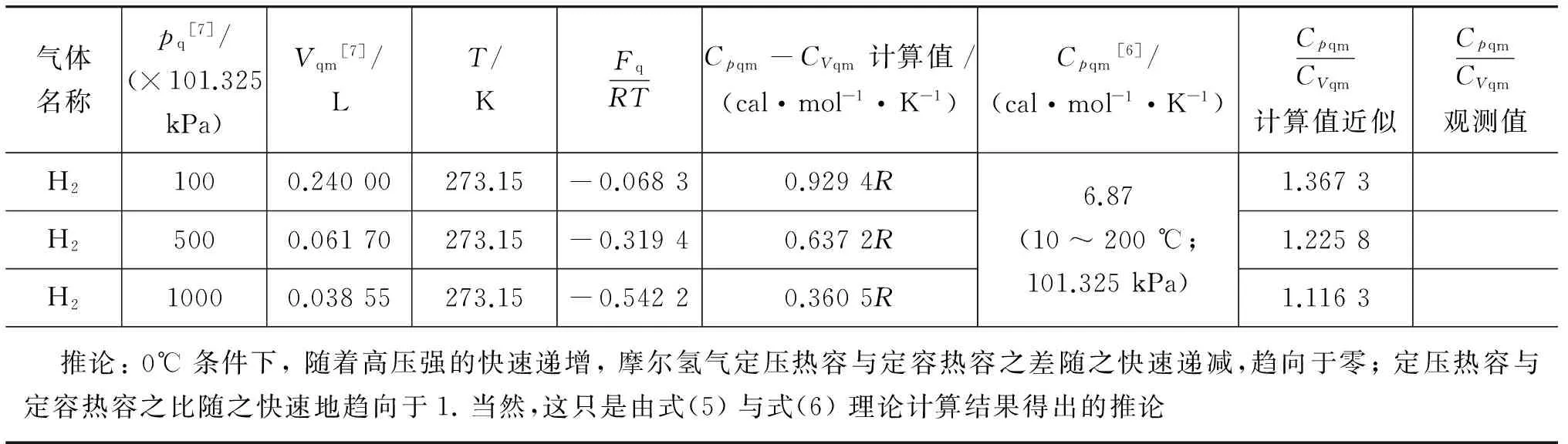
表3 0 ℃高压强条件下摩尔氢气定压热容与定容热容之差的准确计算与之比的近似计算
5 结束语
(1) 表1表明:对摩尔理想气体或实际气体定压热容与定容热容之差、之比进行理论计算的结果,与实验观测值高度吻合的事实证明:式(5)与式(6)正确有效,在“微观和宏观如何衔接的问题”上,具有确切的基础理论意义与实际应用价值.
(2) 表2和表3表明:由式(5)与式(6)导出的两个推论顺理成章,但却没有找到既有的实验事实可以证实或证伪.十分期待有兴趣者的关注、质疑、实验认证与指教.
1 王竹溪.热力学(第2版).北京: 北京大学出版社,2005.420~421, 94
2 汪志诚.热力学统计物理(第4版).北京:高等教育出版社,2008.265~270
3 吴义彬.玻尔兹曼因子方法打开了精确计算分子相互作用特性的大门.物理通报,2016(2):99~103
4 吴义彬.实际气体的玻尔兹曼因子方程.江西科学,2011,29(1):11
5 卡尔L·约斯.MATHESON气体数据手册.陶鹏万,黄建彬,朱大方译.北京:化学工业出版社,2003.432
6 К·П·雅阔夫列夫.简明物理技术手册(第1卷). 黄镜权,尤烈之译.北京:中国工业出版社,1966. 386,458
7 钱尚武,章立源,李椿.热学(第2版).北京:高等教育出版社,2008.24
