三体问题一类特解的研究

姜付锦

(武汉市黄陂一中 湖北 武汉 430300)

(收稿日期：2016-04-08)



三体问题一类特解的研究

姜付锦

(武汉市黄陂一中 湖北 武汉 430300)

(收稿日期：2016-04-08)

采用等效质量的方法对三体问题中3个天体始终构成一个正三角形的特解进行研究，得到了其运动的轨迹方程和运动周期的解析解.

三体问题 等效质量 解析解

宇宙中由3个天体构成的系统，忽略其他天体对它们的作用时存在一种运动形式：3个天体在相互之间的万有引力的作用下，分别位于等边三角形的3个顶点上，绕其一共同圆心在三角形所在平面内做曲线运动.本文先研究了3个天体做匀速圆周运动的规律，后研究一般轨道上的运动规律.

1 三体做匀速圆周运动

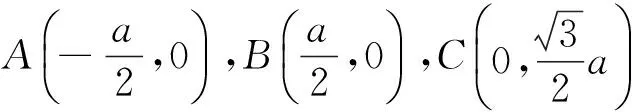
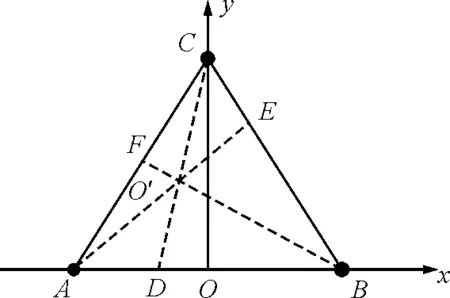
图1 三体做匀速圆周运动

A，B星系统的质心为D在x轴上坐标为

设A，B，C 3天体的质心为O′，则O′在CD的连线上，C天体做匀速圆周的半径为

同理可求得天体A和B的轨道半径分别为

C做匀速圆周运动过程中受到的万有引力的合力为

F=

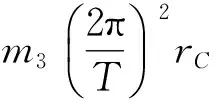
三体若始终构成一个边长不变的正三角形，则系统的周期与边长和三体的总质量有关.

2 三体的一般轨道

若用等效质心法,则3个天体一定组成一个正三角形，质心位置不变.

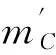
代入F和rC可求得

同理得

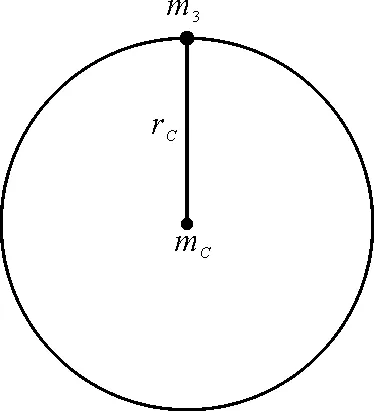
图2 三体等效质量的计算

在图3中，令中心天体的等效质量为M，某一个天体的质量为m，则星体与中心天体的作用力可写为

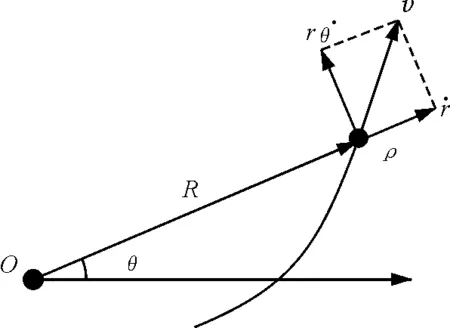
图3 三体的一般轨道

由比耐公式[2]

代入后得

即

这个微分方程形式与谐振动方程完全一样，它的解为

ξ=Acos(θ-θ0)

而

即

三体问题中的某一个天体的轨道方程可写为

式中

其中θ0与初始位置有关.

当E<0时，则e<1轨道为椭圆;

当E>0时，则e>1轨道为双曲线;

当E=0时，则e=1轨道为抛物线.

说明:

(1)要保证3个天体始终组成一个正三角形，则3个天体运动轨迹的离心率应相等.

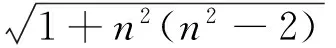
3 三体问题的周期

设A是矢径扫过的面积，由开普勒第二定律，知单位时间内矢径扫过的面积相等，即

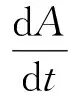
即

或

将上式两边积分后得

2A=h(T-t0)

当矢径扫过全部椭圆后，A=πab，而所需的时间就是周期T，2πab=hT，整理后得

即

整理为

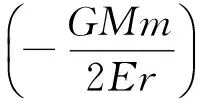
实际运动中能量为NE0，即

当N>0时，则e<1轨道为椭圆;

当N<0时，则e>1轨道为双曲线;

当N=0时，则e=1轨道为抛物线.

4 数值模拟

为了研究问题的方便，令G=1,m1=1,m2=2,m3=3,数值模拟如图4所示.

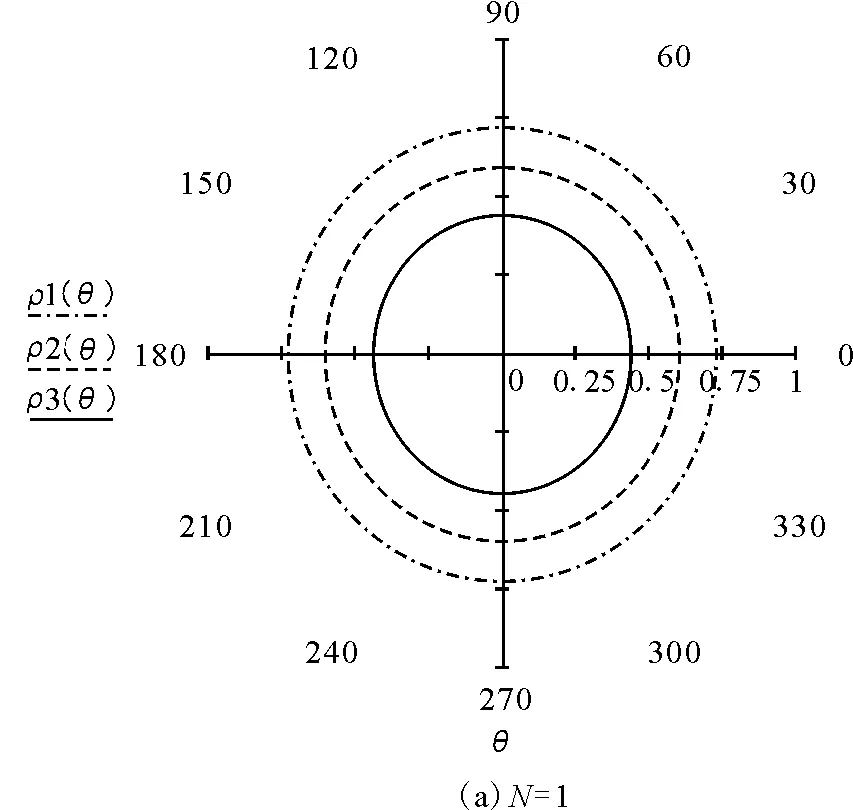
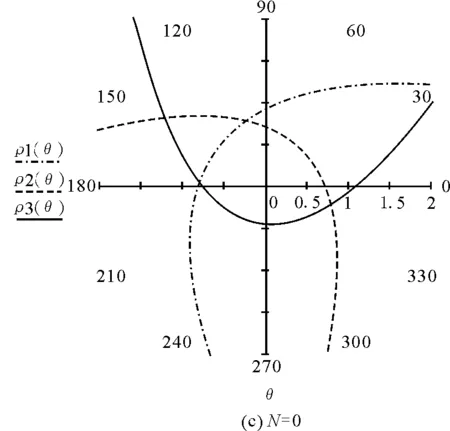
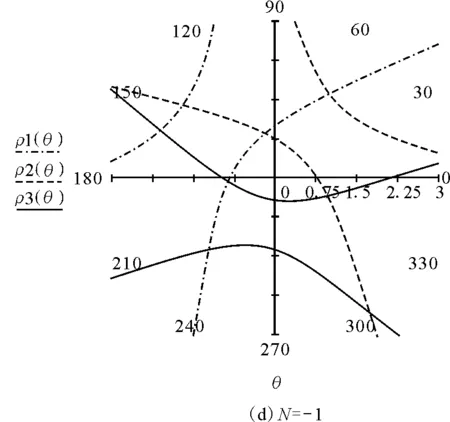
图4 三体运动轨道的数值模拟

5 结束语

通过对三体问题此类特解的分析可以发现，三体的运动轨道和周期与它们初始状态有关，比如能