具有隔离策略的网络病毒传播模型周期解*

宋利民，张子振

(1. 聊城教育学院计算机系，山东聊城 252004；2. 安徽财经大学管理科学与工程学院，安徽蚌埠 233030)



具有隔离策略的网络病毒传播模型周期解*

宋利民1，张子振2

(1. 聊城教育学院计算机系，山东聊城 252004；2. 安徽财经大学管理科学与工程学院，安徽蚌埠 233030)

研究一类具有隔离策略的时滞SIQR网络病毒传播模型的动力学行为.以杀毒软件查杀网络病毒所需要的时间周期时滞为分岔参数，给出模型局部渐近稳定的充分条件，并确定了模型产生Hopf分岔的时滞临界点.利用中心流形定理和规范型理论推导出确定模型周期解性质的显性计算公式.最后给出仿真示例，验证了所得理论结果的正确性.

SIQR 模型； Hopf分岔；稳定性；周期解

引言

随着互联网和信息技术的发展，互联网的应用越来越广泛.与此同时，互联网的应用也给网络病毒的传播提供了诸多途径，给互联网用户带来巨大的损失.因此，如何研究网络病毒传播规律并有效控制网络病毒的传播，成为目前研究的热门课题.考虑到网络病毒在计算机之间的传播和生物病毒在个体之间的传播的共性，Kephart和White[1～2]首次利用SIS传染病模型研究了网络病毒在互联网上的传播规律.随后，国内外不少研究学者提出了许多不同的网络病毒传播模型[3-5].Piqueira和Araujo[3]提出了一类改进的SIR网络病毒传播模型，得到模型局部和全局渐近稳定的充分条件.Gan等[5]提出一类具有免疫和非线性发生率的SIRS网络病毒传播模型，并证明了无病毒平衡点和有病毒平衡点的全局渐近稳定性.

但是，任何网络病毒都有一定的潜伏期，杀毒软件查杀病毒需要一定的时间周期.考虑到网络病毒传播过程中的这些延迟因素，具有时滞的网络病毒传播模型的动力学性质受到国内外研究学者的关注[6～8].杨在文献[6]中提出了下列具有隔离策略的时滞SIQR网络病毒传播模型：

(1)

其中，S(t) ，I(t) ，Q(t) 和R(t) 分别表示易感主机、已感染主机、被隔离主机和处于恢复状态主机在时刻t 的数量；τ为网络病毒潜伏期时滞；p ，b，β，d，δ，α1，γ，ε和α2均为模型(1)的参数，具体意义可以参看文献[6]. 杨[6]研究了模型(1)的全局吸引性和持续性.对于动力学模型而言，其动力学性质，除了全局吸引性以外，还有诸如分岔和周期解等性质.基于此，并考虑到杀毒软件查杀病毒的时间周期，本文研究另外一种情形的时滞SIQR网络病毒传播模型的周期解：

(2)

其中，τ为杀毒软件查杀网络病毒所需要的时间周期时滞.本文主要研究时滞τ对模型(2)稳定性的影响.

1 模型稳定性和Hopf分岔的存在性

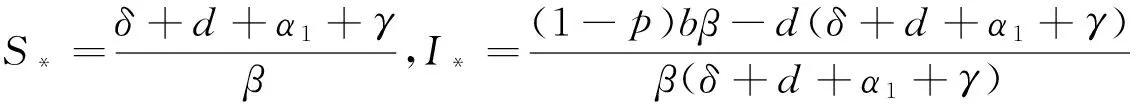
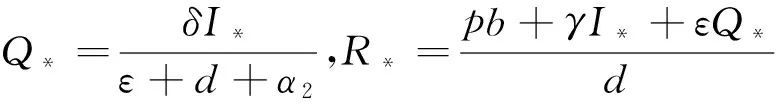
因此，可得模型(2)在正平衡点D*(S*,I*,Q*,R*)处的特征方程为：

λ4+m3λ3+m2λ2+m1λ+m0+(n3λ3+n2λ2+n1λ+n0)e-λτ+(p2λ2+p1λ+p0)e-2λτ=0.

(3)

其中，

m0=(a11a22-a12a21)a33a44, m1=(a12a21-a11a22)(a33+a44)-a33a44(a11+a22),

m2=a11a22+a33a44-a12a21+(a11+a22)(a33+a44), m3=-(a11+a22+a33+a44),

n0=(a11a22-a12a21)a44b33+a11a33a44b22, n1=a12a21b33-b22(a11a33+a11a44+a33a44)-b33(a11a22

+a11a44+a22a44),

n2=b22(a11+a33+a44)+b33(a11+a22+a44),n3=-(b22+b33),

p0=b22b33,p1=-b22b33(a11+a44),p2=a11a44b22b33.

当τ=0时，方程(3)变为

λ4+m03λ3+m02λ2+m01λ+m00=0.

(4)

其中，

m03=m3+n3,m02=m2+n2+p2,m01=m1+n1+p1,m00=m0+n0+p0.

根据Hurwitz稳定性判据可知，如果条件(H1)成立，则当τ=0时模型(2)局部渐进稳定.

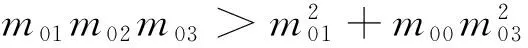
当τ>0时，方程(3)左右两边同时乘以eλτ，方程(3)变为下列形式

n3λ3+n2λ2+n1λ+n0+(λ4+m3λ3+m2λ2+m1λ+m0)eλτ+(p2λ2+p1λ+p0)e-λτ=0.

(5)

令λ=iω(ω>0)为方程(5)的根，得到

(6)

其中，

g1(ω)=(m1+p1)ω-m3ω3,g2(ω)=ω4-(m2+p2)ω2+m0+p0,g3(ω)=n2ω2-n0,

g4(ω)=g1(ω),g5(ω)=ω4-(m2-p2)ω2+m0-p0,g6(ω)=n3ω3-n1ω.

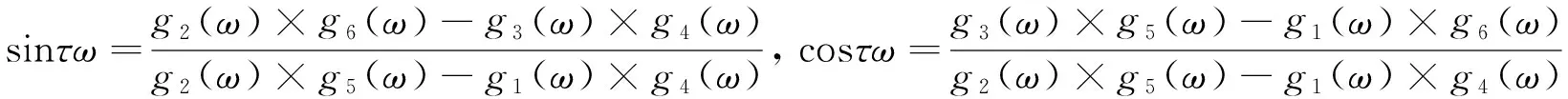
进而可以得到关于ω的下列代数方程

sin2τω+cos2τω=1.

(7)

如果模型(2)的所有参数值给定，则方程(7)的根可以利用Matlab软件直接求得.因此，为了得到本文的主要结果，给出下列假设.

(H2) 方程(7)至少存在一个正实根.

如果条件(H2)成立，则存在ω0>0使得方程(3)存在一对纯须根±iω0.对于ω0有，

对于方程(5)，左右两边同时求λ关于τ的导数，得到

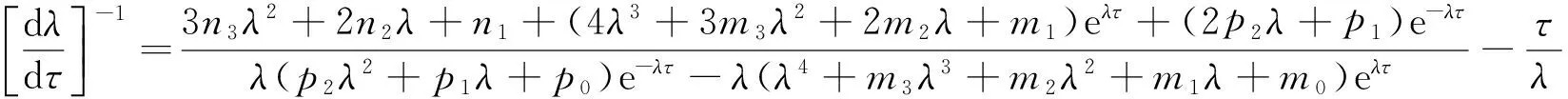
定理1 如果条件(H1)～(H3)成立，则当 τ∈[0,τ0)时模型(2)的正平衡点D*(S*,I*,Q*,R*)是局部渐进稳定的.当τ=τ0时模型 (2) 失去稳定并产生Hopf分岔，并且在D*(S*,I*,Q*,R*)附近产生一簇分岔周期解.

2 模型周期解性质

做下列转换t→(t/τ),u1(t)=S(t)-S*, u2(t)=I(t)-I*,u3(t)=Q(t)-Q*, u4(t)=R(t)-R*,τ=τ0+μ, μ∈R. 则μ=0是模型(2)产生Hopf分岔的临界点，并且模型(2)可以转化为下列形式

(8)

其中，

ut=(u1(t),u2(t),u3(t),u4(t))T∈C=C([-1,0],R4)，

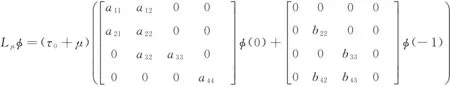
(9)

(10)

根据Riesz表示定理可知，存在有界变差函数η(θ,μ),θ∈[-1,0]使得

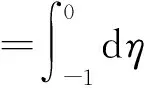
(11)

可以选取

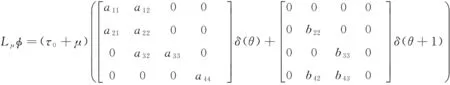
(12)

对于φ∈C([-1,0]),R4)，定义

(13)

和

(14)

则模型(8)可以转化为下列算子方程形式

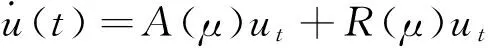
15)

对于φ∈C1([-1,0]),(R4)*)，定义A(0)的伴随算子A*

(16)

以及双线性内积

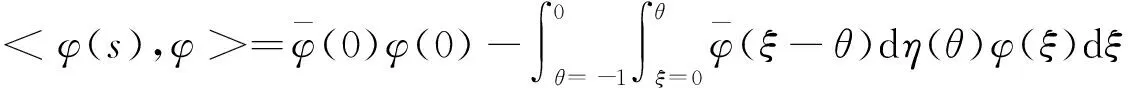
(17)

其中η(θ)=η(θ,0).

根据A(0)和A*的定义，可以计算得到A(0)的对应于+iω0τ0的特征向量ρ(θ)和A*的对应于-iω0τ0的特征向量ρ*(θ),

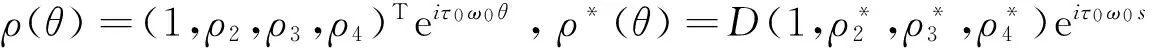
其中，

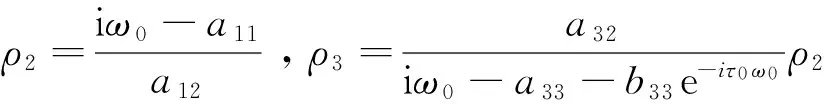
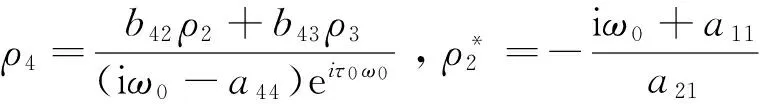
接下来，利用文献[11]中的算法和相似的计算步骤，可以得到下列影响模型(2)的分岔周期解性质的重要参数表达式：

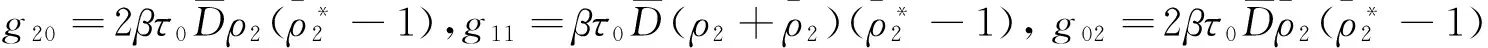
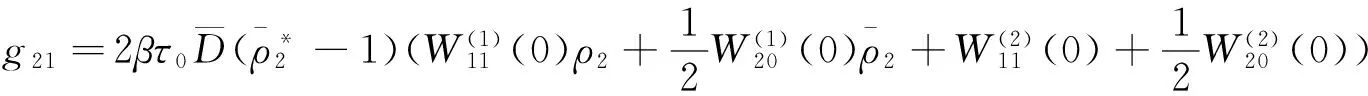
其中，

(18)

(19)

E1和E2的表达式可以由下列方程计算得到:

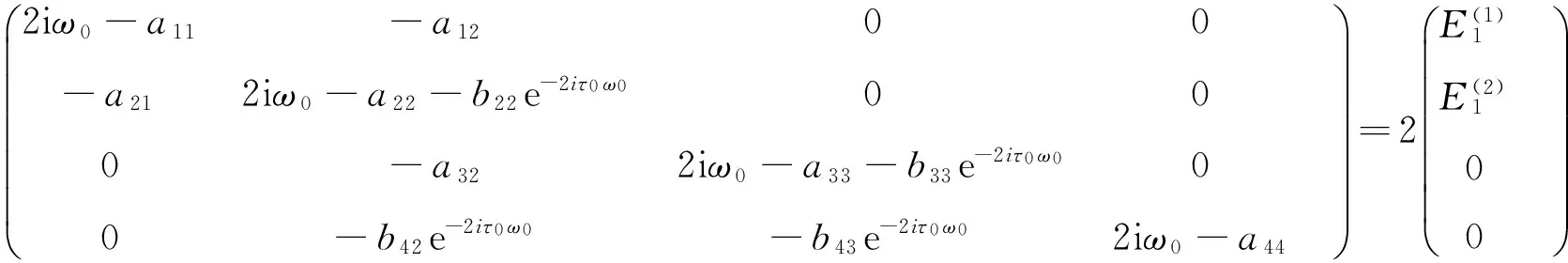
(20)

(21)

其中，

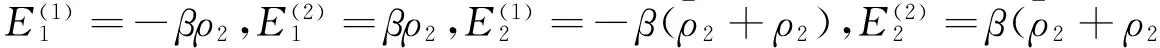
最后，可以计算得到下列参数的表达式：

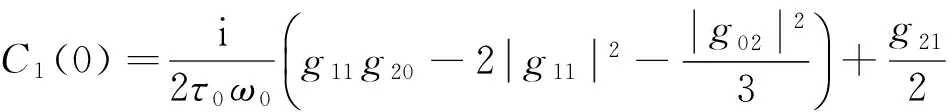
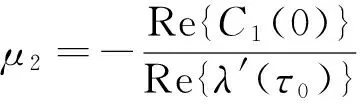
β2=2Re{C1(0)},

(22)

最后，可以得到如下关于分岔周期解的结论.

定理2 对于模型 (2), 如果μ2>0(μ2<0) , 则Hopf分岔是超临界(次临界)的；如果β2<0(β2>0),则分岔周期解是稳定(不稳定)的；如果T2>0(T2<0), 则分岔周期解的周期是递增(递减)的.

3 仿真示例

选取p=0.2,β=0.1, d=0.01,α1=0.01, γ=0.5,δ=0.1, ε=0.1, α2=0.02, b=10得到模型 (2)的下列示例:

(23)

经过直接计算可得R0=129.032 3>1，模型(23)存在唯一正平衡点D*(6.200 0, 12.803 2, 9.848 6,938.646 0). 进而可以验证条件(H1)～(H3)成立.最后，计算得到ω0=1.602 2, τ0=1.785 2.根据定理1，当τ∈[0,τ0=1.785 2)时，模型(23)的正平衡点D*是局部渐近稳定的.仿真效果如图1所示.当τ=τ0时，D*将失去稳定性，并产生一簇分岔周期解.仿真效果如图2所示.

另外，经过计算得到，C1(0)=-82.092 1+16.131 4i，λ′(τ0)=1.870 2+9.325 5i.根据公式(22)可得μ2=43.894 8>0,β2=-164.184 2<0,T2=-148.753 7<0.根据定理2可知，模型(23)在τ0=1.785 2处所产生的Hopf分岔是超临界的，分岔周期解是稳定的并且分岔周期解的周期是递减的.

4 小结

基于文献[6]所提出的时滞SIQR网络病毒传播模型，并考虑到杀毒软件对网络病毒进行查杀时所需要的时间周期，本文研究了另外一种形式的时滞SIQR网络病毒传播模型.以时滞τ为分岔参数，通过分析相应特征方程根的分布情况，给出模型局部渐近稳定和产生Hopf分岔的充分条件，并确定时滞临界点τ0的计算公式.研究表明，当时滞τ取值足够小时(τ<τ0),模型是局部渐近稳定的，此时模型处于理想的稳定状态，便于采取有效措施控制网络病毒的传播.当时滞τ=τ0时，模型将失去稳定性并产生Hopf分岔.此时，网络病毒的传播规律难以把控，很难采取有效措施对网络病毒的传播进行控制.另外，利用中心流形定理和规范型理论对模型的分岔周期解的性质进行了研究，给出了影响分岔周期解性质的参数的详细计算公式.最后，利用仿真示例验证了所得结果的正确性.

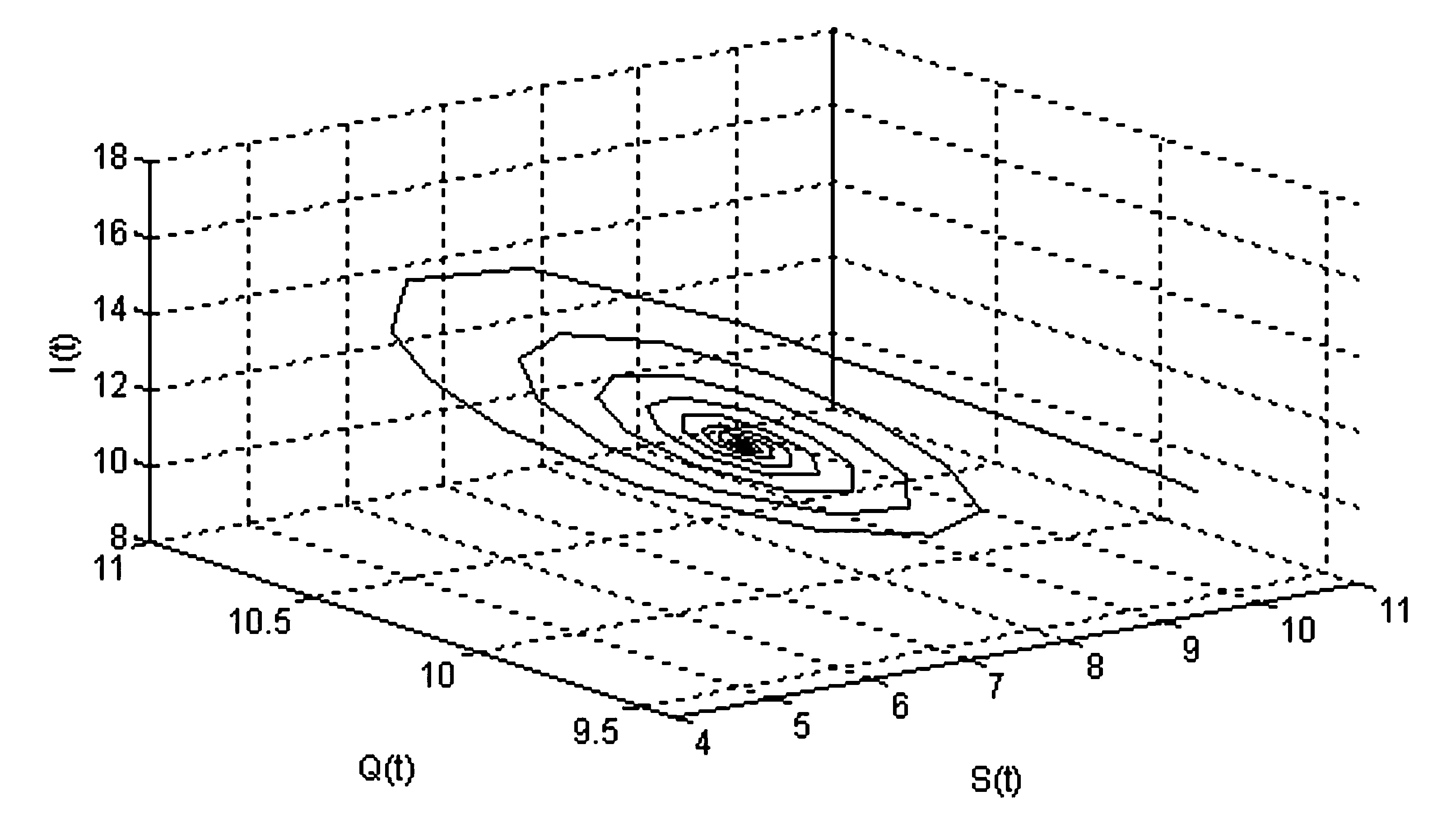
图1 当τ=1.652 7<τ0=1.785 2，初值” 10.05, 10.29, 9.6, 937.665”时模型(23)的相图

图2 当τ=1.853 5>τ0=1.785 2，初值” 10.05, 10.29, 9.6, 937.665”时模型(23)的相图

[1]J.O.Kephart,S.R.White.Measuringandmodelingcomputervirusprevalence[C].in:IEEEComputerSecuritySymposiumonResearchinSecurityandPrivacy,IEEE, 1993, 2-15.

[2] J. O. Kephart, S. R. White.Directed-graph epidemiological models of computer viruses[C]. in: IEEE Symposium on Security and Privacy, 1991, 343-361.

[3] J. R. C. Piqueira, V. O. Araujo.A modified epidemiological model for computer viruses[J].Applied Mathematics and Computation, 2009,213(2):355-360.

[4] H. Yuan and G. Chen.Network virus-epidemic model with the point-to-group information propagation[J].Applied Mathematics and Computation, 2008, 206(1):357-367.

[5]C. Gan, X. Yang,W. Liu, Q. Zhu, X. Zhang.An epidemic model of computer viruses with vaccination and generalized nonlinear incidence rate[J]. Applied Mathematics and Computation, 2013, 222(5):265-274.

[6]杨斌.具有时滞的SIQR计算机病毒模型分析[J]. 重庆工商大学学报(自然科学版),2013, 30(9): 70-73:

[7]L. Feng, X. Liao, H. Li, Q. Han.Hopf bifurcation analysis of a delayed viral infection model in computer networks[J].Mathematical and Computer Modelling, 2012,56(7-8) 167-179.

[8]尹发，张子振，王丽叶.一类时滞SIQRS网络病毒传播模型的稳定性和Hopf分支[J].菏泽学院学报，2015, (5):2327

[9]Hassard B. D, Kazarinoff N. D, Wan Y. H.Theory and Applications of Hopf Bifurcation [M]. Cambridge University Press, Cambridge, 1981.

[11]T. K. Kar, A. Ghorai.Dynamic behaviour of a delayed predator-prey model with harvesting[J].Applied Mathematics and Computation, 2011,217(22):9085-9104.

SIQ Periodic Solution of Network Virus Propagation Model with Isolation Strategy

SONG Li-min1, ZHANG Zi-zhen2

(1.Department of Computer Science, Liaocheng Institute of Education, Liaocheng Shandong 252004, China;2. School of Management Science and Engineering, Anhui University of Finance and Economics, Bengbu Anhui 233030, China)

The dynamic behavior of a delay SIQR network virus propagation model with isolation strategy is studied. First, taking time periodic delay to network virus killing anti-virus software as the bifurcation parameter, sufficient conditions for local asymptotic stability of the model is given, and the delay critical point of Hopf bifurcation is determined. Then, by using the center manifold theorem and the normal form theory, the explicit formula for determining the periodic solution of the model is derived. Finally, a simulation example is given to verify the correctness of the theoretical results.

R model; Hopf bifurcation; stability; periodic solution

1673-2103(2016)05-0056-07

2016-06-20

安徽省自然科学基金项目(1608085QF151)

宋利民(1982-)，男，山东聊城人，讲师，研究方向：计算机网络安全.

O175.12

A