一个带休眠期反应扩散模型常数平衡解的全局稳定性*

王双明，王国兴

(兰州财经大学信息工程学院，甘肃兰州730020)



一个带休眠期反应扩散模型常数平衡解的全局稳定性*

王双明，王国兴

(兰州财经大学信息工程学院，甘肃兰州730020)

对一个带休眠期的反应扩散模型建立了Lyapunov泛函，由此得到了其常数平衡解的全局渐近稳定性．

休眠期；反应扩散模型；常数平衡解；Lyapunov泛函

引言

近些年，数学方法被广泛应用于研究生物现象，并产生了一些新的学科，如种群生物学、传染病学等．在诸多数学方法中，反应扩散方程不仅考虑种群之间的相互作用，还考虑到了在其生存环境中的随机扩散，因此较常微分方程能够更加精确地刻画所要研究的实际问题．对于种群生物学而言，不论采用何种模型，其中一个核心问题是研究模型对应系统解的长时间行为[1,2]．而平衡解的稳定性一直以来备受关注，其处理方法也有很多种．对于常微分方程模型或带时滞的常微分方程模型，最常用方法之一是建立对应于平衡点的Lyapunov函数来判断平衡点的稳定性[3,4]．对于反应扩散方程而言，则须找到相应的 Lyapunov泛函，这在非特殊情形下是一个比较困难的问题．K．Hattaf[5]介绍了一种基于对应常微分系统建立反应扩散系统Lyapunov泛函的方法．本文将利用该方法对一个带休眠期的反应扩散模型建立Lyapunov泛函，研究该模型常数平衡解的全局稳定性．

1 带休眠期反应扩散模型及预备知识

Hadeler和Lewis[6]介绍了单种群模型：

(1)

此模型描述在移动期与休眠期更替的单种群增长，且只有移动期的个体可以繁殖．模型 (1)可以典型地描述干旱气候下生活在小池塘中的无脊椎动物的增长．u(x，t)和v(x,t)分别表示t时刻位于空间位置x处移动和休眠两个亚种的密度．D>0表示可活动种群的扩散系数，γ>0和β>0分别表示两个亚种之间的相互转化率，f为再生函数．Zhang和Zhao[7]分别在无界区域和有界区域上研究了模型(1)的动力学行为．Zhao和Wu[8]研究了模型(1)的二维空间离散模型，得到了严格单调递增的具有一定波速的行波解，并研究了参数对于系统动力学行为的影响．本文将在有界域Ω⊂RN(N≥1)上考虑模型

(2)

的长时间行为．对函数f作出如下假设：

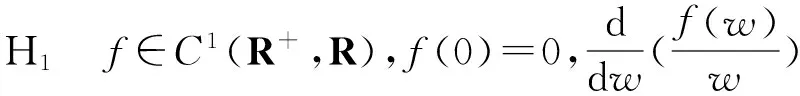
H2存在常数L>0，使得f(w)≤0，∀w≥L.

显然，H1是严格次齐次性假设，且有f(w)0．

引理1[6]假设H1和H2成立，对于任意的φ=(φ1,φ2)∈C(Ω，R+)×C(Ω，R+)，系统(2)有唯一的解(u(x，t，φ)，v(x，t,φ))，∀t≥0，且满足u(·，0，φ)=φ1(·)，v(·，0，φ)=φ2(·)．

由假设H1和H2可知，如果f′(0)≤0，f(w)=0只有一个零点w=0；如果f′(0)>0，f(w)=0有唯一一个正常数解w=K≤L.于是有如下结论成立．

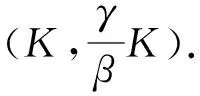
引理3f′(0)>0时，V(u(t)，v(t))是系统(2)对应的常微分系统

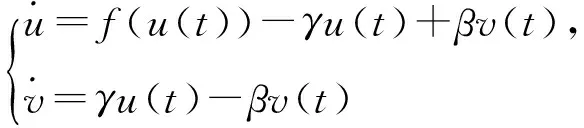
(3)

(4)

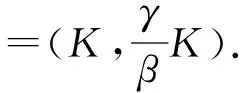
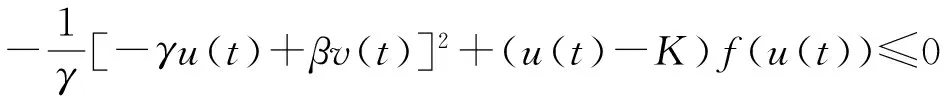
(5)

2 主要结果

本节通过构造Lyapunov泛函来证明系统(1)的两个不同常数平衡点的稳定性．以下两个定理中，始终假设H1和H2是成立的．

证明 建立泛函：

L(u，v)=∫ΩV(u(x，t)，v(x，t))dx

(6)

∫Ω[(u(x，t)-K)(DΔu+f(u(x,t)-γu(x,t)+βv(x,t))+

∫Ω(u(x,t)-K)DΔudx+

D∫Ω(u(x，t)-K)Δudx+∫ΩV(u(x,t),v(x,t))·g(u(x,t),v(x,t))dx.

(7)

式(7)中：

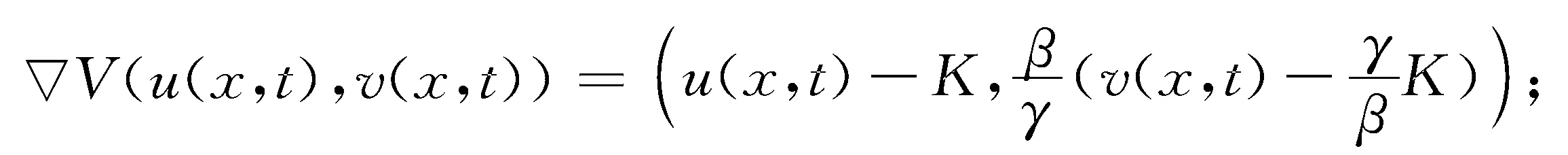
g(u(x,t),v(x,t))=(f(x,u)-γu(x,t)+βv(x,t),γu(x,t)-βv(x,t)T.

利用Green公式和Neumann边界条件，可以得到：

D∫Ω(u(x，t)-K)Δudx=

-D∫Ω(u(x，t)-K)

-D∫Ω(u(x，t))udx=-D∫Ω|u|2dx≤0

(8)

由引理3知，当f′(0)>0时，则：

∫ΩV(u(x,t),v(x,t))·g(u(x,t),v(x,t))dx≤0

(9)

定理2 当f′(0)≤0时，系统(2)的唯一平衡点(0，0)是全局渐进稳定．

证明 建立泛函：

L0(u,v)=∫ΩV0(u(x,t),v(x,t))dx

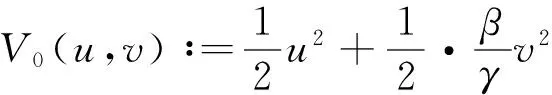
-D∫Ω|

-D∫Ω|

-D∫Ω|

(10)

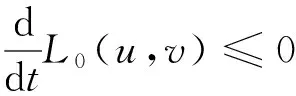
从定理1和2不难发现，只要繁殖函数在低密度状态下正向增长(f′(0)>0)，则该种群能够持久生存，并且最终稳定于一个正常数平衡态；若在低密度状态下，繁殖函数为负(f′(0)≤0)，则该种群会最终灭绝．

[1]Zhao X Q. Global attractivity in a class of nonmonotone reaction-diffusion equations with time delay[J]. Can. Appl. Math. Q, 2009, 17(1): 271-281.

[2]王智诚，王双明．一类时间周期的时滞反应扩散模型的空间动力学研究[J].兰州大学学报：自然科学版，2013,49(4)：535-540．

[3]McCluskeyCC.GlobalstabilityforanSIRepidemicmodelwithdelayandnonlinearincidence[J].NonlinearAnalysis:RealWorldApplications, 2010, 11(4): 3106-3109.

[4]ZhangL,SunJW.GlobalStabilityofaNonlocalEpidemicModelwithDelay[J].TaiwaneseJournalofMathematics, 2016, 20(3): 577-587.

[5]HattafK,YousfiN.Globalstabilityforreaction-diffusionequationsinbiology[J].Computers&MathematicswithApplications, 2013, 66(8): 1488-1497.

[6]HadelerKP,LewisMA.Spatialdynamicsofthediffusivelogisticequationwithasedentarycompartment[J].CanadApplMathQuart, 2002, 10:473-499.

[7]ZhangKF,ZhaoXQ.Asymptoticbehaviourofareaction-diffusionmodelwithaquiescentstage[J].ProceedingsoftheRoyalSocietyA:Mathematical,PhysicalandEngineeringScience, 2007, 463(2080): 1029-1043.

[8]ZhaoHQ,WuSL.Wavepropagationforareaction-diffusionmodelwithaquiescentstageona2Dspatiallattice[J].NonlinearAnalysis:RealWorldApplications, 2011,12(2): 1178-1191.

[9]LaSalleJP.Thestabilityofdynamicalsystems[M].Philadelphia:SIAM, 1976.

The Global Asymptotic Stability of a Reaction-diffusion Model with a Quiescent Stage

WANG Shuang-ming, WANG Guo-xing

(School of Information Engineering, Lanzhou University of Finance and Economics, Lanzhou Gansu 730020, China)

The Lyapunov functional is established for a reaction diffusion model with a resting stage, and the global asymptotic stability of the constant equilibrium solution is obtained.

quiescent stage; reaction-diffusion model; constant equilibrium solutions; Lyapunov functional

1673-2103(2016)05-0036-04

2016-05-18

王双明(1987-),男，甘肃天水人，讲师，硕士，研究方向：偏微分方程、动力系统.

O175

A