A一类三种群时滞捕食系统模型*

马仁雪，谢伟杰，李佳倩，江 月

(安徽财经大学 管理科学与工程学院，安徽蚌埠 233030)



A一类三种群时滞捕食系统模型*

马仁雪，谢伟杰，李佳倩，江 月

(安徽财经大学 管理科学与工程学院，安徽蚌埠 233030)

研究了一类三种群时滞捕食系统模型的稳定性.以食饵种群的消极负反馈时滞为分支参数，利用特征值方法，得到系统模型局部渐近稳定的充分条件并确定了模型产生Hopf分支的时滞临界点.最后，利用数值模拟验证了所得结果正确性.

时滞捕食系统；种群；稳定性；Hopf分支

引言

考虑到自然界中种群之间的复杂关系，近年来多种群捕食系统模型受到国内外研究学者的广泛关注.Kar和Batabyal研究了一类两个食饵种群和一个捕食者种群的系统模型持久性和稳定性[1].Farajzadeh等人则研究了一类具有一个食饵种群和两个捕食者种群的竞争捕食系统模型的稳定性[2].文献[3]研究了一类时标上具有阶段结构的三种群捕食系统的周期解.另外，对于具有时滞的多种群捕食系统模型的研究，也取得了很多成果[4～7].文献[7]研究了一类时滞竞争捕食系统模型：

(1)

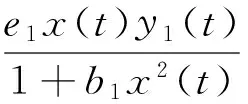
(2)

其中，τ为食饵种群的消极负反馈时滞.

1 局部稳定性分析

b1d1x2-e1x+d1=0.

(3)

(4)

其中，

整理得到：

λ3+A2λ2+A1λ+A0+(B2λ2+B1λ)e-λτ=0,

(5)

其中，

A2=-(a11+a33), A1=a11a33+a12a21+a13a31,

A0=-a12a21a33,B2=-b11,B1=a33b11.

当τ=0时，方程(5)变为

λ3+(A2+B2)λ2+(A1+A1)λ+A0=0.

对于τ>0，令λ=iω(ω>0) 为方程(5)的根，有

(6)

进而

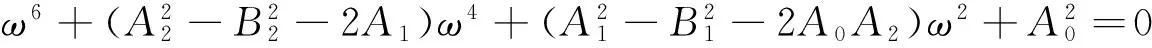
(7)

为了给出本文主要结果，给出下列假设：即(H2) 假设方程(7)至少存在一个正实根ω0. 由方程(6)可得相应的时滞临界值为

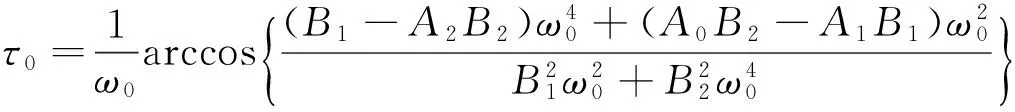
当τ=τ0时，方程(5)具有一对纯虚根±iω0.

对方程(5)两端同时对τ进行求导, 得到

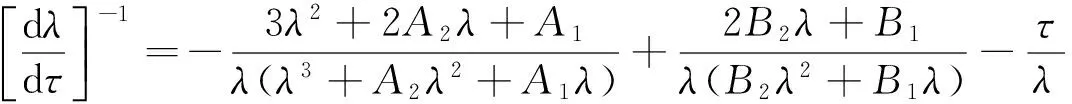
所以,

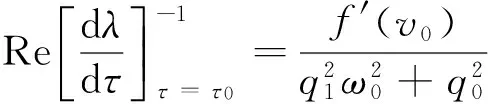
其中,

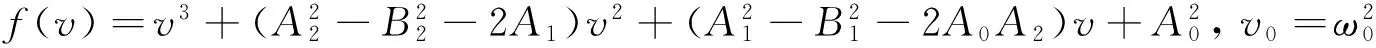
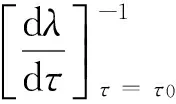
2 数值模拟

为了验证以上所得理论结果，我们给出一个仿真示例.为了方便起见，仍然采用文献[7]中的各参数值：

(8)

经过计算，得到系统(8)有唯一的正平衡点 E*(1.308 4,0.187 6,2.818 1)，并进而得到，ω0=1.307 6, τ0=1.058 2.根据定理1中的结果可知, 当τ∈[0,1.058 2)时， E*(1.308 4,0.187 6,2.818 1)局部渐近稳定，仿真效果如图1所示. 当τ>τ0=1.058 2时，E*(1.308 4,0.187 6,2.818 1)将失去稳定性，并在

E*(1.308 4,0.187 6,2.818 1)附近产生一簇分支周期解，仿真效果如图2所示.

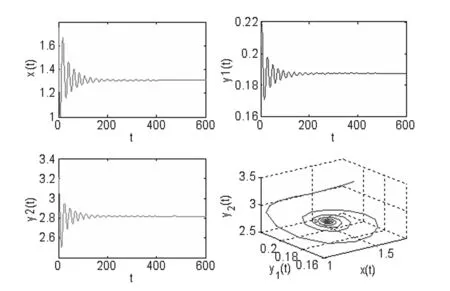
图1: 当τ=0.855<τ0=1.058 2 时，E*渐近稳定

图 2: 当τ=1.125>τ0=1.058 2时E*失稳，并产生Hopf分支

3 结论

本文在文献[7]的基础上，研究了一类具有消极负反馈时滞的的三种群捕食系统模型.相对于文献[7]，本文主要研究食饵种群的消极负反馈时滞对系统模型的影响.研究表明，食饵种群的消极负反馈时滞对模型的稳定性也有一定的影响.当时滞的值低于临界值τ0时，系统模型处于理想的稳定状态.当时滞的值高于临界值τ0时，系统模型将失去稳定性.并且，从仿真示例可以看出，相对于食饵种群的成熟时滞，消极负反馈时滞对模型稳定性的影响要更大一些.因为采用相同的参数值，所得到的消极负反馈时滞临界点要比成熟时滞临界点小的多(成熟时滞临界点可参考文献[7]).

[1]T.K.Kar, A.Batabyal. Persistence and stability of a two prey one predator system [J]. International Journal of Engineering, Science and Technology,2010,2(2):174-190.

[2]徐昌进. 时标上具有阶段结构的三种群捕食系统的周期解[J]. 经济数学, 2013,30(1):5-11.

[3]A. Farajzadeh, M. H. Rahmani Doust, F. Haghighifar, D. Baleanu. The stability of gauss model having one-prey and two-predators [J]. Abstract and Applied Analysis,2012,1(1):1-9.

[4]Cui Guo-hu, Yan Xiang-ping. Stability and bifurcation analysis on a three-species food chain system with two delays [J], Communications in Nonlinear Science and Numerical Simulation, 2011, 16(9):3704-3720.

[5]Meng Xin-you, Huo Hai-feng, Zhang Xiao-bing, Xiang Hong. Stability and Hopf bifurcation in a three-species system with feedback delays [J].Donlinear Dynamics, 2011, 64(4): 349-364.

[6]Meng Xin-you, Huo Hai-feng, Zhang Xiao-bing. Stability and global Hopf bifurcation in a delayed food web consisting of a prey and two predators [J]. Communications in Nonlinear Science and Numerical Simulation, 2011, 16(9):4335-4348.

[7]刘娟. 一类时滞竞争捕食系统模型的Hopf分支[J]. 滨州学院学报,2015,31(4):32-35.

[8]B. D. Hassard, N. D. Kazarinoff, Y. H. Wan, Theory and Applications of Hopf Bifurcation [M]. Cambridge University Press, Cambridge, 1981.

A Class of Three-species Predator-prey System with Time Delay

MA Ren-xue, XIE Wei-jie, LI Jia-qian, JIANG Yue

(School of Management Science and Engineering, Anhui University of Finance and Economics, Bengbu Anhui233030, China)

This paper is concerned with stability of a three-species predator-prey system with time delay. Using the characteristic value method, the sufficient conditions for the local asymptotic stability of the system model are obtained, and the time delay critical point of the Hopf bifurcation is determined. Finally, numerical simulations are used to verify the correctness of the results.

predator-prey system with time delay; species; stability; Hopf bifurcation

1673-2103(2016)05-0032-04

2016-09-20

2016年度安徽省自然科学基金青年项目(1608085QF151)

马仁雪(1997-)，女，安徽寿县人,研究方向：动力系统.

O175.12

A