无穷曲线组上R问题的一般解*

管 珍

(天津职业技术师范大学理学院，天津 300222)



无穷曲线组上R问题的一般解*

管 珍

(天津职业技术师范大学理学院，天津 300222)

以实轴上的Riemann边值问题(以下简称R问题)的解的形式为参照，推广给出有限条无穷曲线上R问题的一般解.

无穷曲线；Riemann边值问题；指标κ

引言

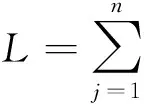
1 实轴上的R问题

考虑一条无穷曲线L上的R问题，不妨将L设作实轴X，即需要求解问题：

Φ+(x)=G(x)Φ-(x)+g(x), x∈X

(1)

这里要求G(x)≠0，并设X的正向与x轴的正向一致，并把x轴的上半平面记为Z+，下半平面记为

Z-，要求Φ(∞)有界.

引理 实轴上的问题Φ+(x)=G(x)Φ-(x)+g(x),x∈X，要求Φ(∞)有界时，若当κ≥0，一般解为：

(2)

若κ=-1，有唯一解：

(3)

总之, 解的自由度为κ+1.

引理的提法及其证明已经在[1]中详细给出，这里我们只提及证明思路.

考虑齐次问题：

Φ+(x)=G(x)Φ-(x),x∈X

(4)

Ψ+(x)=G0(x)Ψ-(x),x∈X

(5)

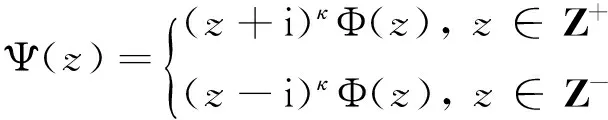
再考虑非齐次问题(1)：

将(1)改写为：

(6)

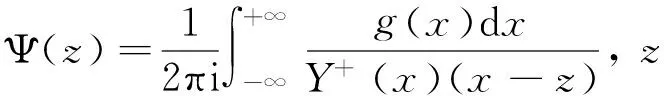
当κ≥0时，F(z)在z=-i处有κ阶.为使它在此处有界，需乘上因子(z+i)κ，则z=∞处它将有κ阶，即有(z+i)κF(z)=Pκ，则Φ(∞)有界时，(1)的一般解是(2).

当κ<0时，F(z)在全平面有界，故为常数C，即Φ(z)=Y(z)[Ψ(z)+C].

当κ=-1时，为了消除z=-i处的极点，只要C=-Ψ(-i)即可，唯一解为(3).

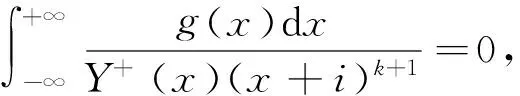
k=1,2,…-κ-1才有唯一解(3).

2 无穷曲线组上的R问题

2.1无穷曲线组上R问题的提法

求解无穷曲线组上的R问题

Φ+(t)=G(t)Φ-(t)+g(t),t∈L

(7)

定理 有线条无穷曲线上的Riemann边值问题(7)，要求Φ(∞)有界时，若当κ≥0，则其一般解为

(8)

当κ=-1时，有唯一解：

(9)

若κ<-1，当且仅当

(10)

满足时，有解，且有唯一解(9). 解的自由度总为κ+1.

2.2 定理的证明

对每一Lj(j=1,2,…n)作问题(7)(限于t∈Lj上)的典则函数Xj(z)，于是，

(11)

且Xj(z)满足典则函数特点Xj(z)≠0于全复平面，在∞处有-κj=-IndLjGj(t)阶.由于各Lj互不相交，故Xj(z)在Lk(k≠j)上全纯[5]，从而

(12)

现在令

(13)

则X(z)是一以L为跳跃曲线的分区全纯函数.由(11)、(12)式可知，

X+(t)=G(t)X-(t),t∈L

(14)

且X(z)≠0于全平面上，包括其边值X±(t)≠0.此外，X(z)在z=∞处的阶数为诸Xj(z)在该处的阶数之和，即

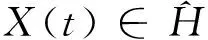
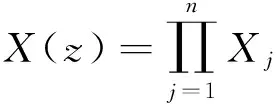
(15)

后，遍乘(x-z1)-κ，使得

(16)

其中无论κ如何，统一令：

(17)

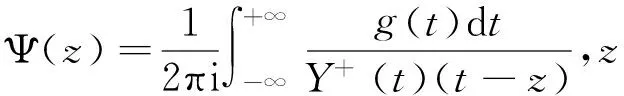
(18)

则(16)式可改写为

(19)

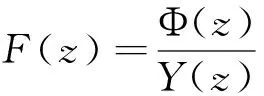
则(7)式在R0中的一般解为：

当κ≥0，一般解

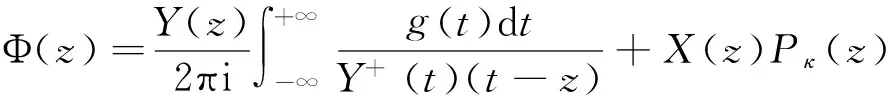
这里利用了(z-z1)-κY(z)=X(z)；

当κ=-1，有唯一解

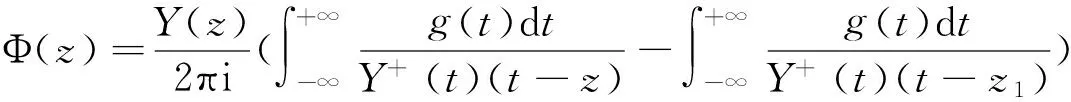
利用了Φ(z)=Y(z)[Ψ(z)-Ψ(z1)]；

当κ<-1，当且仅当满足

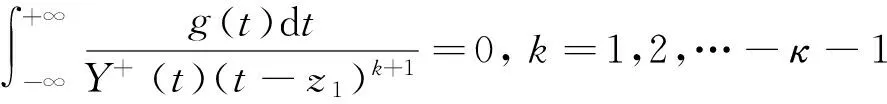
这-κ-1个条件时才有唯一解同(9).

[1]路见可. 解析函数边值问题教程[M]. 武汉：武汉大学出版社. 2009.

[2]路见可. 路见可论文选集[M]. 湖北：武汉大学出版社，1989.

[3]钟寿国. 奇异积分方程的可解条件[J]. 武汉大学学报(数学专辑)，1982,2:120-140.

[4]闻国椿. 共形映射与边值问题[M]. 北京：高等教育出版社，1985.

[5]Mohamed S. Akel, F.Alabbad, A Riemann-Hilbert boundary value problem in a bounded sector [J]. Complex Variables and Elliptic Equations, Vol. 60, No.4, 493-509 (2015).

[6]H.Begehr, Boundary value problems in complex analysis [J]. Bol. Asoc. Mat. Venez, (2005)65-85,217-250.

The General Solution of R Problem on Limited Infinite Curves

GUAN Zhen

(College of Science, Tianjin University of Technology and Education, Tianjin 300222, China)

The paper takes the form of solution of the Riemann boundary value problem(here in after referred to as R) on the real axis as reference to give a general solution of the problem R on limited infinite curves.

infinite curve; Riemann boundary value problem; indexκ

1673-2103(2016)05-0028-04

2016-05-23

天津职业技术师范大学研究生创新基金项目(YC16-13)

管珍(1993-)，女，山西大同人，硕士研究生，研究方向：复分析与复几何.

O175.8

A