关于矩阵的Hadamard积和Fan积的两个估计式

李艳艳

(文山学院 数学学院，云南 文山 663000)



关于矩阵的Hadamard积和Fan积的两个估计式

李艳艳

(文山学院 数学学院，云南 文山 663000)

利用变形的Brauer卵形定理，给出了非负矩阵的Hadamard积的上界估计式和M-矩阵的Fan积的下界估计式，这两个估计式改进了王峰给出的结果.

非负矩阵；Hadamard积；M-矩阵；Fan积；谱半径；最小特征值

矩阵的特征值问题是矩阵理论研究的重要问题之一，因为它在许多学科中都有广泛的应用.在该类问题的研究中，关于特殊的矩阵乘积(Hadamard积和Fan积)的特征值界的估计问题，近年来是一热点问题，许多学者如黄荣、刘庆兵、赵琳琳、陈付彬、王峰等都给出了较好的结果[1-5].

本文继续该问题的研究，给出了非负矩阵的Hadamard积的上界估计式和M-矩阵的Fan积的下界估计式，这两个估计式改进了王峰给出的结果.

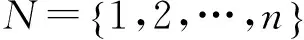
设A=(aij)∈Rn×n，当A的任意一个元素aij≥0，就称A为非负矩阵，记做A≥0，用ρ(A)表示A的谱半径.

设A=(aij)∈Rn×n，当A的非主角元素aij≤0(i≠j)，主对角元素aii>0，并且A-1≥0，就称A为非奇异M-矩阵，用τ(A)表示A的最小特征值.

设A=(aij)∈Rn×n，B=(bij)∈Rn×n，A∘B=(aijbij)，称为矩阵A和B的Hadamard积.

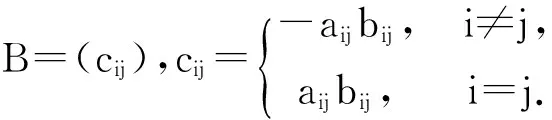
引入一些记号：

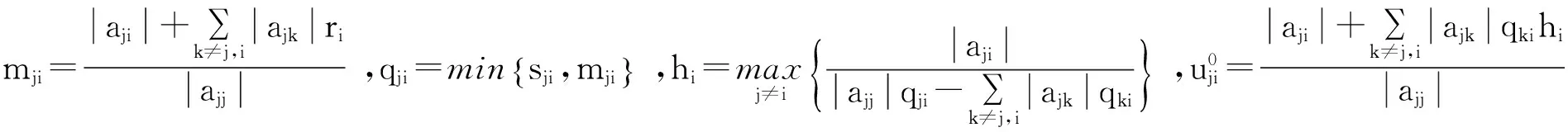
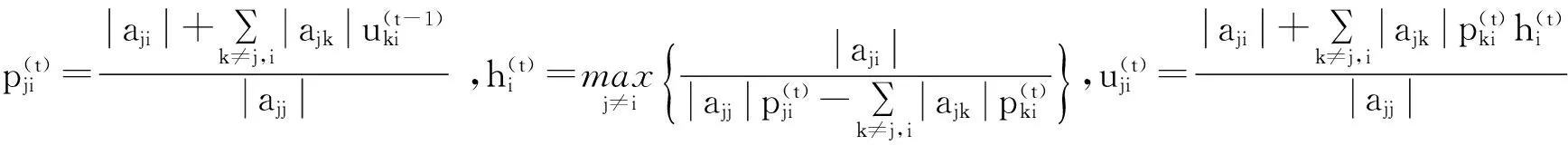
引理1[6]设A=(aij)∈Cn,n，若x1,x2,…,xn是正实数，则A的所有特征值都位于复平面的下列区域中：

本部分主要给出两个结果：非负矩阵Hadamard积的谱半径上界和M-矩阵的Fan积最小特征值的下界.

定理1 设A=(aij)∈Rn,n,B=(bij)∈Rn,n，且A,B≥0,则对任意的i,j∈N，

证明 若n=1，结论显然成立，所以总假设n≥2.

应用引理1中变形的卵形定理，

对该不等式去绝对值化简、整理得:

则该定理得证.

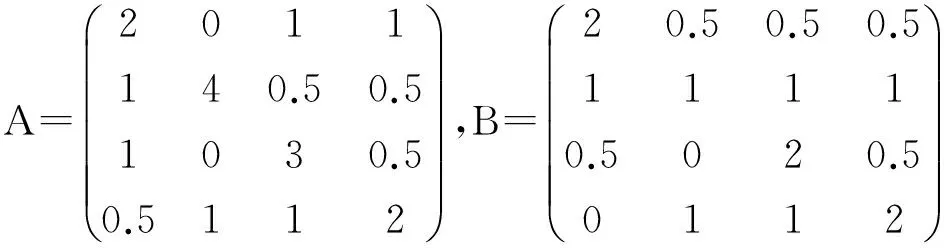
应用文献[5]中的定理1得：ρ(A∘B)≤7.362 0，应用本文定理1，当t=10时，ρ(A∘B)≤6.752 9.事实上ρ(A∘B)=6.336 5.

定理2 设A=(aij)∈Mn,B=(bij)∈Mn，则对任意的i,j∈N，

证明 若n=1，结论显然成立,所以总假设n≥2.

应用引理1中变形的卵形定理，

对该不等式去绝对值化简、整理得:

则该定理得证.

应用文献[5]中的定理2得τ(A*B)≥2.983 2，应用本文定理2，当t=10时，τ(A*B)≥3.057 9.事实上τ(A*B)=3.229 6.参考文献:

[1] HUANG Rong.Some inequalities for the Hadamard product and the Fan produt of matrices[J].Linear Algebra Appl,2008,428(7):1551-1559.

[2] LIU Qing-bing,CHEN Guo-liang.ZHAO Lin-lin.Some new bounds on the spectral radius of matrices[J].Linear Algebra Appl,2010,432(4):936-948.

[3] ZHAO Lin-lin.Two inequalities for the Hadamard product of matrices[J].J Inequal Appl,2012(1):122.

[4] CHEN Fu-bin,REN Xian-hua,HAO Bing.Some new eigenvalue bounds for the Hadamard product and the Fan produt of matrices.

[5] 王峰.矩阵的Hadamard积和Fan积的特征值界的新估计[J].广西师范大学学报(自然科学版),2015,33(3):66-70.

[6] HORN R A,JOHNSON C R.Topics in matrix analysis[M].Cambridge University Press,1995.

责任编辑：时 凌

Two Estimators on the Hadamard Product and Fan Product of Matrix

LI Yanyan

(School of Mathematics,Wenshan University,Wenshan 663000，China)

Using the Brauer ovaloid theorem of deformation,we gave the upper bound of Hadamard product for nonnegative matrix and the lower bound of Fan product forM-matrix.These two estimators improved the results given by Wang Feng.

nonnegative matrix; Hadamard product;M-matrix; Fan product;spectral radius;minimum eigenvalue

2016-07-16.

云南省教育厅科学研究项目(2013Y585).

李艳艳(1987- )，女，硕士，讲师，主要从事矩阵理论及其应用的研究.

1008-8423(2016)03-0307-02

10.13501/j.cnki.42-1569/n.2016.09.016

O151.21

A