异常波动源模型下巨灾标准期权及任选期权的定价
2016-11-29朱丹
朱 丹
(湖南财政经济学院基础课部,中国 长沙 410205)
异常波动源模型下巨灾标准期权及任选期权的定价
朱 丹*
(湖南财政经济学院基础课部,中国 长沙 410205)
从定量的角度分析了巨灾期权的价值构成,并在随机利率下,考虑股票价格异常波动,利用Martingle Pricing方法推导出巨灾标准期权及任选期权定价公式.
巨灾标准期权;任选期权;风险中性定价;波动源模型
“巨灾”是一个随着社会发展而不断变化的新概念,对它至今尚缺乏统一的定性与定量认识.一般从死亡人数、损失金额、影响范围等特点对其加以界定.约定俗成的解释是:“巨灾”是指对人民生命财产造成特别巨大的破坏损失,对区域或国家经济社会产生严重影响的灾害事件,如:地震与海啸、特大洪水、特大风暴潮、特大空难等.
近年来不断攀升的巨灾风险使得传统的保险与再保险体系难以承受损失,为分散风险,传统保险市场不得不与资金雄厚的资本市场结合,由此引发了保险领域的不断创新,衍生了巨灾债券、巨灾期权、巨灾期货等金融新品.
1996年第一支针对保险公司设计的,标的物为普通股票的巨灾股票看跌期权(Cat Put Option)在美国上市.这种巨灾标准期权是以某种约定的股票价格为基础而设计的期权合同,其基本构成要素与价值组成与一般的期权不完全相同,区别在于期权持有者(保险公司)只有在巨灾损失额或灾难次数超过事先规定的某一范围才能行使权力.为更好地吸引投资者,证券市场又相继推出了巨灾指数期权、巨灾飓风指数期权、巨灾任选期权等金融新品.随着各类巨灾风险衍生品的问世,理论界与实务界对其定价问题展开了广泛探讨,对标准巨灾期权的研究比较有代表性的是国外Cox和Robert[1]利用均衡价格理论与无套利定价原理得出的巨灾风险债券定价模型,Hainaut[2]考虑了索赔抵达过程中随机季节性影响,构建了巨灾风险债券定价模型,利用快速傅里叶变换对息票价格进行求解,国内周洪海[3]、龚日朝[4]等利用保险精算原理研究了巨灾指数期权定价模型,李永、刘鹃[5]运用非寿险精算的方法,利用利率期限结构中的BDT模型对台风巨灾债券的损失分布进行了拟合,但这些研究多假定利率为常数且股价服从几何布朗运动.考虑到在市场实践中,当巨灾发生时,股票价格往往会产生异常波动,本文在一种由随机波动源和异常波动源共同作用的股票价格波动模型——波动源模型[6]下探讨巨灾期权定价问题,它既考虑了大量的散户交易者的不相关交易对股票价格造成的随机波动,又考虑到了巨灾产生时对股票价格造成的异常波动,因此,它能更精确地描述巨灾期权对应股票价格的波动现象,更贴近现实市场.
本文在完备市场环境下,假设股票价格服从波动源模型,市场利率为随机利率,利用鞅论及随机微分方程理论,给出了巨灾标准期权及任选期权的价格公式.
1 模型的假设及预备知识
1.1 模型假设
在给定的完备、无套利市场及带流概率空间(Ω,F,P,(Ft)0≤t≤T),总存在唯一的一个风险中性的等价鞅测度,使得市场中任何资产的贴现过程在此测度下为鞅.所以,不妨直接假设P本身即为一个风险中性鞅测度,市场有两种资产:
(1)一种无风险资产,称为债券或银行存款,其价格过程满足方程
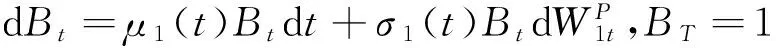
(1)
其中,μ1(t),σ1(t)分别代表在时刻t的瞬间期望报酬率和瞬间标准差,是时间t的非随机函数,Bt=B(t,T)为T时刻到期的零息票债券在时刻t的价格;
(2)另一种是股票,其对应的价格过程{St,0≤t≤T}为波动源模型,满足方程
(2)

1.2 预备知识
为了得到股价波动源模型下巨灾期权在任意时刻t的价值表达式,先引入下面的引理.
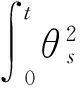
对任意的A∈F都成立,其中EP,EPL分别表示在测度P,PL下的数学期望,I表示示性函数.
引理2[10]设{Nt,0≤t≤T}是参数为λ的Possion计数过程,则对任意实数α,e(αNt+λ(1-eα)t)是P测度下的鞅.
其证明参见[9~10].
由引理2,可考虑将式(2)改写成
(4)
其中,β=λ(1-eα).
2 异常波动源模型下巨灾标准看跌、看涨期权的定价
巨灾看跌期权到期时刻T的价值为:
巨灾看涨期权到期时刻T的价值为:
其中K是约定的行权价格,n是约定的灾难损失额下限值,两者均为定值.
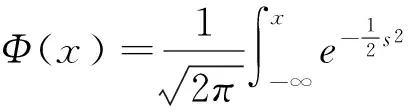
定理1 股价异常波动源模型下,巨灾标准看跌、看涨期权在任意时刻t的价值为:
(5)
(6)
其中τ=T-t.
证 由于P为风险中性测度,故
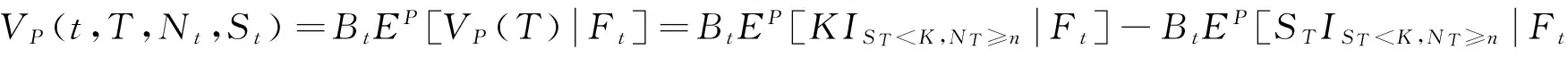
令上式中的第一、二大项分别为V1,V2,先计算V1,为计算方便,选用Bt作为计价单位,定义测度Q,其关于测度P的Radon-Nikodym导数[11]为:

由Girsanov定理,Q是P的等价鞅测度,且如定义

(7)


再计算V2,选取St作为计价单位,定义新测度R,其关于测度P的Radon-Nikodym导数为:
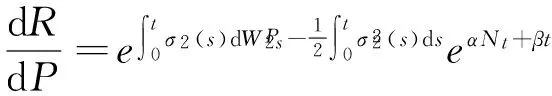
由Girsanov定理,R是P的等价鞅测度,且如定义
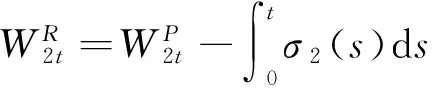
(8)
由Girsanov定理的式(3)及引理2,可得

将V1,V2分别代入,得
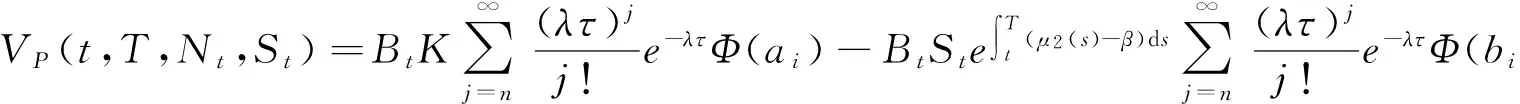
类似计算,可得
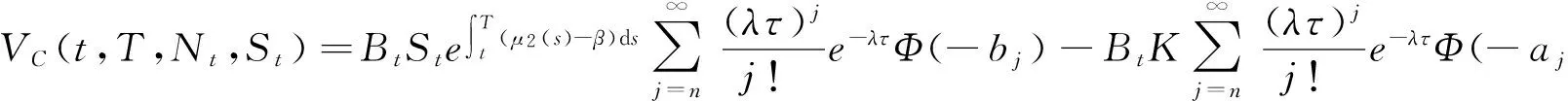
3 异常波动源模型下巨灾任选期权的定价
与标准期权相比,巨灾任选期权事实上是一种复合期权[12],其合约持有人可以在一个事先约定的时间T*(称为选择日)从到期日为T(T*≤T)的看跌和看涨期权中选择一个执行,其规避风险的机会更多,其到期时刻T*的价值为
V(T*,T)=max{VC(T*,T,NT*,ST*),VP(T*,T,NT*,ST*)},
其中,VC(T*,T,NT*,ST*)是巨灾标准看涨期权在时刻T*的价值,VP(T*,T,NT*,ST*)是巨灾标准看跌期权在时刻T*的价值,由定理1,容易得到以下推论,
推论1 在模型(1)和(2)假设下,到期日为T,选择日为T*(T*≤T)的任选期权满足

(9)
则式(9)可化为:
VP(T*,T,NT*,ST*)=VC(T*,T,NT*,ST*)+A1-A2.
(10)
定理2 股价异常波动源模型下,到期日为T,选择日为T*(T*≤T)的巨灾任选期权在任意时刻t(t (11) 其中, 显然,上式中的第一项可看成到期时刻为T,行权价格为K的巨灾标准看涨期权在t时刻的价值,其结果可直接由定理1得到,为 (12) 而第二项可看成到期时刻为T*,行权价格为A1,到期价格为A2的巨灾标准看跌期权在t时刻的价值,其计算为 令上式中的第一、二大项分别为V3,V4,先计算V3,将A1,A2代入,类似于前面V1的计算,将P测度转换为Q测度, (13) 而V4的计算类似于V2,将P测度转换为R测度,可得 (14) 将式(12),(13)和(14)分别代入,即得(11). 本文将无套利定价原理与数学领域的鞅论、随机微分方程理论结合起来,构建一种由随机波动源和异常波动源共同作用的股票价格波动模型——波动源模型,在随机利率下考虑问题,得到了股价异常波动源模型下巨灾标准期权及任选期权的价格公式.做为一种创新金融衍生产品,巨灾期权能为保险公司提供一种新的风险分散机制,也能在巨灾发生时,为投保人减少损失.但是,我国金融市场相对于国外发达国家起步较晚,巨灾期权等保险金融衍生品无论是设计、定价还是运行都缺乏相应的技术支撑,所以再保险市场进展缓慢.不过,作为自然灾害多发的大国,保险市场与资本市场的有效结合是大势所趋,研究巨灾期权以及其他巨灾衍生金融产品的定价问题无疑具有重要的理论及实践价值.本文对巨灾期权定价问题做了初步探讨,期望能对我国金融市场提供一些有益借鉴. [1] COX H,ROBERT G.Insurance futures and hedging insurance price risk[J].J Risk and Insur,1992,59(4):628-644. [2] HAINAUT D.Seasonality modelling for catastrophe bond pricing[J].Bull Fra d’Act,2012,12(5):129-150. [3] 周洪海.基于跳-扩散过程的重置巨灾看跌期权定价[D].乌鲁木尔:新疆大学,2008. [4] 龚日朝,颜 元,刘 玲.巨灾保险模式及保费厘定方法研究[J].南华大学学报(自然科学版),2011,25(2):37-44. [5] 李 永,刘 鹃.基于无套利利率模型的台风巨灾债券定价研究[J].预测,2010,29(1):49-53. [6] 郑晓阳,官 畅.随机参数股价波动源模型下可赎回可转债定价[J].哈尔滨工程大学学报,2011,32(1):124-128. [7] STEVEN S.Stochastic calculus and finance[M].New York: Springer,1997. [8] 朱 丹,杨向群.有跳-扩散违约风险的可转换券的鞅定价[J].数学学报,2010,53(1):165-170. [9] BLACK F,SCHOLES M.The pricing of options and corporate liabilities[J].J Polit Econ,1973,81(May-June):637-659. [10] COX H,FAIRCHILD J,PEDERSEN H.Valuation of structured risk management products[J].J Math Econ,2004,34(2):259-272. [11] 严加安.鞅与随机积分引论[M].上海:上海科学技术出版社,1981. [12] 许聪聪,王建锋.股票价格服从指数O-U过程的复合期权定价方法探析[J].湖南师范大学自然科学学报, 2015,38(3):74-79. (编辑 HWJ) The Pricing for the Catastrophe Option and Chooser Option under Stock Price Fluctuation ZHUDan* (Department of Basic Courses,Hunan College of Finance and Economics,Changsha 410205,China) In this article,the value composition of the Catastrophe option is discussed in quantitative analysis.Under stochastic interest,we consider the models of fluctuation of stock price and obtain the pricing formula of Catastrophe common option and Catastrophe chooser option by means of Martingle approach (risk-neutral valuation). catastrophe option; chooser option; risk-neutral valuation; models of fluctuation of stock price 10.7612/j.issn.1000-2537.2016.05.015 2015-12-31 湖南省软科学基金资助项目(2011ZK3101);湖南财政经济学院科研项目(K201101) *通讯作者,E-mail:dzhu2000123@sina.com O211.63 A 1000-2537(2016)05-0083-06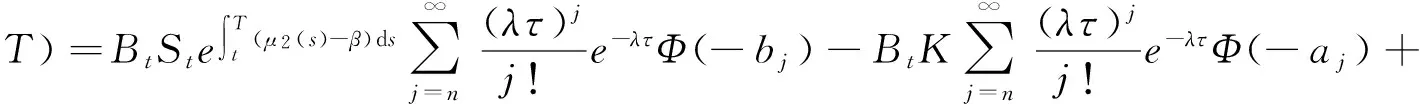



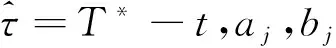
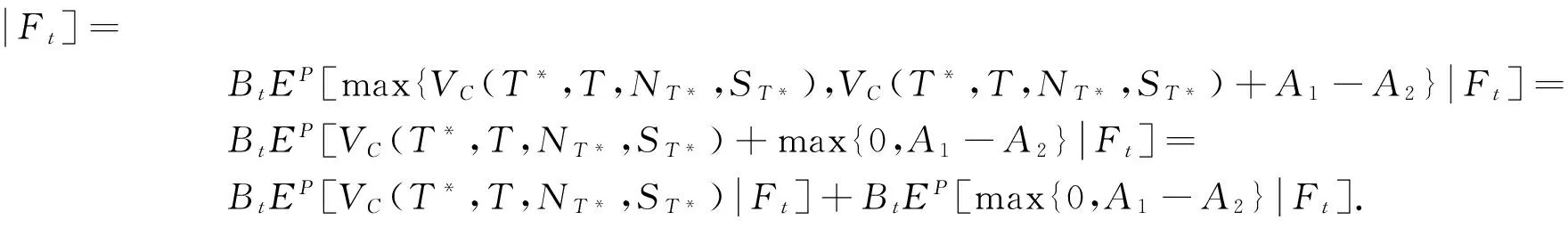
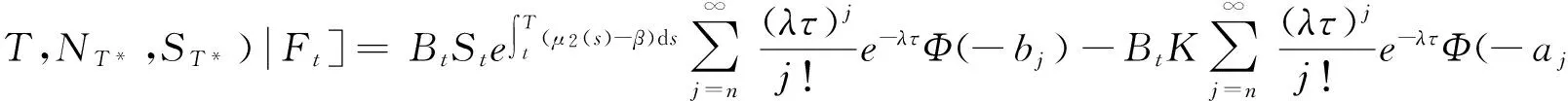
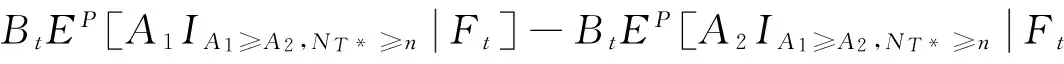
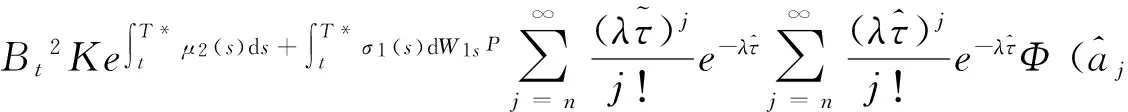

4 结语
