能量回馈型超声波电动机的结构设计与特性分析

王光庆，高帅帅，李萧均，杨斌强

(浙江工商大学，杭州 310018)



能量回馈型超声波电动机的结构设计与特性分析

王光庆，高帅帅，李萧均，杨斌强

(浙江工商大学，杭州 310018)

为解决极端封闭环境中微机器人检测精密驱动及其电子设备自供电问题，提出了一种具有振动能量采集功能的超声波电动机。电机定子由两组压电陶瓷和金属基体构成锥面夹心结构，一组压电陶瓷利用逆压电效应将电能转换成机械振动能，实现电机的精密驱动与定位；另一组压电陶瓷利用正压电效应将定子机械振动能采集转换成电能，实现对电子器件自供电。对电机定子结构和压电陶瓷极化分区模式进行了设计，利用有限元分析软件建立了电机定子结构有限元机电耦合模型，仿真分析了电机振动模态、谐响应、输入导纳特性、能量采集转换特性和阻抗匹配特性等。研究结果为实现基于压电转换的驱动和能量采集一体化机电产品提供理论基础。

振动能量采集；超声波电动机；有限元；结构设计与分析

0 引 言

如何对工作在极端恶劣环境(如密封、有毒、高低温等)中的设备进行检测与控制是近年来困扰工业界的一个重要难题。微型机器人由于不需要人类的干预与操控等优势成为解决该问题的首选，并广泛应用于上述极端恶劣环境中[1-2]。然而，当前大部分工作在极端恶劣环境中的微型机器人的能源动力均为有限能源，这严重影响了微型机器人的工作寿命，一旦有限能源耗尽，机器人将无法继续工作。因此，向极端环境中工作的微型机器人提供可持续的能源是机器人技术领域迫切需要解决的关键问题之一。另外，目前机器人关节机构大都采用电磁电机辅助减速机构的驱动控制方式，这种驱动方式增加了系统的复杂性与控制成本。

超声波电动机(以下简称USM)是一种新型原理与结构的微型特种电机。它是利用压电材料的逆压电效应将电能转换成弹性体的机械振动能，并通过摩擦接触传递运动与力矩。它打破了迄今为止由电磁效应获得转速和转矩的电机的概念，是当今世界高新技术之一[3-4]。超声波电动机具有结构简单、低速大力矩、快速响应、自锁力大、无电磁干扰等优点，可以直接驱动机器人关节机构[5]。然而，超声波电动机的运行机理决定了其整体运行效率低，这对有限能源场合工作的机器人来说无疑是个软肋。因此，如何将超声波电动机的运行过程中的振动能量回收转换成有用的能源，实现为密封、恶劣等极端环境中工作的机器人供电，是一项非常有现实意义的研究工作。

本文提出一种能量回馈型超声波电动机，研究这种超声波电动机的结构设计和振动特性与能量转换特性，为研制出更具有实用价值、集驱动与发电功能一体化的新型超声波电动机打下基础，实现对微型机器人的精密驱动和供电一体化，为微型机器人在极端环境中的广泛应用提供能源和动力保障。

1 电机总体结构设计

考虑到超声波电动机是振动电机，为了能更好地将电机运行过程中的振动能量采集回收，借鉴主流结构环形行波型超声波电动机本体结构，设计的能量回馈型超声波电动机结构如图1所示。能量回馈型超声波电动机主要包括锥面转子和压电定子两大部分，锥面转子通过紧固螺钉固定在输出轴上，并通过端盖、推力轴承的作用力，使之与压电定子的锥面接触。

图1 能量回馈型超声波电动机结构

压电定子结构如图2所示，它通过其基座上的四个螺钉孔安装固定在底座上。压电定子由激振压电陶瓷环、能量采集压电陶瓷环和带锥面齿的金属弹性体通过高强度粘结胶高温固化构成，其中能量采集器压电陶瓷环位于压电定子顶部、金属弹性体位于压电定子中间、激振压电陶瓷环位于压电振子的底部，三者构成夹心式结构。金属弹性体内侧为锥面，与转子锥面配合后形成摩擦驱动接触面。

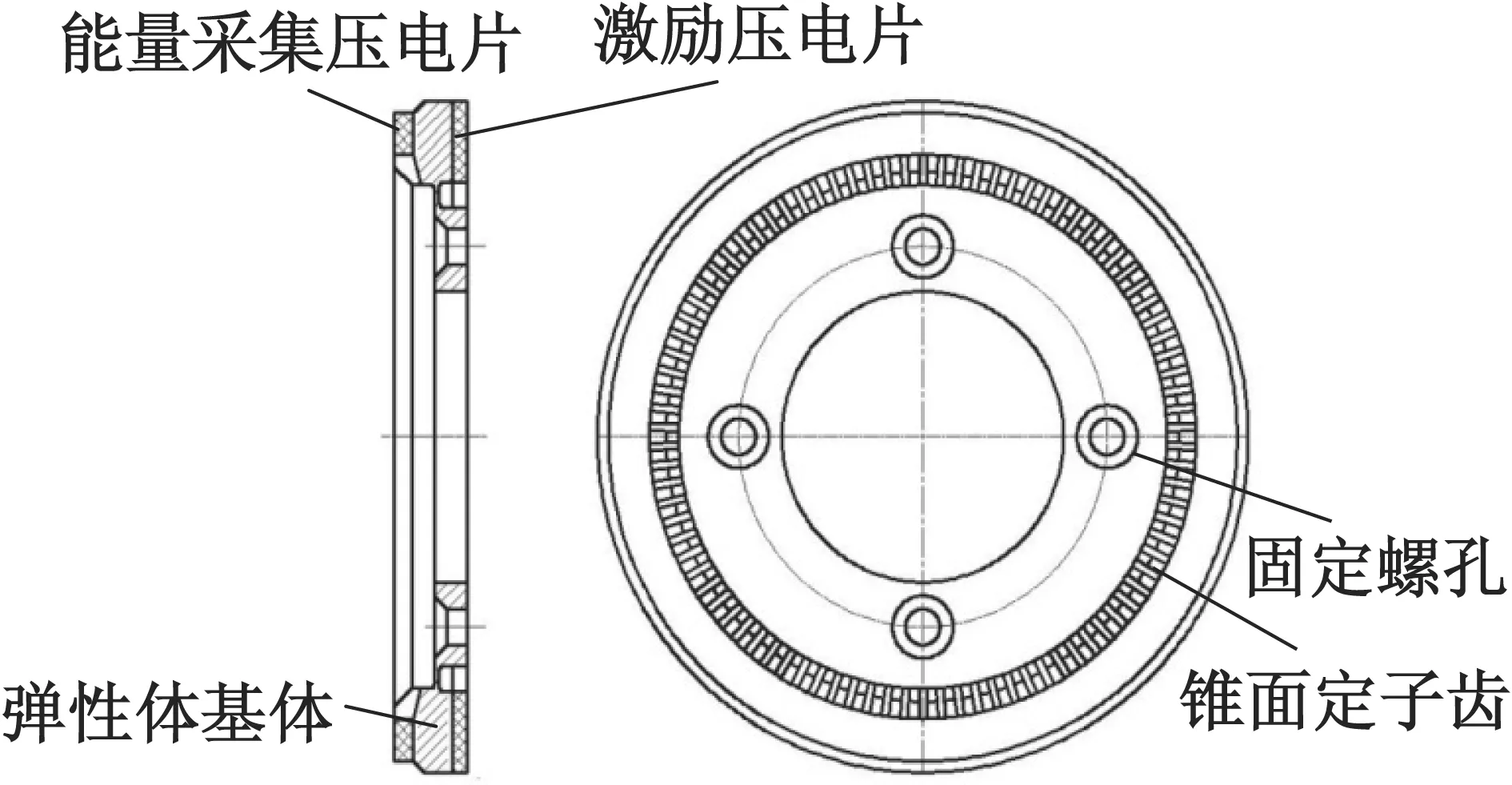
图2 压电定子结构示意图

电机压电陶瓷环的极化分区模式如图3所示。激励压电陶瓷环采用主流环形行波型超声波电动机压电陶瓷极化分区模式[6]，如图3(a)所示，整个激励压电陶瓷被极化分成两个左、右区16个扇区，当压电陶瓷被激励时在定子内部产生9个行波。能量采集器压电陶瓷环的极化分区模式如图3(b)所示，整个压电陶瓷环极化分区成18个扇区，相邻两扇区的极化方向相反。18个扇区可以同时采集定子运行过程中产生的振动能量，将其转换成电能输出。

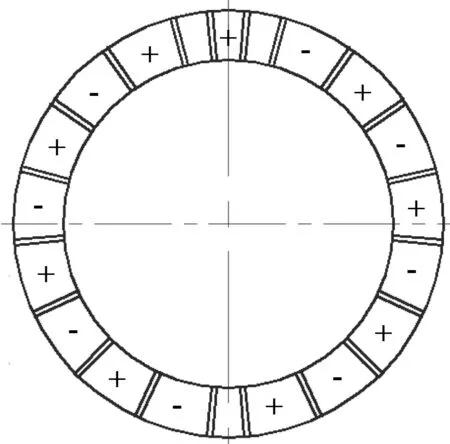
(a) 激励压电陶瓷

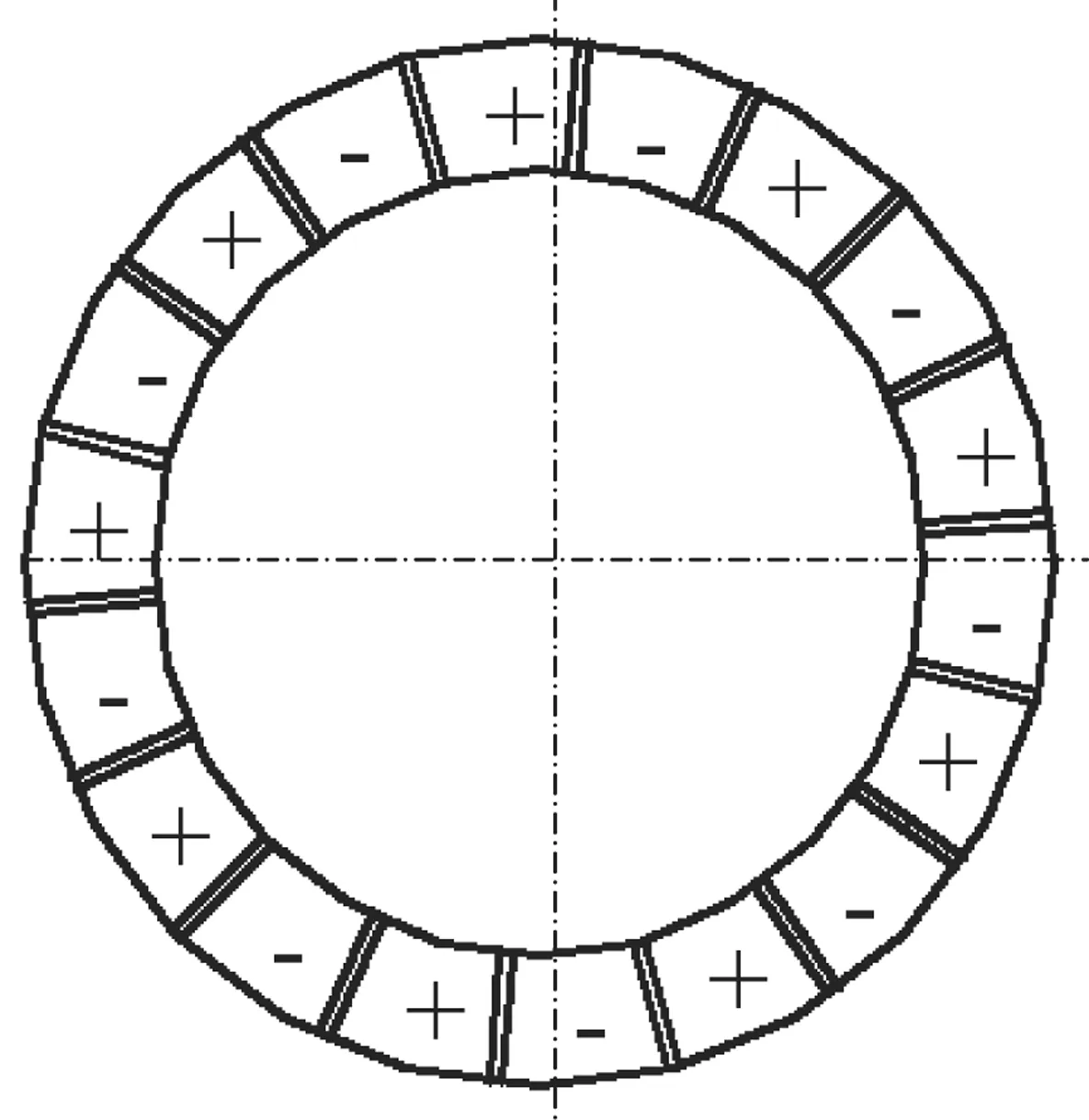
(b) 能量采集压电陶瓷

2 定子锥面结构设计

主流结构环形行波型超声波电动机定、转子摩擦接触面是平面接触，这种接触形式忽略了定子齿顶表面质点径向振动位移的影响。研究证明，径向振动位移与轴向振动位移的幅值一般是一个数量级，会造成较大的径向振动摩擦损耗，不利于提高电机的能量转换效率。因此，能量回馈型超声波电动机采用锥面结构实现定转子间的摩擦驱动[7]，主要是为了充分利用定子齿面质点的径向和轴向振动的合力，使之与接触面垂直，增大接触面的机械振动幅值，减少接触面径向振动的摩擦顺好。因此，锥面结构的设计对定转子摩擦接触转换起到至关重要的作用。图4是锥面结构受力分析图(只画出转子部分)，图中黑粗实线代表锥面定转子摩擦接触结构，Fc表示接触区域内转子受到的预压力，Fr表示其他接触区域对该接触区域施加的作用合力，N为该接触区域定子对转子的支承力，fs为该接触区域内转子受到的静摩擦力，θw为锥面结构锥角。

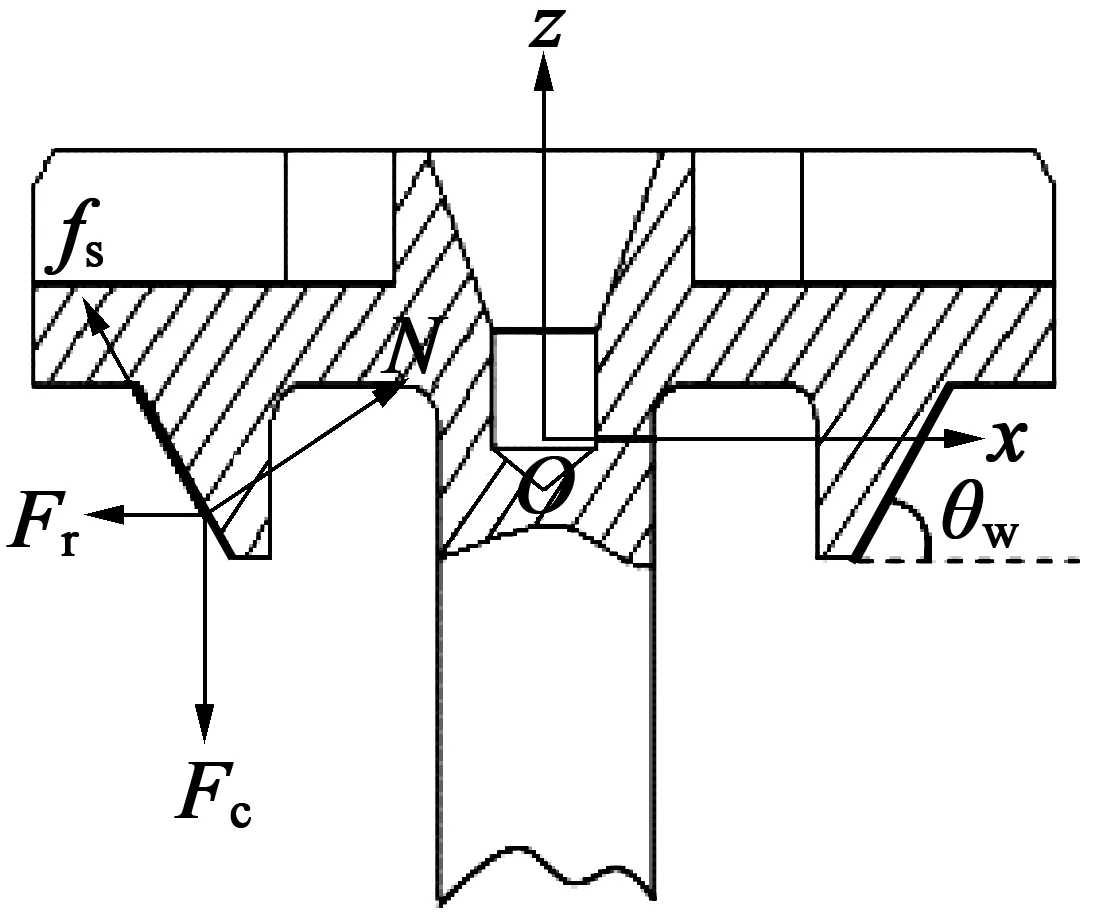
图4 锥面转子结构受力图

假设转子稳定运行时，且定子锥面质点振动方向与转子锥面完全垂直，此时定转子接触面之间不存在径向滑动，由此可以建立转子轴向振动的力平衡方程：

(1)

将fs=Nμs(μs为接触面静摩擦系数)代入上式得到：

(2)

由上式可知， 当θw=0时，式(2)变成：

(3)

此时，定转子接触面变为平面接触形式。

当θw<π/2时，式(2)变成:

(4)

(5)

由式(3)和式(5)可知，要在定转子接触面产生相同的支撑力，锥面接触结构所需的预压力要比平面接触结构小。本文电机定转子锥面静摩擦系数为0.2，则可计算得到锥面结构的锥角θw取值范围为[22.5°,90°]。

3 定子特性分析

3.1 模态分析

根据图2和图4所设计的能量回馈型超声波电动机定子结构，采用有限元方法对其特性进行分析，其中定子弹性体材料为黄铜，压电陶瓷选用无锡海鹰公司生产的PZT-5A，极化方向沿z轴，锥角θw为45°，定子材料和结构参数如表1和表2所示。

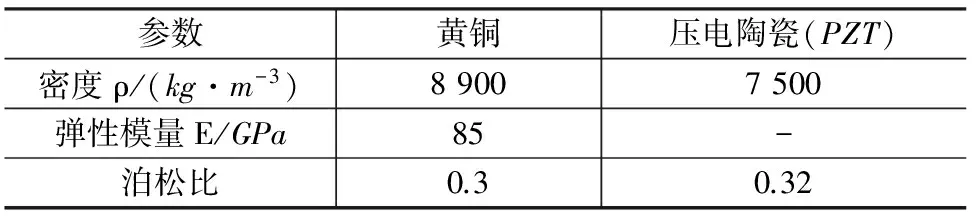
表1 材料参数

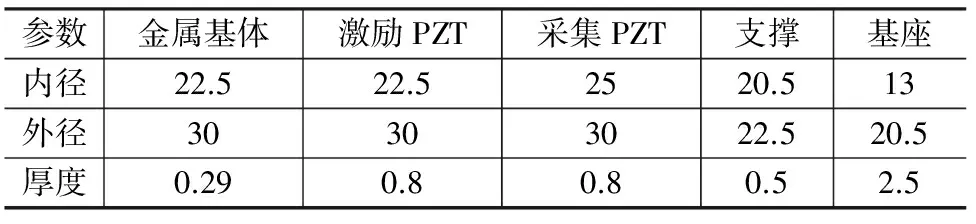
表2 定子结构尺寸 mm

利用有限元分析软件ANSYS10建立电机定子有限元模型[8-9]，压电陶瓷采用8节点六面体耦合场SOLID5 作为单元类型，金属基板采用8节点线性结构SOLID45 作为单元类型。由于压电陶瓷和金属基体之间的粘结层以及PZT表面电极的厚度很小，仅有几十微米到几百微米之间，在ANSYS中属于薄膜结构，使用SHELL63单元作为单元类型。电机定子有限元模型如图5所示。在该模型中对金属基体、PZT等设置单元属性和材料特性，然后，采用“vsweep”命令对定子实体模型进行扫略网格划分。最后，通过“d”命令对基座内径环面进行所有自由度的约束以及对PZT进行节点电压自由度耦合后，计算可以得到电机定子的B0,9模态及其振动频率，结果如图6所示，该模态的振动频率为54.0 kHz。

图5 电机定子有限元模型

图6 电机定子振动模态

3.2 输出特性分析

给定子激励压电陶瓷分别施加两个相位差为90°的正弦电压激励信号，如下：

(1)

式中：Am为电压幅值；f为激励频率。对定子进行扫频分析，扫描频率范围为[50, 60] kHz，定子结构阻尼系数为0.05，提取定子表面节点振动位移响应，其中定子表面节点分布如图7所示， 1，2，3和4分别表示采集压电陶瓷表面节点，5和6表示定子锥面顶点和低点处节点。计算得到上述节点的轴向振动位移和相位响应结果如图8和9所示。由图8和图9可以看出，定子表面振动位移在54 kHz达到最大，这与模态计算分析结果是一致的，采集压电陶瓷表面节点振动位移幅值最大达到1.77 μm，且定子锥面顶部和底部节点振动位移幅值基本保持一致，这有利于提高电机运转的平稳性。

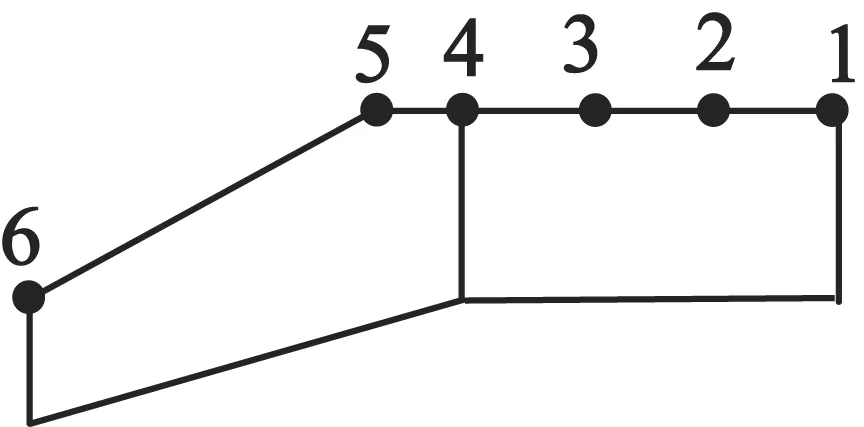
图7 定子表面节点分布情况

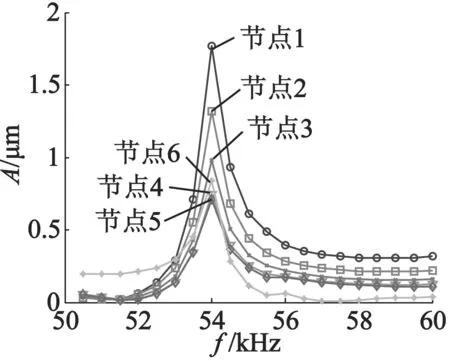
图8 定子节点振动位移响应

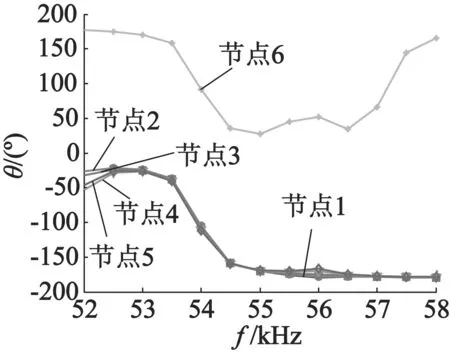
图9 定子节点振动位移相位响应

图10是采集压电片输出电压幅值和相位相应的结果。可以看出，定子在谐振频率54 kHz 处工作时，采集压电片的输出电压达到最大180 V，且相位在此频率处发生改变，由0°改变成-180°。由此可以计算得到采集压电片输出电流和平均输出功率分别：

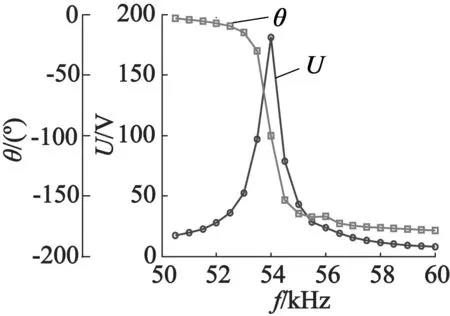
图10 采集压电片输出电压幅值和相位响应曲线

(6)

(7)

式中:f为激励频率；Cp=εrA/hp为采集压电片电容；εr,A和hp分别为采集压电片的介电常数、面积和厚度。计算结果如图11所示。

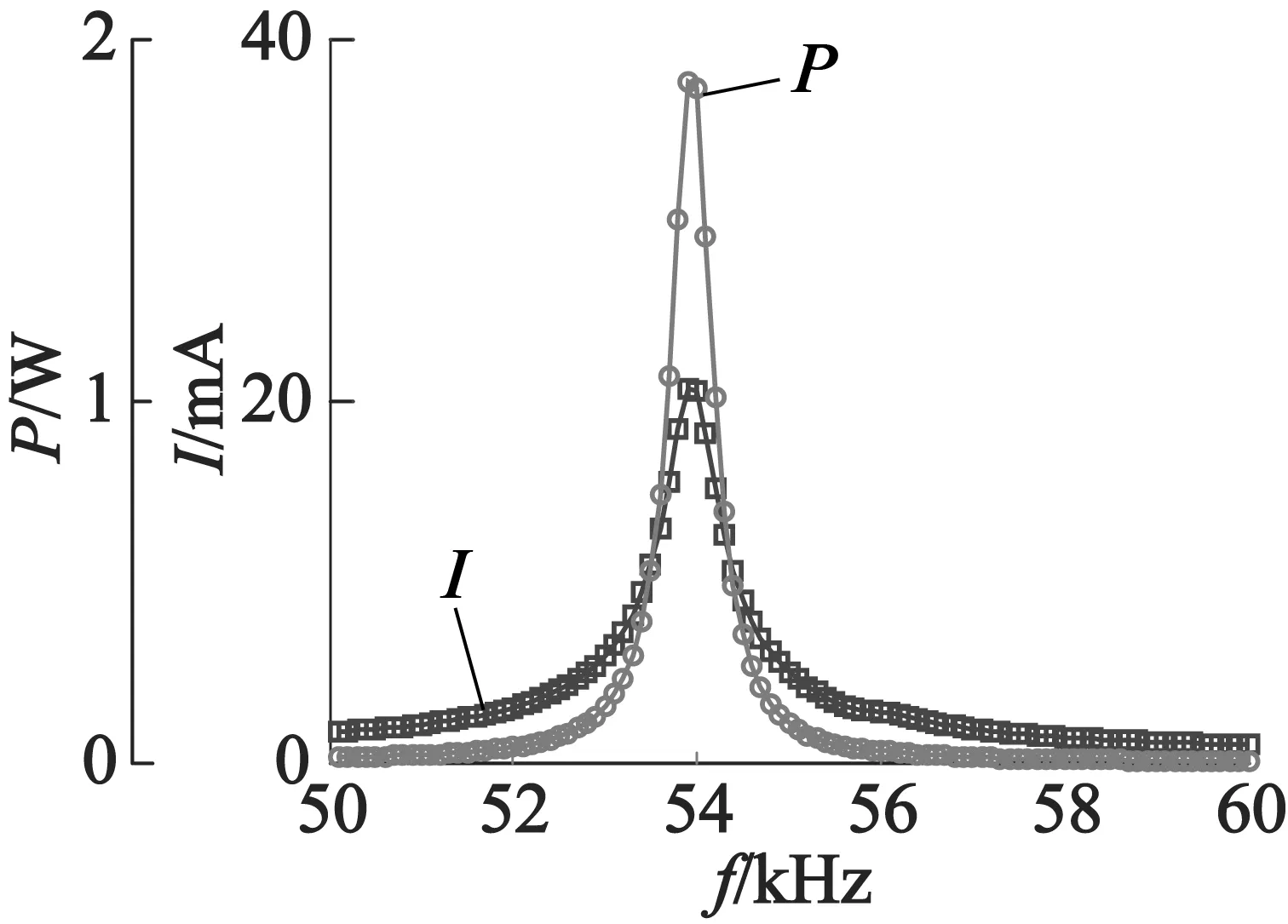
图11 采集压电片输出电流和功率

3.3 输入导纳特性分析

图12是定子激励压电片输入电流和相位响应曲线。可以看出，对于图3(a)的激励压电片极化分区模式，每片激励压电陶瓷的输入电流最大值为0.11 A。根据图12计算得到的输入电流，利用下式可以得到定子激励压电陶瓷的输入导纳特性曲线。

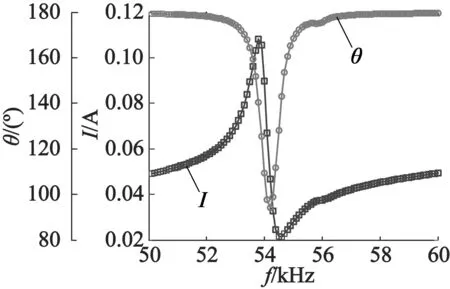
图12 定子输入电流幅值和相位响应

(8)

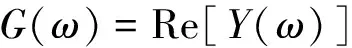
(9)

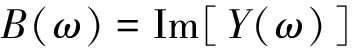
(10)

式中：Y，I和V分别为定子输入导纳、电流和电压；G和B分别为电导和电纳；ω为激励信号角频率。

图13和图14分别是计算得到的定子输入导纳特性曲线和导纳圆。由图13和图14可以得到定子最小导纳频率fm、最大导纳频率fn、串联谐振频率fs、并联谐振频率fp、谐振频率fr等参数。利用这些已知参数对定子等效电路模型参数进行识别，结果如表3所示。

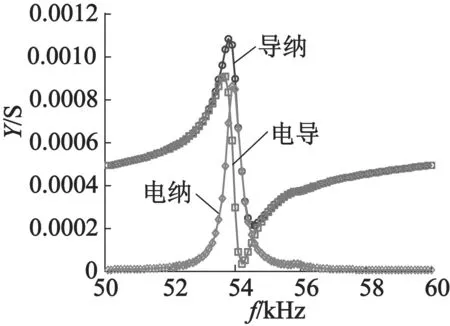
图13 定子输入导纳特性

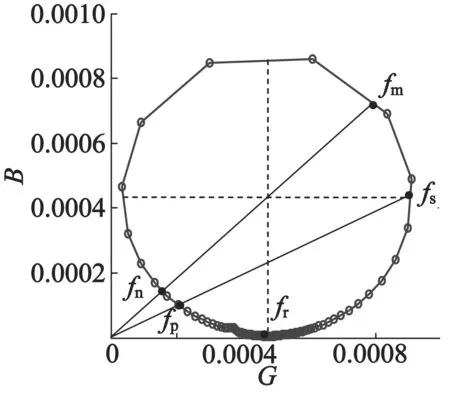
图14 定子输入导纳圆

表3 定子等效电路参数识别结果

3.4 能量采集区阻抗匹配特性分析

为了将采集输出的电能对负载有效供电，需要对负载阻抗与采集压电陶瓷的阻抗进行匹配处理。采集压电陶瓷用一个恒流源I与夹持电容Cp并联连接表示，如图15所示[10]，Z为外部阻抗，V为采集输出电压，IZ为流经阻抗的电流，则外部阻抗的功率：

(11)

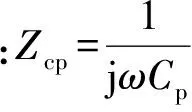
图15 压电陶瓷等效电路图

图16是负载阻抗匹配结果。可以看出，当负载阻抗为9kΩ时，其输出功率达到最大0.7W，此时负载输出功率接近采集压电陶瓷输出功率的50%。

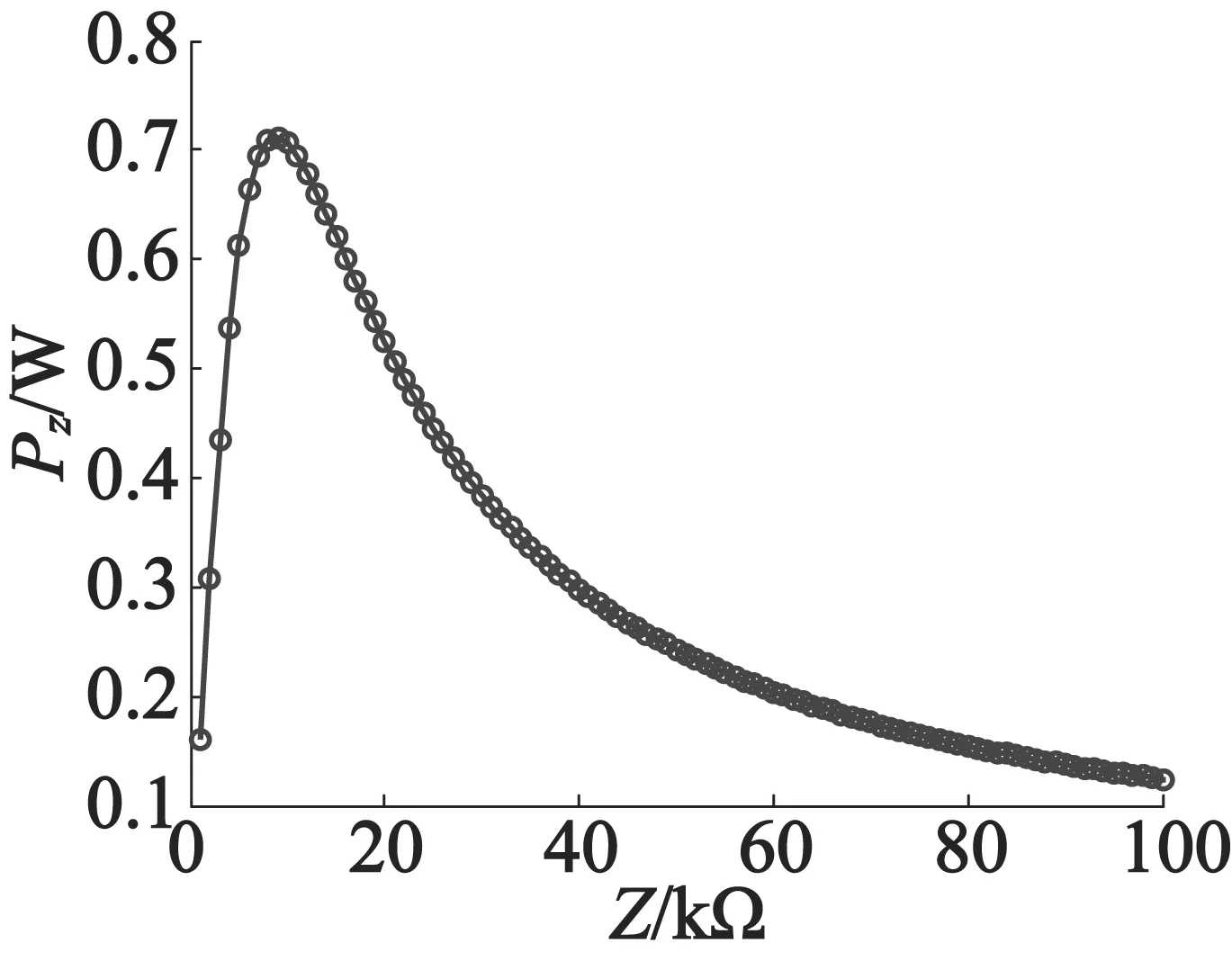
图16 采集区阻抗匹配

4 结 论

本文提出了一种具有振动能量采集功能的超声波电动机，对其结构和特性进行了设计与分析，得到如下结论：

(1) 要在定转子接触面产生相同的支撑力，锥面接触结构所需的预压力要比平面接触结构小；

(2) 锥面接触结构有利于电机运行稳定性，降低定子径向振动损耗；

(3) 电机谐振频率为54kHz，电机振动位移幅值、采集输出电压、电流和输出功率在谐振时达到最大；

(4) 当负载阻抗与采集压电陶瓷阻抗匹配时，负载输出功率达到最大，且为采集压电陶瓷输出功率的50%。

研究结果为能量回馈型超声波电动机样机制作和实验研究提供了理论基础。

[1] 张鹏飞,闫利慧,张珏.管道机器人驱动与控制检测系统设计[J].科技创新导报,2010,(26):15-16.

[2] 穆晓风,顾大强,陈柏,等.血管微型机器人无损伤体内驱动方法[J].浙江大学学报：工学版,2005,39(5):618-622.

[3] 赵淳生.面向21世纪的超声电机技术[J].中国工程科学,2002,4(2):86-91.

[4] ZHAO Chunsheng.Development and application of ultrasonic motors in ihina[C]//2nd International Workshop on Piezoelectric Material and Applications in Actuators (IWPMA),University of Paderborn,Germany,2005:130-138.

[5] SUN Z J,SHUAI S H,HUANG W Q.Control of robot driver by multiple ultrasonic motors based on robust parameter design[J].Transactions of Nanjing University of Aeronautics & Astronautics, 2009, 26(4):243-250.

[6] 王光庆,沈润杰,郭吉丰.压电陶瓷对超声波电动机定子特性的影响[J].机械工程学报,2010,46(4):8-14.

[7] 张东华，陈在礼，陈维山,等. 新型锥面驱动超声电机的实验研究[J].哈尔滨商业大学学报:自然科学版,2006,22(2):58-60.

[8] MOHD ROMLAY F R,WAN YUSOLL W A,MAT PAIH K A.Increasing the efficiency of traveling wave ultrasonic motor by modifying the stator geometry[J].Ultrasonics,2016,64:177-185.

[9] FLUECKIGER M,FERNANDEA J M,PERRIARD Y.Finite element method based design and optimisation methodology for piezoelectric ultrasonic motor [J]. Mathematics and Computers in Simulation, 2010, 81(2):446-459.

[10] 王光庆,陆跃明,郭吉丰.超声波电动机定子振动能量回收转换特性[J].浙江大学学报:工学版,2013,47(1):174-181.

Design and Performances of an Energy-Feedback Type Ultrasonic Motor

WANG Guang-qing, GAO Shuai-shuai, LI Xiao-jun, YANG Bin-qiang

(Zhejiang Gongshang University,Hangzhou 310018,China)

To solve the precision actuate and self-power problems of the micro-robotics operating in an extreme environment, a novel ultrasonic motor with vibration energy harvesting function was proposed. The motor stator consisting of two groups of piezoelectric elements and a metal body is a conical sandwich structure. One piezoelectric element was used to convert the electric energy into mechanical vibration energy with the converse piezoelectric effect, the other piezoelectric element was used to harvest the stator vibration energy and convert it into electric energy with the piezoelectric effect. The structure of the motor and the polarization pattern of the piezoelectric elements were studied, and the electromechanical model of the ultrasonic motor stator was established with the finite element method. The vibration mode, resonant responding, input impedance and the energy harvesting performance were numerically studied. The results provide the theoretical guidance to develop the mechatronics device based on the piezoelectric principle.

vibration energy harvesting; ultrasonic motor; finite element method; structure design and analysis

2015-09-10

国家自然科学基金项目(51277165)；浙江省自然科学基金项目(LY15F10001)；浙江省教育厅项目(Y201223050)；浙江工商大学青年人才计划项目

TM359.9

A

1004-7018(2016)03-0007-04