复杂条件下浅埋隧道围岩压力的非线性上限分析

王张军

（湖南省湘西公路桥梁建设有限公司，湖南吉首 416000）

复杂条件下浅埋隧道围岩压力的非线性上限分析

王张军

（湖南省湘西公路桥梁建设有限公司，湖南吉首 416000）

基于非线性破坏准则和上限定理，分析了浅埋矩形隧道在孔隙水压力和地表荷载同时作用下的稳定性，推导了围岩压力的解析解；采用数学优化方法并编制优化程序，得到了确定参数下围岩压力的上限解。分析结果表明，侧压力系数、初始粘聚力和孔隙水压力系数对围岩压力有较大影响，其他参数也对围岩压力有一定影响；围岩压力随着非线性系数的增大明显增加，采用非线性破坏准则进行隧道及地下工程结构分析更为合理；实际施工中应根据具体工况采取相应支护措施，预防垮塌事故的发生。

隧道；围岩压力；孔隙水压力；地表荷载；上限分析；非线性破坏准则

由于大部分城市隧道处于浅埋地层中，研究浅埋隧道的稳定性并计算相应的围岩压力，对于实际工程设计与施工具有重大意义。谢骏等根据对单圆形隧道破坏机制的分析，构建了黏土层中双平行隧道的破坏机制，研究了隧道间距对其稳定性的影响；杨峰等针对浅埋隧道的破坏特性，构建了两种改进的破坏机制，并通过所得围岩压力与已有结果的对比验证了该破坏机制的有效性；赵炼恒等研究了非关联流动法则下浅埋隧道的稳定性问题，计算结果表明围岩压力受材料剪胀特性的影响较大；李玉峰等分别推导了线性和非线性破坏准则下围岩压力计算公式，并通过实例计算发现岩土体的非线性对围岩压力有较大影响；伍良波等研究了线性破坏准则下浅埋隧道的埋深对围岩压力和稳定系数的影响；程小虎在经典松动围岩压力理论的基础上提出了更为实用的压力公式；周利金考虑孔隙水的影响，针对圆形浅埋隧道进行极限分析，并得到了支护力的上限解。鉴于实际工程中隧道常常受多种荷载的同时作用，该文对浅埋矩形隧道在地表荷载和孔隙水压力作用下的稳定性进行非线性极限分析，推导围岩压力计算公式，同时通过数学优化方法求解围岩压力的上限解，分析各参数对围岩压力的影响。

1 基本原理

1.1极限分析上限定理

极限分析理论最早由Drucker D.C.等提出，随后Chen W.F.通过深入研究，使其成为求解岩土工程上下限解的有效方法。极限分析上限定理可表述为：在任意满足速度边界的速度场中，由能量分析所得到的荷载大于等于实际破坏荷载。如果考虑孔隙水压力的影响，则其表达式为：

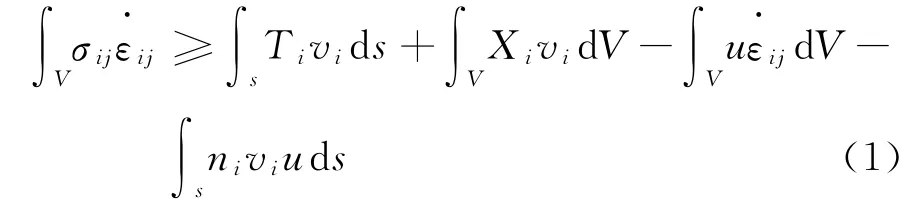
式中：σn、τn分别为破坏面上的正应力和剪应力；c0为初始粘聚力；σt为岩土体单轴抗拉强度；m为非线性系数；c0、σt和m的值可通过试验测得。

在应力空间中，非线性破坏准则在任意一点处的切线方程为：

式中：ct为切线的截距；tanφt为切线的斜率；ct和φt常分别称为切线粘聚力、切线内摩擦角。

式中：σij分别为应力张量和应变率；Ti为边界s上的荷载；vi为速度不连续面上的速度；Xi为体积力；V为变形体的体积；ni为破坏面的外法向量；u为孔隙水压力。

1.2非线性破坏准则

对于实际工程中的岩土体，大量测试试验结果表明，应力空间中其屈服面上的最大主应力与最小主应力呈现一种非线性关系，而常用的线性关系只是其中的一个特例。因此，在岩土工程结构分析中采用非线性破坏准则可更真实地反映岩土体的破坏特征，并得到更准确的结果。非线性Mohr-Coulomb破坏准则为：

联立式（2）和式（3），可得到切线粘聚力与切线内摩擦角的关系：

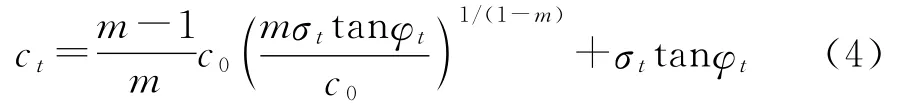
2 破坏机制

根据规范并考虑隧道的实际破坏特征，构建图1（a）所示浅埋矩形隧道的破坏机制，各速度间的矢量关系如图1（b）所示。

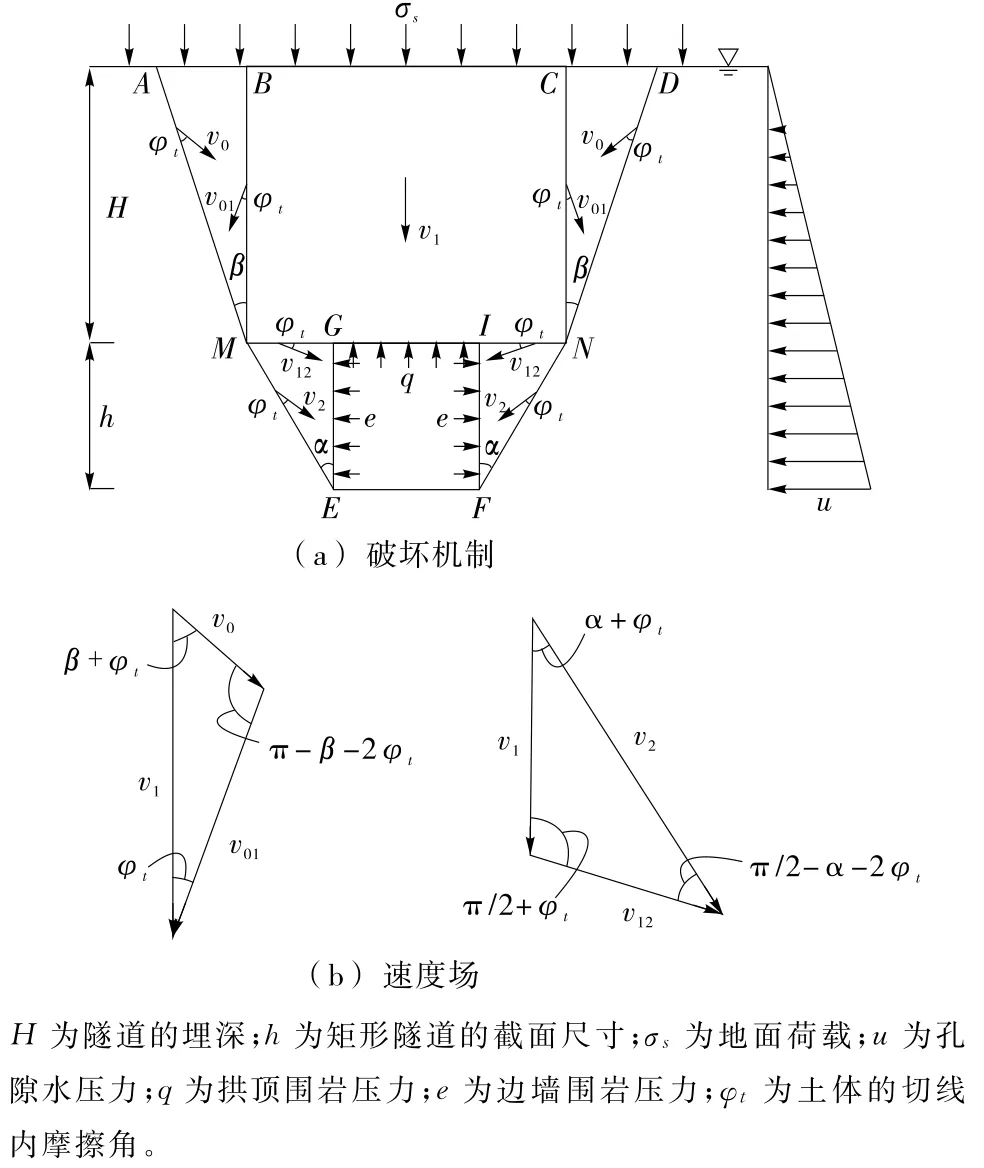
图1　浅埋矩形隧道的破坏机制与速度场

3 极限分析过程

考虑到破坏机制及速度场的对称性，取一半结构进行计算。根据速度矢量关系，得到各速度间的关系如下：

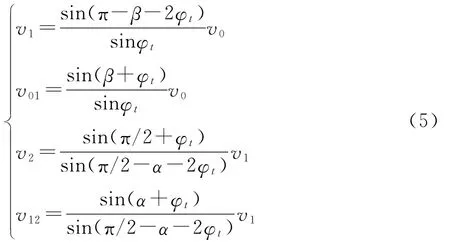
破坏发生时，破坏机制中各刚体的长度和面积可由下式计算得到：

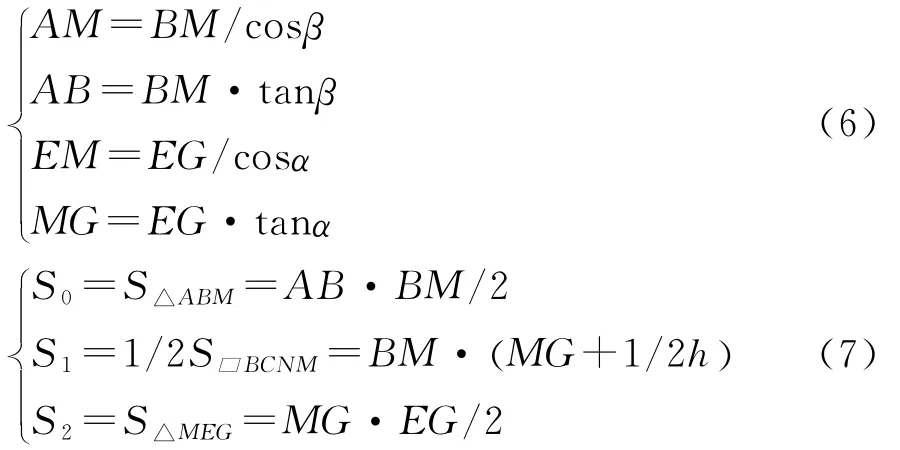
根据式（1），围岩压力的上限解可由外力功率和内能耗散率相等得到，即：

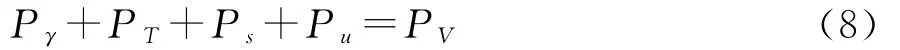
式中：Pγ为土体自重的做功功率；PT为支护力的做功功率；Ps为地表荷载的做功功率；Pu为孔隙水压力的做功功率；PV为岩土体内能损耗率。

这里将破坏体假设为刚体，故当破坏发生时其体积应变率ε·ij为零。根据式（1），孔隙水的做功功率可按下式计算：

根据Michalowski R.L.的研究成果，孔隙水压力可按下式计算：

式中：ru为孔隙水压力系数；γ为土体的单位重度；z为地下水位高度。

综上，可得各功率的计算表达式如下：

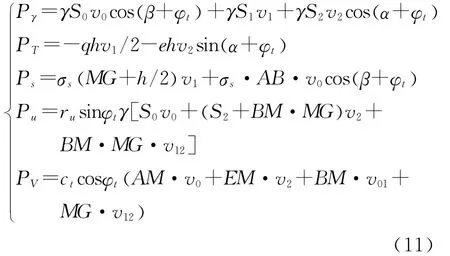
根据式（6）和式（8），得围岩压力的解析解为：

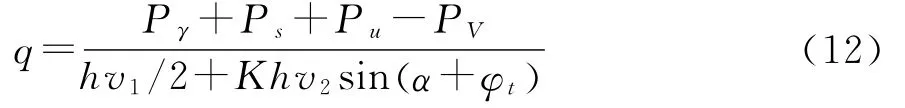
式中：K为侧压力系数。

为了满足破坏机制的几何协调性，参数α、β和φt应满足如下约束条件：

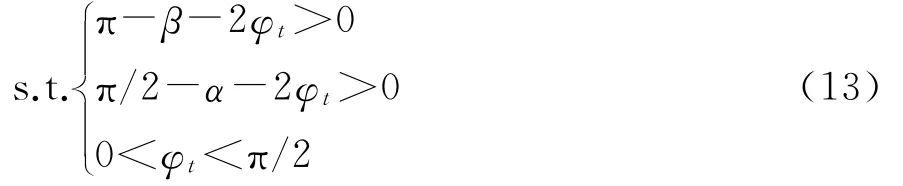
根据极限分析原理，围岩压力上限解可转换成在满足式（13）的约束条件下围岩压力最大值的求解。通过编写优化程序，即可得到特定参数下围岩压力的最优解，还可通过参数分析研究不同参数对矩形浅埋隧道拱顶和边墙围岩压力的影响。

4 算例分析

以某矩形浅埋隧道为工程背景，计算过程中，各参数的取值如下：侧压力系数K=0.8；土体容重γ =20 k N/m3；初始粘聚力c0=10 k Pa；非线性系数m=1.2；埋深H=20 m；跨度h=10 m；地表荷载σs=100 kPa；孔隙水压力系数ru=0.2。通过优化计算，得到隧道拱顶围岩压力q和边墙围岩压力e随各参数的变化趋势如图2所示。

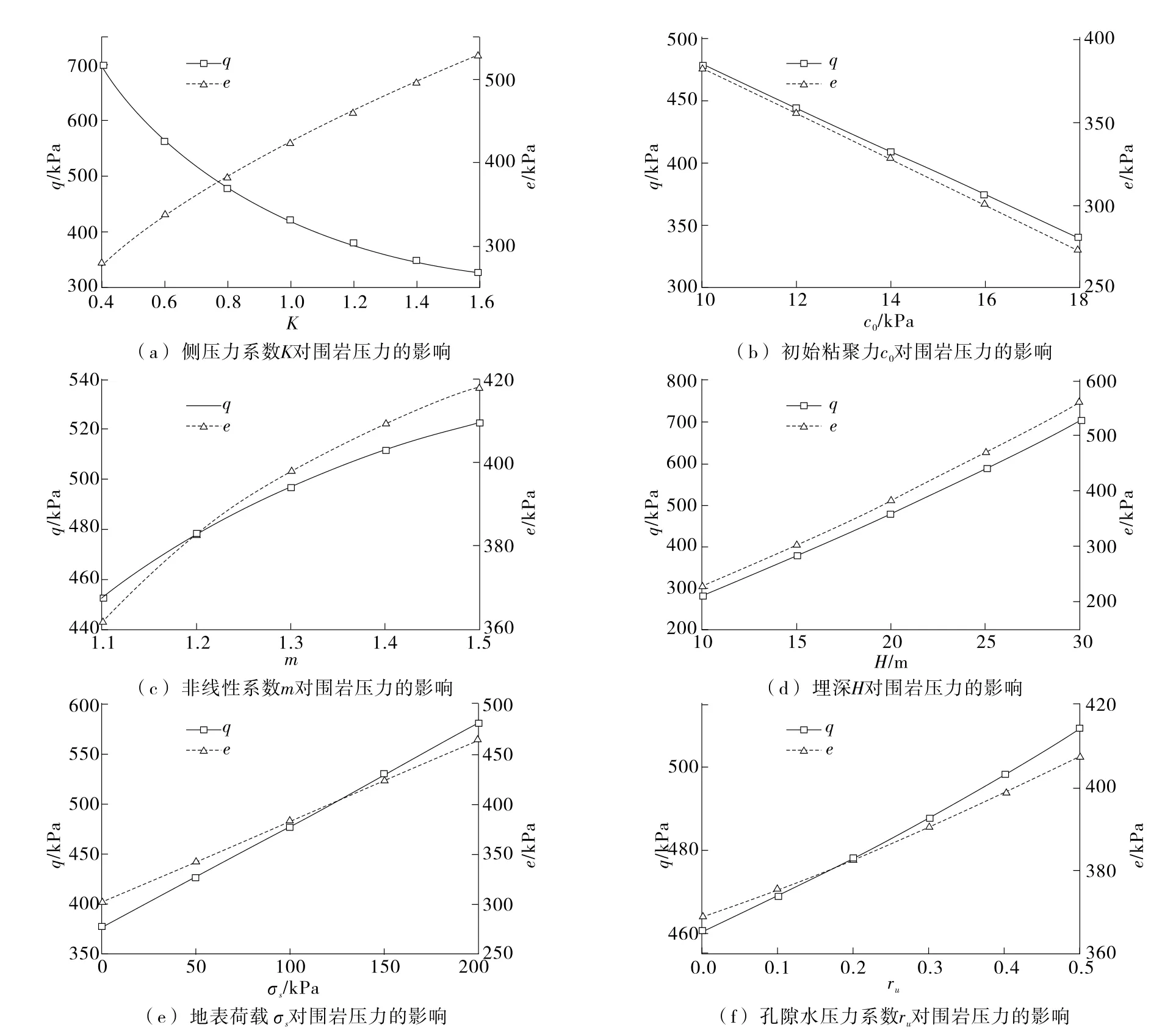
图2　不同参数对围岩压力的影响

从图2可以看出：K取值的不同将导致q和e分布的不同；随着c0的增大，q和e都减小；随着m、H、σs及ru的增大，q和e都增大。岩土体的非线性对围岩压力有较大影响，与线性破坏准则相比，非线性破坏准则能更好地反映土体实际受力情况并得到更为准确的解。此外，围岩压力对K、c0和ru较为敏感。因此，在浅埋隧道设计与施工过程中，应注意根据现场实际情况确定合理的侧压力系数；在初始粘聚力较小的地段施工时，需对拱顶及边墙施加较大的支护力；在富水地层中施工时，应特别注意孔隙水对围岩压力的影响。

5 结论

（1）基于极限分析理论及非线性破坏准则，推导了在包含地表荷载及孔隙水在内的复杂条件下矩形浅埋隧道围岩压力计算公式，并通过数值优化得到了特定参数下的围岩压力上限值。

（2）围岩压力随非线性系数的增大而增大，采用非线性破坏准则进行隧道及地下结构分析可得到更为准确的结果。

（3）地表荷载和孔隙水压力系数的增大都会导致围岩压力增加，建议在浅埋隧道设计与施工过程中注意地表荷载和地下水的影响。

［1］ 谢骏，刘纯贵，于海勇.双平行圆形隧道稳定的塑性极限分析上限解［J］.岩石力学与工程学报，2006，25（9）.

［2］ 杨峰，阳军生.浅埋隧道围岩压力确定的极限分析方法［J］.工程力学，2008，25（7）.

［3］ 赵炼恒，孙秋红，黄阜，等.非关联流动准则对浅埋隧道稳定性影响的上限分析［J］.公路交通科技，2012，29（12）.

［4］ 李玉峰，彭立敏，张永红，等.线性与非线性破坏准则下浅埋隧道围岩压力计算［J］.现代隧道技术，2013，50（5）.

［5］ 伍良波，刘运思.不同埋深比下浅埋隧道稳定性的上限分析［J］.公路工程，2013，38（4）.

［6］ 程小虎.改进的浅埋隧道松动围岩压力计算方法［J］.铁道学报，2014，36（1）.

［7］ 周利金.孔隙水作用下浅埋圆形隧道支护反力上限计算［J］.公路工程，2014，39（4）.

［8］ Drucker D C，Prager W，Greenberg H J.Extended limit design theorems for continuous media［J］.Quarterly of Applied Mathematics，1951（9）.

［9］ Chen W F.Limit analysis andsoil plasticity［M］.New York：Elsevier Scientific Publishing Company，1975.

［10］ Viratjandr C，Michalowski R L.Limit analysis ofsubmergedslopessubjected to water drawdown［J］.Canadian Geotechnical Journal，2006，43（8）.

［11］ Huang F，Yang X L.Upper bound limit analysis of collapseshape for circular tunnelsubjected to pore pressure based on Hoek-Brown failure criterion［J］. Tunnelling and Underground Space Technology，2011，26.

［12］ 杨小礼，王作伟.非线性破坏准则下浅埋隧道围岩压力的极限分析［J］.中南大学学报：自然科学版，2010，41（1）.

［13］ 徐林生.长坪隧道浅埋软弱围岩段施工监测与结构承载状况分析［J］.湖南科技大学学报：自然科学版，2009，24（4）.

［14］ Michalowski R L.Slopestability analysis：a kinematical approach［J］.Geotechnique，1995，45（2）.

U451

A

1671-2668（2016）05-0223-04

2016-07-25