考虑空间相关性及多因素影响的初锈时间模型与失效概率分析

阳海斌

（育才-布朗交通咨询监理有限公司，湖南长沙 410076）

考虑空间相关性及多因素影响的初锈时间模型与失效概率分析

阳海斌

（育才-布朗交通咨询监理有限公司，湖南长沙 410076）

为了研究多因素影响下氯离子扩散规律及结构失效概率，基于Fick第二扩散定律，综合考虑水灰比、温度、湿度、预应力等多参数影响及氯离子扩散系数时变性，在考虑材料性能和尺寸参数空间相关性的基础上得到钢筋初锈时间，对钢筋初锈时间的影响因素进行了敏感性分析，发现适当增加砼保护层厚度及临界氯离子浓度能明显延缓钢筋的初始锈蚀，而表面氯离子浓度的增加对钢筋锈蚀起促进作用，与不考虑空间相关性结果相同；利用极限状态函数建立结构可靠度计算功能函数，得到了考虑空间相关性后的失效概率计算模型。

桥梁；时变；氯离子扩散；钢筋初锈时间；Mote-Carlo模拟；失效概率

大量研究表明，钢筋砼结构耐久性降低或失效主要是由于氯离子侵蚀导致的钢筋锈蚀引起的。氯离子侵入砼内部主要包括渗透、扩散、电化学作用等方式，目前主要基于Fick第二扩散定律研究砼中氯离子的扩散并对其扩散模型进行修正。余发红等在考虑氯离子扩散系数后对扩散方程进行了修正；滕海文等综合考虑环境因素及砼材料特性，与边界条件相结合，得到了改进的氯离子扩散模型；王仁超等研究了温度、砼结合效应等参数的影响，建立了新的氯离子扩散模型。但上述研究并未综合考虑水灰比、温度、湿度、预应力等因素及各材料参数、结构尺寸的空间相关性的影响，有必要对氯离子扩散时变模型进一步开展研究。

目前不少学者对结构的可靠度及失效概率进行了分析：马亚丽等以Fick第二扩散定律为基础，在未考虑氯离子扩散系数时变性下得到了氯盐环境下RC结构耐久性预测模型，但忽略了氯离子扩散随时间的变化规律；施惠生等考虑氯离子结合效应及氯离子扩散时变性等因素的影响，对处于海洋环境下的砼结构的耐久性进行了预测，但未考虑其他因素对氯离子扩散的影响。

该文以Fick第二扩散定律为基础，综合考虑氯离子扩散系数时变性及水灰比、温度、湿度、预应力等参数的影响，对氯离子扩散时变模型进行研究，并利用极限状态函数建立结构可靠度计算功能函数，得到失效概率计算模型。

1 氯盐环境下结构初锈时变模型

1.1初始模型

氯离子侵蚀是导致钢筋砼构件承载力显著降低的主要原因，以往研究表明，氯离子在砼中为线性扩散，与Fick第二扩散定律相似，其规律可表示为：

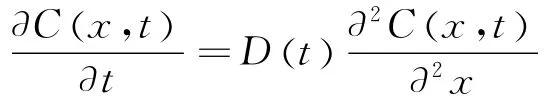
式中：C（r，t）表示在时间t（年）时距砼表面r（cm）处的氯离子浓度（%）；D（t）为氯离子扩散系数，与时间t有关。

1.2多因素对氯离子时变扩散系数的影响

（1）水灰比的影响。砼结构内部孔隙结构很大程度上受砼水灰比（w/c）的影响，而孔隙率的大小影响氯离子在砼中的传播。水灰比越大，砼内部的孔隙率越大，氯离子扩散速率越大。目前一般以28 d标准养护下得到的氯离子扩散系数为基础进行研究，其表达式为：

（2）温度的影响。氯离子扩散速率随着温度的升高而增大。文献［8］给出了温度效应对氯离子扩散系数的影响公式：

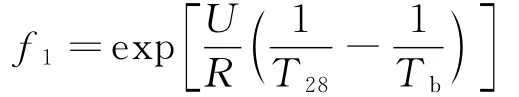
式中：f1为温度修正系数；U为激活能量，取35 000 J/mol；R为气体常数，R=8.314 J/（mol·K）；T28为标准养护28 d时的绝对温度，一般取293 K；Tb为所需计算时刻的温度。

（3）湿度的影响。水是砼中氯离子发生扩散的必要因素之一，对氯离子扩散速率存在不小的影响，因此，计算中必须考虑湿度对氯离子扩散速率的影响。其表达式为：

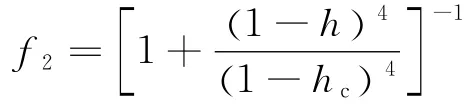
式中：h为湿度，大气区取75%，浪溅区取90%，潮差区取95%；hc为临界相对湿度，一般取75%。

（4）预应力的影响。氯离子扩散系数在无应力状态和应力状态下存在明显差异。这里主要通过压应力水平（应力值与抗压强度的比值）来考虑砼结构受压状态对氯离子扩散的影响。其关系式为：

经访问得知,这些样本人群中除部分通过专八考试的学生外，极少的同学对自己的思辨性翻译能力有信心。除了个别主观因素之外，根据调查显示，传统英语教学的测试环节中，无论是选拔性的高考，研究生考试，还是水平性的各类证书考试(CET4，6级，TEM4，8级)，都在一定程度上扼杀了学生思考问题，提出问题，分析问题的能力。评价学生能力的尺度也仅仅是考试的分数，这从一开始就进入了一个死板的记忆与应试的循环中，使得常规的翻译教学对学生的评价比较单一，即关注最终译文的优劣而忽视翻译过程中的动态评估。

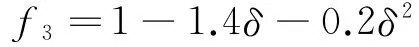
式中：δ为压应力水平，其值可根据28 d抗压强度实测值选取，为压应力与28 d抗压强度之比。

根据以上分析，氯离子时变扩散系数与水灰比、温度、湿度和应力水平有关，关系如下：

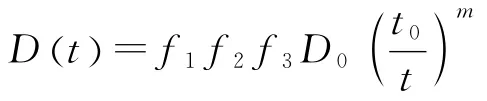
式中：m为扩散衰减系数，m=（0.8-w/c）+0.4×（FA/50+SA/70）；w/c为水灰比；FA为粉煤灰所占水泥总量的百分比，FA≤50%；SA为矿渣所占水泥总量的百分比，SA≤70%。

1.3多因素影响的氯离子时变扩散模型

文献［12］研究表明：砼表面氯离子浓度与扩散规律存在差异，可用稳定扩散区界面的氯离子浓度表示。具体关系如下：

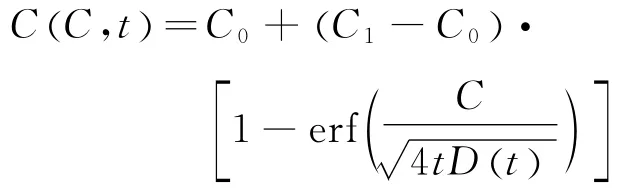
式中：C0为钢筋砼构件中初始氯离子浓度（%）；C1为稳定扩散区界面氯离子浓度（%）；erf为误差函数；C为保护层厚度（mm）；t为时间（年）。

考虑水灰比、温度、湿度、预应力等多因素的影响，钢筋砼构件的初始锈蚀时间T1可由下式计算：

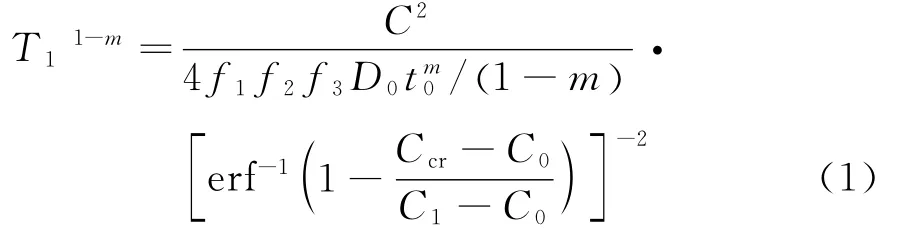
式中：erf-1为误差函数反函数；Ccr为砼表面氯离子临界浓度（%）。

2 参数的空间相关性分析

由于施工工艺的影响，结构尺寸和材料性能在构件不同位置存在差异，对结构的耐久性影响较大。考虑保护层厚度C、表面氯离子浓度Cs、临界氯离子浓度Ccr的空间相关性，采取划分单元的方法，将钢筋砼结构底板划分为N个正方形单元，每个小单元尺寸为Δ。同时只要单元划分完成，则描述各参数的相关性矩阵也随之确定。采用下式描述相关单元的相关性：

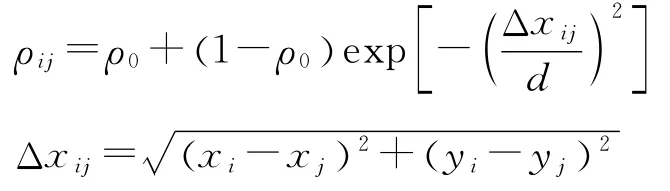
式中：i、j为相关单元编号；ρ0为相关系数，取0.5；d为波动系数，取2。

对应的相关系数矩阵为：

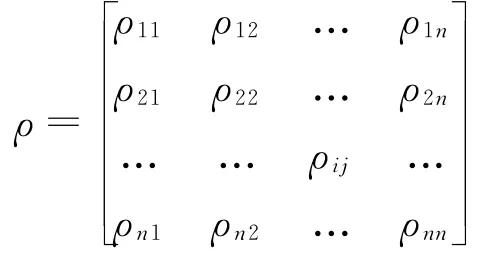
式中：ρij表示第i个单元和第j个单元的相关系数。

3 考虑空间相关性时初锈时间模型参数敏感性分析

根据式（1），考虑空间相关性时，保护层厚度、氯离子扩散系数、氯离子临界浓度及表面氯离子浓度、温度、湿度等均对结构的初锈时间存在不同影响，且上述参数的统计特性对初锈时间的分布有较大影响。因此，需对考虑空间相关性时的初锈时间模型参数进行敏感性分析。

以一砼结构底板（长10 m，宽2.5 m）为研究对象，以0.5 m为单元尺寸划分底板单元，共得到100个离散单元。利用文献［14］中给出的影响结构初锈时间的参数统计特征（见表1），采用Mote-Carlo方法对式（1）进行模拟，得到结构初锈时间的概率密度函数（见图1）。从中可见，在各因素共同影响下，钢筋初锈时间的分布近似于对数正态分布，考虑空间相关性时，初锈时间在8.62年时发生概率最大，比不考虑空间相关性时提前17.91%。考虑空间相关性可为桥梁的维修加固时机提供依据。

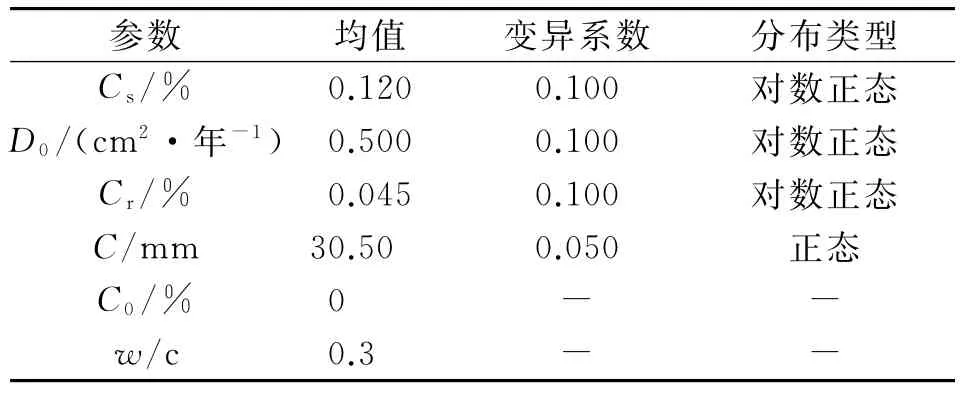
表1　初锈时间影响参数统计特征

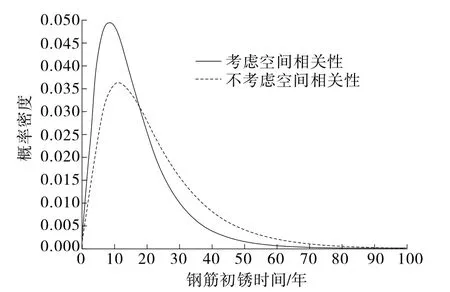
图1　初锈时间概率密度函数

采用相同的方法得到不同保护层厚度C、表面氯离子浓度Cs、临界氯离子浓度Ccr对初锈时间的影响曲线（见图2～4）。

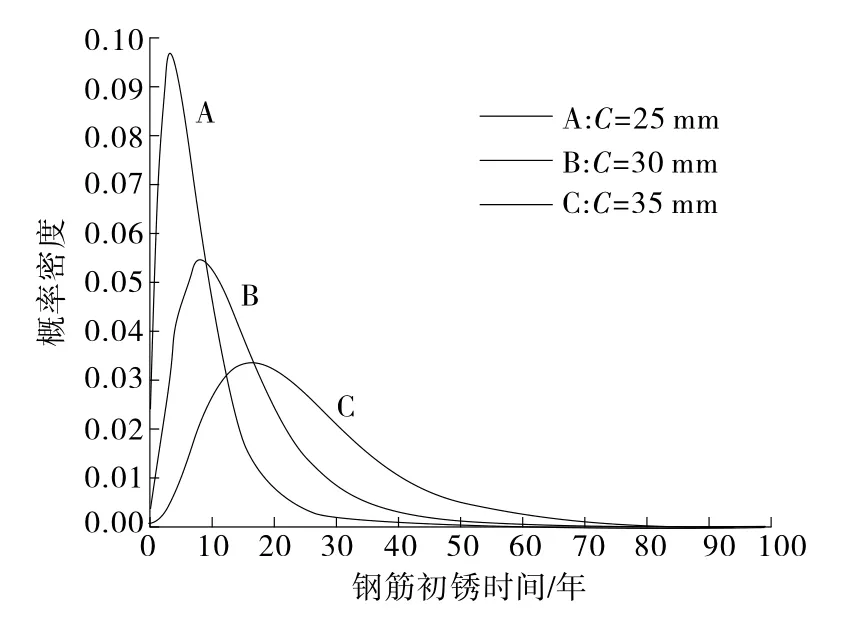
图2　保护层厚度C对初锈时间概率分布的影响

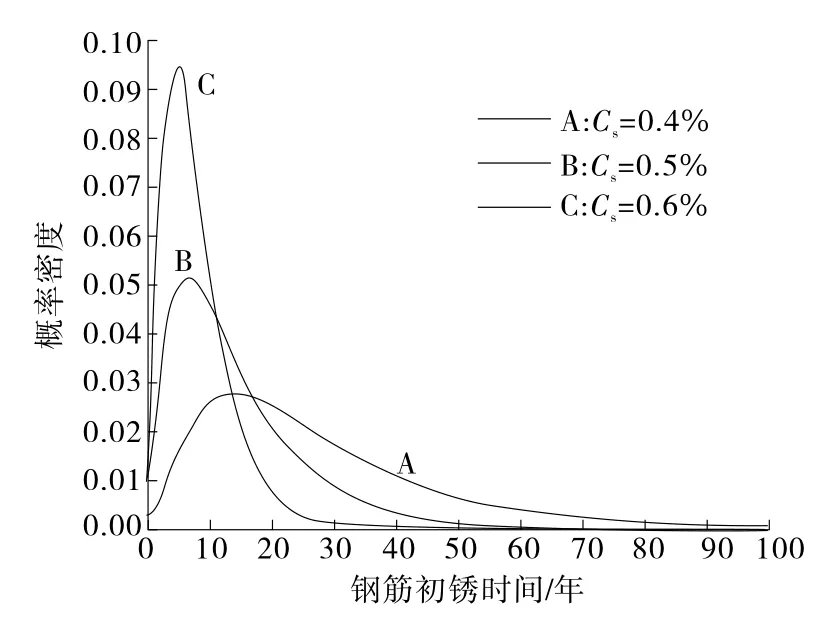
图3　表面氯离子浓度Cs对初锈时间概率分布的影响

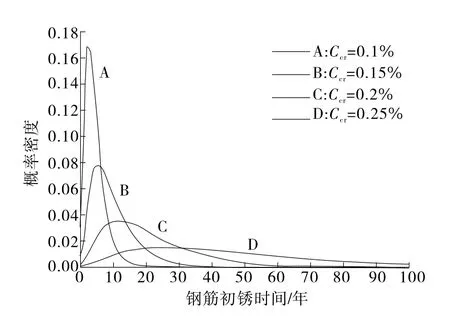
图4　临界氯离子浓度Ccr对初锈时间概率分布的影响

由图2可以看出：当保护层厚度从25mm增加到35mm时，钢筋初锈时间均值由6.74年增加到16.92年；同时根据式（1），初锈时间Ti与保护层厚度C的平方呈正相关。说明适当增加砼保护层厚度能明显延缓钢筋的初始锈蚀，这对保护结构的耐久性和安全性十分重要。

由图3可知：当表面氯离子浓度由0.4%增加到0.5%时，初锈时间Ti大约为原来的一半，初始锈蚀明显加快；当表面氯离子浓度由0.5%增加到0.6%时，初锈时间Ti略微下降，变化不明显。这是由于表面氯离子浓度较小时，加大表面氯离子浓度能提高氯离子的扩散速度，从而加快钢筋锈蚀；但表面氯离子浓度增大到一定程度后，其加速钢筋锈蚀的作用不再明显。

由图4可知：当临界氯离子浓度由0.1%增加到0.25%时，钢筋去钝化时间增大，钢筋初锈时间明显延长，且增长速度由小变大，从而对钢筋及结构起到保护作用。

综上所述，无论是否考虑空间相关性，保护层厚度C、表面氯离子浓度Cs、临界氯离子浓度Ccr对初锈时间的影响规律不变。

4 失效概率分析

在利用极限状态函数进行可靠度计算时，目前一般是将钢筋开始发生锈蚀与钢筋表面氯离子浓度达到临界氯离子浓度进行等价处理。耐久性可靠度可定义为时间t时钢筋临界氯离子浓度与表面氯离子浓度之差，表达式如下：

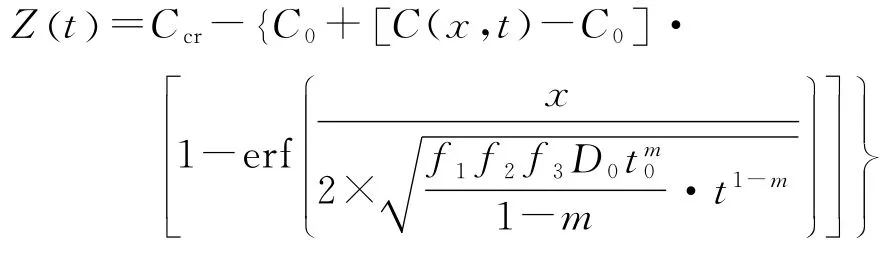
考虑空间相关性时，氯离子环境下结构发生腐蚀的概率为：

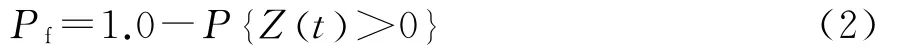
基于MATLAB软件对各影响参数的随机抽样，对式（2）进行Mote-Carlo模拟，得到结构服役时间（0～100年）与结构失效概率的关系（见图5）。

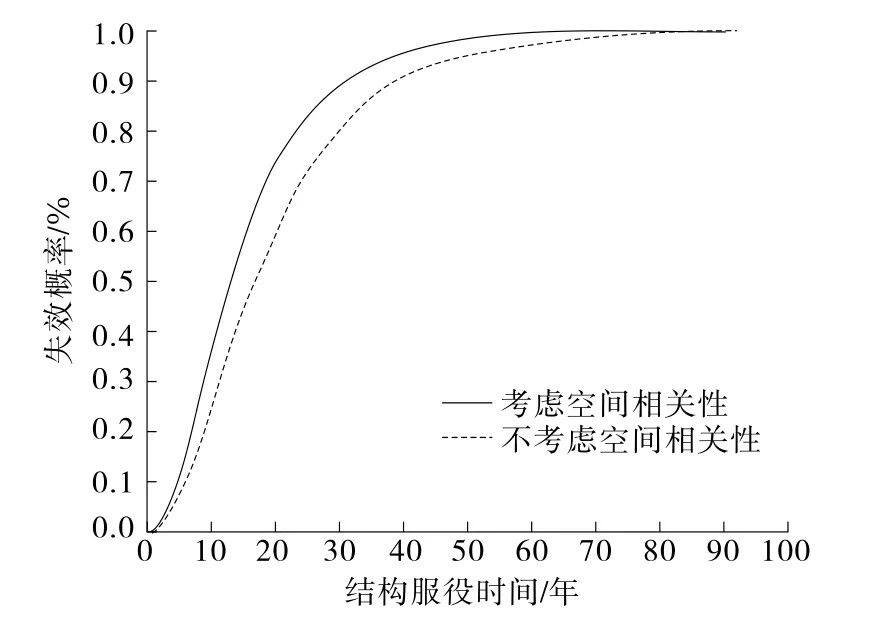
图5　结构服役时间与失效概率

由图5可知：考虑空间相关性时，结构失效概率比不考虑空间相关性时大幅提高，如在结构服役30年时，考虑空间相关性和不考虑空间相关性时结构失效概率分别为0.885%和0.802%，前者比后者提高10.35%。可见，不考虑空间相关性将高估结构的耐久性。

5 结论

该文基于Fick第二扩散定律，考虑氯离子扩散系数时变性、多因素影响下氯离子扩散时变模型和材料性能及结构尺寸的空间相关性，得到了钢筋初锈时间；基于Mote-Carlo模拟，得到了钢筋初锈时间的概率密度函数，同时在考虑空间相关性时对影响初锈时间的各因素进行敏感性分析，发现适当增加砼保护层厚度及临界氯离子浓度能明显延缓钢筋的初始锈蚀，而表面氯离子浓度的增加对钢筋锈蚀

起促进作用，与不考虑空间相关性时的规律一致；利用极限状态函数建立结构可靠度计算功能函数，得到失效概率计算模型，并基于MATLAB对各影响参数的模拟，得到了结构服役时间与结构失效概率关系曲线，发现不考虑空间相关性将高估结构的耐久性。

［1］ 夏晓慧，刘小平，聂美春.腐蚀钢筋混凝土构件斜截面承载能力分析［J］.公路工程，2012，37（5）.

［2］ 杨和平.浅谈钢筋保护层厚度对桥梁结构的影响［J］.公路工程，2011，36（6）.

［3］ 余红发，孙伟，麻海燕，等.盐湖地区钢筋混凝土结构使用寿命的预测模型及其应用［J］.东南大学学报：自然科学版，2002，32（4）.

［4］ 滕海文，舒正昌，黄颖，等.多因素作用下钢筋混凝土构件氯离子扩散系数模型［J］.土木建筑与环境工程，2011，33（1）.

［5］ 王仁超，朱琳，杨弢，等.综合机制下氯离子扩散迁移模型及敏感性研究［J］.海洋学，2006，30（7）.

［6］ 马亚丽，张爱林.基于规定可靠指标的混凝土结构氯离子侵蚀耐久寿命预测［J］.土木工程学报，2006，39（2）.

［7］ 施惠生，王琼.海工混凝土使用寿命预测研究［J］.建筑材料学报，2004，7（2）.

［8］ 陈强，彭建新.氯盐环境下考虑温湿度影响的钢筋混凝土梁桥二维扩散模型及可靠度分析［J］.铁道科学与工程学报，2014，11（2）.

［9］ Saetta Anna V，Scotta Roberto V.Analysis of chloride diffusion into partiallysaturated concrete［J］.ACI Material Journal，1993（5）.

［10］ 张伟平，张庆章，顾祥林，等.环境条件和应力水平对混凝土中氯离子传输的影响［J］.江苏大学学报：自然科学版，2013，34（1）.

［11］ 李丽，吴相豪.海工混凝土结构钢筋表面去钝化时间的预估方法［J］.南昌工程学院学报，2006，25（1）.

［12］ 杨绿峰，胡春燕，陈正，等.混凝土中氯离子随机时变扩散过程及浓度分布［J］.建筑材料学报，2013，16（2）.

［13］ Ying Li，Ton Vrouwenvelder，Geert Henk Wijnants. Spatial variability of concrete degradation［A］.Life-Cycle Performance of Deteriorating Structures［C］. 2003.

［14］ Ma Yafei，Zhang Jianren，Wang Lei，et al.Probabilistic prediction with Bayesian updating forstrength degradation of RC bridge beams［J］.Structural Safety，2013，44.

［15］ 周峰，王银辉，李应根.钢筋砼耐久性下降原因及提升方法［J］.公路与汽运，2016（4）.

［16］ 马亚丽，张爱林.混凝土结构钢筋初锈时间的概率模型［J］.水利学报，2007，38（5）.

［17］ 刘鹏.氯盐环境下钢筋蚀坑深度时变模型［J］.山西建筑，2015，41（26）.

［18］ 刘欣.荷载氯盐侵蚀耦合作用下混凝土构件寿命预测研究［D］.天津：天津大学，2012.

［19］ 王华.RC桥梁混凝土中氯离子扩散试验研究及概率分析［D］.长沙：长沙理工大学，2013.

U443.35

A

1671-2668（2016）05-0159-04

2016-03-30