城市自助式公共出租车的调度问题探讨*

高志波，吴立烜，彭巍，王倩

（1.长沙理工大学交通运输工程学院，湖南长沙 410004；2.中国民航大学空中交通管理学院，天津 300300）

城市自助式公共出租车的调度问题探讨*

高志波1，吴立烜1，彭巍1，王倩2

（1.长沙理工大学交通运输工程学院，湖南长沙 410004；2.中国民航大学空中交通管理学院，天津 300300）

自助式公共出租车是一种缓解城市交通问题且适合城市内部短时双向出行的交通方式，既能减少私家车的使用率，又能满足顾客的个性化需求。城市交通流的潮汐现象导致各网点供需不均衡，极大影响整个系统的运行。针对该缺陷，文中根据不同时刻各网点的车辆数和顾客的需求量，综合考虑运输顾客、空车调配、原地停留等情况的效益，引入惩罚因子对模型进行改善，得到总费用最小、满意度最佳的决策方案；根据问题特征，设计了求解该问题的简单函数逼近算法，给出了具体求解流程；最后结合算例，计算得到了最佳城市自助式公共出租车调度方案。

城市交通；自助式出租车；空车调度；函数逼近

自助式公共出租车是基于“汽车共享”理念的一种新的出租车运营服务，比传统汽车租赁的时长更短，比出租车出行更个性化和方便，能替代私家车出行。如何科学、有效地调配空车、控制和降低车辆调配成本已成为影响城市自助式出租车公司运作的关键因素之一。

Matthew Barthand等通过建立多网点汽车共享服务仿真模型，详细评估了汽车共享服务车辆的分配及使用情况；Karbassi A.等提出了一种汽车共享中路线预测和到达时间评估方法，可在多站台车辆系统中实现，开发的算法能测算出实际运送路径和到达时间；黄肇义在分析汽车共享产生意义的基础上，提出了国内推广汽车共享服务的具体措施；周长峰等提出了两种时间窗类型的动态车队问题，分别以任务分配策略和任务类型的不同构造相应目标函数，分析了针对局部问题的混合整数规划模型，给出了求解的实际操作策略；且丽莎从汽车共享服务公司和用户等多个角度考虑，分别建立了随机需求与考虑用户满意度的汽车共享空车调配模型。但在实际情况下，需求情况往往是不能全部预知的，不能简单地处理为一个确定性的规划问题。为此，该文以城市自助式公共出租车整体费用为目标，建立需求不完全满足的确定性空车调配模型，并针对该模型特点及整数解等要求，通过空间和时间上的分解将空车调配问题简化为若干前后关联的时空阶段进行求解。

1 问题描述

在自助式公共出租车的运营过程中会出现供给与需求不均衡的情况，分为应急、偶发的情况和常规、定期的情况，需采取车辆诱导与空车调度等方式来满足用户的用车需求。

（1）应急情况下车辆诱导。调度信息中心对用户用车的目的地进行实时反馈，当监控中心监测到路面行驶的车辆出现“潮汐”现象时，将引导指令反馈给区域内的车辆用户，建议就近网点停车，实现分散和引流的目的。

（2）常规空车调度。空车调配情况是紧急状况下为保证网点高效运营而作出的被动措施，一般分为两种情况：一是各网点库存车辆与任务所需车辆数不平衡，即车辆供不应求；二是网点间在某时段车辆的供需情况不协调，即可能存在有些网点车辆过剩，使得网点停车位不够还车停放的现象。

2 车辆调度决策模型

2.1条件假设

（1）交通条件。假定网点与网点之间的运输网络结构稳定，各网点的任务需求、车辆数量及车辆状态随时段的推进而变化。

（2）服务周期。设定的整体服务时间范围能按一定时长分成若干时段，各时段内每个网点均能产生运输任务。

（3）网点间运输时间。由于设定运输网络稳定，各网点之间的车辆运行时间确定。

（4）车辆分布状态。车型相同，任意时刻一辆车可服务所有类型任务，但仅服务一个任务需求。

（5）提前决策。每个时段初可配置好本时段所需的车辆和车位。

（6）初始状态。服务周期初始时各网点处的车辆分布情况可从控制中心得知。

（7）车辆使用形式。车辆在网络系统中循环使用。

（8）忽略固定成本。不考虑员工薪酬成本、车辆负荷、员工负荷等情况。

2.2目标函数

根据上述分析，建立如下目标函数：

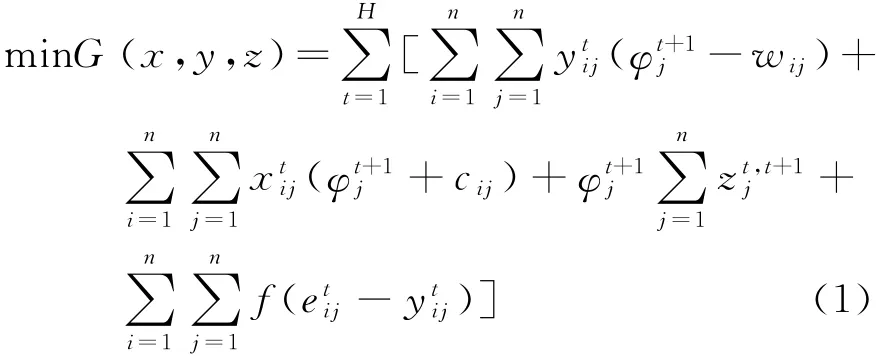
式中：t为服务周期，以Δt等分为H个时段，从而服务周期可表示为t=｛1，2，...，H｝；H为大于等于1的正整数；n为网点个数；ytij为时段t从网点i到j分配空车服务的任务数，∀i≠j；φtj+1为j网点在t+1时刻增加一辆车的边际费用函数；wij为发送运输任务从网点i到网点j所能创造的纯利润；rtij为从网点i到网点j的空车移动数，∀i≠j；cij为网点i与j间空车移动的成本；zti，t+1为网点i由t时段原地停留到t+1时段的空车数；etij为有载客需求从网点i到网点j并且在t时段起运的任务数。

式（1）中，第一项为车辆选择运输客户的费用，第二项为车辆选择空车调配产生的费用，第三项为车辆原地停留的费用，第四项为不能满足顾客需求产生的惩罚费用。

2.3约束条件

（1）数量约束：

（2）服务任务数约束：

（3）停车位约束：

（4）还车约束：

（5）空移车数、原地驻留车数总和的上限约束：

3 算法设计思路及流程

3.1目标函数的简化与分析

利用函数逼近的方法简化目标费用函数的表达，运用线性费用函数近似替代目标函数中的Gt+1（St+1，Pt+1）（见图1），从而将原问题分解为复杂的多阶段、多网点问题。

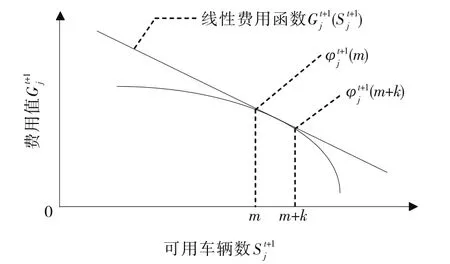
图1　费用函数的线性逼近

用图1所示的直线逼近该费用曲线时，当费用函数被线性函数替代后，斜率不变，边际费用可近似用斜率表示，即边际费用成为常量，与无关，从而无需确定时段t其他各网点发往j网点的车辆数。

3.2边际费用确定及更新

每辆车可选择载客服务、空车移动和原地停留3种运作方式。对于车辆的不同选择方式，费用值λtNi各不相同：1）当t时段车辆选择载客移动时，当t时段车辆选择空车移动时当t时段车辆选择原地停留时

由于控制变量φt（m）的更新需通过不断调整以达到最优，设第m次调整后的状态向量为（St（m），Pt（m））、解向量为（rt（m），yt（m），zt（m）），选择指数平滑法确定和更新控制变量φt（m），过程如下：

式中：φm为第m次调整的平滑指数；φ为根据经验选择的数值；αt（m+1）i表示第m+1次调整中总费用函数关于的导数。

3.3空移车辆数上限确定及更新

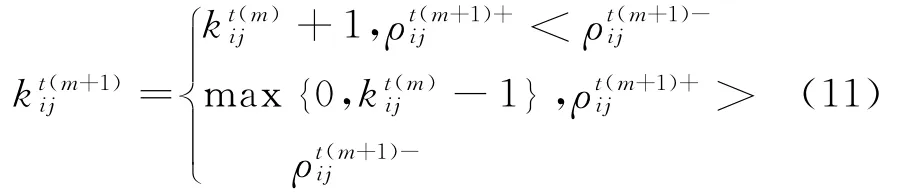
3.4算法设计

基于上述分析，算法的核心步骤是如何求解各独立的单时段单网点车辆调配问题；辅助步骤是确定边际费用控制变量及其更新过程，该步骤的实质是进行多次调整，即和每更新一次，就对核心步骤的调配过程进行调整，逐次更新调整直至达到最优解。算法流程见图2。

图2　算法流程

4 实例分析

根据已知网点的布局方案，设立12个自助式公共出租车网点，记为n=｛1，2，…，12｝；系统共有317辆车、360个停车位。假设任意两个网点间的行驶时间都为1，服务周期内共分为3个任务产生时段，记为t=｛1，2，3｝；网点间的空车调度成本（见表1）、租赁的费用（见表2）、初始的网点分布情况（见表3）、各时段各网点产生的任务（见表4～6）均为已知。下面运用上述模型求解每个时段各网点的空车调配情况。

表1　网点间空车调度及空闲的成本　元

续表1

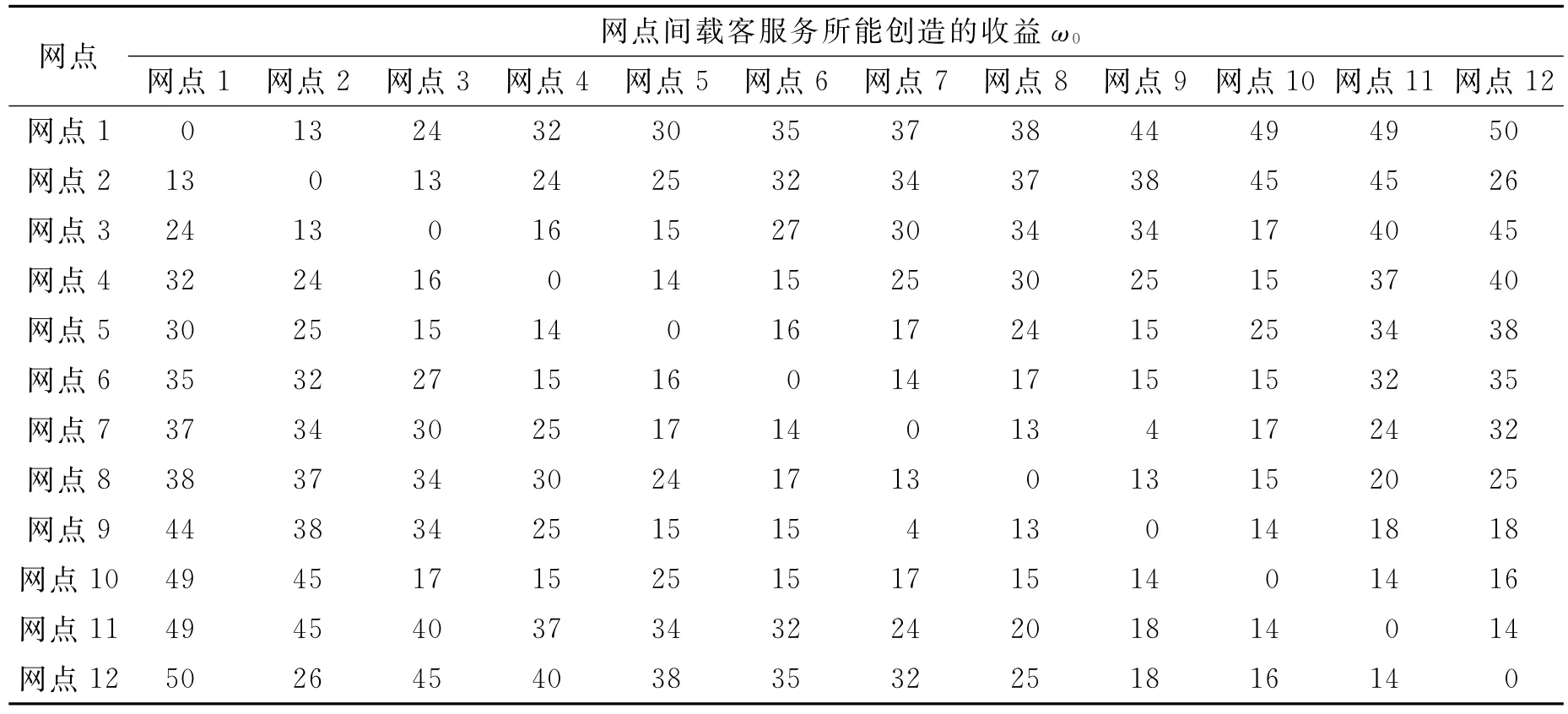
表2　网点间载客服务所能创造的收益　元

表3　各网点初始车辆分布情况

表4　时段1各网点的任务情况　辆

表5　时段2各网点的任务情况　辆

表6　时段3各网点的任务情况　辆

运用MATLAB对上述算法与数据进行计算，得出每个时段空车调度方案（见表7～9）。

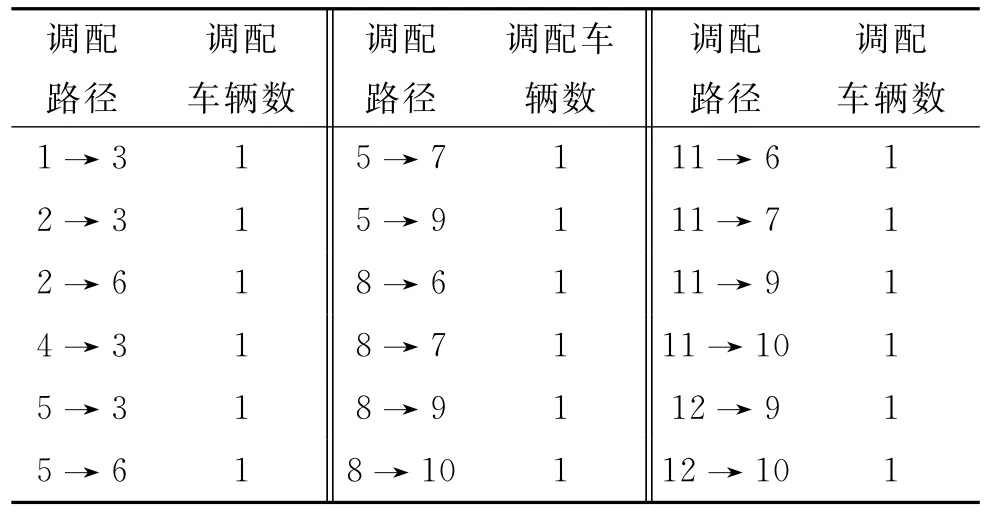
表7　时段1空车调配方案　辆

表8　时段2空车调配方案　辆

表9　时段3空车调配方案　辆

5 结语

该文以公共出租车整体费用为目标，建立了需求不完全满足的确定性空车调配模型。针对模型特点及整数解等要求，通过空间和时间上的分解将空车调配问题简化为若干前后关联的时空阶段，利用函数逼近思想，引入线性的边际费用函数近似代替原目标函数来求解模型。

但在模型假设时给出的车辆在运输网络系统中任意网点间的运行时间相等，这在实际中很难实现，需将车辆运行时间引入该多时段动态空车调配问题中作进一步研究。

［1］ Matthew Barthand，Michael Todd.Simulation model performance analysis of a multiplestationshared vehiclesystem［J］.Transportation Research，1999（7）.

［2］ Karbassi A，Barth M.Vehicle route prediction and time of arrival estimation techniques for improved transportationsystem management［A］.Intelligent Vehicles Symposium［C］.2003.

［3］ 黄肇义.国内城市交通发展“汽车共用”的探讨［J］.城市交通，2004（3）.

［4］ 周长峰，廖良才，谭跃进.多任务类型的动态车队管理问题求解方法研究［J］.中国企业运筹学，2007（6）.

［5］ 且丽莎.基于“汽车共享”的空车调配问题研究［D］.成都：西南交通大学，2010.

［6］ 徐志良，张凤鸣.出租汽车连续配车的一个优化逼近探索模型［J］.上海机械学院学报，1983（4）.

U492.2

A

1671-2668（2016）05-0033-05

2015年湖南省普通高等学校教学改革研究立项项目资助（JW-0823）

2016-03-15