基于GPS车速数据驱动模型的高速公路极限匝道间距识别

汪 帆，李 岩,，刘建蓓，李 元，夏立品

(1.长安大学 公路学院，陕西 西安 710064;2.中交第一公路勘察设计研究院有限公司，陕西 西安 710075)



基于GPS车速数据驱动模型的高速公路极限匝道间距识别

汪 帆1，李 岩1,2，刘建蓓2，李 元1，夏立品1

(1.长安大学 公路学院，陕西 西安 710064;2.中交第一公路勘察设计研究院有限公司，陕西 西安 710075)

建立了基于GPS车速的数据驱动模型及间隙接受模型，以识别高速公路在极限状态下可采用的最小匝道间距。将高速公路匝道间距划分为加速影响区、减速影响区和交织换道区;建立GPS车速数据驱动模型识别车辆汇入后的加速影响范围和车辆驶出前的减速影响范围;根据可接受间隙理论建立极限管控条件下的交织换道区影响范围的识别模型；应用某市出租车在测试路段指定时段内的GPS时空车速数据分析。结果表明，加减速影响区的范围与车速线性相关。提出将多车道高速公路的直行车流与合、分流车流相分离，基于可接受间隙的模型测算结果表明交织换道区的距离不应小于639 m。在分流主线通过型交通流，交织换道区限速80 km/h，设置辅助车道时，二级服务水平下的极限匝道间距为872 m，考虑安全性，推荐设置为930 m以上。

交通工程; 多车道高速公路极限匝道间距; 数据驱动模型; 间隙接受理论; GPS浮动车数据; 高速公路管控

0 引言

高密度高速路网的建设会造成互通立交间距需突破规范最小值的情况，受限于用地及道路设计要求，互通立交间距甚至会需突破极限间距，此时需通过必要的交通管控措施保障交通流运行的效率及安全[1-2]。当互通立交间距突破极限间距时，从上游匝道汇入高速公路主线的车辆会对从下游匝道驶出的车辆产生影响，部分车辆甚至会难以自由完成换道，给高速公路安全运行带来极大隐患[3-4]。因此在突破互通立交极限间距时，需在明确交通流运行特性的基础上，降低车辆加、减速和换道等行为的影响[5]。海量全天候的GPS运行数据为分析各类高速公路车辆运行特性奠定了基础[6-7]。通过建立GPS车速数据驱动模型，识别具备高密度交叉路网特性的小间距互通立交间的车辆运行特性，可为分析极端状况的交通运行特性，识别高速公路互通立交的极限间距奠定基础。

互通立交间距指相邻互通立交高速公路主线的间距，即两条相交道路和主线交叉点间的距离[8]。在对比各互通立交间距下交通流运行特性时，常因互通立交的形式、组合及加减速车道、匝道等的设置不同而无法直接类比[9]。因此，在评价互通立交间距时，宜选用作为系统通行能力的“瓶颈”区及交通事故多发处的匝道间距[10]进行评价。匝道间距为两个相邻匝道与主线合流或分流处三角形鼻端间的距离[8]，其在美国2010版的《道路通行能力手册》(HCM2010)中也被作为交织区长度计量标准[11]。互通立交间距和匝道间距的对比如图1所示。应用匝道间距作为评价对象，可消除互通立交设置及组合形式的影响，从而直观反映小间距立交高速公路的交通运行状况[12-13]。

国内外关于互通立交或匝道间距设计的相关规范主要有：美国国家公路与运输协会(American Association of State Highway and Transportation Officials, AASHTO)的《APolicyonGeometricDesignofHighwaysandStreets》(一般称为绿皮书)[14]、国内的《公路通行能力手册》、《公路路线设计规范》(JTG D20—2006)等。但上述规范均未将速度作为确定互通立交间距的确定因素，而美国的《道路通行能力手册》显示匝道间距会对速度产生影响[11]，旧的AASHTO规范也指出推荐匝道间距与车速相关[15-16]，即可根据路段运行车速特征计算合理最小匝道间距[17]。应用实测数据回归技术[18]、数据包络分析[19]、交通冲突技术[20-21]、动力学与可接受间隙技术[22]等方法均证明车速与匝道间距相关。因此，根据GPS车速数据可识别匝道的极限间距。论文在划分匝道间运行特征区域的基础上，建立了由GPS车速数据驱动模型及可接受间隙模型的各功能区极限间距识别模型，并讨论各管控措施下高速公路互通立交设置突破匝道极限间距时的建议。

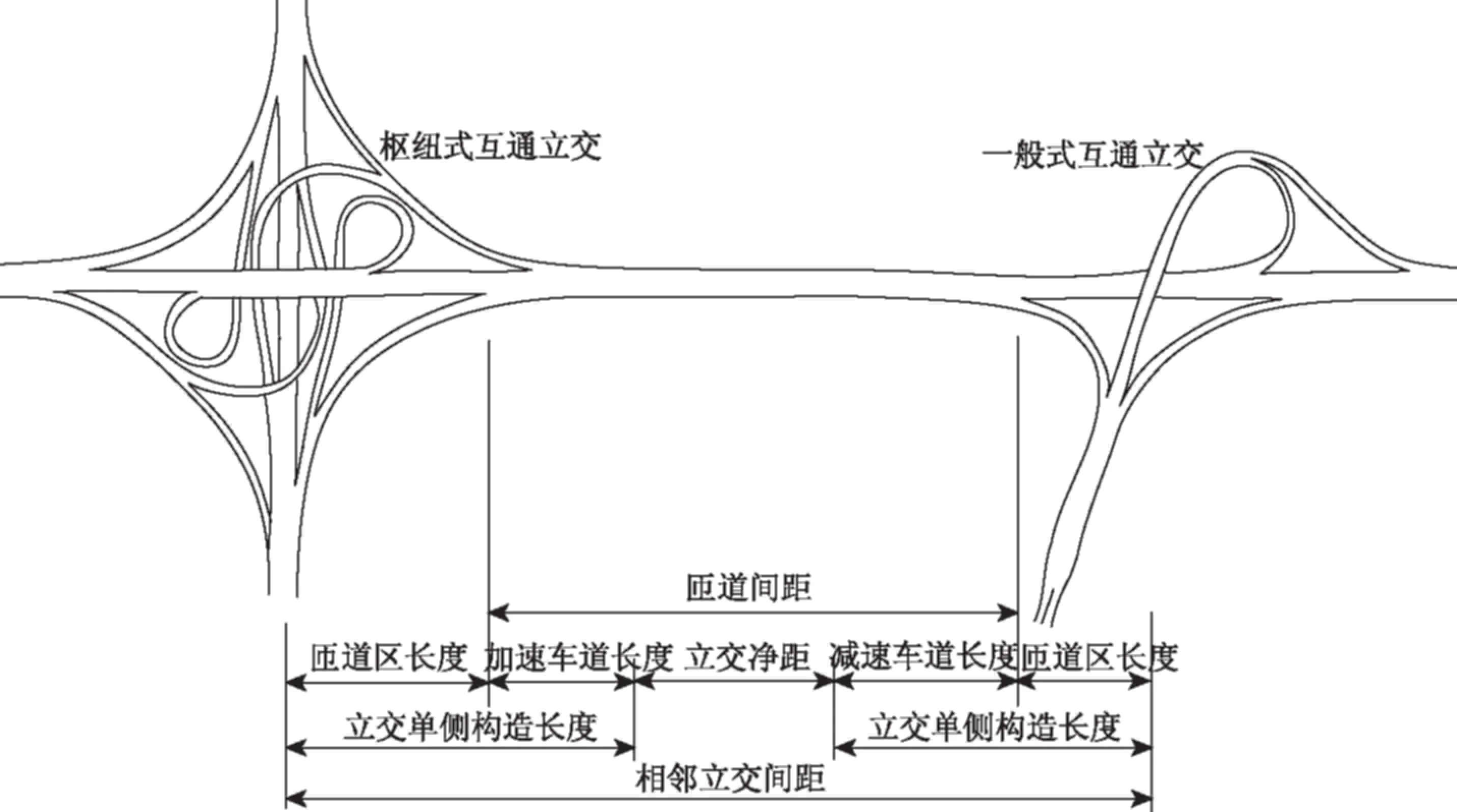
图1 高速公路互通间距与匝道间距的对比Fig.1 Comparison between interchange spacing and ramp spacing of expressway

1 高速公路互通匝道间距识别模型

1.1 高速公路匝道间距的组成及特性

高速公路的互通立交可分为枢纽式互通立交及一般式互通立交。因高速公路主线上相邻两互通立交间的路段封闭，其匝道与主线交叉的组合形式均应为入口-出口型。在设置互通立交匝道间距时，应满足从上游匝道汇入的车流与从下游匝道驶出的车流安全、非交织运行要求，同时应满足下游互通立交设置预告标志所需的前置距离要求[22]。如图2所示，匝道间的车辆可分为通过型车辆(如车辆MnM)、合流车辆(车辆R1M)及分流车辆(车辆MnR)。车辆编号说明：第一个字母为车辆原始位置，最后一个字母为车辆前进目标，中间一个字母为车辆应换道数。M指主线，R指匝道，n和1均指换道数。按各类车流在匝道间运行的特性，可将匝道间距划分为车辆加速影响区、交织换道区及车辆减速影响区。与基于道路设计元素的路段划分方法不同，此方法依据高速公路主线交通运行特性和功能，将立交净距中受加、减速车流影响的部分拆分，并分别合并到加速区与减速区中，即车辆从匝道进入加速车道至正常在高速公路主线行驶为止的距离属于车辆加速影响区，其包括加速车道及其影响范围的长度。减速影响区的定义与其类似，为分流车辆在高速公路主线开始减速到分流匝道处的距离。在加、减速影响区间的路段应能完成车辆换道至目标车道的操作。为保证高速公路交通运行的安全，各功能区的车流需在不受其他区域车流的影响并不产生交织影响的情况下完成指定的驾驶任务。在高速公路互通立交设置突破规范要求时，进入高速公路主线的车辆至少在加、减速影响区之间完成车辆加速、换道至主线的驾驶任务；而驶离主线的车辆至少应在完成由内侧车道向外侧车道换道及减速后，完成换道并安全驶入匝道的驾驶任务。如果换道车辆已在相应标志表现指引下提前完成换道任务，并分离通过型车流和分/合流车流，互通立交间距可进一步突破极限间距。因此，在满足行驶规定并设置相应管控措施的情况下，高速公路匝道极限间距为：各功能区为使驾驶员能安全完成最低驾驶任务要求所需设置的最小长度之和。

图2 多车道高速公路匝道间车辆行为及对匝道的划分Fig.2 Driving behaviors between ramps of multi-lane expressway and related partitioning of ramp spacing

车辆加速影响区处，车辆进入加速车道后开始加速至主线运行车速，同时判读交通标志标线信息，观察主线交通运行状况，寻找可插入间隙以期进入高速公路主线。在设置贯通的辅助车道时，车辆可最晚在出口匝道标线变为实线前完成换道驾驶行为，否则必须在加速车道结束前进入高速公路主线。国外最新研究表明车流汇入主线影响范围为加速车道与主线最外侧两个车道从加速车道开始后457.2 m[23]，但未能提供详细的沿线车速变化数据。因此可应用海量实测数据对合理的车辆加速区范围进行识别。

在车辆减速影响区处，欲驶离主线车辆在接近减速车道后，会适机换道到最外侧车道，判读出口标志标线信息，并开始减速。在主线分流鼻前应保证判断出口所需的识别视距，在匝道长度不足时，需在进入减速车道渐变段起点前设置长度为出口识别视距与出口匝道长度差值的最小安全距离。在设置贯通的辅助车道时，车辆可提前换道至辅助车道，但最晚在出口匝道标线变为实线前换道至减速车道。国外研究认为，车流驶离主线的影响范围为减速车道与主路最外侧两个车道减速分流鼻上游457.2 m[23]，但也需结合实测数据进行验证。国内规范对加减速车道的规定如表1所示。

车辆换道时主要受其所在车道的位置、车速、间隙等因素影响。位于内侧车道(车道n)的车辆在换道至出口匝道时需先换道至外侧车道(车道1)，再进入减速车道到出口匝道，因此需要较长的换道时间及换道距离。已有研究表明，双向八车道高速公路二级服务水平下，从车道4换道至车道1时经过的距离超过600 m[22]。为进一步突破极限间距，提出将驶出交通流与通过型交通流相分离的方式，使驶出交通流提前分流至外侧车道，并采用速度管理措施。根据交通流理论，车速越高时，交通量相对较低，车头间距变大，同时可接受间隙也略有增大[24]，因此可认为换道行为同车速及车辆初始位置等因素相关。

表1 国内对变速车道设置的建议

1.2 高速公路匝道间距识别模型

根据高速公路匝道间各功能区的划分，建立基于各功能区长度的匝道间距识别模型如式(1)所示。其中，将设置附加车道、隔离等交通管控措施等各因素的影响综合换算成对匝道间距所需调整的距离，并加入各功能区长度之和中，可获取最终推荐的匝道间距计算模型。

(1)

式中,L为互通立交的匝道间距;La为加速车道及其影响区域的长度;Ld为减速车道及其影响区域长度;Lc为交织换道区长度;Lo为其他影响因素的调整。

2 基于运行车速数据的加减速影响区域长度识别

2.1 运行车速特性分析方法

为获取高密度交叉环境下高速公路加减速影响区的长度，采用建立数据驱动模型的方法，对高密度高等级道路交叉处交通流的影响范围进行识别。因高精度GPS数据包含时空范围内的车速变化信息及对应车辆的三维位置信息，将GPS数据信息应用地图匹配算法投影到地理信息系统中，可叠加至特定道路上对交通特性进行分析。在所研究对象路段样本数据量较小，不足以建立数据驱动模型时，可选取具备相类似交通特性并具备足够样本数据量的路段进行分析。城市快速路同高速路交通运行环境类似，交叉密度高, 样本数据量大，因此在识别加减速影响区域长度特性时也被作为主要数据来源。

为获取道路沿线的车速变化特性，应用Oracle数据库软件编写相应SQL代码筛选出所研究方向的GPS数据。如图3所示，在ArcGIS系统中沿所研究道路方向，将道路等间距划分(加入分割点)，以分割点为中心将道路范围内的空间划分为若干方格状的基本单元，再将单位时段内位于各基本单元内的车速统计分析，可获取研究路段运行车速的时空分布特性。

图3 高速公路基本单元和对应GPS数据关系Fig.3 Elementary unit of expressway and relationship to GPS data

根据高速公路沿线车速的统计分布特性，车辆在接近互通立交时车速会有一定程度的降低，然后保持相对稳定的车速通过互通立交，经过匝道合流点后，车速逐步提升至正常水平[25]。结合道路几何线型特征及交叉点位置，分别统计道路主线基本路段平均车速，匝道分流点上游、合流点下游的车速，将车速低于主线基本路段平均车速85%的受影响匝道路段定位匝道分合流点影响范围。为消除车身长度及车辆跟驰的影响，基本单元边长取10 m，并统计各基本单元内所有有效GPS车辆的平均车速。算法具体流程如图4所示。

图4 匝道影响范围识别模型框架Fig.4 Framework of determination model for influence area of ramp

2.2 数据描述

测试数据采用了某市出租车的高精度GPS运行数据。数据信息包括出租车序号、车牌号码、GPS时间、经纬度、车辆状态、实时速度、方向等信息。车载GPS设备每隔30 s将采集信息回传至交通信息中心。对数据的初步分析表明，高速公路出租车GPS的数据样本较小，但数据偏差较小，不同天相同时段的交通运行模式基本类似。为保证高速公路测试路段拥有充足的样本量，测试数据将3个工作日相同时段类似交通条件的数据进行叠加，即采用具备相同交通特性的3 h的数据进行分析，而快速路仅采用所测试的1 h的数据。测试时仅选用出租车正常运行的状态(空车、重车)时的数据。为判断两种状态的差异性，对其进行假设检验分析的结果表明：在快速路主路及高速公路上，空车与重车的出租车在运行车速上不存在明显差异。

图5 所选择测试道路几何线型及沿线车速分布(单位:km/h)Fig.5 Road geometry and distribution of GPS floating car speed data of selected road sections(unit:km/h)

为测试极限状态下车辆的运行特性，选用某市绕城高速两小间距互通间运行的车辆车速进行测试，同时选取相同城市快速路两相邻互通立交间的车速数据类比。城市快速路采用主辅路形式，在两互通立交间存在两处主辅路连通匝道，且一日内存在各种交通状态，适于测试极限状态下各匝道间的交通流运行特性。测试路段基本特性如表2所示。

表2 所选用测试路段基本信息

注：城市快速路主线中途靠近互通处，各设置一组分流车道及合流车道连接主辅路，本文取间距最短的一组入口-出口型匝道间距。

2.3 高速公路交叉影响区域长度识别

应用GIS系统显示所选择高速公路路段车速的空间分布如图5所示，采用2.1节中方法，统计合流点和分流点后各道路基本单元的平均车速，将车速低于主线基本路段平均车速85%的基本单元定为影响区域。汇总合流点和分流点的影响范围及对应的基本路段平均车速的统计结果如表3所示。统计结果显示，绕城高速公路的平均车速高于所测试的城市快速路段，但车流量较小，服务水平高。分流交通流对主线的影响范围要比合流交通流对主线的影响范围大。交叉段主线速度越大，匝道出入口受影响范围越长。对分流点及合流点的车速与影响范围的拟合分析如图6及图7所示，其结果显示影响范围与车速近似呈线性关系，加速车流及影响距离为分流点鼻端下游距离La，减速车流及影响范围为合流点鼻端上游距离Ld，其计算公式分别如式(2)、(3)所示：

La=1.654 9v+26.172，

(2)

Ld=1.359 2v+20.963，

(3)

式中v为道路主线基本路段的平均车速。

图6 合流点影响范围与速度关系图Fig.6 Releation between influence area of merging point and approaching speed

图7 分流点影响范围与速度关系图Fig.7 Releation between influence area of diverging point and approaching speed

3 基于换道行为的管控下交织换道段极限长度模型

3.1 极限状况所采用的管控措施

为保证交织换道段车流运行的安全和效率，对多车道高速公路(双向六车道及以上)的通过型车流与合/分流车流采用如图8所示的物理分隔措施，提前引导合/分流车流至交织换道区，并采用相应限速措施。根据交织换道区是否设置辅助车道，对交织换道区的车道划分进行分析。因在交织换道区对高速公路限速，当未设置贯通的辅助车道时，交织换道区需至少保留一条正常行驶车道及一个紧急停车带，在设置辅助车道时，可保证至少两条正常行驶车道。依此设计，通过型车流可至少有两条正常行驶车道。

表3 观测的基本路段车速及影响范围

在未设置辅助车道时，合流车辆需首先汇入分流车流，再依次行驶，直至分流车辆驶入减速车道。采用此类设计时，在交通量较大时需在合流点处采用匝道控制措施，同时需保证驶出匝道不会发生交通拥堵。在设计辅助车道时，合流车辆及分流车辆在此区段内完成交织换道即可完成分流及合流。通过上述分析可见，虽不设置辅助车道可采用较短的匝道间距，但其不适用于较大流量的情况，因极限状况下匝道间距一般较短，可将加减速车道贯通并设置为辅助车道，以提升交通运行效率。

图8 极限状态下的交通管控措施Fig.8 Traffic management and control measures under ultimate condition

3.2 基于换道行为的交织换道段极限长度识别

在未设置辅助车道时，车辆禁止换道，因此仅需保证足够的加速距离及排队距离。在设置贯通性辅助车道时，需识别交织换道段的长度。在采用上述管控措施时，车辆完成驾驶目的需进行一次换道。此时，车辆需经过等待可插入间隙、驾驶员判断及平行行驶、车辆横移等阶段来完成驾驶行为。通过对每个阶段所需时间进行建模，可获取交织换道段必需长度如式(4)所示。式中每阶段所需时间的计算如表4所示。式中增加设置安全系数θ，其取值范围可为1.0～1.3。当设计车速限为80 km/h，服务水平为二级，取θ=1.1时，按上述计算模型计算得出此时交织换道区的距离不应小于639 m。

(4)

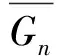
表4 等待可插入间隙计算公式

注：tw的计算受车辆到达的分布影响。当车辆到达服从泊松分布，设车头时距服从移位二阶爱尔朗分布，gm为车头时距最小值(设为1.3 s)，t为时间，λ为单位时间到达率，ga为车辆可插入临界间隙(设为3.5 s)时，平均等待时间可表示为:

4 对极限匝道间距设置的讨论

根据式(2)及式(3)计算可得，在高速公路限速为80 km/h时，加速影响区长度约为159 m，减速影响区长度约为130 m。假设在设置相应管控措施后，在二级服务水平下，所有车辆均可顺利完成换道行为，此时其他因素的调整距离L0取0 m，由此可得在上述道路交通环境下，高速公路匝道间距最少需满足928 m，将其扩大取整，按取930 m进行讨论。按国内相关技术标准规定，取加减速车道长度均为245 m，可得传统的立交净距约为440 m，小于交织换道区域长度639 m，可见车辆需提前汇入高速公路主线。

在设计过程中，如出现互通立交空间距离不足的情况时，可在采用限制车速及分离主线通过型交通流的基础上部分缩短交织换道区的长度,即可在保证交通运行安全的基础上，进一步降低安全系数的方法以减少互通间距。例如在计算交织换道段距离时，采用了θ=1.1的安全系数。如果确认所设置的措施能保证交通运行安全，可将安全系数θ取值为1，此时交织换道区长度可进一步缩短为581 m。需要注意，为保证交通运行的安全及效率，建议安全系数θ的取值应大于1，仅在充分论证其安全状况时方可取值为1。在此情况下，交织换道区长度可减少58 m，因此所测试的高速公路极限匝道间距进一步降为872 m。国内规范规定，高速公路互通立交间距一般不小于4 km，在互通立交间距突破规范时，一般采用立交净距评价，其最小立交净距为1 000 m，极限状况不得低于600 m。论文在采用了额外的交通管控措施后，进一步降低了交织换道区的长度。虽然论文计算值显示可突破极限值600 m，但论文不建议其小于640 m，并需严格执行相关管控措施。

论文所提出的管控措施主要面向双向六车道及以上的高速公路。对于双向四车道的高速公路，仍建议遵循已有的道路设计规范值。在实际应用过程中，如果有需突破极限立交净距的情况，建议考虑采用复合式立交等形式进行设计。

5 结论

(1)结合高速公路不同组成部分特性，将高速公路互通立交极限间距的求解转换为用匝道间距表示，并根据交通数据特性将其进一步划分为加、减速影响区及交织换道区。为进一步突破匝道极限间距，采用了增加管控措施的方案，建立了基于GPS车速数据驱动及间隙接受理论的极限匝道间距识别模型，对指定运行条件下互通立交间匝道的极限间距进行计算及建议。

(2)在采用分离主线通过型交通流，交织换道区限速80 km/h，设置辅助车道等交通措施时，二级服务水平下的极限匝道间距为872 m，其中加速影响区长度为159 m，减速影响区为长度130 m，交织换道区长度为581 m。实际应用中，建议对交织换道区长度乘以大于1的安全系数。加速影响区的影响范围大于减速影响区。

(3)GPS数据所采集的环境未对车道进行分离，部分匝道属于城市快速路的直通式主辅路接入，与匝道运行特性有所差异。论文在进行数据选取时，选取了与所设想环境尽可能相似的测试环境，并针对性地选取了受影响车辆的运行数据。在下一步工作中，应进一步消除数据的波动性，构筑类似环境的平台进行测试。

[1] PARK B J, FITZPATRICK K, LORD D. Evaluating the Effects of Freeway Design Elements on Safety [J]. Transportation Research Record, 2010, 2195: 58-69.

[2] YU L, LI Z, BILL A R, et al. Development of Freeway and Interchange Safety Performance Functions with Respect to Roadway Lighting[J]. Transportation Research Record, 2015, 2485:16-25.

[3] 刘伟铭, 邓如丰, 张阳，等. 高速公路出匝分流区超车道车辆车道变换模型[J]. 公路交通科技, 2012, 29(8):106-111.

LIU Wei-ming, DENG Ru-feng, ZHANG Yang, et al. Vehicle Lane-changing Model for Overtaking Lane in Freeway off-ramp Diverging Area[J]. Journal of Highway and Transportation Research and Development, 2012, 29(8):106-111.

[4] WANG R, HU J, ZHANG X. Analysis of the Driver’s Behavior Characteristics in Low Volume Freeway Interchange [J]. Mathematical Problems in Engineering, 2016,1208:1-9

[5] WOOD J S, DONNELL E T, PORTER R J. Comparison of Safety Effect Estimates Obtained from Empirical Bayes Before-After Study, Propensity Scores-potential Outcomes Framework, and Regression Model with Cross-sectional Data [J]. Accident Analysis & Prevention, 2015, 75:144-154.

[6] LEE C W. GPS Data Application for Traffic Flow Analysis [J]. Journal of the Korean Society of Civil Engineers, 2005, 25 (2D): 241-241.

[7] CHEN S, MAO B, LIU S, et al. Computer-aided Analysis and Evaluation on Ramp Spacing Along Urban Expressways [J]. Transportation Research Part C: Emerging Technologies, 2013, 36(11): 381-393.

[8] LE T Q, PORTER R J. Safety Evaluation of Geometric Design Criteria for Spacing of Entrance-Exit Ramp Sequence and Use of Auxiliary Lanes [J]. Transportation Research Record, 2012, 2309: 12-20.

[9] SHEA M S, LE T Q, PORTER R J. Combined Crash Frequency-Crash Severity Evaluation of Geometric Design Decisions: Entrance-Exit Ramp Spacing and Auxiliary Lane Presence [J]. Transportation Research Record, 2015, 2521: 54-63.

[10]龙科军, 杨晓光, 王跃辉，等. 城市快速路匝道最小间距模型[J]. 交通运输工程学报, 2005, 5(1): 106-110.

LONG Ke-jun, YANG Xiao-guang, WANG Yue-hui, et al. Models for Determining Minimum Distance of Ramps on Urban Expressway [J]. Journal of Traffic and Transportation Engineering, 2005, 5(1): 106-110.

[11]Transportation Research Broad. Highway Capacity Manual 2010 [M]. Washington, D.C.: National Academy of Sciences, 2010.

[12]RONCOLI C, PAPAGEORGIOU M, PAPAMICHAIL I. Traffic Flow Optimisation in Presence of Vehicle Automation and Communication Systems-Part I: A First-order Multi-lane Model for Motorway Traffic [J]. Transportation Research Part C: Emerging Technologies, 2015, 57: 241-259.

[13]RONCOLI C, PAPAGEORGIOU M, PAPAMICHAIL I. Traffic Flow Optimisation in Presence of Vehicle Automation and Communication Systems-Part II: Optimal Control for Multi-lane Motorways [J]. Transportation Research Part C: Emerging Technologies, 2015, 57: 260-275.

[14]American Association of State Highway and Transportation Officials. A Policy on Geometric Design of Highways and Streets [M]. 5th ed. Washington,D.C.: American Association of State Highway and Transportation Officials, 2004.

[15]American Association of State Highway and Transportation Officials. A Policy on Arterial Highways in Urban Areas [M]. Washington,D.C.: American Association of State Highway and Transportation Officials, 1957.

[16]American Association of State Highway and Transportation Officials. A Policy on Geometric Design of Rural Highways [M]. Washington,D.C.: American Association of State Highway and Transportation Officials, 1965.

[17]CHEN H, LU L, LU J J, et al. Development and Applications of Models of Average Speed in the Combination Area of Urban Expressway Ramps [J]. Advances in Transportation Studies, 2015, 35(7): 19-42.

[18]FITZPATRICK K, PORTER R J, PESTI G, et al. Guidelines for Spacing between Freeway Ramps [J]. Transportation Research Record, 2011, 2262: 3-12.

[19]ZHAO J, MA W, LIU Y, et al. Optimal Operation of Freeway Weaving Segment with Combination of Lane Assignment and On-ramp Signal Control [J]. Transportmetrica A: Transport Science, 2016, 1-50.

[20]LI Y, CHEN K M, GUO X C. Impact of Stretching-Segment on Saturated Flow Rate of Signalized Intersection Using Cellular Automation [J]. Journal of Central South University, 2013, 20 (10): 2887-2896.

[21]LI Y, LI K, TAO S, et al. Optimization of the Design of Pre-Signal System Using Improved Cellular Automaton [J]. Computational Intelligence & Neuroscience, 2014, 2014: 926371.

[22]吴明先, 潘兵宏, 王佐，等. 八车道高速公路互通式立交最小净距计算模型 [J]. 长安大学学报：自然科学版, 2012, 32(4): 31-37.

WU Ming-xian, PAN Bing-hong, WANG Zuo, et al. Calculation Model of Minimum Net Distance between Interchanges on Eight-lane Expressway [J]. Journal of Chang'an University: Natural Science Edition, 2012, 32(4): 31-37.

[23]ROESS R P, PRASSAS E S. The Highway Capacity Manual: A Conceptual and Research History [M]. New York: Springer International Publishing, 2014.

[24]DELIS A I, NIKOLOS I K, PAPAGEORGIOU M. Macroscopic Traffic Flow Modeling with Adaptive Cruise Control: Development and Numerical Solution [J]. Computers & Mathematics with Applications, 2015, 70 (8): 1921-1947.

[25]赵晓翠, 杨峰, 赵妮娜. 高速公路互通立交分流区的驾驶行为 [J]. 公路交通科技, 2012, 29 (9): 143-145.

ZHAO Xiao-cui, YANG Feng, ZHAO Ni-na. Driving Behavior in Diverging Area of Expressway Interchange[J]. Journal of Highway and Transportation Research and Development, 2012, 29(9): 143-145.

Determination of Ultimate Expressway Ramp Spacing Based on GPS Floating Car Speed Data Driven Model

WANG Fan1，LI Yan1,2，LIU Jian-bei2，LI Yuan1，XIA Li-pin1

(1.School of Highway, Chang’an University, Xi’an Shaanxi 710064, China;2.CCCC First Highway Consultants Co.,Ltd., Xi’an Shaanxi 710075, China)

The ultimate expressway ramp spacing can be determined by the proposed GPS floating car speed data driven model and gap acceptance model. A ramp spacing is divided into acceleration influence area, deceleration influence area, and lane-changing weaving area. A GPS floating car speed data driven model is established to identify the acceleration and deceleration influence areas. And the influence area of weaving area under ultimate traffic management condition is established by using gap acceptance theory. The spatio-temporal GPS speed data of taxis of a city on the specific period on test road section are analysed. The result indicates that the lengths of acceleration and deceleration influence areas are linear to vehicle speed. It is proposed that to separate the throughput flow and diverted/merged flow on multi-lane expressway. The estimation of gap acceptance model indicates that the lengths of lane-changing weaving area should be longer than 639 m. When the throughput flow is separated, the speed of the weaving area is limited to 80 km/h, and when an auxiliary lane is set, the ultimate expressway ramp spacing is 872 m under level of service II, and it is suggested to be longer than 930 m for the concern of safety.

traffic engineering; ultimate ramp spacing of multi-lane expressway; data driven model; gap acceptance theory; GPS floating car data; expressway management and control

2016-02-17

国家自然科学基金项目(51408049); 中国博士后科学基金项目(2016M590914); 陕西省自然科学基础研究计划项目(2015JQ5167); 广东省交通运输厅科技项目(2014-02-012); 中央高校基本科研业务费专项资金项目(310821161011, 310821161017)

汪帆(1989-)，女，陕西西安人，博士研究生.(wfssjj@chd.edu.cn)

10.3969/j.issn.1002-0268.2016.09.020

U412.36

A

1002-0268(2016)09-0127-09