连续可微向量场的庞加莱截面映射*
2016-11-29孙玉泉
文 晓,孙玉泉
(北京航空航天大学)
连续可微向量场的庞加莱截面映射*
文 晓,孙玉泉
(北京航空航天大学)
庞加莱截面映射是常微分方程定性理论与微分动力系统中的一个重要概念,它可以将一个连续可微向量场的问题转化为一个可微映射的问题来研究. 该文对庞加莱截面映射的存在性给出了一种新的证明方法, 通过该方法可以关于庞加莱截面映射的定义域大小给出一种一致性的刻画.
C1向量场;庞加莱截面;庞加莱截面映射;隐函数定理
1 可微向量场的庞加莱截面映射
庞加莱截面映射是使用定性方法研究常微分方程以及微分动力系统中的一个重要工具,来源于19世纪庞加莱关于天体力学的一系列工作.在常微分方程的渐进稳定性研究以及微分动力系统的结构稳定性研究等数学领域中发挥着至关重要的作用,同时也广泛应用于各种自然科学研究以及工程问题当中.在该文中,介绍一种更广义的截面映射,并重点关注庞加莱截面映射定义域的大小.
设G是n维欧式空间Rn中的一个开区域, X:G→Rn是G上定义的一个C1向量场,则由微分方程解的存在唯一性定理[2],自治微分方程
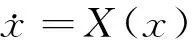
(1)
满足初始条件x(t0)=x0的解是存在且唯一的.记这个解为x=φ(t)=φ(t;t0,x0),为讨论起来简便,这里不妨设每个解都可以延拓到t∈(-∞,+∞).把t看成参数,则φ(t;t0,x0)确定了G中的一条曲线,一般将它称为方程(1)的一条轨线. 特别地,如果记φt(x0)=φ(t;0,x0),则由解对初值的可微依赖性,{φt}中的每一个φt都是G到G的一个微分同胚,并满足条件[3]:
(a) φ0=Id; (b)φt+s=φt∘φs.
这时{φt}一般称之为一个流或一个连续(时间)动力系统.
设x是向量场X的一个常点,即满足X(x)=0的点,则在x点处可以取一个n-1维的超平面Nx,使得X(x)是Nx的法向量. 记Nx(r)={y∈Nx:|y-x|
不难注意到,庞加莱截面上不能含有向量场X的奇点(即满足X(x)=0的点). 对于庞加莱截面映射Px,T,当x靠近奇点的时候,其定义域会变得很小. 那么庞加莱截面映射的定义域到底能做到多大,是否与向量场在该点的长度有联系?这个问题在经典的微分方程定性理论以及微分动力系统的教材(如文献[1,3,6])中都没有给出回答. 在该文中,将对这一问题进行讨论,给出如下结论.
定理1 关于方程(1),如果在凸区域G上X(x)的导数有界,即存在一个常数K>0,使得‖DX(x)‖
在常规的庞加莱截面映射存在性的证明中, 使用的是一般形式的隐函数定理,这时可以得到当y离x足够近的时候截面映射的存在性, 一般不能得到庞加莱截面映射的定义域的大小信息. 因此这里需要进行更细致的观察,回顾一般隐函数定理的证明,当采用压缩映射原理来证明隐函数定理时,根据压缩映射定理成立的条件,往往能得到定义域大小的信息. 因此,在文中将采用压缩映射定理进行讨论.
2 定理1的证明
首先对庞加莱截面的大小进行刻画. 有如下的引理成立:
引理1 关于方程(1),如果在凸区域G上X(x)的导数有界,即存在一个常数K>0,使得‖DX(x)‖ 证明 易见X(y)不平行于Nx等价于〈X(y),X(x)〉≠0(其中〈·,·〉表示向量的内积). 因此只需寻找η1,使得任取常点x∈G,以及任取y∈Nx(η1|X(x)|),就有〈X(y),X(x)〉>0成立.本 首先注意到,只需 |X(y)-X(x)|2<|X(x)|2 就会有〈X(y),X(x)〉>0.这是因为若 |X(y)-X(x)|2=|X(y)|2-2〈X(y),X(x)〉+|X(x)|2<|X(x)|2 成立,则有 |X(y)|2-2〈X(y),X(x)〉 <0 故〈X(y),X(x)〉>0. 由于‖DX(x)‖ |X(x)-X(y)|=|DX(ξ)(x-y)|≤ K|x-y| 成立. 取η1=1/(2K), 则当|x-y|< η1|X(x)|时, |X(x)-X(y)|≤K|x-y|≤Kη1|X(x)|=(1/2)·|X(x)|<|X(x)| 因此当y∈Nx(η1|X(x)|)时,|X(y)-X(x)|2<|X(x)|2,从而就有X(y)不平行于Nx. 引理1证毕. 回顾庞加莱截面映射的定义, 为证明定理1, 只需找到常数η<η1, 使得当|x-y|< η|X(x)|时, 存在时间τ=τ(y), 使得φτ(y)(y)∈Nz. 易见φτ(y)(y)∈Nz等价于向量φτ(y)(y)-z垂直于向量X(z),即 〈φτ(y)(y)-z,X(z)〉=0. 构造函数F(t,y)=〈φt(y)-z,X(z)〉. 由z=φT(x)可见F(T,x)=0. 又通过简单的计算可知 (2) 证明 假设引理的结论不正确,存在 下面回到定理1的证明, 由于‖DX(x)‖ |φT(y)-z|≤eKT|y-x|≤ 有 ρ(G(φ0),φ0)=max|G(φ0)(y)-T|=max|-|X(z)|-2F(T,y)|=max|X(z)|-2× 由定理1可见,如果考虑的是一个有界闭区域上连续可微的向量场,虽然庞加莱截面映射的定义域做不到一致的尺寸,但至少可以找到一个一致常数η, 使得庞加莱截面映射在半径为η|X(x)|的圆盘内有定义. 特别地,将这个结论应用到紧致无边流形上的连续可微向量场时,导数有界是天生成立的,因此必然存在类似的一致常数η. 在廖山涛先生使用典范方程组研究含奇点流的工作中[4-5],蕴含了这里的结论. 但由于廖山涛先生在论文中采用的工具是典范方程组理论,而不是西方学者所常用的流盒(又称管状邻域)的办法[6],因此相应的结论不被外界所熟知. 笔者的结论对庞加莱截面映射的定义域给了一个明确的大小,特别是在靠近奇点的时候,虽然知道庞加莱截面映射的定义域非常小,但是它大小的阶可以做到向量场同阶.可以预计这些结论在对含奇点流的研究中能起到一定的作用. [1] Hirsch M, Smale S, Devaney R. 微分方程、动力系统与混沌导论:第2版[M]. 甘少波译. 北京:人民邮电出版社, 2008.1-336. [2] 丁同仁,李承治. 常微分方程教程[M]. 北京:高等教育出版社, 2004.1-384. [3] 张锦炎,冯贝叶. 常微分方程几何理论与分支问题[M]. 北京: 北京大学出版社, 2005.1-431. [4] 廖山涛. 典范方程组[J]. 数学学报, 1974, 17(2): 100-109. [5] 廖山涛. 常微系统的某些一致性质及一个周期轨道存在定理的推广[J]. 北京大学学报:自然科学版, 1985(2), 1-19. [6] Palis J, Melo W D. Geometric Theory of Dynamical Systems: An Introduction[M]. New York: Springer, 1982.1-198. (责任编辑:于达) Poincaré Section Map for C1Vector Fields Wen Xiao, Sun Yuquan (Beihang University) In the article, a description of Poincaré section map for LipschitzC1vector fields on is given. The size of definition domain of the Poincaré section map will be uniform in some sense. It is a deep application of Implicit Function Theorem. C1Vector Fields; Poincaré Section; Poincaré Section Map; Implicit Function Theorem 2016-03-22 *国家自然科学基金(11301018);北京航空航天大学教学改革基金资助 O175 A 1000-5617(2016)02-0012-04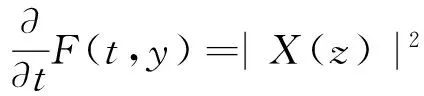
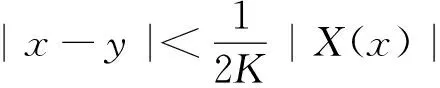
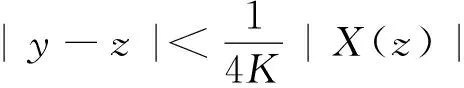
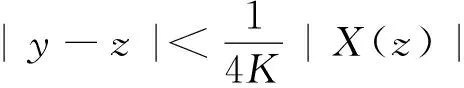
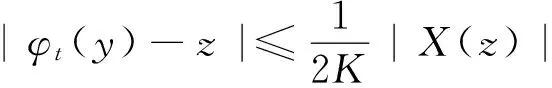
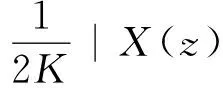

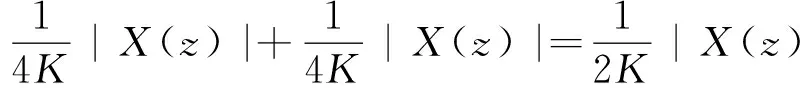
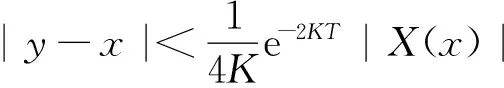
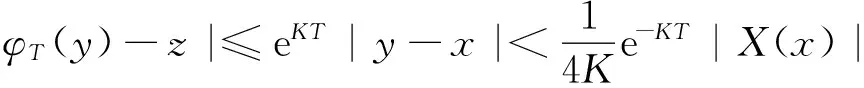
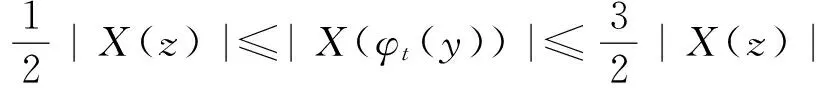
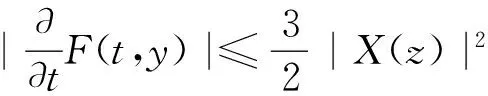
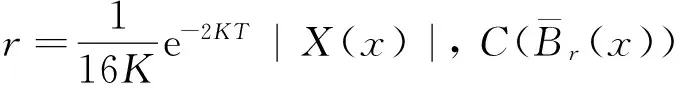

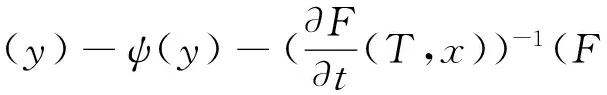
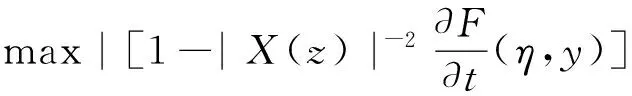
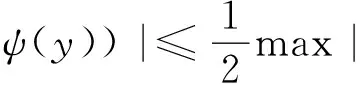

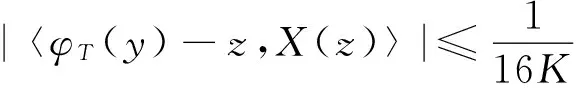
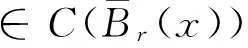
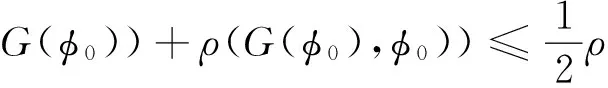
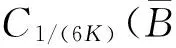
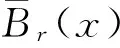
3 结束语
