一类布尔函数的代数免疫度的下界

2016-11-29田叶张玉清胡予濮伍高飞

通信学报 2016年10期

关键词：下界码字正整数

田叶，张玉清,2，胡予濮，伍高飞

(1. 西安电子科技大学综合业务网理论及关键技术国家重点实验室，陕西西安 710071；2. 中国科学院大学国家计算机网络入侵防范中心，北京 101408)

一类布尔函数的代数免疫度的下界

田叶1，张玉清1,2，胡予濮1，伍高飞1

(1. 西安电子科技大学综合业务网理论及关键技术国家重点实验室，陕西西安 710071；2. 中国科学院大学国家计算机网络入侵防范中心，北京 101408)

代数免疫度是衡量布尔函数抵抗代数攻击的重要指标。最近，Mesnager等研究了布尔函数的零化子与函数所对应循环码最小距离之间的联系，代数免疫度的下界可以由对应的循环码的最小距离得到。解决了Mesnager提出的一个公开问题，给出了一类特定函数的零化子次数的下界，并得到一类布尔函数的代数免疫度的下界。

密码学；布尔函数；零化子；代数免疫度；循环码；最小距离

1 引言

2003年，Courtois和Meier[1]在欧洲密码学年会上提出了一种针对布尔函数的代数攻击方法，对基于线性反馈移位寄存器的流密码构成了极大的威胁，这种方法的主要原理是建立初始密钥和输出密钥流比特之间的代数方程，通过线性化方法求解该超定的多变元非线性方程组以得到初始密钥。为了衡量布尔函数抵抗代数攻击的能力，代数免疫的概念也随即被引出[1]。为了抵抗代数攻击[1～3]，流密码系统中使用的布尔函数需要尽可能具有高的代数免疫度。

国内外学者对具有最高代数免疫阶的布尔函数进行了深入的研究[1～13]。Courtois和 Meier[1]证明了n元布尔函数的最大代数免疫度是，达到此上界的布尔函数称为具有最优代数免疫度的函数。Dalai[4]首次构造了偶数元的具有最优代数免疫的布尔函数。Carlet和Feng[6]构造了一类平衡的具有最优代数免疫度的布尔函数。2010年，Rizomiliotis[7]给出了一个关于布尔函数具有最优代数免疫度的充要条件。最近，Mesnager[13]研究了布尔函数的零化子与循环码之间的关系，将对布尔函数零化子的研究转化为对所对应循环码的最小距离的研究，为研究布尔函数的代数免疫提供了一种新方法。

本文解决了 Mesnager提出的一个公开问题，给出了一类特定函数的零化子的次数下界，并得到一类布尔函数的代数免疫度的下界。

2 预备知识

本节介绍将要用到的循环码和布尔函数相关的一些基础知识。

2.1 循环码

循环码是一类重要的线性码，在通信系统、存储设备中有着广泛的应用[14～19]。

设n为正整数，记F2为含有2个元素的二元域，F2n为F2上的n维向量空间，F2n为含有2n个元素的有限域。

设n、k、d分别为正整数。记C是参数为[n, k, d]的线性码，其中，码C的长度为n，码C最小距离为d，维数为k。若对C中的任意码字进行循环移位后仍然是C的码字，则C称为循环码。

定理1[14](BCH界)α为域上的本原元。设

C是循环码，其生成多项式为g( x)，对于一些整数d≥0,δ≥ 1，满足

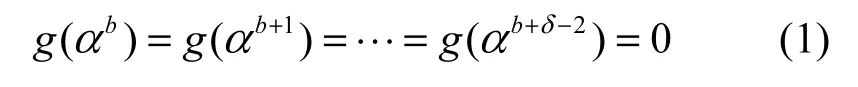
也就是说码C有（δ−1）个α的相邻幂作为零点，则码C的最小距离d≥δ。

2.2 布尔函数

在密码学中，最常用的表达布尔函数的形式是代数正规型(ANF)，表达式如式(2)所示。

其中，“⊕”表示 F2上的加，αu∈F2，u=(u1,u2,…,un)，函数f( x)的代数次数定义为代数正规型中系数不为零的次数最高的乘积项中变元的个数，即，记为deg f。代数次数小于等于1的布尔函数称为仿射函数。

布尔函数f( x)也可以看成是从F2n到F2的一个映射，它可以唯一地表示为

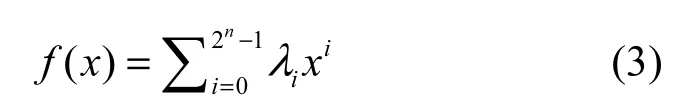
定义1[1]令f( x)∈F2n，如果存在一个非零的函数g( x)∈F2n，使f( x) g( x)=0，那么称g( x)是f( x)的零化子。函数 f( x)的代数免疫度AI( f)定义为f( x)与f( x)+1的零化子的最小次数。

本文标记MDA( f)为函数f的零化子的最小次数，MDA(f+1)为函数f+1的零化子的最小次数。因此f(x)的代数免疫度可以记为

3 主要结果

布尔函数在编码理论中具有重要的作用[13,20～22]。例如一类著名的二元码Reed-Muller码就可以通过布尔函数获得。最近，Mesnager等[13]把对布尔函数零化子的研究转化为对循环码的研究，为研究代数免疫提供了一种新方法。本节详细介绍了Mesnager提出的公开问题的具体方法。首先介绍一些关于循环码和代数免疫关系的已有的结论，更多的细节见文献[13]。

定义 2[13]记S为F2n的一个子集，任意x∈S

推论1[13]记S⊂F2n，则C( S)为长度为2n的线性码，为长度2n−1的循环码。

记g∶ F2n→F2为F2n上布尔函数f的零化子，g( x)可以表示为，其中，对于根据零化子的定义，当任意x∈supp(f )，g( x)=。当 f(0)=1时，g(0)=0，μ0=0，g( x)=。因此，为的一个码字。记。但并不是中的每一个码字都能对应函数 f的一个零化子。本文记B为的集合，其中，，且满足时，

推论2[13]布尔函数f∶F2n→F2且满足f(0)=1，那么集合与函数 f的零化子一一对应。

定理2[13]设函数f∶F→F满足 f(0)=1，记2n2δ为的最小距离。设d为满足不等式的最小正整数，则MDA( f)≥d。

定理 3[13]设函数f∶F→F满足f(0)=0，2n2记δ为的最小距离。设d为满足不等式的最小正整数，则MDA( f)≥d−1。

定理 4[13]设函数f∶F→F，记δ为2n2的最小距离，记δ′为的最小距离。p为满足不等式的最小正整数，p′为满足不等式的最小正整数。因此，集合Sf对应的布尔函数的代数免疫度AI( f)具有如下的下界。

1) 如果f(0)=1，则AI( f)≥min(p,p′−1)。

2) 如果f(0)=0，则AI( f)≥min(p−1,p′)。

设b和δ为 2个非负整数。记V(α,b,δ−1)={αb,αb+1,…,αb+δ−2}，其中，α为F中的一个本原2n元，记N=2n−1。

文献[13]提出的公开问题具体描述如下，给定布尔函数f∶F2n→F2，t、b、k、δ均为正整数，m为与N互素的正整数，设集合Sf为

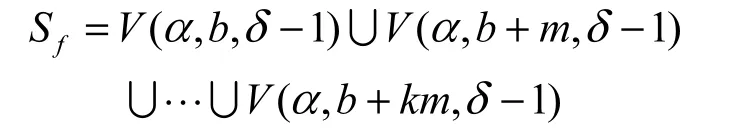
那么就存在函数1+f的零化子的最小次数的下界如何表示的问题。

注：当m≤δ−2时，V (α,b,δ−1)∪V(α,b+m,δ−1)∪…∪V(α,b+km,δ−1)=V(α,b, km +δ−1)。下文，只考虑m＞δ−2的情形。

为了解决这个问题，首先对文献[13]中的定理进行完善得到定理5。

定理5布尔函数f∶F2n→F2，假设

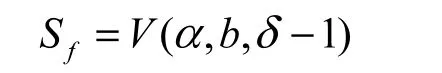
于是有：

1) 当 f(0)=1时，MDA( f)≥p；

2) 当 f(0)=0时，MDA( f)≥p−1。

证明根据定义有

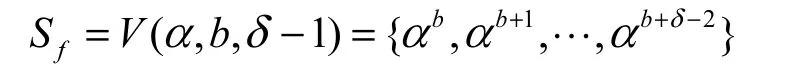
定理6对文献[13]中的定理进行了完善。

定理6布尔函数f∶F2n→F2，t、b、k、δ均为正整数，m为与N互素的正整数，假设

于是有：

1) 当 f(0)=1时，MDA( f)≥p；

2) 当 f(0)=0时，MDA( f)≥p−1。

证明根据Sf的定义，可得

设集合U为Sf中α的所有指数的集合，即式(5)中α的所有指数的集合。

设整数d0=k+δ，假设中含有重量ω小于d0的码字，即ω＜k +δ。由于为循环码，某一重量为ω的码字可以表示为下面的码多项式，其中，γ∈F ，0＜s＜N。i2ni

当 j∈U ，Pj=−1 ，前面假设ω＜k+δ，所以ω−k−1＜δ− 1，因此式(8)可以转化为

结合式(9)和式(10)，可以得出φ(1)=0，然而与φ(1)≠0是矛盾的。因此，假设ω＜k+δ是错误的，从而ω≥k+δ，也就是说中不存在任何重量ω小于k+δ的码字，即的最小距离至少为k+δ。

再根据定理2和定理3，得到定理6，即完成了证明。

定理7给出公开问题的答案，并利用证明定理6的方法对其进行证明。

定理7布尔函数f∶F2n→F2，t, b, k,δ均为正整数，m为与N互素的正整数，假设

于是有如下情况。

1) 当m(1+k)＜2n−1时

① 如果 f(0)=1，则MDA(1+f)≥p ；

② 如果 f(0)=0，则MDA(1+f)≥p −1。

2) 当m(1+k)≥2n时

① 如果 f(0)=1，则MDA(1+f)≥p ；

② 如果 f(0)=0，则MDA(1+f)≥p −1。

证明由Sf的定义可得

其中，

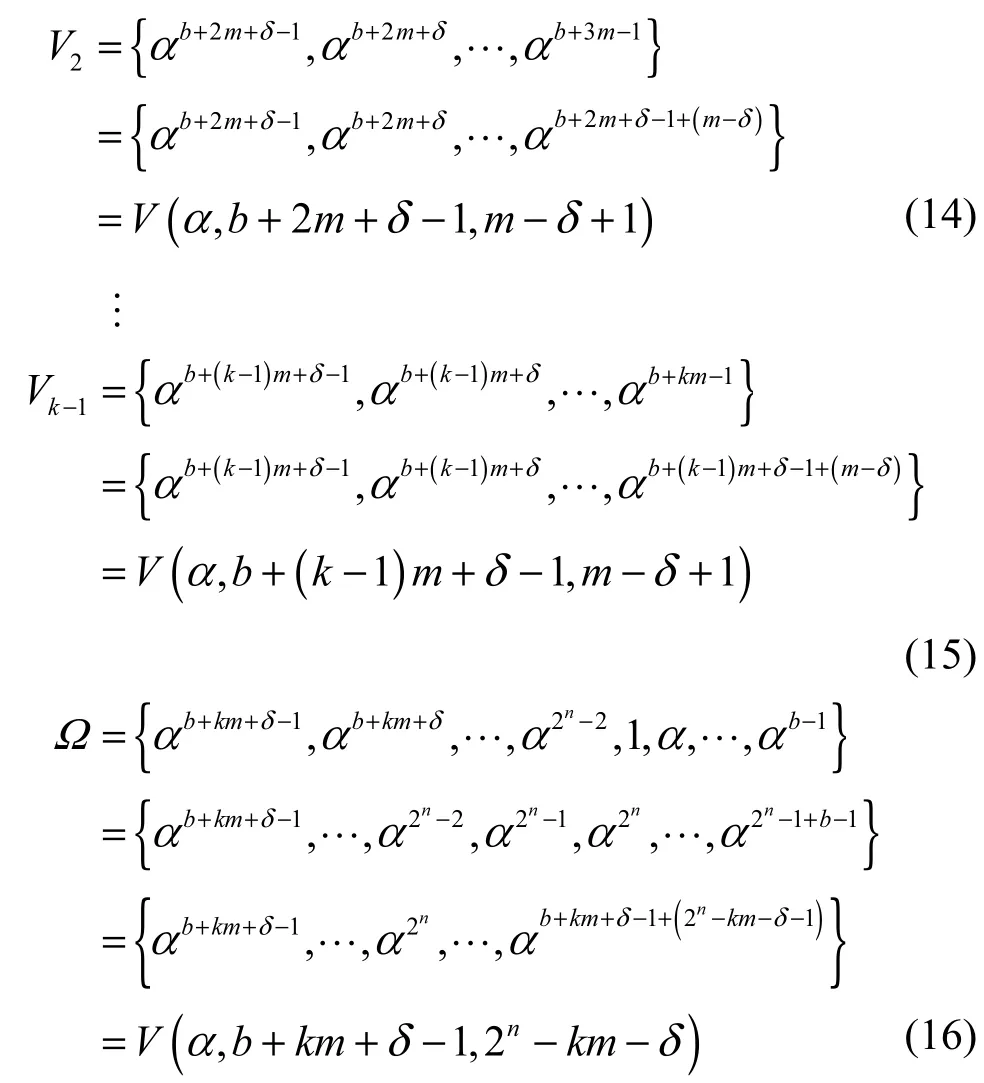
设集合U为S1+f中α的所有指数的集合，即式(12)～式(16)中α的所有指数的集合。

如果2n−km−δ=m−δ+1，则2n−1=m(1+k)，这与(m,2n−1)=1矛盾，所以2n−1≠m(1+k)。

下面分2种情况考虑。

1) 当m(1+k)＜2n−1时，设整数d=k+m−0δ+2，假设中含有重量ω小于d0的码字，即为某一重量为ω的码字的码多项式，其中，γi∈F2n，0＜si＜N。

令整数l=b+δ− 1，构造等式Ζ为

前面假设ω＜k+m −δ+2，即ω−k−1＜m −δ+ 1，并且当 j∈U，Pj=−1 ，所以式(19)也可以转化成式(21)。

结合式(20)和式(21)，可以得出φ(1)=0，然而与φ(1)≠0是矛盾的。因此，假设ω＜k+m −δ+2是错误的，从而ω≥k+m −δ+2，也就是说中不存在任何重量ω小于k+m−δ+2的码字，即的最小距离至少为k+m−δ+2。

2) 当m^(1+k)≥2n时，设整数d0=k+m−δ+1，假设C( S1+f)中含有重量ω小于d0的码字，即ω＜k+m −δ+1。令为某一重量为ω的码字的码多项式，其中，γi∈F2n，0＜si＜N。

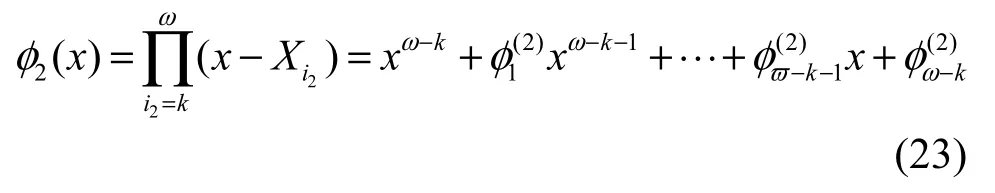
因为si≠0，(m, N)=1，所以

令整数l=b+δ− 1，构造如下的等式Ζ。

前面假设ω＜k+m −δ+1，即ω−k−1＜m −δ，当 j∈U，Pj=−1 ，所以式(24)可以转化成式(26)。

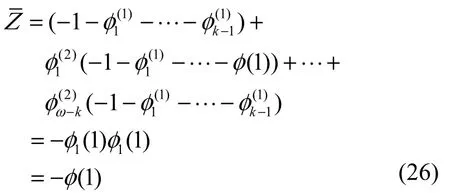
结合式(25)和式(26)，可以得出φ(1)=0，然而与前面φ(1)≠0是矛盾的。因此假设ω＜k+m −δ+1是错误的，也就是说中不存在任何重量ω小于k+m−δ+1的码字，即的最小距离至少为k+m−δ+ 1。再根据定理2和定理3，就得到了定理7。

结合布尔函数的代数免疫度的定义AI( f)=min(MDA( f),MDA(1+f ))以及定理6和定理 7，本文得到了一类布尔函数的代数免疫度的一个下界。

定理8函数f∶F2n→F2，t、b、k、δ均为正整数，m为与N互素的正整数，假设

于是有如下情况。

1) 当m(1+k)＜2n−1时

① 如果 f(0)=0，则AI( f)≥min(p, p^−1)；

② 如果 f(0)=1，则AI( f)≥min(p−1,p^)。

2) 当m(1+k)≥2n时^

① 如果 f(0)=0，则AI( f)≥min(p, p−^1)；

② 如果 f(0)=1，则AI( f)≥min(p−1,p)。

4 结束语

布尔函数在密码学中有着重要的作用。一个好的布尔函数需要具有高的代数免疫度以抵抗代数攻击。如何构造具有高的代数免疫度的布尔函数仍然是一个重要的问题。本文主要研究了布尔函数零化子与循环码最小距离之间的关系，解决了Mesnager提出的一个公开问题，即给出特定布尔函数的零化子次数的下界，并且给出了一类布尔函数的代数免疫度的下界。在未来的工作中，考虑利用一些具有优良性质的循环码来构造具有最优代数免疫度的布尔函数是非常有意义的。

[1]COURTOIS N, MEIER W. Algebraic attacks on stream ciphers with linear feedback[C]//Cryptology-Eurocrypt 2003, LNCS 2656. Berlin:Springer-Verlag, 2003: 345-359.

[2]ARMKNECHT F, KRAUSE M.Algebraic attacks on combiners with memory[C]//Cryptology-Crypto. 2003: 162-175.

[3]MEIER W, PASALIC E, CARLET C. Algebraic attacks and decomposition of Boolean functions[C]//Cryptology -Eurocrypt 2004, LNCS 3027. 2004: 474-491.

[4]DALAI D, MAITRA S, SARKAR S. Cryptographically significant Boolean functions:construction and analysis in terms of algebraic immunity[J]. Fast Software Encryption , 2005, 3557:98-111.

[5]CARLET C, DALAI D, GUPTA C. Algebraic immunity for cryptographically significant Boolean function: analysis and construction[J].IEEE Transactions on Information Theory, 2006, 52(7):3105-3121.

[6]CARLET C, FENG K. An infinite class of balanced functions with optimal algebraic immunity, good immunity to fast algebraic attacks and good nonlinearity[C]//Cryptology-Asiacrypt 2008, LNCS 5350.2008, 5350:425-440.

[7]RIZOMILIOTIS P. On the resistance of Boolean functions against algebraic attacks using univariate polynomial representation[J]. IEEE Trans Information Theory, 2010, 56(8):4014-4024.

[8]TU Z, DENG Y. A conjecture on binary string and its applications on constructing Boolean functions of optimal algebraic immunity [J]. Designs Codes and Cryptography, 2011, 60(1): 1-14.

[9]HELLESTH T, RONJOM S. Simplifying algebraic attacks with univariate analysis[C]//Information Theory and Applications Workshop(ITA). 2011:1-7.

[10]TANG D, CARLET C, TANG X. Highly nonlinear Boolean functions with optimal algebraic immunity and good behavior against fast algebraic attacks[J]. IEEE Trans Inf Theory, 2013, 59(59):653-664.

[11]LIN J, WANG M, LI Y. On annihilators in fewer variables:basic theory and applications[J]. Chinese Journal of Electronics, 2013, 22(3):489-494.

[12]欧智慧, 赵亚群, 李旭. 一类密码函数的构造与分析[J].通信学报,2013, 4(4): 106-113.OU Z H, ZHAO Y Q, LI X. Construction and analysis of one class of cryptographic functions[J]. Journal on Communications, 2013, 34(4):106-113.

[13]MESNAGER S. A note on linear codes and algebraic immunity of Boolean Functions[C]//21st International Symposium on Mathematical Theory of Networks and Systems. 2014.

[14]MACWILLIAMS F,SLOANE N. The theory of error-correcting Codes[M]. North-Holland Mathematical Library. Amsterdam, The Netherlands: North-Holland, 1977.

[15]HUFFMAN W, PLESS V. Fundamentals of error-correcting codes[M].Cambridge, UK: Cambridge Univ. Press, 2003.

[16]BETTI E, SALA M. A new bound for the minimum distance of a cyclic code from its defining set[J].IEEE Trans Information Theory,2006, 52(8):3700-3706.

[17]BETTEN A, BRAUN M, FRIPERTINGER H. Error- correcting linear codes[M]. Berlin,Germany: Springer- Verlag, 2006.

[18]GAO J, HU Y, LI X. Linear span of the optimal frequency hopping sequences from irreducible cyclic Codes[J]. Chinese Journal of Electronics, 2015, 24(4): 818-823.

[19]DING C, DU X, ZHOU A. The bose and minimum distance of a class of BCH codes[J]. IEEE Trans Information Theory, 2015, 61(5): 2351- 2356.

[20]FENG X,GONG G. On algebraic immunity of trace inverse functions on finite fields of characteristic two[J]. Journal of Systems Science and Complexity, 2016, 29(1):272-288.

[21]WU D,QI W. On the spectral immunity of periodic sequences restricted to binary annihilators[J]. Designs Codes and Cryptography,2016, 78(2):533-545.

[22]DING C.A construction of binary linear codes from Boolean functions[J]. Discrete Mathematics, 2016, 339(9): 2288-2303.

New bound of algebraic immunity of a class of Boolean function

TIAN Ye1, ZHANG Yu-qing1,2, HU Yu-pu1, WU Gao-fei1
(1. State Key Laboratory of Integrated Services Networks, Xidian University, Xi’an 710071, China;2. National Computer Network Intrusion Protection Center, University of Chinese Academy of Sciences, Beijing 101408, China)

Algebraic immunity quantified the resistance of a Boolean function to the algebraic attack. Recently, Mesnager,et al showed that there were direct linked between the annihilators used in algebraic attacks and the coding theory. They showed that the lower bound of the algebraic immunity of Boolean functions could been derived from the minimum distance of the associated cyclic codes. An open problem proposed by Mesnager is settled with a detailed proof. Also, a lower bound of algebraic immunity of a class of Boolean functions will be introduced.

cryptography, Boolean functions, annihilators, algebraic immunity, cyclic code, minimum distance

s:The National Natural Science Foundation of China (No.61572460, No.61272481), The National Key Research and Development Project (No.2016YFB0800703), The National Information Security Special Projects of National Development, The Reform Commission of China (No.(2012)1424), China 111 Project (No.B16037)

TN918

10.11959/j.issn.1000-436x.2016200

2016-05-11；

2016-08-24

国家自然科学基金资助项目（No.61572460, No.61272481）；国家重点研究计划基金资助项目（No.2016YFB0800703）；国家发展改革委员会信息安全专项基金资助项目（No.(2012)1424）；国家111计划基金资助项目（No.B16037）