单通道邻频数字调制混合信号的载波初相估计

2016-11-24杨勇郭一鸣王海昕彭华张冬玲

通信学报 2016年10期

关键词：单通道载波符号

杨勇，郭一鸣，王海昕，彭华，张冬玲

（1. 解放军信息工程大学信息系统工程学院，河南郑州 450002；2. 西南电子电信技术研究所，四川成都 610041）

单通道邻频数字调制混合信号的载波初相估计

杨勇1，郭一鸣1，王海昕2，彭华1，张冬玲1

（1. 解放军信息工程大学信息系统工程学院，河南郑州 450002；2. 西南电子电信技术研究所，四川成都 610041）

在非合作卫星通信中，针对具有固定帧长和固定帧同步序列的单通道混合信号，根据源信号间的参数差异给出一种同时适用于低阶和高阶混合信号的载波初相估计算法。算法先对去频偏后的帧同步数据以帧长为间隔进行累加，进而根据功率最大化准则对累加结果做定时同步，从而实现对初相信息的提取。为便于比较，同时推导了单通道混合信号载波初相估计的修正克拉美罗界（MCRB, modified Cramer-Rao bound）。仿真结果表明，随着累加帧数的增加，初相估计性能逐渐接近MCRB。

单通道混合；邻频干扰；载波初相估计；修正克拉美罗界

1 引言

随着数字通信业务量的增加和诸如成对载波多址（PCMA，paired carrier multiple access）[1]等先进通信体制的广泛使用，通信终端受到邻频干扰的概率不断增大。当接收信号存在邻频干扰时，通信质量会严重下降。邻频混合信号的接收包括多通道接收和单通道接收2种模式。当接收通道数不小于混合信号中源信号的个数且各个通道间不存在相关性时，采用多通道处理的方法可实现对各个源信号的有效分离。然而，由于通信终端尺寸大小的限制或者接收通道间存在较强的相关性，只能依靠一路混合信号分离出多个源信号或某个感兴趣源信号，前者称为单通道数字混合信号的盲分离问题[2～4]，后者称为单天线干扰抵消问题[5～7]。由于多通道（天线）接收价格昂贵，系统复杂，所以单通道接收逐渐成为信号处理领域的研究热点。

针对单通道混合信号的盲分离问题，目前出现了很多研究成果。其中，联合参数估计和序列检测类的研究方法是当前分离算法中的主流[8～10]，部分成果已经迈向实用化。然而，该类分离方法需要事先完成对混合信号的参数初估计，若参数估计误差较大，将可能导致分离结果发散或误收敛。一般情况下，参数估计包括各分量信号的载波频率、符号速率、幅度、载波初相和时延等估计。单通道邻频低阶数字调制混合信号（如 BPSK、QPSK等）的载频估计可通过M（M为调制阶数）次方谱的方法完成，而高阶调制混合信号的载频估计则可利用文献[11]中分级搜索的方法来实现；模方谱的方法可实现对混合信号符号速率的高精度估计；针对幅度估计问题，文献[12]根据各源信号间的幅度和频偏大小关系，基于QPSK调制的混合信号，分别提出了四次方法、MAX-MIN法和模平方法。时延估计也出现了很多研究成果[13～15]。

针对 PCMA系统中干扰信号的载波相位估计问题，文献[16]通过理论分析得到干扰信号载波相位估计的最佳长度与归一化载波剩余频率偏差的关系表达式。但其仅适用于合作通信背景下，即其中一路信号的发送序列精确已知；针对单通道邻频MPSK调制的混合信号，当各源信号的频偏存在差异时，文献[9]在完成频偏估计的条件下，通过构造辅助信号实现对载波初相信息的提取。然而，该方法适用的初相估计范围随着调制阶数的增加而变小，当超出该估计范围后，将存在相位模糊。此外，克拉美罗界（CRB，Cramer-Rao bound）是参数实现无偏估计条件下估计方差的下界，也是评价参数估计算法性能最常用的界[17]。然而，当前已有关于参数估计的 CRB或修正 CRB（MCRB，modified CRB）都是针对单一信号，该性能界显然无法用于度量混合信号参数估计的性能。

鉴于此，在非合作卫星通信背景下，针对具有固定帧长和固定帧同步序列的单通道邻频数字调制混合信号，本文从帧同步符号累加的结果中提取载波初相信息，并推导单通道同频混合信号载波初相估计的MCRB。

2 信号模型和基本假设

在卫星通信中，考虑2路MPSK或MQAM调制信号，符号周期都为T，将成型滤波器和匹配滤波器的响应总和视为等效信道滤波器的响应结果，且响应持续时间为[−L1T, L1T]（等效滤波器非因果和因果的周期均为L1），那么以（p为过采样倍数）为周期对混合信号进行采样，可得到离散形式

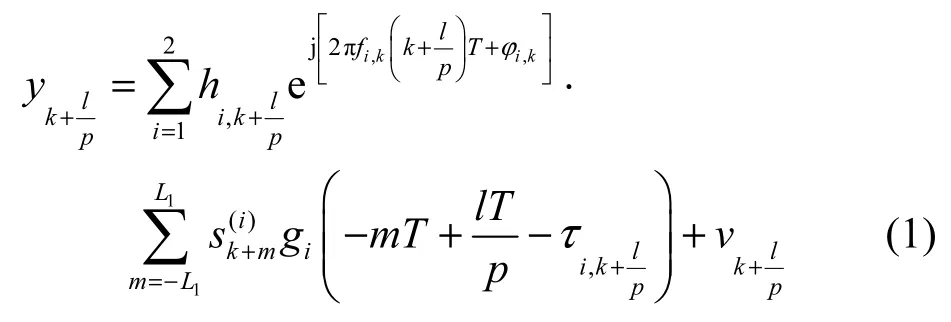
其中，l=0, …, p−1，vk是均值为0、功率谱密度为N0的加性复高斯白噪声信号在时刻的采样值；是第i(i=1, 2)路信号在k+m时刻的输入符号；和分别是第 i路调制信号在时刻的幅度、残余频偏、相偏和时延。在实际应用中，这 4个参数是缓慢时变的，为简化模型，在有限的数据范围内，假设它们都是非时变的，即此外，假设 2路信号的等效信道滤波器满足g1(t)=g2(t)=g(t)。

此外，假设发送的符号序列在同一路源信号之内和不同路源信号之间都是相互独立的，则

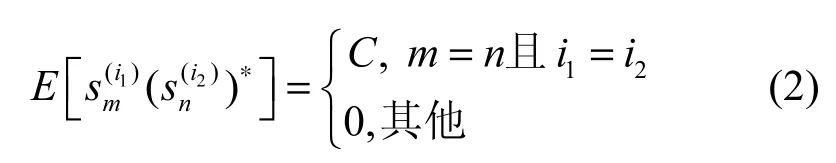
进一步，假设2路信号具有相同的符号帧长N，每一帧数据包含K个同步符号和P个数据符号，即N=K+P。以数据起点为基准，第一路信号和第二路信号同步符号的起始位置分别为 n1和n2，如图1所示。此外，当2路源信号的帧头起始位置不重叠时，称2路源信号编码异步，反之称为编码同步。

在本文的研究中，单通道邻频数字调制混合信号的载波初相估计就是仅根据接收序列yk，在已知频偏 fi和帧同步符号的条件下分别得到 φ1和 φ2的精确估计值。

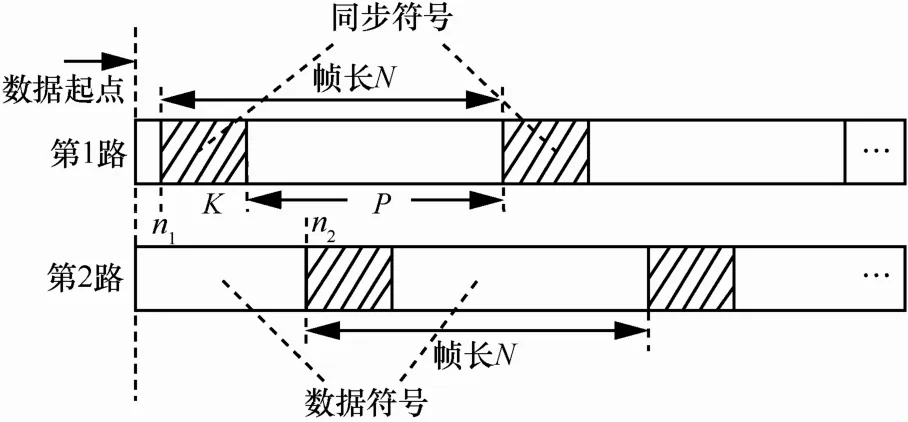
图12路信号混合情况

3 载波初相估计

3.1 帧长及帧头起始位置估计

对式(1)进行p倍抽取后，可得到以T为周期的混合信号采样数据

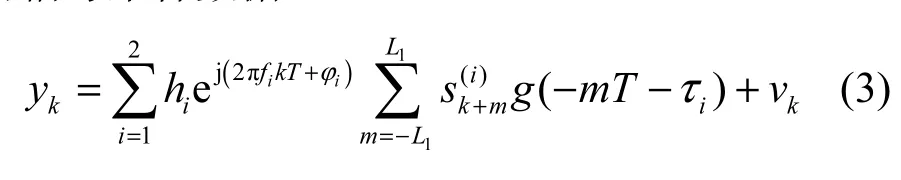
设待估帧长为ˆN，将序列{yk}以ˆN+K−1为长度单位进行分段，各个数据段之间的重叠长度为K−1。在此基础上，各个数据段之间以窗长为K个数据做滑动互相关，对结果求模后得到

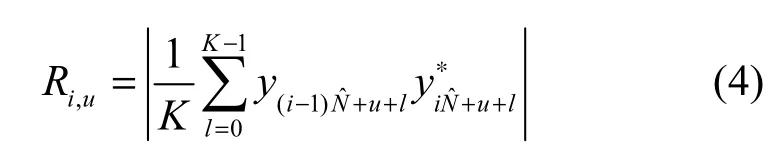
其中，Rn,u表示第 n个数据段和第n+1个数据段中第u（u=1,…,ˆN）到u+K−1个数据间互相关的模值，“*”和“|·|”分别表示复数求共轭和求模值运算。

将式(3)代入式(4)，根据不同时刻数据及不同路源信号数据之间的不相关性，式(4)可化简为

进一步，增加做互相关运算的数据段个数可以提高帧长估计的稳定性，若参加运算的数据段个数为I，则对于每一个待估帧长值Nˆ，可得到

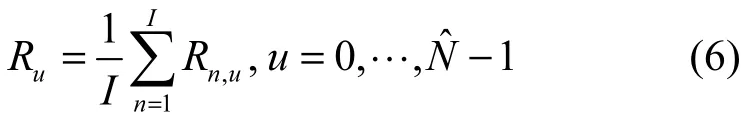
3.2 频偏不相等时的初相估计

当完成对帧长和帧头起始位置的估计后，对第i路源信号的帧同步数据构造辅助信号

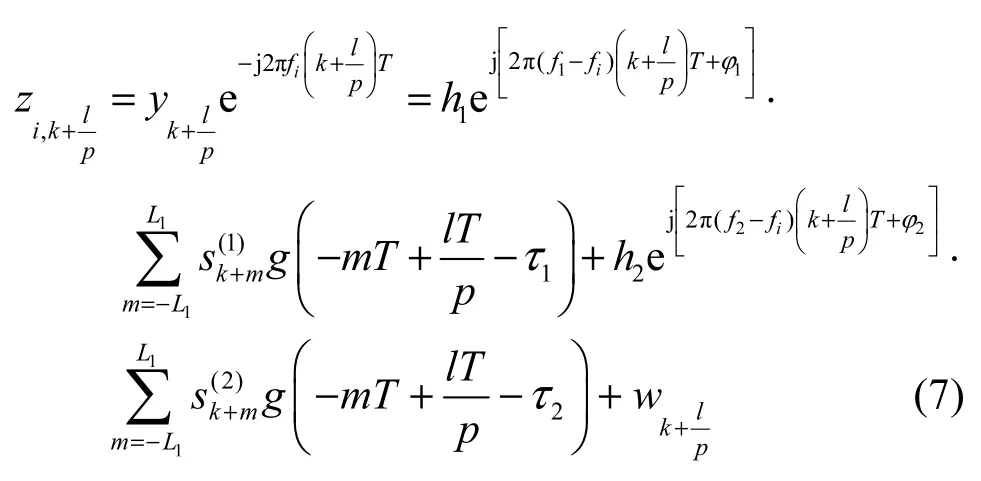
其中，k=t+nN（t=ni,…, ni+K−1; n=0,…, Nf−1），Nf表示数据帧数，

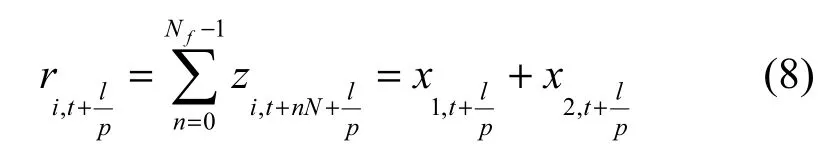
其中

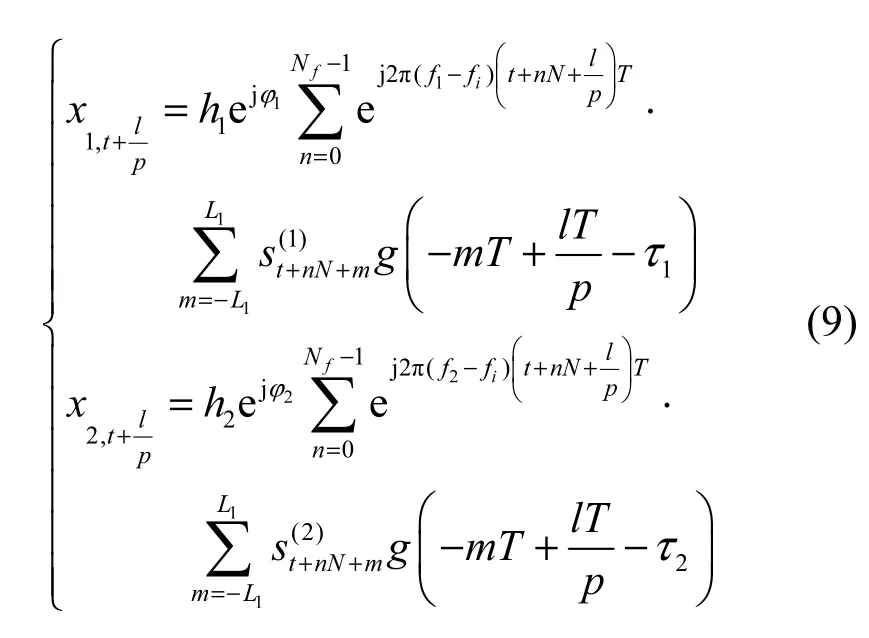
特别地，当i=1时，由于发送数据具有固定的帧长和固定的帧同步符号，加之升余弦脉冲拖尾的衰减系数较大，因此

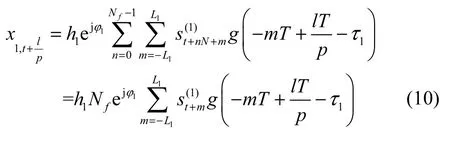
当f1≠f2时，f2−f1的存在会导致第2路信号中符号的相位等概分布于 0～2π区间，且由于同一路信号内的符号之间相互独立，所以当Nf足够大时满足，于是式(8)可化简为

当定时同步不存在误差时，容易得到

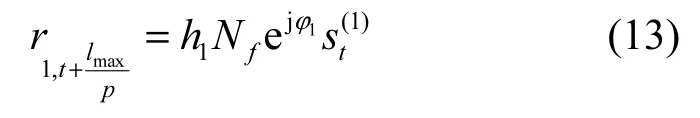
设帧同步符号序列为α0,…,αK−1，则当帧同步符号已知时，第1路源信号的载波初相估计值为

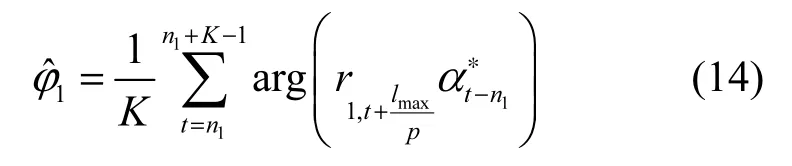
其中，arg(·)表示复数求相位运算。同理，当i=2时，可得到第2路源信号的载波初相估计值为

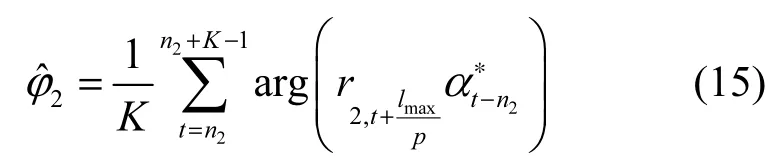
当f1≠f2时，无论2路源信号编码异步还是编码同步，在对第i路进行数据求和后，由于中存在残余频偏，所以当Nf达到某一阈值时必然满足。因此，当2路源信号的频偏不相等时,无论2路源信号编码异步还是编码同步，该方法均有效。

3.3 频偏相等时的初相估计

当2路源信号的频偏相等（设f1=f2=f）时，对p倍过采样的数据进行去频偏操作后，可得

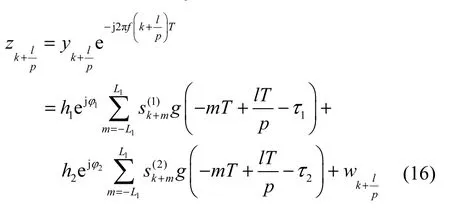
其中，k=t+nN, t=ni,…, ni+K−1; i=1, 2; n=0,…, Nf− 1。在此基础上，当2路源信号编码异步时，通过与式(8)～式(15)相同的过程即可求得 2路源信号的载波初相估计结果。

然而，当2路源信号编码同步（n1=n2）时，对帧同步符号进行数据累加后，结果为

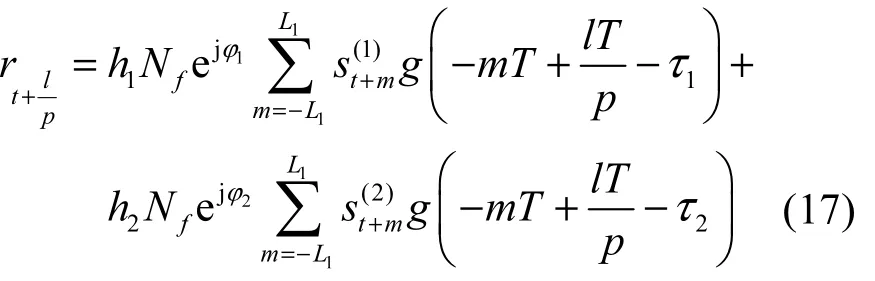
一般情况下，2路信号的最佳定时位置是不同的，所以无法同时实现对2路源信号的最佳采样。然而，当2路信号的最佳定时位置差异较小时，采用最大功率法作定时同步存在的误差也很小，此时在忽略定时偏差影响的条件下，可以实现对2路源信号载波初相的粗估计。

对式(17)做定时同步后，若2路源信号均不存在定时偏差，则可得到

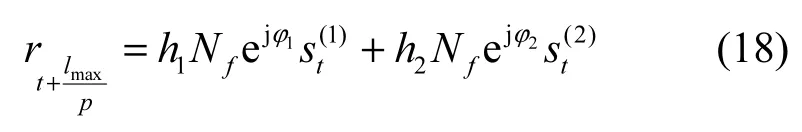
在此基础上，将式(18)与帧同步符号做相关运算，并将结果表示为

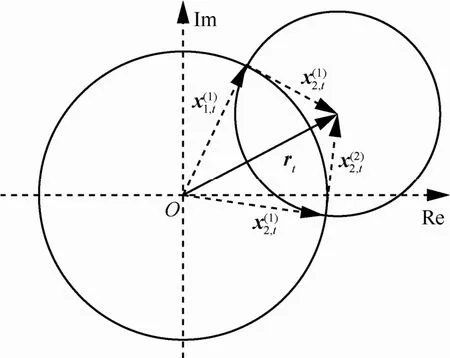
图2频偏相等且编码异步时初相估计的数学模型

当rt≠ 0时，2个圆存在2个交点，此时rt的分解存在2组解。因此，载波初相估计结果存在模糊解，需要借助其他手段去除模糊解。当rt=0时，若A1,t≠A2,t，则2个圆没有交点，载波初相估计无解。若A1,t= A2,t，则2个圆有无穷多个交点，此时载波初相估计具有无穷多解。

4 载波初相估计的MCRB

第3节利用p倍过采样的信号数据完成对载波初相的估计，但并非所有可行的估计方法都针对整数倍采样的信号数据。因此，为了使推导的 MCRB更具通用性，推导过程将采用时间连续的接收信号模型

本文对混合信号的载波初相是逐个独立估计而非联合估计，所以MCRB的推导也针对单一参数估计来进行。若观测区间内的接收信号向量为 y，则对于待估参数φi的任一无偏估计ˆiϕ而言，其估计方差可由比真实CRB略松弛的MCRB来给出。

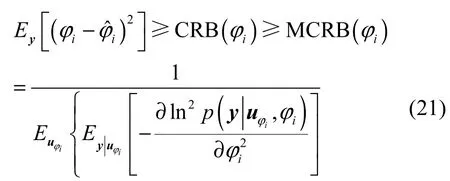
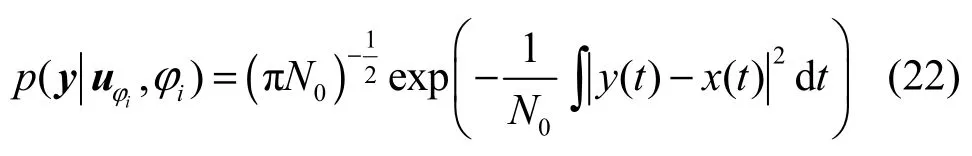
将式(22)代入式(21)，对y求统计平均可通过对噪声项 v(t)求统计平均来代替，则通过对结果进行化简，可得

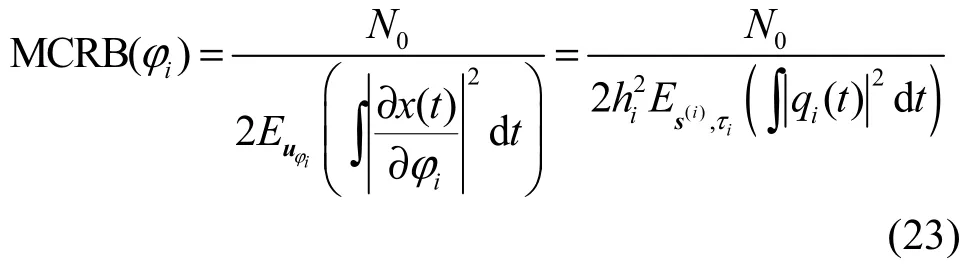
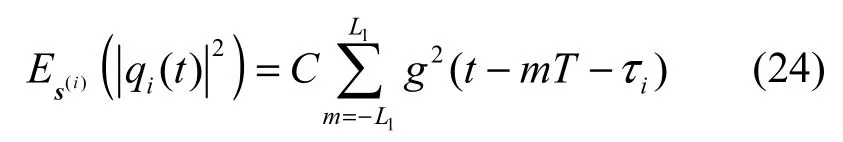
在此基础上，令 L=2L1+1，则式(24)对时间 t求积分可得

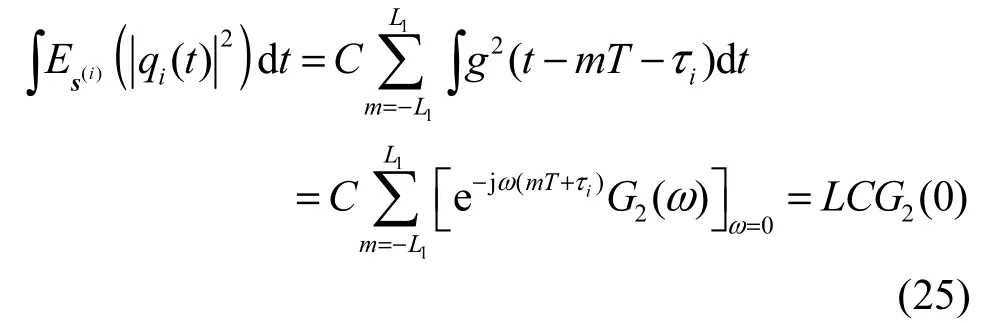
其中，G2()ω为g2(t)的傅里叶变换。将式(25)代入式(23)得

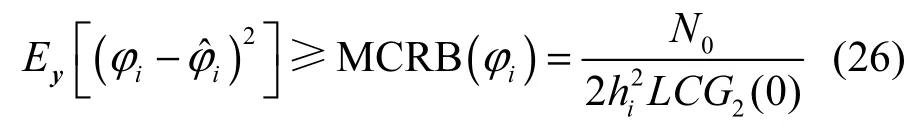
进一步，定义每个混合符号的能量为

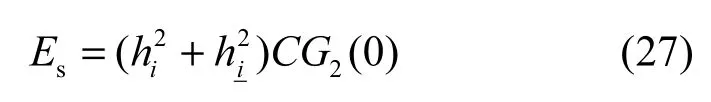
将式(27)代入式(26)，通过化简可得

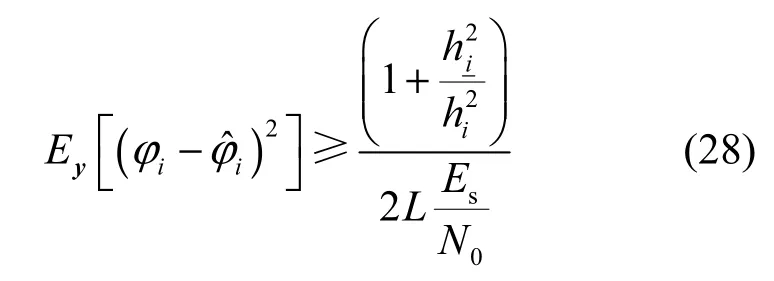
特别地，本文在估计载波初相时仅利用各帧数据中的帧同步符号，不同帧数据的帧同步符号在时间上是不连续的，因此无法直接使用式(28)中的结论。然而，本文的方法可视为用K个连续符号（帧同步符号）做载波初相估计，并对估计的结果做了Nf次平均。因此，估计方差的下界应当为K个连续符号估计方差下界的即

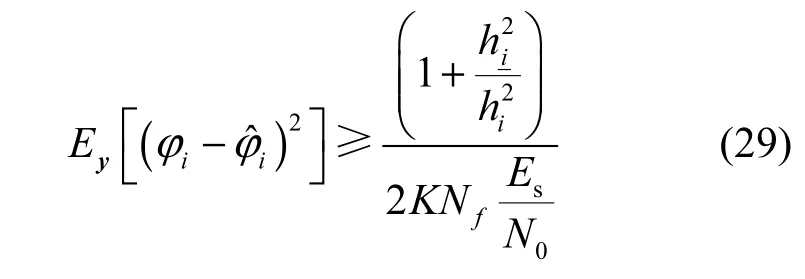
5 仿真分析

考虑2路卫星通信中同调制方式的单通道邻频数字混合信号，符号帧长为N=1600，帧同步符号个数K=10。成型滤波器和匹配滤波器均采用滚降系数为0.3的根升余弦脉冲，过采样倍数p=8。由于实际中2路源信号出现频偏相等且编码同步情况的概率极小，加之频偏相等且编码异步时载波初相的估计方法是一致的，所以仿真中仅考虑2路源信号频偏不同的情况。设置2路信号的幅度分别为h1=1.0、h2=0.8，归一化频偏分别为（T为符号周期），相偏φ1和φ2在[−π, π]内随机产生，时延τ1和τ2在内随机产生。独立重复实验1000次，载波初相的平均估计方差定义为2路源信号估计方差的均值，即。平均MCRB表示2路源信号载波初相估计MCRB的均值。

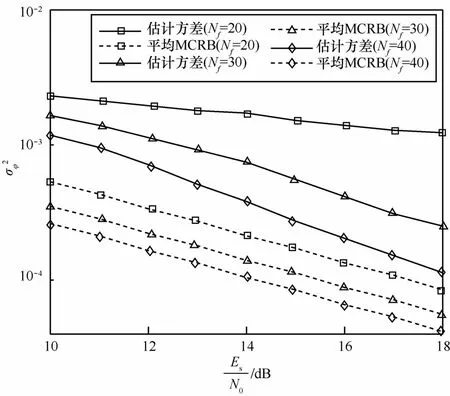
图3初相估计性能与数据帧数间的关系

图4给出了2路邻频QPSK/8PSK/16QAM调制混合信号的初相估计性能曲线。从图中可以看出，本文的方法对3种调制混合信号均适用，但在同样的仿真条件下，随着调制阶数的增加，初相估计性能逐渐变差。原因在于，本文初相估计方法是通过帧累加使第 i路源信号帧同步符号位置的能量增强，而第路源信号则在该位置的能量衰弱。然而，要使第路源信号在第i路源信号帧同步符号位置的能量衰弱到最小，那么在该调制方式下，所有可能的符号必须近似等概率地出现。因此，在同样的累加帧数Nf下，相比调制阶数较低的源信号，调制阶数较高源信号可能的离散符号集合较大，各个可能离散符号等概率出现的可能性降低，所以性能必然下降。此外，从图中可以看出，对于上述3种中估计性能最差的16QAM调制混合信号而言，在给定仿真条件下，估计性能与平均MCRB间约有近1个数量级的性能差距。

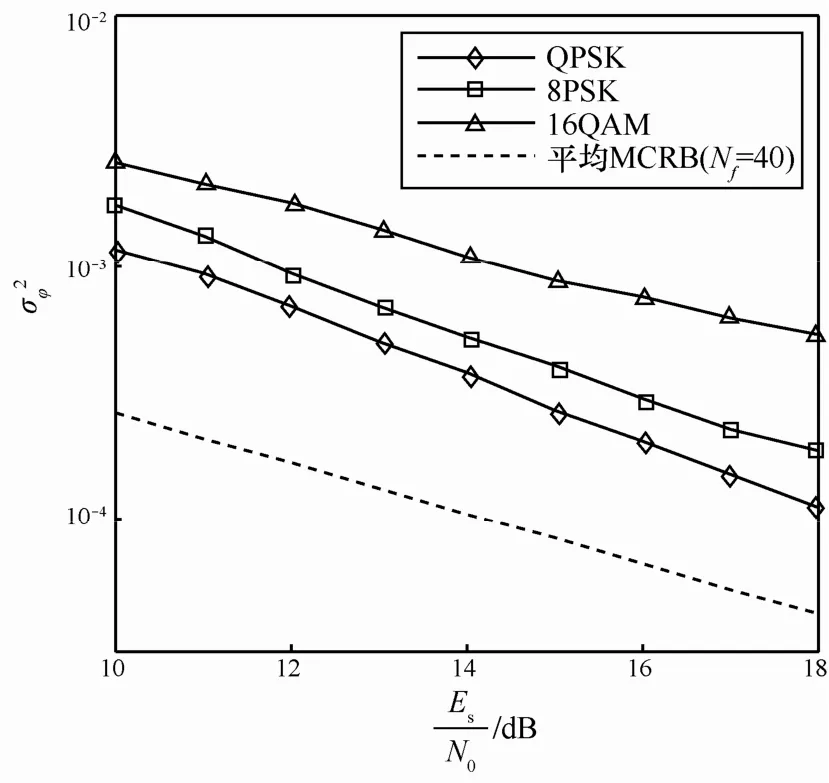
图4不同调制方式下的估计性能

固定h1=1.0，h2在0.1～1.0以0.1为间隔进行变化。在不同幅度比条件下，图5分别给出了2路信号分量的载波初相估计性能和对应的MCRB。从图中可以看出，随着幅度比的增加，φ2的估计方差越来越小，而φ1的估计方差则缓慢增加。原因在于，若较小，那么在估计φ时，2经过Nf帧的累加后，尽管第2路源信号帧同步数据的能量增强，但由于h2较小，所以和大小相当，此时将近似为0将带来较大的误差。此外，从图5中不难发现，在给定仿真条件下，要使弱信号的初相估计方差低于10−2，则幅度比至少达到0.5。

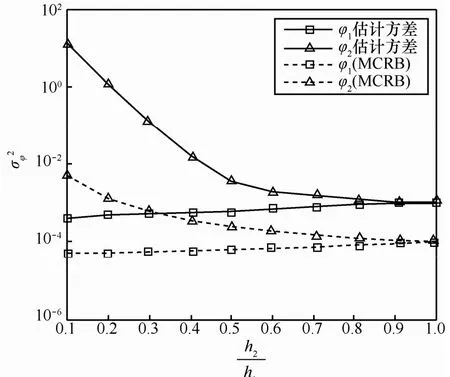
图5不同幅度比下的估计性能（=14 dB，帧数N=40）f

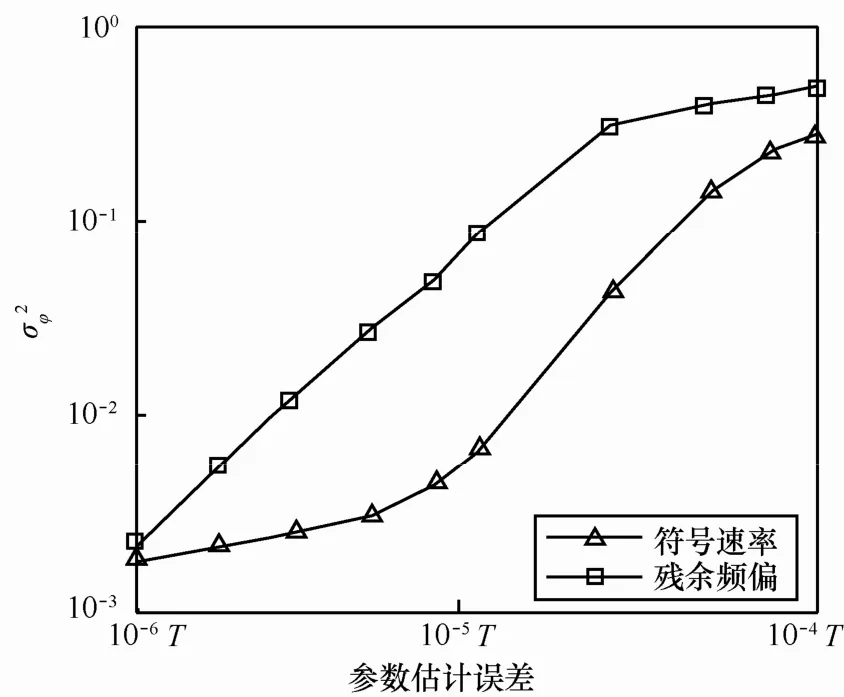
图6存在参数估计误差时的估计性能（=14 dB，帧数N=40）f

基于帧累加方法的初相估计是在残余频偏 fi和符号周期T均估计准确的前提下进行的，然而实际中二者的估计会存在误差，这必将对初相估计结果产生影响。鉴于此，以第1路信号的初相估计性能作为度量，图6分别给出了不同残余频偏估计误差和不同符号速率估计误差条件下的初相估计性能。从图中可以看出，在同样的归一化估计误差下，残余频偏对初相估计的影响大于符号速率。特别地，在上述仿真条件下，要使初相的归一化估计方差低于 10−2，残余频偏估计误差应低于 3×10−6，而符号速率估计误差则低于1.5×10−5。原因可用帧累加过程来解释，不论残余频偏还是符号速率，均以归一化估计误差为1.0×10−5为例。经过 Nf=40帧的累积，频偏估计误差累积的最大相位为 1.28π。由于相位差为 π的同一数据累加结果为零，而上述条件下相邻帧之间累积的相位差为 0.032π，所以帧累加时有近18帧数据同步符号的累加幅度已经抵消。不仅如此，在帧累加过程中，由于每一帧数据因频偏累加的相位不同，所以剩余20多帧帧同步数据累加后将产生额外的相位，从而导致估计结果存在较大的误差。而符号速率估计误差累积的最大时间差为0.64T，不足1个符号周期，所以对初相估计的误差相对较小。实际中，当参数估计误差较大时，通过适当减少累加的帧数也可减小参数估计误差对初相估计性能的影响。

6 结束语

在非合作卫星通信中，针对单通道邻频数字调制混合信号的载波初相估计问题，本文提出一种基于帧累加方法的初相估计算法，并推导出对应的MCRB。仿真结果表明，当帧同步符号累加的帧数达到一定阈值时，该方法可达到接近MCRB的估计性能。此外，在仿真实验中，本文充分考虑了残余频偏和符号速率存在估计误差时对载波初相估计性能的影响，这对实际信号处理具有一定的指导作用。尽管本文的仿真实验仅针对2路同调制方式的QPSK、8PSK和16QAM调制混合信号，但该方案可推广到其他MQAM和APSK等调制混合信号的初相估计，具有较好的工程应用前景。

[1]MARK D. Paired carrier multiple access (PCMA) for satellite communication[C]//Pacific Telecommunications Conference. Honolulu,Hawaii, 1998: 787-791.

[2]GAO B, WOO W L, DLAY S S. Single-channel source separation using EMD-Subband variable regularized sparse features[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2011(4): 961-976.

[3]LU X Y, GAO B, KHOR L C, et al. Single channel source separation using filter bank and 2D sparse matrix factorization[J]. Journal of Signal and Information Processing, 2013(4): 186-196.

[4]朱航, 张淑宁, 赵惠昌. 单通道多分量伪码调制脉冲串信号分离及参数提取[J]. 电子与信息学报, 2015, 37(7): 1702-1709.ZHU H, ZHANG S N, ZHAO H C. Single channel source separation and parameters estimation of multi-component pseudo-random code modulated pulse train[J]. Journal of Electronics amp; Information Technology, 2015, 37(7): 1702-1709.

[5]MEYER R, GERSTACKER W H, SOHOBER R, et al. A single antenna interference cancellation algorithm for increased GSM capacity[J]. IEEE Transactions on Wireless Communications, 2006, 5(4):1-6.

[6]MENG X L, LIU Z, JIANG W L. A single antenna interference cancellation algorithm based on fictitious channels filtering[C]// Proceedings of IEEE 11th International Conference on Signal Processing.Paris, 2012: 179-182.

[7]张立民, 闫文君, 凌青, 等. 一种单接收天线下的空时分组码识别方法[J]. 电子与信息学报, 2015, 37(11): 2621-2627.ZHANG L M, YAN W J, LING Q, et al. A method for blind recognition of space-time block coding using single receive antenna[J]. Journal of Electronics amp; Information Technology, 2015, 37(11):2621-2627.

[8]LIU K, LI H, et al. Single channel blind signal separation of co-frequency MPSK signals[C]//Proceedings of International Conference on Communication, Internet and Information Technology. 2006: 42-46.

[9]TU S L, ZHENG H, et al. Single-channel blind separation of two QPSK signals using per-survivor processing[C]//Proceedings of IEEE Asia Pacific Conference on Circuits and Systems. Macao, China, 2008: 473-476.

[10]杨勇, 张冬玲, 彭华, 等. 利用 Gibbs采样的同频混合信号单通道盲分离[J]. 通信学报，2015, 36(4): 156-162.YANG Y, ZHANG D L, PENG H, et al. Single-channel blind separation of co-frequency modulated signals based on Gibbs sampler[J].Journal on Communications, 36(4): 156-162.

[11]杨勇, 张冬玲, 彭华, 等. 单通道高阶调制线性混合信号的频偏估计[J]. 电子学报, 2015, 43(1): 160-165.YANG Y, ZHANG D L, PENG H, et al. Frequency offset estimation in single-channel linear mixture of high-order modulated signals[J]. Acta Electronica Sinica, 2015, 43(1): 160-165.

[12]万坚, 涂世龙, 廖灿辉, 等. 通信混合信号盲分离理论与技术[M].北京: 国防工业出版社, 2012: 221-224.WAN J, TU S L, LIAO C H, et al. Theory technology on blind source separation of communication signals[M]. Beijing: National Defense Industry Press, 2012: 221-224.

[13]廖灿辉, 周世东, 朱中梁. 基于最大似然的同频混合信号联合定时估计算法[J]. 系统工程与电子技术, 2010, 32(6): 1121-1124.LIAO C H, ZHOU S D, ZHU Z L. ML-based joint timing estimation algorithm for co-frequency signals[J]. Journal of Systems Engineering and Electronics, 2010, 32(6): 1121-1124.

[14]涂世龙, 郑辉. 单通道同频线性调制混合信号的时延估计[J]. 数据采集与处理, 2010, 25(4): 449-453.TU S L, ZHENG H. Time delay estimation of co-frequency linear modulated signals using single-channel mixture[J]. Journal of Data Acquisition amp; Processing, 2010, 25(4): 449-453.

[15]郭一鸣, 杨勇, 张冬玲, 等. 单通道同频混合信号时延高效估计方法[J]. 系统工程与电子技术, 2014, 36(7): 1416-1421.GUO Y M, YANG Y, ZHANG D L, et al. Efficient time delay estimation algorithm for single-channel co-frequency signals[J]. Journal of Systems Engineering and Electronics, 2014, 36(7): 1416-1421.

[16]潘申富, 李峰, 李文铎, 等. PCMA 系统中干扰信号的载波相位估计[J]. 电子对抗, 2004, (6): 8-11.PAN S F, LI F, LI W D, et al. Interference carrier phase estimation in PCMA system[J]. Electronic Warfare, 2004, (6): 8-11.

Carrier initial phases estimation for single-channel adjacent-frequency mixture of digitally modulated signals

YANG Yong1, GUO Yi-ming1, WANG Hai-xin2, PENG Hua1, ZHANG Dong-ling1
(1. School of Information Systems Engineering, PLA Information Engineering University, Zhengzhou 450002, China;2. Southwest Electronics and Telecommunication Technology Research Institute, Chengdu 610041, China)

For single-channel mixture of adjacent-frequency digitally modulated signals which have the fixed frame length and sync codes in non-cooperative satellite communications, a carrier initial phases estimation algorithm which can be applied to both low-order and high-order digitally modulated mixtures was provided according to the differences of parameters in the source signals. The sync data eliminated the frequency offset was added in the interval of frame length firstly, then timing synchronization was accomplished for the added result in terms of power maximization rule,thus the initial phases information was derived. Moreover, the modified Cramer-Rao bound (MCRB) of carrier initial phases for single-channel mixture of adjacent-frequency digitally modulated signals was derived for comparison. Simulation results show that, difference between estimation performance of the proposed algorithm and MCRB becomes smaller with the increase in the number of added frames.

single-channel mixture, adjacent-frequency interference, carrier initial phases estimation, modified Cramer-Rao bound

The National Natural Science Foundation of China (No.61401511)

TN911.7

10.11959/j.issn.1000-436x.2016205

2016-05-05；

2016-08-25

国家自然科学基金资助项目（No.61401511）