三维矩形布局吸引子性质的研究

王金敏

(天津职业技术师范大学，天津 300222)

三维矩形布局吸引子性质的研究

王金敏

(天津职业技术师范大学，天津 300222)

吸引子法作为一种量化的定位规则，在解决三维布局问题时取得了较好的效果。对解决三维矩形布局问题的吸引子法进行了研究，获得了吸引子法的一些基本性质，如最佳布入点、吸引子法的趋角性、隐性吸引子的“唯一”性以及位置的“动态性”等，有利于吸引子法在三维矩形布局求解中得到更好地运用。

矩形布局；启发式算法；吸引子法；定位规则；定位函数

三维矩形布局问题[1-2]广泛存在于现代生产及生活中，如集装箱内货物箱子的摆放、仪器舱内各种仪器的布局、生产车间内设备的布置等。布局问题已被证明为NP难问题。三维矩形布局问题的求解算法[3]，主要有优化算法和启发式算法。优化算法只能解决小规模问题，并且解的质量往往依赖于初始解的选择。启发式算法[4-5]是基于直观或经验构造的算法，其在可接受的计算时间和空间内给出待解决问题的一个可行满意解。

近些年来，随着启发式算法种类的增多和研究者对前人布局智慧的总结，在布局问题的研究领域出现了许多新型启发式算法。如 Zhang等[6]采用分层思想，分别利用深度和广度优先搜索方法来解决布局问题；Wei等[7]基于三维矩形布局的极限点提出了块构建启发方法，并融合到一个使用迭代构建策略的树搜索算法中；Cui等[8]利用不同模式的组合提出一种基于序列值的启发式算法解决二维切割问题。

布局构造启发算法是最常见的一种启发式算法。构造算法主要由定序规则和定位规则所决定。确定量化的定序规则和定位规则即建立相关的定序函数和定位函数，可以将不同的布局算法综合统一。吸引子法[9]是定位函数中的一种。吸引子法吸收了下台阶法、BL算法等许多定位规则的优点，并且其可量化的特点使其易于计算。吸引子法利用定位函数中参数的不同取值可以获得不同的布局求解算法；如果参数选择得当，则可得到较佳的求解算法。

以前的文献多数注重对于吸引子法的应用，如王金敏等[10]利用蜜蜂进化型遗传算法优化吸引子函数中的参数来求解三维矩形布局问题。而对吸引子法性质的研究仅有文献[11]对二维矩形布局的情况进行了论述。

本文对解决三维矩形布局问题的吸引子法进行研究，得出了吸引子法的一些基本性质，利于吸引子法在三维矩形布局问题求解中得到更好地运用。

1 三维矩形布局问题

三维矩形布局问题是指将若干个尺寸不同或者相同的长方体(或正方体)布局块，放置在一个长方体(或正方体)的布局空间内，要求布局空间的利用率尽可能大，且满足：

(1) 布局块完全放置在布局空间内；

(2) 布局块之间不能发生干涉；

(3) 布局块的表面分别与布局空间表面平行或垂直。

2 吸引子法简介

在布局空间内设置k个吸引子，其中吸引子t的坐标为(xt, yt, zt)，则布局块b在(x, y, z)处的定位函数为：

其中，tω为吸引子参数，且为权重因子，且αt+βt+γt= 1；ωt、αt、βt、γt∈[0,1]。

在布局时吸引子t吸引布局物体向其移动或靠近，从而达到布局定位的效果。吸引子布局可分为静态和动态 2种方式。静态方式是指定位函数的各个权重因子数值(强度)和吸引子位置在布局过程中始终保持不变；动态方式是指吸引子位置在布局过程中随着布局条件而变化，或吸引子位置不变但权重因子数值发生变化。本文主要对静态方式进行研究。

3 吸引子性质

本文研究定位函数中参数αt、tβ、γt和ωt确定情况下，定位函数的变化情况。不失一般性，令布局块的布入参考点为其几何中心。现将吸引子分别放在布局空间的 8个角点，并令布局空间的尺寸为L×W×H，如图1所示。

图1 布局空间及吸引子分布

布局块b在(x, y, z)处的定位函数为：

整理得：

其中，

根据吸引子法的定义，布局块 b在布局空间的最佳布入点(x, y, z)应满足：

其中，(x,y,z)∈I，I为布局可行域。

当αt、βt、γt和ωt确定时，A、B、C和D为常数，根据吸引子定位函数的定义有 G(x,y,z)≥0，因此，理论上有Min G(x,y,z)= 0，即：

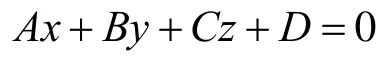
也就是最佳布入点应在一平面上。又由于布入点(x, y, z)应处在布局可行域内，因此布局块 b在布局空间的最佳布入点(x, y, z)处在法向为(A, B, C)的平面上。由此得以下性质：

性质1. 在三维矩形布局空间内，定位函数值相同的点在同一个平面上，该平面的法矢量为(A, B, C)。

由于布入点(x, y, z)应处在布局可行域内，又处在法向为(A, B, C)的平面族上，因此，最佳布入点一定在布局可行域的边界上即可行域顶点上。显然，顶点可分为凸点和凹点。不妨令p1(x, y, z)为定位函数值最小的凹点，且布局可行域边界上与P1相邻的凸点为p(x+Δx,y+Δy,z+Δz )，则：

下面根据 A、B、C的不同取值分别讨论当G(x+Δx,y+Δy,z+Δz)≤G(x,y,z)时，凸点p是否存在的情况。

(1)A≥0,B≥0,C≥0。此时在布局可行域边界上一定存在凸点p，使Δx≤0,Δy≤0,Δz≤0成立。此时最佳布入点应为左、前、下的凸点即图1 中1点方位。

(2)A≥0,B≥0,C≤0。此时存在凸点p，使Δx≤0,Δy ≤0,Δz≥0成立；因此，最佳布入点应为左、前、上的凸点即图1中5点方位。

(3)A≥0,B≤0,C≥0。存在凸点p，使Δx≤0,Δy≥0,Δz≤0；最佳布入点应为左、后、下的凸点即图1中4点方位。

(4)A≥0,B≤0,C≤0。存在凸点p，使Δx≤0,Δy≥0,Δz≥0；最佳布入点应为左、后、上的凸点即图1中8点方位。

(5)A≤0,B≥0,C≥0。存在凸点p，使Δx≥0,Δy≥0,Δz≤0；最佳布入点应为右、前、下的凸点即图1中2点方位。

(6)A≤0,B≥0,C≤0。存在凸点p，使Δx≥0,Δy≤0,Δz≥0；最佳布入点应为右、前、上的凸点即图1中6点方位。

(7)A≤0,B≤0,C≥0。存在凸点p，使Δx≥0,Δy≥0,Δz≤0；最佳布入点应为右、后、下的凸点即图1中3点方位。

(8)A≤0,B≤0,C≤0。存在凸点p，使Δx≥0,Δy≥0,Δz≥0；最佳布入点应为右、后、上的凸点即图1中7点方位。

性质2. 最佳布入点一定为布局可行域中的凸点。

根据性质 2可知，当利用吸引子法作为定位函数进行三维布局时，布局块会趋向堆积在布局空间的一个“角点”上，根据A、B和C取值的不同，堆积的角点不同，堆积的状态不同。这就是吸引子法的趋角性。

布局空间只是整体空间的一部分，布局块只能放置于布局空间内，在整体空间内任意放置若干吸引子，且放置位置不受布局空间限制的情况如下：

令布局块b在布入点(x, y, z)对位于(xt, yt, zt)的吸引子t的定位函数为：

其中，当 x≥xt时，lt=1；否则，lt=-1。当 y≥yt时， mt=1；否则， mt=-1。当 z≥zt时， nt= 1；z＜zt时， nt=-1。

因此，布局块b在布入点(x, y, z)对位于(xt, yt, zt)的吸引子t的定位函数为：

整理得：

其中，

当参数ωt、αt、βt、γt为定值，吸引子个数k和位置(xt, yt, zt)确定时，参数lt、mt、nt也为定值，则A、B、C、D为定值。如果A=B=C=0，此时G(x, y, z)=D，即定位函数为定值，吸引子不产生“效果”。因此，使用吸引子法布局时，应避免此种情况。对这种情况，可认为任意一点皆可为吸引子。当参数A、B和C中有一个不为零时，不失一般性令A不为零，可得 G(x,y,z) = A(x + D/A) +By+Cz+D 。由此可知无论使用多少个吸引子，吸引子如何布置，参数大小如何，布局块b在布入点(x, y, z)的定位函数都相当于在空间内设置了“一个”吸引子的定位函数。

性质3. 当布入点在某一空间内，无论使用多少个吸引子，吸引子如何布置，参数大小如何设定，其达到的定位效果都相当于对此空间设置了一个“隐性”吸引子的效果。

通常，k个吸引子可将整体空间划分为(k+1)3个子空间，图2所示为1个吸引子划分子空间的情况。在每个子空间性质3均成立。

图2 1个吸引子划分空间的情况

性质4. 在整体空间内，“隐性”吸引子的位置既与所设吸引子数量和位置有关，也与布入点相对吸引子的位置有关。

当吸引子布置在布局空间边界上或外部时，“隐性”吸引子则可能在布局空间的角点、边界线或边界上，这时布局块会受到该吸引子的吸引而产生趋角、贴面的效果，如图3所示。

图3 吸引子布置在布局空间边界上

当吸引子布置在布局空间内时，“隐性”吸引子也在布局空间内部，这时布局块会受到吸引而趋向该吸引子，如图4所示。

图4 吸引子布置在布局空间内

4 结 论

目前在布局研究领域出现了许多新型启发式算法；吸引子法也为其中一种。吸引子法吸收了下台阶法、BL算法等许多定位规则的优点，其通过确定优化定位函数，来获得满意的布局结果。

本文通过分析推导，得出了三维布局吸引子法的一些基本性质，揭示了吸引子的趋角性及“隐性”吸引子的动态性，利于更好地应用吸引子法解决布局问题。

[1] Dyckhoff H. A typology of cutting and packing problems [J]. European Journal of Operational Research, 1990, 44(2): 145-159.

[2] Wascher G, HauBner H, Schumann H. An improved typology of cutting and packing problems [J]. European Journal of Operational Research, 2007, 183(3): 1109-1130.

[3] Cagan J, Shinada K, Yin S. A survey of computational approaches to three-dimensional layout problems [J]. Computer-Aided Design, 2002, 34(8): 597-611.

[4] Egeblad J, Pisinger D. Heuristic approaches for the twoand three-dimensional knapsack packing problem [J]. Computer & Operations Research, 2009, 36(4): 1026-1049.

[5] Burke E K, Hyde M, Kendall G, et al. A genetic programming hyper-heuristic approach for evolving 2-D strip packing heuristics [J]. IEEE Transaction on Evolutionary Computation, 2010, 14(6): 1-17.

[6] Zhang D F, Yu P, Leung S C H. A heuristic block-loading algorithm based on multi-layer search for the container loading problem [J]. Computers & Operations Research, 2012, 39(10): 2267-2276.

[7] Wei L J, Oon W C, Zhu W B, et al. A reference length approach for the 3D strip packing problem [J]. European Journal of Operational Research, 2012, 220(1): 37-47.

[8] Cui Y P , Cui Y D, Tang T B. Sequential heuristic for the two-dimensional bin-packing problem [J]. European Journal of Operational Research, 2015, 240(1): 43-53.

[9] 王金敏, 杨维嘉. 动态吸引子在布局求解中的应用[J].计算机辅助设计与图形学学报, 2005, 17(8): 1725-1729.

[10] 王金敏, 朱丽萍, 甄士刚. 一种基于蜜蜂进化选择算子的布局遗传算法[J]. 图学学报, 2014, 35(5): 690-696.

[11] 王金敏, 齐 杨. 矩形布局问题吸引子法研究[J]. 图学学报, 2012, 33(6): 38-44.

Research on the Property of Attractive Factor in Three Dimensional Rectangular Packing Problem s

Wang Jinm in

(Tianjin University of Technology and Education, Tianjin 300222, China)

The attractive factor approach, which is one of the quantitative positioning rules, has got satisfactory effects in solving three-dimensional packing problems. The paper studies the attractive factor approach and gets some properties as follows: best fit packing point, taxis to convex and corner point, uniqueness of invisible attractor factor and the “dynam ic” of location. It w ill be conducive to enable the better usage of attractor factor approach in solving three-dimensional rectangular packing problems.

rectangular packing problems; heuristic algorithm; attractor factor approach; positioning rule; positioning function

TP 391

10.11996/JG.j.2095-302X.2016030355

A

2095-302X(2016)03-0355-04

2015-11-28；定稿日期：2015-12-20

国家自然科学基金项目(60975046)；天津职业技术师范大学科研发展基金项目(KJ14-64)

王金敏(1963–)，男，河南舞阳人，教授，博士。主要研究方向为智能布局、计算机辅助设计及图形学。E-mail：wang_jin_m in@163.com